矢量泵喷推进潜航器回转性能研究

韩 伟，邓 倪

（1.兰州理工大学能源与动力工程学院，兰州 730050；2.甘肃省流体机械重点实验室，兰州 730050）

0 引 言

随着船舶动力系统的不断更新以及船舶回转性能、安全性能需求的提高，矢量泵喷推进器逐渐成为国内外学者研究的重点。即使通过设计不同形式的船舵也很难解决在低航速下其控制效率大幅降低的问题，而矢量泵喷推进器能够有效地解决传统船舵控制在低航速下控制效率低的问题[1]。

目前，国内外学者对于矢量泵喷潜航器回转性能的研究主要针对矢量。Mohseni[2]提出了一种新的水下机器人低速机动机制，采用紧凑的脉动射流执行器实现低速机动能力；Geng 等[3]通过双合成射流执行器的同相工作实现水下航行器的横向运动，通过这两个执行器的异相工作实现偏航运动；Chocron 等[4]采用多个推进器组成推力配置矩阵，以合成合适的推进系统；Cavallo 等[5]研究了一种新概念、配备三自由度矢量推进器的自动水下航行器；Kaya等[6]采用不同方向的固定推进器实现预定轨迹的航行；Nawrot[7]探讨了许多推力矢量装置的替代设计策略和概念；Liu 等[8]提出了一种带有矢量推力导管推进器的鱼雷形状水下机器人，并设计了矢量推进器的控制方案，实现了在零速或慢速前进速度下完成任务；陈路伟等[1]提出一种采用可动矢量喷管的喷水推进式水下航行器，可以有效提高机动性；高富东等[9]提出采用多矢量水下推进航行器，通过调整推进器的偏转方向实现对航行器的姿态控制；高双[10]建立了推力矢量船舶运动的仿真模型，获得喷角的改变对船舶纵向推力损失和转向力矩损失的影响规律，为了保证船舶启动过程的安全运行，对船舶转弯过程中的横倾角度加以控制，以获得此状态时的喷管转动角度；曾薄文[11]利用MMG 分离原理建立了喷水推进无人艇的操纵运动方程，在矢量喷管转动的过程中，喷流偏转使得纵向力、转向力矩和速度发生变化，基于开环运动模型，总结出了喷管偏转对潜艇航行速度损失的影响规律。综合矢量推进器以及舵的优点，同时使用舵以及矢量喷管转向，能够在较小舵角及喷管偏角的条件下实现较大角度的转向，进一步提高潜航器机动性。多套控制系统的存在也可以避免单套控制系统失效情况下潜航器失控。

为了改善潜航器的回转性能，本文在传统船舵控制的基础上结合矢量推进器控制，通过对潜航器回转运动进行仿真，分析不同控制模式下的回转性能，以验证矢量推进器对潜航器回转性能的影响，以期为潜航器应用矢量推进器的研究提供一定的参考。

1 潜航器水平面运动数学模型

潜航器在水下的操纵运动，在一般情况下可以视为刚体在流体中的空间运动[12]。潜航器在水中运动所受到外力大致上可以分为流体动力和非流体动力两大类。本文研究潜航器在水中做水平面运动时通过不同控制装置的操纵运动，建立水平面运动模型并进行仿真。

1.1 水平面操纵运动的一般方程

本文采用国际拖曳水池会议（International Towing Tank Conference，简称为ITTC）推荐的和造船与轮机工程学会（SNAME）术语公报[13]的体系，包括两个右手系，如图1 所示：一个为原点固定在地球上的固定坐标系E-ξη；另一个为原点固定在潜航器上，随潜航器共同运动的运动坐标系G-xy。

图1 矢量泵喷推进潜航器水平面运动坐标系Fig.1 Horizontal motion coordinate system of vector pump jet propulsion submersible

根据质心运动定理以及相对于质心运动的动量定理、动量矩定理，推导出潜航器水平面操纵运动的一般方程：

式中，m为潜航器质量，u、v分别为潜航器重心G的航速在x、y方向上的分量，u̇、v̇为对应的加速度，r为角速度，Iz为潜航器对随体坐标系Gz轴的转动惯量，X、Y分别为潜航器所受外力在x、y方向上的分量，N为外力对重心G的力矩。

1.2 作用于潜航器的力与力矩

在潜航器做水平面运动时，潜航器所受到的非流体动力，如浮力、重力等，可以不作考虑，因此，本文只考虑潜航器在水中所受到的流体动力。

本文所研究的对象为艇体-舵-矢量泵喷推进器所组成的大系统，假设潜航器在水下处于无限深广、静水的环境中，此时，潜航器所受到的流体动力只取决于潜航器自身的运动状态，表示为函数形式：

式中，F(X,Y,N)为潜航器所受外力与力矩，δr、δ̇r分别为船舵的转动角以及转舵速度，δn、δ̇n分别为矢量喷管的偏转角以及转动速度，n为泵喷推进器的转速。

一般情况下，对泵喷推进器所产生的推力做单独处理，记为FT(XT,YT)和NT，如图2所示：

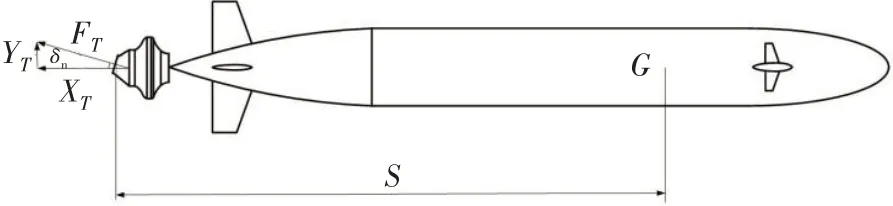
图2 矢量泵喷推进器的推力分解示意图Fig.2 Schematic diagram of thrust of vector pump jet propeller

式中，S为喷管出口中心到潜航器重心的距离。

本文采用矢量螺旋混流式泵喷推进器，由螺旋混流式泵以及矢量喷管组成，按比例缩小后的模型泵设计参数如表1所示。

表1 螺旋混流泵设计参数Tab.1 Design parameters of screw mixed flow pump

矢量泵喷推进器依靠叶轮对水流进行加速增压，水流通过喷管向后喷射加速对潜航器产生反作用力，即泵喷推进器产生的推力FT，推力的大小等于单位时间上进出推进器的水流的动量差：

式中，Qm为流经泵喷推进器的质量流量，Vj、Vs分别为矢量泵喷推进器进出口流速。

本文采用的矢量喷管为收缩喷管，喷管收缩比为κ，根据连续方程可得喷管进出口速度比为

根据式（4）和式（5），结合螺旋混流泵的水力参数、无量纲参数，可推导出推力与转速的函数关系如下[14]：

式中，N0为设计轴功率，η0为设计水力效率，ϕ为流量的无量纲参数，b2为叶轮出口宽度，ψ为扬程的无量纲参数，Aj、As分别为矢量泵喷推进器进出口面积。

根据式（6）～（7）可以通过相似理论由模型泵推力系数C计算出对应的实际尺寸的泵喷推进器推力系数。

忽略船舵和矢量喷管的转动速度，将F投影到运动系坐标轴上，表示为函数形式：

根据多元函数的泰勒级数展开原理，以潜航器做等速直航的平衡状态，即u0≠0、v0=r0=u̇0=v̇0=ṙ0=δr0=0为基准运动，忽略二阶以上高阶项的影响，对其进行泰勒级数展开：

式中，X0、Xu、…、Xuu、…都是水动力分量对潜航器运动参数的偏导数在展开点的值，统称为水动力系数。

1.3 水平面操纵运动方程

考虑到潜航器的左右对称性，忽略比较小的水动力系数，同时，为了书写方便，将二阶项的系数1/2!并入对应的水动力系数中，于是得到水平面操纵运动非线性方程：

1.4 水平面操纵运动重心轨迹方程

根据式（12），在潜航器质量、喷管出口中心到潜航器重心的距离、潜航器对随体坐标系Gz轴的转动惯量和各项水动力系数已知的情况下，给定潜航器操纵规律δr(t)、δn(t)，可以求出潜航器的各项运动参数u(t)、v(t)、r(t)，记潜航器的首向角为φ，则φ̇(t)=r(t)，结合这些运动参数可以求出潜航器的重心轨迹方程：

2 仿真实验

本文所使用的潜航器模型出自文献[15]，采用的矢量泵喷推进器则是基于课题组所设计的螺旋混流式矢量泵喷推进器，通过对不同操纵机制，即船-舵-推进器、船-矢量推进器和船-舵-矢量推进器三种不同的潜航器控制方法进行仿真对比，分析潜航器的最佳操纵模式。

2.1 低航速下的潜航器回转性能

为了对比低航速下潜航器做回转运动时三种控制方法的回转性能，本文设置初始航速为1 m/s，设置舵的偏角、矢量喷管的偏角如表2 所示，仿真结果如图3所示。

表2 三种控制方法下的参数设置Tab.2 Parameter setting under three control modes

图3 三种控制方式的仿真结果Fig.3 Simulation results of three control modes

图3显示了低航速下船-矢量推进器、船-舵-推进器和船-舵-矢量推进器三种不同的控制方法时潜航器做回转运动的仿真结果。由图3（a）潜航器的运动轨迹可以看出，船-矢量推进器系统的回转半径约为131 m，船-舵-推进器系统的回转半径约为201 m，船-舵-矢量推进器系统的回转半径约为102 m，使用矢量推进器可以有效地减小潜航器的回转半径，船-舵-矢量推进器系统的回转半径最小。由图3（b）潜航器的轴向速度可以看出，大角度的矢量喷管偏角对潜航器的轴向速度影响较大，这与推力矢量的偏转导致轴向推力下降有关。由图3（c）潜航器的横向速度可以看出：船-舵-推进器系统的横向速度的稳定值最小，为0.164 m/s；而船-矢量推进器系统的横向速度与船-舵-矢量推进器系统的横向速度的稳定值几乎相等，为0.220 m/s。由图3（d）潜航器的偏航角速度可以看出：船-舵-推进器系统的偏航角速度最小，为0.175°/s；船-矢量推进器系统的偏航角速度最大，为0.272°/s；而船-舵-矢量推进器系统的偏航角速度为0.248°/s。由图3（e）潜航器的偏航角可以看出：船-舵-推进器系统的偏航角最小，为197.670 °，潜航器偏航180°需要896 s；船-舵-矢量推进器系统的偏航角最大，为279.030 °/s，潜航器偏航180°需要601 s；而船-矢量推进器系统的偏航角为275.593 °/s，潜航器偏航180°需要647 s。使用矢量推进器可以有效加快低航速下潜航器的偏航速度，使得低航速下潜航器掉头时间缩短4～5 min。

2.2 推进器设计转速下的潜航器回转性能

本节设置泵喷推进器转速为1500 r/min，初始航速为10 m/s，设置舵的偏角分别为0°、5°、10°、15°、20°、25°、30°、35°、40°，矢量喷管的偏角分别为0°、5°、10°、15°、20°、25°、30°、35°、40°，除直航运动条件，即舵与矢量喷管偏角均为0°外，对共80种组合进行仿真，仿真结果如图4所示。

图4 设计转速下回转运动特征参数Fig.4 Characteristic parameters of rotary motion at design speed

图4表示推进器在设计转速下不同舵角、矢量喷管偏角时潜航器做回转运动的仿真结果。由图4（a）潜航器的回转半径可以看出，船-舵-推进器系统的回转半径在舵角小于33°时小于船-矢量推进器系统对应喷管偏角时的回转半径，但当舵角大于33°后，船-矢量推进器系统对应的回转半径更小，这与矢量推进器提供的转矩变化率随喷管偏角的增大而增大相关，而船-舵-矢量推进器系统的回转半径最小，这也表明了使用矢量泵喷推进器可以有效减小潜航器的回转半径。由图4（b）潜航器的回转周期可以看出，船-舵-推进器系统的回转周期在舵角小于23°时小于船-矢量推进器系统对应喷管偏角时的回转周期，另一方面，当舵角达到30°后继续增大舵角，潜航器的回转周期几乎不变，而增大喷管偏角则可以减小回转周期。由图4（c）、图4（d）潜航器的纵距、正横距可以看出，在小舵角（喷管偏角）情况下，船-舵-推进器系统的纵距、正横距小于船-矢量推进器系统对应喷管偏角时的纵距、正横距，但在大舵角（喷管偏角）情况下，船-矢量推进器系统对应的纵距、正横距更小，而船-舵-矢量推进器系统的纵距、正横距最小。由图4（e）潜航器的战术直径可以看出，在小舵角（喷管偏角）情况下，船-舵-推进器系统的战术直径小于船-矢量推进器系统对应喷管偏角时的战术直径，但在大舵角（喷管偏角）情况下，船-矢量推进器系统对应的战术直径更小，而船-舵-矢量推进器系统的战术直径最小。总的来说，矢量推进器的运用可以改进潜航器的回转性能，船-舵-矢量推进器系统的回转性能为最佳。

通过对图4中数据进行非线性拟合，采用rational2D 拟合方法，建立回转半径Rs、回转周期T、纵距La、正横距Ld、战术直径DT随舵角δr、喷管偏角δn变化的数学模型:

2.3 控制轴向航速下的潜航器回转性能

本节设置初始航速为10 m/s，控制轴向航速为10 m/s，设置舵的偏角分别为0°、5°、10°、15°、20°、25°、30°、35°、40°，矢量喷管的偏角分别为0°、5°、10°、15°、20°、25°、30°、35°、40°，除直航运动条件，即舵与矢量喷管偏角均为0°外，对共80种组合进行仿真，仿真结果如图5所示。

图5 控制轴向航速下回转运动特征参数Fig.5 Characteristic parameters of rotary motion at controlled axial speed

图5 表示在控制轴向航速为10 m/s 下不同舵角、矢量喷管偏角时潜航器做回转运动的仿真结果。由图5（a）潜航器的回转半径与图4（a）对比可以看出，控制轴向航速（此时泵喷推进器的转速由轴向航速控制器调节）时的回转半径与保持泵喷推进器的转速（此时潜航器有轴向航速损失）时的回转半径几乎相同，可见舵角、矢量喷管偏角的大小才是决定潜航器回转半径的关键因素，运动参数与泵喷推进器转速的不同对回转半径的影响很小。由图5（b）潜航器的回转周期可以看出，船-舵-推进器系统的回转周期在舵角小于37°时小于船-矢量推进器系统对应喷管偏角时的回转周期，而增大舵角或喷管偏角均可以减小回转周期，与图4（b）对比可以看出，在小舵角（喷管偏角）情况下，控制轴向航速会增大回转周期，但在大舵角（喷管偏角）情况下，特别对于船-舵-矢量推进器系统来说，可以大幅度减小潜航器的回转周期。由图5（c）潜航器的纵距可以看出，船-舵-推进器系统的纵距小于船-矢量推进器系统对应喷管偏角时的纵距，而船-舵-矢量推进器系统的纵距最小，与图4（c）对比可以看出，对于船-舵-推进器系统，控制轴向航速可以减小纵距；对于船-矢量推进器系统，在小喷管偏角情况下，控制轴向航速可以减小纵距，但在大喷管偏角情况下，控制轴向航速会增大纵距；对于船-舵-矢量推进器系统，在大舵角、小喷管偏角情况下，控制轴向航速可以减小纵距，但在小舵角、大喷管偏角情况下，控制轴向航速会增大纵距。由图5（d）潜航器的正横距可以看出，在小舵角（喷管偏角）情况下，船-舵-推进器系统的正横距小于船-矢量推进器系统对应喷管偏角时的正横距，但在大舵角（喷管偏角）情况下，船-矢量推进器系统对应的正横距更小，而船-舵-矢量推进器系统的正横距最小，与图4（d）对比可以看出，对于船-舵-推进器系统，控制轴向航速可以减小正横距；对于船-矢量推进器系统，在小喷管偏角情况下，控制轴向航速会增大正横距，但在大喷管偏角情况下，控制轴向航速可以减小正横距；对于船-舵-矢量推进器系统，在大舵角、大喷管偏角情况下，控制轴向航速可以减小正横距，但在小舵角、小喷管偏角情况下，控制轴向航速会增大正横距。由图5（e）潜航器的战术直径可以看出，在小舵角（喷管偏角）情况下，船-舵-推进器系统的战术直径小于船-矢量推进器系统对应喷管偏角时的战术直径，但在大舵角（喷管偏角）情况下，船-矢量推进器系统对应的战术直径更小，而船-舵-矢量推进器系统的战术直径最小，与图4（e）对比可以看出，对于船-舵-推进器系统，控制轴向航速可以减小战术直径，对于船-矢量推进器系统，在小喷管偏角情况下，控制轴向航速会增大战术直径，但在大喷管偏角情况下，控制轴向航速可以减小战术直径；对于船-舵-矢量推进器系统，在大舵角、大喷管偏角情况下，控制轴向航速可以减小战术直径，但在小舵角、小喷管偏角情况下，控制轴向航速会增大战术直径。总的来说，对于船-舵-矢量推进器系统，控制轴向航速可以有效提高大舵角（喷管偏角）情况下潜航器的回转性能，以舵与矢量喷管偏角均为40°时为例，控制轴向航速时，回转周期由95.99 s减小至54.45 s，纵距由166.5 m 减小至159.4 m，正横距由70.4 m 减小至37.5 m，战术直径由228.5 m 减小至102.8 m。

通过对图5中数据进行非线性拟合，采用rational2D 拟合方法，建立回转半径Rs、回转周期T、纵距La、正横距Ld、战术直径DT随舵角δr、喷管偏角δn变化的数学模型:

3 结 语

本文研究的是船-舵-推进器、船-矢量推进器和船-舵-矢量推进器三种不同的控制方法时潜航器的回转性能，通过对低航速、控制泵喷推进器转速、控制潜航器轴向航速三种不同条件下潜航器做水平面回转运动进行仿真，证明了矢量推进器可以改善潜航器的回转性能，船-舵-矢量推进器系统更是可以大幅度提高潜航器的回转性能，另一方面，通过控制潜航器轴向航速可以在以提高能耗为代价的前提下提高潜航器的回转性能。本研究结果可以为潜航器的操纵方式提供有价值的参考。