一道2023年IMO不等式试题的解法与推广

江智如 蔡 珺

福建省南平市高级中学 (353000)

1 试题呈现

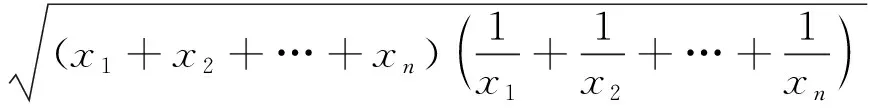
本试题是2023年第64届IMO第4题．从an的表达式容易想到Cauchy-Schwarz不等式,可得an>n,等号不成立,于是a2023>2023,与试题结论相异,所以改变思路方向,考虑递推关系式．

又an+1=

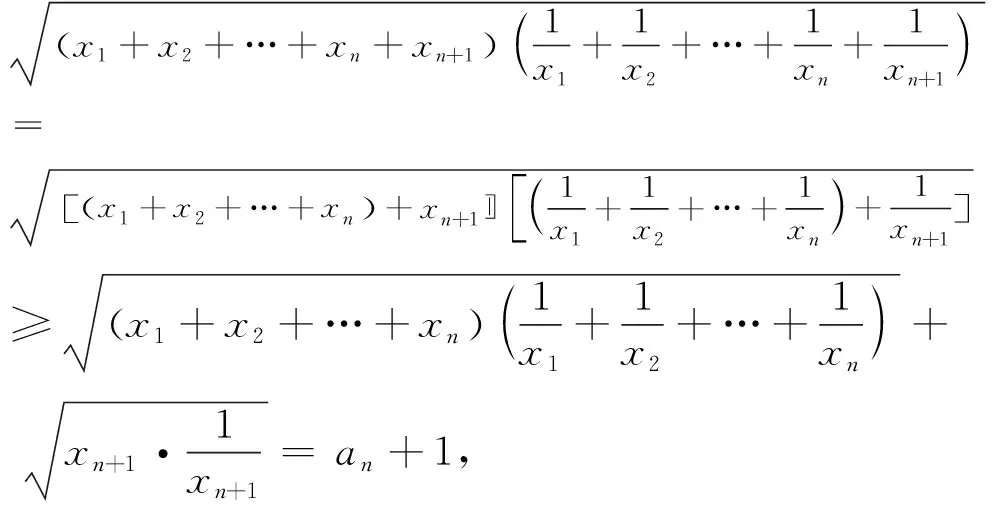
2 解法探究

解法1：(利用Cauchy-Schwarz不等式证明[1])

解法2：(利用数学归纳法证明)由分析可知a2023≥2023,而3034-2023=1011,故2023=2×1011+1,3034=3×1011+1．

下面先归纳证明:a2m+1≥3m+1,其中m=1,2,…,1011．

(i)当m=1时,a3=

=3,其中x1,x2,x3两两不等,故等号不成立．

又a3∈Z,故由整数的离散性可得a3≥4,所以原不等式成立．

(ii)假设m=k,k=1,2,…,1010时,不等式成立,即a2k+1≥3k+1．那么,a2(k+1)+1=a2k+3=

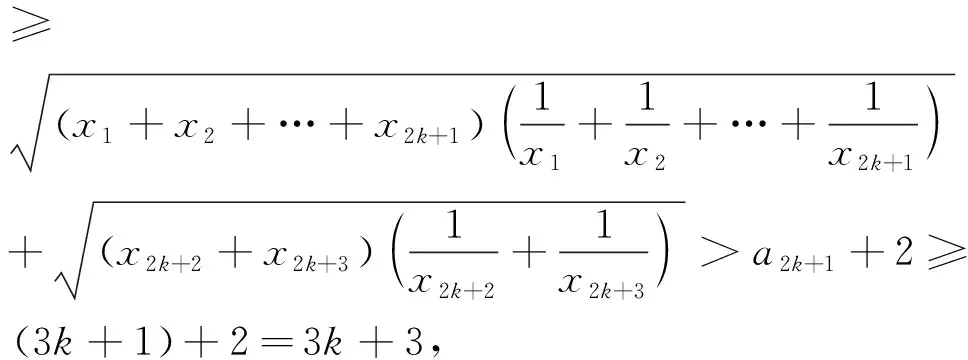
所以,由(i)(ii)知,对m=1,2,…,1011,a2m+1≥3m+1均成立,因此,当m=1011时,a2023≥3034成立．

3 推广

由解法2的证明过程,我们可以将m取值范围推广到全体正整数,得到试题的推广形式[2]:

结论：设x1,x2,…,xn,…,是一组两两不等的无穷正实数列,若对∀n∈N*,an=

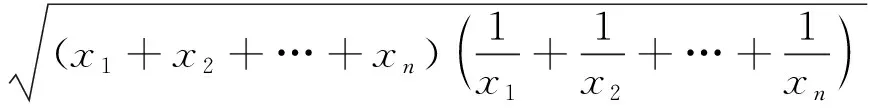
本结论是原试题的推广,但使用范围更广．