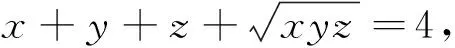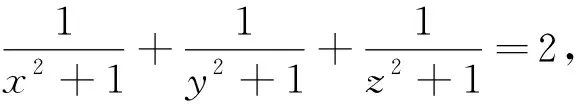一道数学奥林匹克选拔题的探究与推广

郑剑晖

福建省莆田第五中学 (351100)

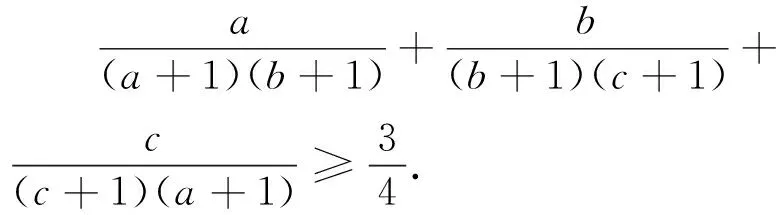
本题内涵丰富,由之可得到一些有用的结论,并进一步变换出一系列数学竞赛试题和数学问题.

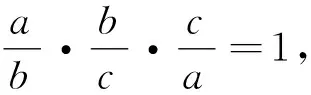
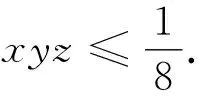
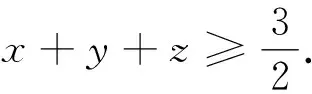
结论3 设x,y,z是正实数,且xy+yz+zx+2xyz=1,则x+y+z≥2(xy+yz+zx).

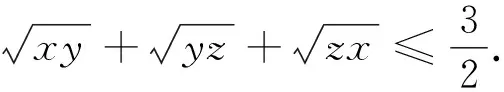
由以上结论还可以变换出一系列数学问题.

题1 (2014年罗马尼亚数学竞赛试题)已知x,y,z>0,且xyz+xy+yz+zx=4,求证:x+y+z≥3.

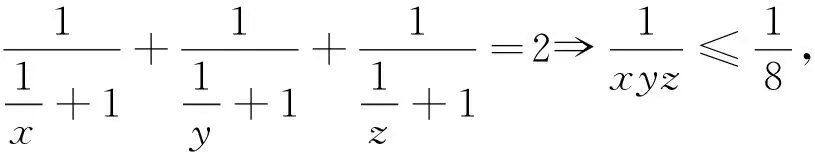
这就分别得到并证明了如下试题:

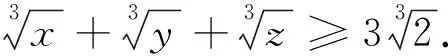
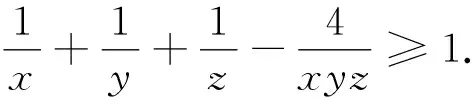
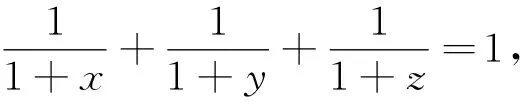
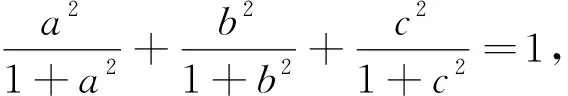
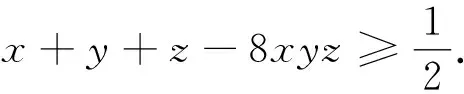
题7 (2004年地中海地区数学奥林匹克试题)已知x,y,z是正数,且xy+yz+zx+2xyz=1,证明:2(x+y+z)+1≥32xyz.

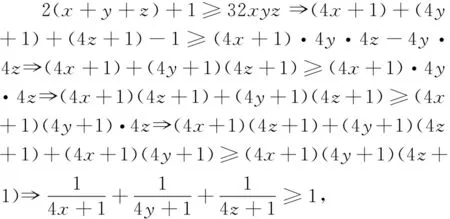
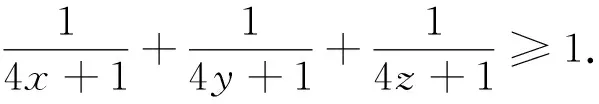
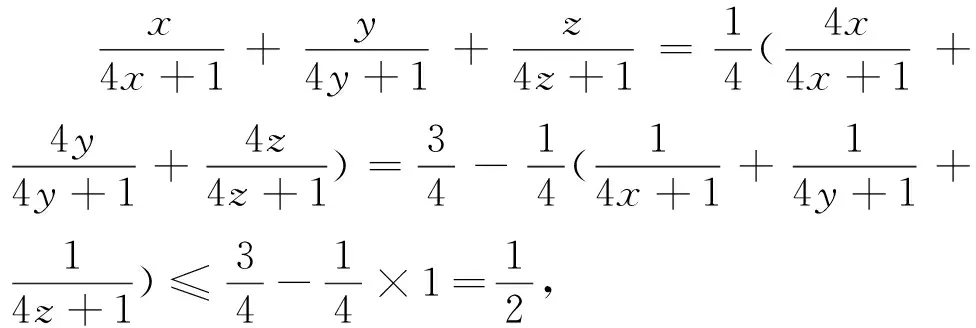
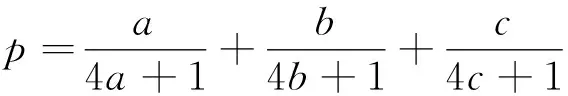
题10 (2005年哈萨克斯坦数学奥林匹克试题)已知a,b,c>0,且abc=a+b+c+2,求证ab+bc+ca≥2(a+b+c).

题11 (1996年越南数学奥林匹克试题)设x,y,z∈R+,且xy+yz+zx+xyz=4,证明:x+y+z≥xy+yz+zx.