非对称韦达结构问题的处理策略——以2023年全国新高考II卷第21题为例

刘旭飞

浙江省温州中学 (325014)

一、真题呈现

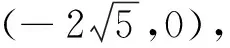
本题考查了双曲线的标准方程,直线与双曲线的位置关系,意在考查学生数形结合的数学思想和运算求解能力,对考生的逻辑思维能力、分析问题和解决问题的能力有较高的要求,试题解法多样,内涵丰富,突出选拔功能,是一道非常好的高考压轴题.

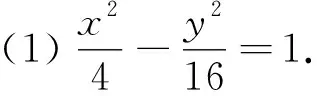
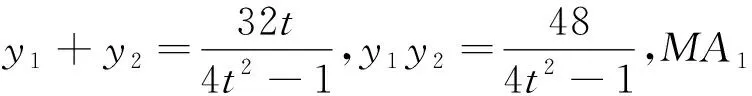
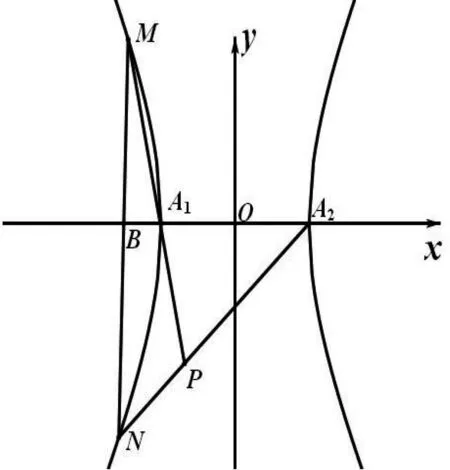
图1

二、多角度处理

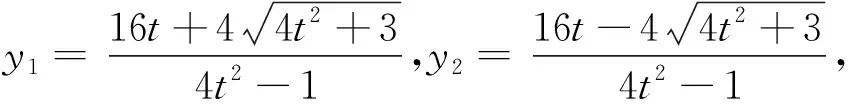
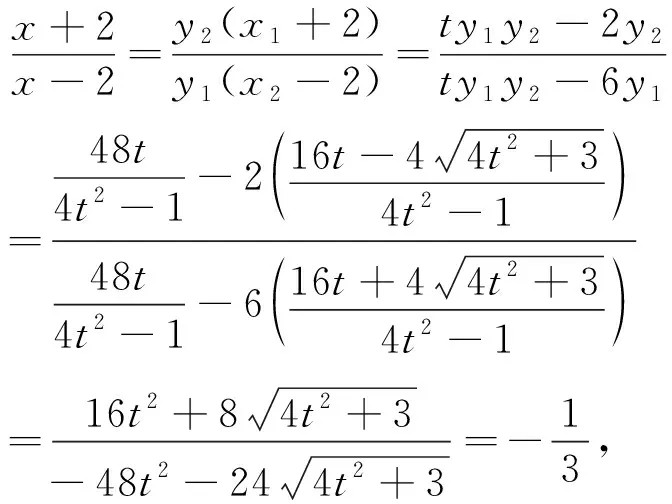
评注：式子中对称的用韦达代入,不对称的部分求根公式代入,其本质是整体消元,对学生的运算能力有较高的要求.

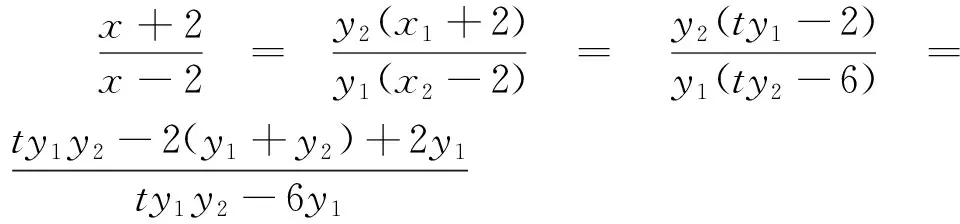
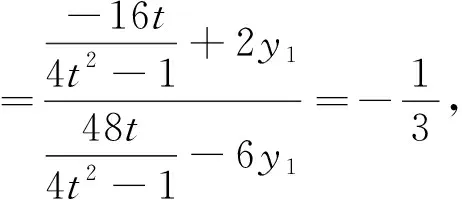
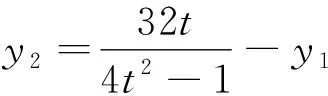
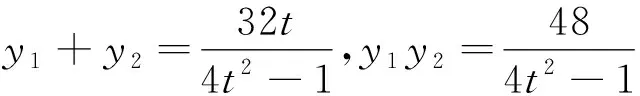
评注：利用3(y1+y2)=2ty1y2将二次式y1y2化为一次式y1+y2,实现了次数的统一,大大降低了运算量.

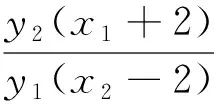
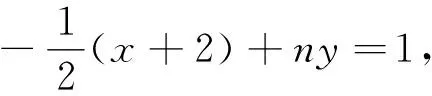
评注：构造对偶式巧妙避开了非对称韦达结构,化非对称为对称,其难点是对偶式的构造,对于本题需发现M,N互换位置结论的不变性,也就是摆脱点M在第二象限的束缚.

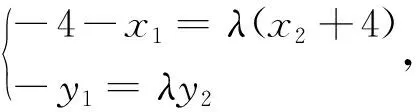
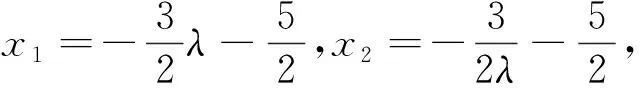
评注：利用定比点差法求得M,N的坐标,进而得到MA1,NA2斜率之间的关系,有效的避开了非对称形式,不失为一种巧方法.

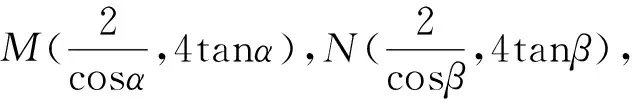
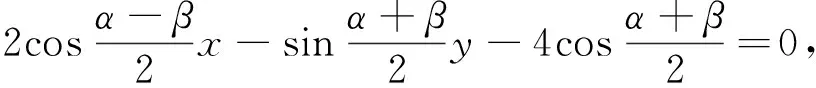
评注：利用曲线的参数处理此类问题有效避开了非对称结构,但参数方程对三角恒等变换的要求很高,尤其是和差化积等公式的灵活运用更是解决问题的关键.

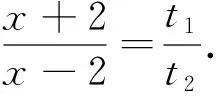
评注：利用曲线系的方程求解有效的避开了非对称结构,但需熟练掌握曲线系的相关知识,对学生的知识储备有较高的要求.

解析几何中的非对称问题是学生学习的难点,也是教学的难点,本文所归纳的9种方法是处理此类问题常见的方法,感兴趣的读者,可尝试用以上方法求解近年的高考题.