恒成立巧切入,多方法妙应用—一道函数不等式综合题解法的探究

朱 梅

江苏省高邮第一中学 (225600)

含参不等式恒成立问题一直是高考数学中的一类热点题型,有时以小题(选择题或填空题)形式出现,有时以解答题形式出现,均是难得的压轴题.此类问题难度较大,解题思维灵活多变,创新新颖,是充分体现考生的基础知识、基本能力与解题经验等方面的一个很好场景,具有较好的选拔性与区分度,倍受关注．

1．问题呈现

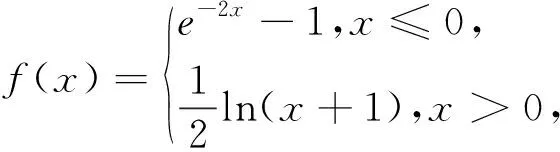
这是一道以指数函数、对数函数混合的分段函数为问题背景,结合含参不等式恒成立来创设问题场景,进而确定相关参数的取值范围．

2．问题破解

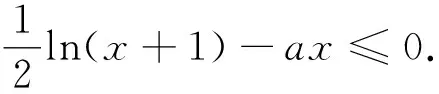
解后反思：根据题设条件中的分段函数,分x=0,x<0及x>0三种情况分别讨论,通过不等式的恒等变形与转化,合理构造函数,结合x=0处的函数值,推导得出函数的单调性,进而得出导函数的符号,分离参数加以合理转化与应用,即可推得答案．

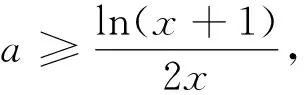
解后反思：根据题设条件中的分段函数以及对应的不等式加以分类讨论,利用切线不等式来合理放缩,简捷有效,是破解此类问题的一种“巧技妙法”．利用切线不等式放缩解决不等式恒成立问题确实能达到事半功倍的效果,但是并非所有的不等式恒成立问题可以使用此方法．注意到本题等号成立的条件是x=0时,而两个函数刚好都是在x=0处有切线．因此一般来讲,利用切线不等式放缩是在取等号处寻找切线．

3．变式拓展

变式1 已知函数f(x)=

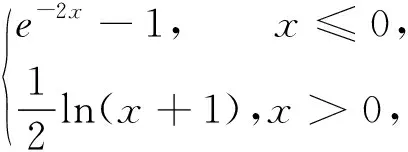
解析：对函数y=e-2x-1求导可得y′=

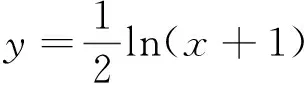
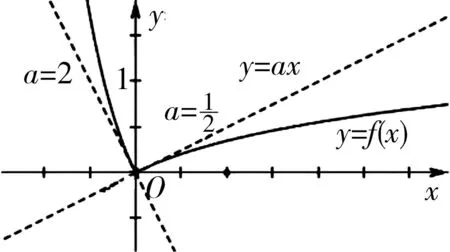
图1

评注：利用导数的几何意义,回归分段函数中在端点x=0处的切线的斜率确定,数形结合,直观分析参数的取值范围问题,难度中等．

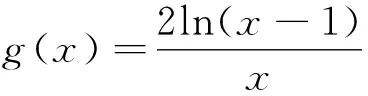
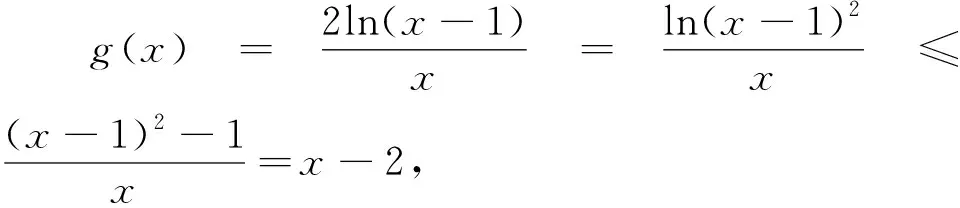
评注：结合切线不等式分别对不确定的函数f(x)与确定的函数g(x)进行放缩处理,恰好两曲线位于两平行直线的两侧,转化为求解两平行线间的距离来转化,难度太大．

4 教学启示

破解此类含参数不等式恒成立问题,常见的解题技法主要从以下几个方面切入:一是函数视角切入,基本的技巧策略是构造函数法,利用函数的单调性与最值来巧妙转化;二是不等式视角切入,基本的技巧策略是借助不等式基本性质或重要不等式(包括切线不等式等)的放缩来转化;三是数形直观切入,基本的技巧策略是通过函数图象的数形结合法来直观转化等．