抽丝剥茧 凸显本质——“多元问题”求解教学的实践与思考

张志华

江苏省南通市海门证大中学 (226100)

多元问题求解是一个比较难处理的问题,学生常常因为找不到合理的切入点而失去解题信心.其之所以难主要是难在“多元”上,解决此类问题最直接、最有效的方法就是“减元”,即将多元问题转化为学生熟悉的两元或一元问题,从而通过化多为少、化繁为简的转化,降低问题的难度,提高解决效率.本文是笔者在二轮复习时,以“减元”为抓手,对多元问题的求解进行了教学实践,并总结了几点认识,现与同仁分享交流.

一、教学过程

1、问题初探,形成策略

课始,教师给出如下两个问题让学生独立完成.

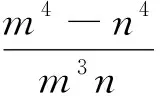
以上两个题目有一定难度,不过对于二轮复习的学生来说,他们已经具有丰富的处理恒成立和齐次式的处理经验,所以问题给出后,学生很快就找到了解题思路.10分钟左右,大部分学生已经得到了答案.

师:谁来说一说,对于例1,你是如何求解的?

师:很好,例2你们又是如何求解的呢?

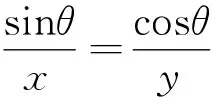
师:非常好.以上两题都是多元问题,具有一定难度.分析以上两位同学的解题过程,看看他们是怎么解决这个难题的?以上两种解法有何共同之处呢?

生3:以上两个问题至少有三个量,不过解到最后就变成了一个量.

师:非常好,生3抓住了问题的关键,两位同学在解题时将多元问题转化为一元问题,使问题向简单化、清晰化转化,顺利地解决了问题.在解决多元问题时,要想尽办法减元,从而将多元问题转化为我们熟悉的二元或一元问题.那么具体如何来减元呢?这个就是我们今天要研究的主题.

设计思路:从学生熟悉的恒成立和齐次式问题出发,通过问题的解决让学生发现解决多元问题的常见策略即“减元”,继而引出本课的主题.同时,以上问题虽略有难度,但是学生只要认真分析完全可以顺利求解的,由此提升后续学习的信心.

2、问题再探,提炼方法

师:接下来我们看看例3该如何求解呢?

例3 已知x,y,z∈R,且x+y+z=1,x2+y2+z2=3,则xyz的最大值为.

学生独立思考,交流解题思路.

生3:由x+y+z=1变形得x+y=1-z①.将x+y+z=1两边平方得x2+y2+z2+2(xy+yz+xz)=1,又x2+y2+z2=3,故xy+yz+xz=-1,继续变形得xy+z(x+y)=-1,此时将①代入得xy+z(1-z)=-1,xy=-z(1-z)-1,可见xy可以用z表示,即xyz=z3-z2-z.

师:很好,思路清晰.在减元策略的指导下,经过几次变换最终将所求的xy用z表示,从而将三元问题转化为我们熟悉的一元问题.其实以上策略也就是我们经常说的“消元”.

师:通过“等式消元”,将所求转化为了关于z的函数,那么函数的定义域如何求呢?

师:要求函数的定义域,实则求z的取值范围.大家看看在已知条件和由已知条件变形的式子中,是否能够找到关于z的不等式呢?

生4:因为x2+y2≥2xy,这样若将左右两边都有z表示,则可以得到关于z的不等关系,求得

师:非常好,联想基本不等式公式发现了隐含于题设之中的关于z的不等关系,得到了z的范围.分析至此,问题即可迎刃而解,课下请大家将解题过程补充完整.

师:回顾以上解题过程,你认为解决此类问题还难吗?如果遇到此类问题你该如何做呢?

生5:消元是解决此类问题的重要工具,以后在遇到多元问题时,要想着将某个量用其它量表示出来.有些题目可能需要几次变形后才能实现消元,不过只要我们有着坚定的信心,并朝着正确的方向去思考,一定可以顺利求解.

师:说得非常好!在解例3时,我们利用“等式消元”实现了“减元”的目标,那么如果条件中没有等式,我们又该怎么办呢?现在请大家看看例4该如何求解呢?

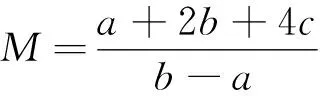
同样,教师预留5分钟让学生独立思考后,师生互动交流.

生6:根据已知我得到了两个不等关系,即a>0,Δ=b2-4ac≤0,没有等量关系,所以我不知道怎么转换.

师:能够得到两个不等式也很不错.这里没有等式可以利用,我们该如何往下进行呢?

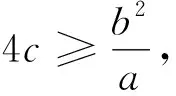
师:非常好,看来除了应用等式消元外,还可以应用不等式消元来实现“减元”的目标.结合以上分析不难发现,整体代换也是消元的一种常用方式,可以达到“减元”的目的.

师:下列的例5是否可以按照以上思路求解呢?

例5 已知ΔABC三边长a、b、c成等差数列,且a2+b2+c2=84,求实数b的取值范围.

师:例5采用什么方法可以达到减元的目的呢?直接利用等式消元吗?

生8:因为三边ΔABC的三边长成等差数列,通过设公差可以达到减元的目的.不妨设a≤b≤c,公差为d,所以有a=b-d,c=b+d,这样就将三元问题转化为两元问题,代入等式得3b2+2d2=84.

师:非常好,以公差为媒介,实现了减元的效果.接下来该如何求呢?

师:非常好,这样利用不等式消元解决了问题.从刚刚解题反馈来看,大多数学生都想到借助介质变量“d”来达到减元的目的,不过有些学生却没有走到最后,这说明了什么呢?

生9:减元只是第一步,还要利用a、b、c构造三角形这一条件.

师:非常好,多元问题其实是综合性问题,通过“减元”可以剥开问题神秘的面纱,但是具体问题的解决还具体分析.如例3、例4对应的是函数的最值问题,而例5是三角形问题,其所考查的是学生的综合能力.

设计思路:教师给出典型例题让学生体会、感悟、概括,提炼“减元”方法,提升学生综合素养。同时让学生通过经历“减元”的过程,逐渐消除学生的畏难情绪,增加学生解题信心。在此过程中,教师充分发挥教育的育人功能,重视培养学生敢于探索,勇于实践的良好学习习惯,帮助学生形成正确的学习观.

二、教学思考

实际教学中,许多学生在面对“多元问题”求解时常常会出现畏难情绪,而“减元”是解决多元问题的最容易想到的常用解决策略,为此教师以“减元”为主线,借助典型例题与学生共同探讨减元的方法,以此为多元问题的解决架桥铺路.其实“多元”只是一个表象,而问题的实质常常被这些“表象”所掩盖,只有揭开多元问题的“外衣”,才能使问题的本质显现出来,帮助学生找到解决问题的正确方法.例如,以上例题中,拨开多元的“外衣”后,函数、不等式、线性规划等内容就显露了出来,让学生找到了正确解题的方向,顺利地解决了问题.多元问题之所以难不仅仅因为“多元”,还因为其涉及的知识点多,综合性强,对学生逻辑推理、直观想象、数学运算等综合能力要求高,所以要解决此类问题既要有扎实的基础知识,还需要很强的综合素质.