基于跨地域最优的水资源配置双层多目标模型研究

李 莉，李伟青，黎耀华，杨泽斌

（1.惠州学院 数学与统计学院； 2.惠州学院 电子信息与电气工程学院，广东 惠州 516007）

随着人口的不断增加，人们对水资源的需求量也日渐激增，而随着对水资源的不合理开采和利用，最终很多国家出现不同程度的缺水问题。针对水资源配置方法，郝奇琛等［1］结合多种水源以及供水能力和供需关系等制约因素，构建了厦门市多水源联合分配模型；李俊［2］等应用NSGAIII-NSGAII 多目标模型建立了水资源配置双层模型并得出最优方案；王瑶瑶等［3］利用Mike Basin 模型软件搭建流域水资源配置模型并利用多目标规划的方法求解得出最优方案；向龙等［4］选取多个目标函数构建了不确定性模糊多目标规划(IFMOP)水资源配置模型，并计算了不确定性解集以解决水资源配置问题。可见，在处理水资源配置问题时，多向的供水目标使得模型中应设立多个目标函数以及多个约束条件，以便得到最优供水方案。

除了水源短缺，在很大程度上缺水是因调水跨度大使得水资源得不到科学分配和合理利用所造成［5-6］。因此，跨地域最优是对水资源合理开发和提高利用效率的重要方向。当下对于小范围地域水资源配置已有许多学者给出自己的解决方案，而面对跨地域广、多水源多目标的水资源配置问题的论文还相对较少；因此本文针对此类问题提出一种双层多目标规划模型，为解决跨地域水资源配置问题提供一种新思路。

1 研究区概况

本文主要针对多供水地多需水地远距离供水问题进行方法研究和分析。为方便计算，在下文中假设一种2 供水地5 需水地的情况用以计算分析，其中以2个水库作为供水地进行供水（降雨量与地下水量均不纳入考虑范围），同时将5 个需水地分别拆分为工业、农业、日常生活以及生态需水量4 个方面作为直接供水对象，各需水地与供水地之间的距离也各不相等，跨度不一，符合实际情况。

2 研究方法

2.1 研究方法及思路

多目标规划模型是一种以多个目标变量为基础的最优化模型，其主要用于求解多个目标函数的优化问题，能够有效的解决复杂系统中多个目标之间的冲突问题。

双层规划模型是一种上下2 层递阶关系结构的数学模型，在交通运输、资源分配、工程设计等方面均得到了很好的应用成果［7］，由于可持续发展已成为社会经济发展的一个基本原则，水资源优化配置必须在此原则的基础上对各方面因素进行全局考虑，确保整体综合效益最大化［8］。

本文将选取由双层系统衍生出的双层多目标规划建立模型，其中双层规划中上层目标函数可由政策确定，下层目标函数可由多目标规划建立，得到一个可随时调整效益侧重的双层多目标规划模型。将传输、生态、环境、社会、经济5 个效益目标作为下层目标函数，并以供需水地的水资源配置政策及就近原则作为上层决策原则，将需水地的用水户分为4 个方面，其他方面不计入考虑。

由于上层目标是根据需水地相关政策完成决策作用，因此无法得出上层目标函数的数学表达式，而下层的目标函数可以由供水量表示出其具体数学表达式，为了减少求解模型的工作量，可以先将下层的目标函数通过遗传算法求出最优解集，即各地的供水量，再让这些解提供给上层政策作出具体配置水量，经此，便能解决多供水地给多个需水地的具体水量配置问题，同时也解决了实际实施配置水量的可行性问题。

最后，通过该模型给出3 种不同要求下的方案：（1）生态环境型：为达到生态环境效益目标最高的水资源配置。（2）经济型：为达到经济效益目标最高的水资源配置。（3）综合型：同时考虑生态环境效益与经济效益的水资源配置。

2.2 跨地域最优水资源双层规划模型

分别将供水层和需水层作为双层模型中的上层和下层，下层以包括传输效益目标在内的五个效益目标作为目标函数，将水源地的可供水量和需水地各用户需水量作为主要约束条件；上层以供需水地的水资源配置政策及就近原则作为上层决策原则，把下层目标函数计算得出的水配置总量作为调用各水源地供水量的约束条件。通过上下两层之间的相互牵制，形成一个可行性强、选择面广、配置灵活的跨地域最优水资源双层规划模型。下面是具体说明及相关的数学表达式。

2.2.1 双层规划模型约束条件

2.2.1.1 需水层约束条件

（1）可供水量约束：第i个水源供给k地区j用水户的水量之和不能超过水源i的可供水量。

式中I、J分别表示水源总数、用水户总数；所有水量单位为m3。

（2）需水量约束：k地区j用水户的供水量在该地区j用水户的最小需水量和最大需水量之间。

（3）变量非负约束：

2.2.1.2 供水层约束条件：

式（4）中为i水源地向k地区的总供水量，式(5)中为表1 中应分配给k地区j用水户的权重，K为需水地数量。

表1 各城市各用水户年需水量 m3

2.2.2 双层规划模型目标函数

2.2.2.1 需水层目标函数

（1）社会效益目标

社会效益目标是在综合考虑经济和社会等因素的基础上，通过合理的管理与利用，从而最大化的对社会的利益和福利产生积极影响。由于不同地区的缺水情况会在不同程度上影响着社会稳定与该地区的经济发展，而其缺水量是由该地区的供水总量和用水户的需水总量和所决定的，其中每个用水户的需水量均包括生活、生产、生态用水3 个方面，因此本文将缺水量最小作为社会效益最优的标志［9］，其目标函数为：

式中：为k地区j用水户的平均需水量(单位: m3)。

（2）经济效益目标

经济效益目标是通过提高资源利用率和合理定价与税费机制等手段实现经济效益的最大化。本文以单方供水产生的经济效益达到最大作为其经济效益目标，先得出某一地区某一用水户的供水量与各水源地对应的供水净效益系数乘积之和，再将其同该用水户的权重系数与基尼系数的乘积作为其经济效益，总经济效益则为所有用水户的经济效益之和，其目标函数为：

式中：指供水效益系数，由k地区j用水户需水量与生产值的比值决定，表示k地区j用水户从i水源地单位取水量的效益（元/m3）；指供水费用系数，表示k地区j用水户从i水源地单位取水量的费用（元/m3）；指第k个指标的权重系数，表示k个不同指标对用水量分配公平性影响的重要程度；指第k个指标的基尼系数。

（3）生态效益目标

考虑到在进行水资源配置时，由不同水源向不同地区进行供水的过程中，其生态环境存在着不同程度的生态用水需求，因此将区域生态环境供水量与需水量的比值作为研究区域水资源配置的生态效益目标，其目标函数为：

式中：为i水源地向k地区生态环境方面的供水量，为k地区的生态需水量(单位: m3)。

（4）环境效益目标

环境效益与日常生活息息相关，其中生活污水、工业污水和农业污水在一定程度上破坏环境，降低环境效益，因此，将各地区各用水户的最终污水排放量之和最小作为环境效益目标，其中最终污水排放量表示为各地区各用水户的供水量、污水排放率与污水残余率三者之积，具体目标函数为：

式中：为k地区j用户的污水排放率；指k地区j用水户的污水处理率。

（5）传输效益目标

传输效益目标是通过合理的资源调度与传输安排，在不同地区之间实现资源有效传输与利用和综合利益最大化。传输效益由运输总量和地域跨度共同决定，由于本文讨论的供需水地点地理跨度大，总输水量多，使水源地与各地区间的水资源运输成本不可忽略处理，若将同一地区不同用水户之间的运输成本忽略且保证各地区运输一立方水的成本均相同，则有：当2 个地区总供水量相同时，与同一水源地距离越远则传输成本越高；同理，当2 个地区与同一水源地距离相同时，总供水量越大时其传输成本越高。因此，先计算出各个地区所有用水户的总供水量与不同水源地相隔距离的乘积，再将各地区的乘积之和作为传输效益目标，其目标函数为：

式中为i水源地与k地区之间的直线距离（单位:m）。

（6）综合效益目标

综合效益目标函数是将上述5 个效益进行综合分析得到的多目标规划统一值，将综合效益目标作为下层目标，其目标函数为：

式中α1、α2、α3、α4、α5分别表示社会效益、经济效益、生态效益、环境效益和传输效益的权重值。

各类效益权重值采用层次分析法［10］确定，对于生态环境型，社会效益、经济效益、生态效益、环境效益和传输效益的权重比取4:2:5:5:4；对于经济型，其比值取2:4:1:1:2；对于综合型，其比值取1:1:1:1:1。经线性加权法转化后的综合效益目标函数为：

2.2.2.2 供水层目标函数

供水层以需水地的水资源配置政策作为上层目标。

2.2.3 双层规划模型求解思路及方法

2.2.3.1 求解问题概述及思路

一般双层规划问题作为NP-head 问题，其求解方法较为困难［11］，但本文双层规划模型的上层（供水层）的目标函数无法以函数形式确定，故可以先将下层（需水层）的最优解集求出，再根据需水地的有关水资源调度政策确定具体配置情况。

由2.2.2.1 节的内容，下层目标函数可列为下式

式中α1、α2、α3、α4、α5均为常量，由缺水地相关政策决定。当缺水地对生态环境要求较高时可将α3、α4提高，同理对于更需要经济效益目标的缺水地，可以将α2提高，将其他方面的权值降低。这样便能实现上层决定方向，下层决定起点的双层控制模式。

2.2.3.2 模型求解方法

遗传算法对求解的问题本身没有任何要求，也不需要严苛的数学假设（如连续可导等），并且具有固有的隐式并行性和更好的全局优化能力［12］，适合大规模复杂问题的优化。利用遗传算法的这些特性，可以很好地求出本文中下层目标函数最优解集。

MATLAB 使用版本为 2020b，求解器选择gamultiobj——使用遗传算法的多目标优化［13］，求解器算法设置选项中添加混合优化器fgoalattain，提升优化效果;交叉函数选为crossoverarithmetic，其他值均为默认值。

3 双层规划模型验证

3.1 算例概述及求解

设有2 个水库需向5 个城市供水，其中1、2 号水库现储水量分别为220、230 亿m3。5 个城市的工业、农业、日常生活以及生态需水量如表1所示(为省篇幅，具体数值只取4 位有效数字，同时不足1 m3的水量取0，表3 同)；对于各个城市的供水效益系数、用水公平系数以及2 个水库到5 个城市的距离如表2 所示。

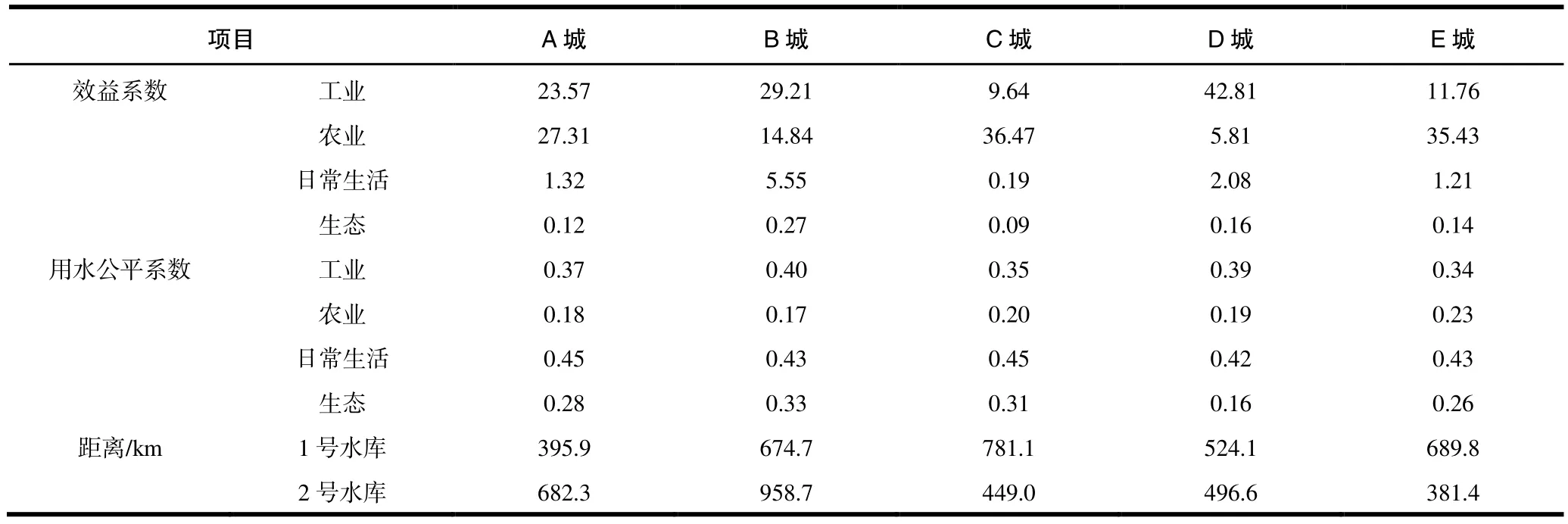
表2 各城市供水效益系数、用水公平系数，水库与城市之间的距离

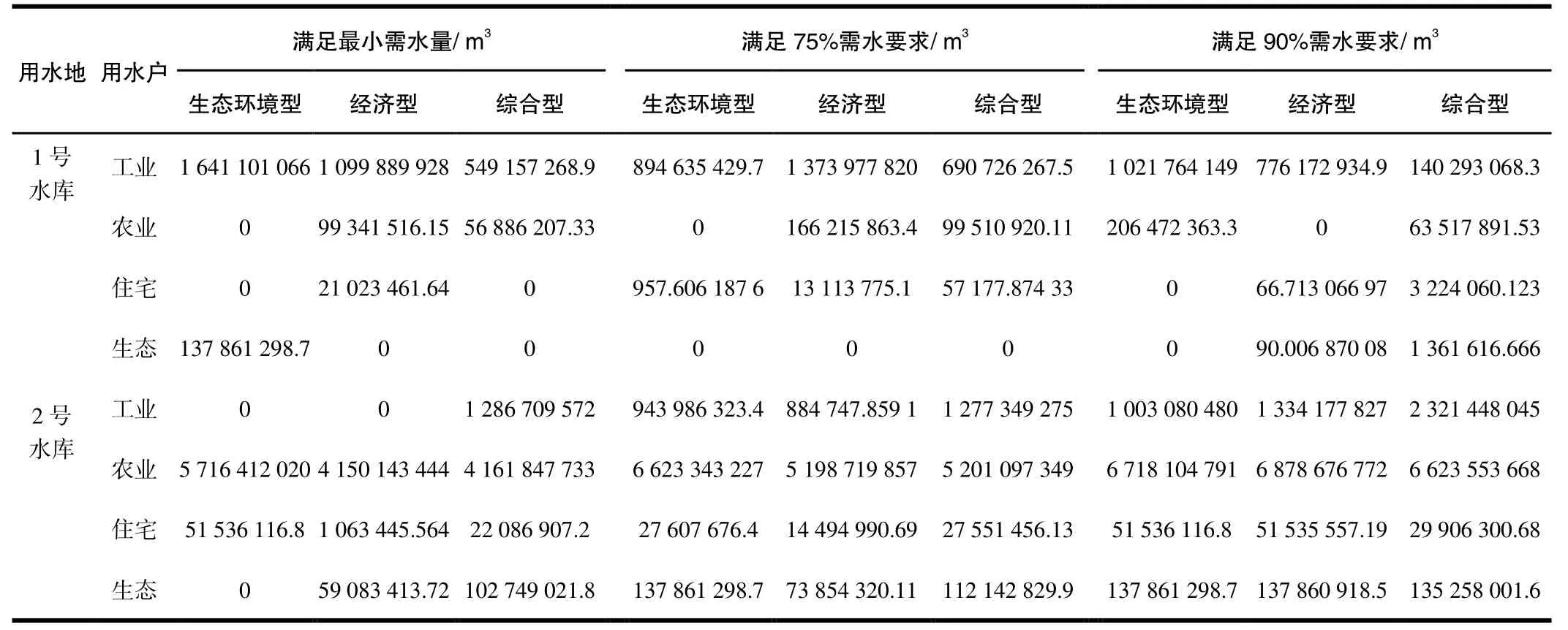
表3 C 城最优供水方案

将数据代入(16)式中求解可得各方案的最优供水量(不足1 m3的供水量取0)，由于城市数量较多，为省篇幅，以下仅列出2 个水库对于C 城的最优供水量:

在不同供水方案下计算最优供水效益，结果如表4。

表4 最优供水效益

3.2 算例结果分析

3.2.1 供水方案角度分析

（1）生态环境型方案相较于经济型方案，满足最小、75%、90% 需水量时总缺水量分别低于后者1 380 871 227m3、505 77 6 342 m3、75 296 609 m3的水量。这是因为工农业供水效益系数较大，同时需水量也较多，使经济型方案总供水量较多，故总缺水量较少，即社会效益明显更低，与实际情况相符。

（2）对于同一个供水要求，生态环境型方案的生态效益、环境效益明显优于经济型方案，同时其经济效益明显劣于经济型方案。这在供水要求最低时尤为显著，在只满足最小需水量时，生态环境型方案的生态供需水量之比约为6.86，而经济型方案的生态供需水量之比仅为3.00；在污水排放量上，经济型方案比生态环境型方案多排放了1 125 028 230 m3的污水量；在盈利值上，经济型方案比生态环境型方案多盈利44 374 368 501 元。同时，综合型方案的三种效益指标均有着最优的总效益值，是最均衡的解决方案。

（3）当需水量要求逐渐变高时，供水量随之变大，使传输水量无法避免地变大。由（1）、（2）可知，经济型方案的总需水量最大，因此在同一供水要求条件下，经济型方案的传输效益最高；此外，由于给工业的供水量增加，故经济型方案的污水量也相对更高，即环境效益值更高，当供水要求提高时，各方案的环境效益值也随之提高，与实际情况相符。

（4）在大部分供水方案下，均有出现部分地区个别用水户仅由一个水库供水(另一个水库供水量为0)，同时2号水库总供水量比1号水库总供水量多的情况。这是因为2 号水库离各城市的总距离较近，故总供水量更大。说明在求解最优供水方案时，距离也是算法考虑的因素，这侧面反映了算法与模型的可行性。

3.2.2 供水效益角度分析

（1）从上述5 种效益图（图1 至图5）纵向观察可知，对于任意一种供水方案，其需水量要求越高时：①缺水量越小，社会效益越好；②盈利值越大，经济效益越好；③水量供需比越大，生态效益越好；④最终污水量越大，环境效益越差；⑤供水量与供水距离的乘积越大，传输效益越差。上述结果表明，模型求解后的结果与实际情况相符，有一定的可行性。

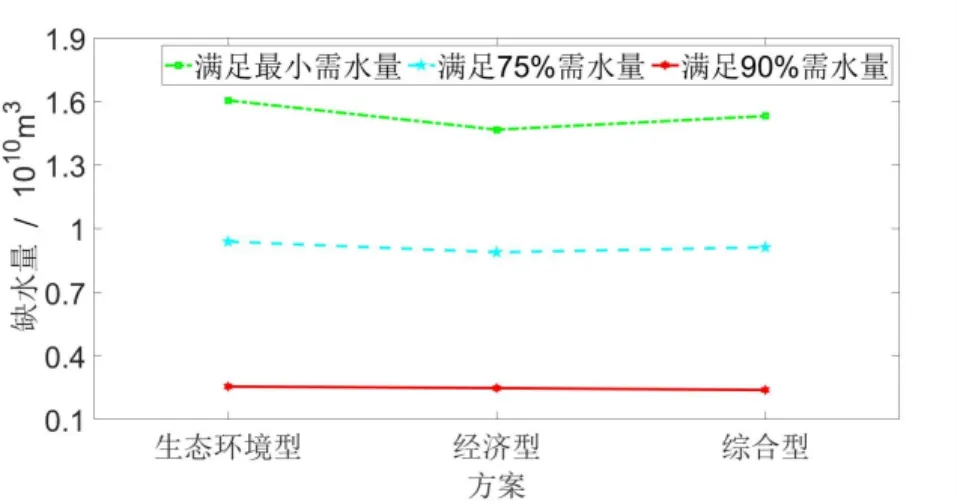
图1 社会效益

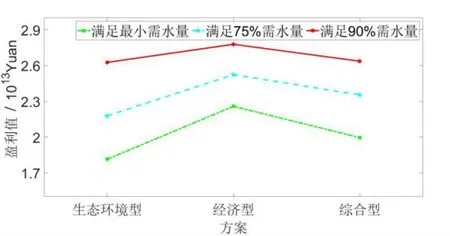
图2 经济效益

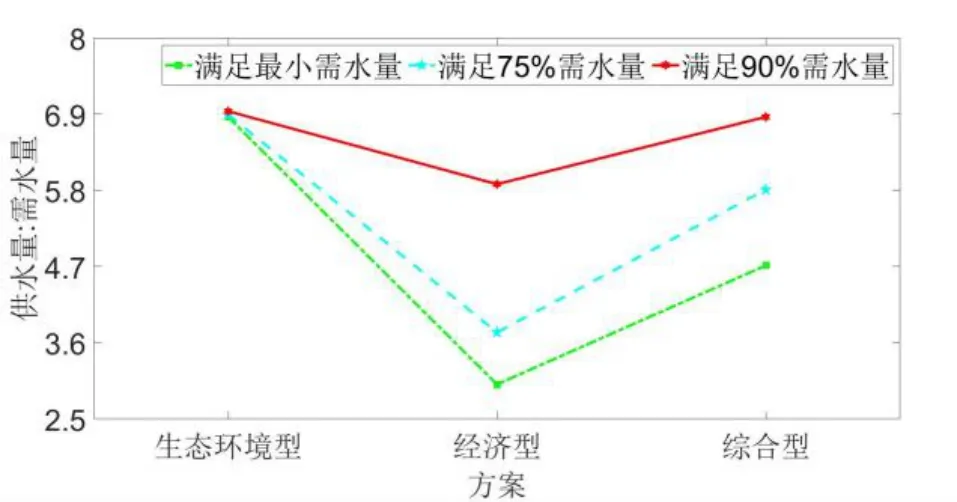
图3 生态效益

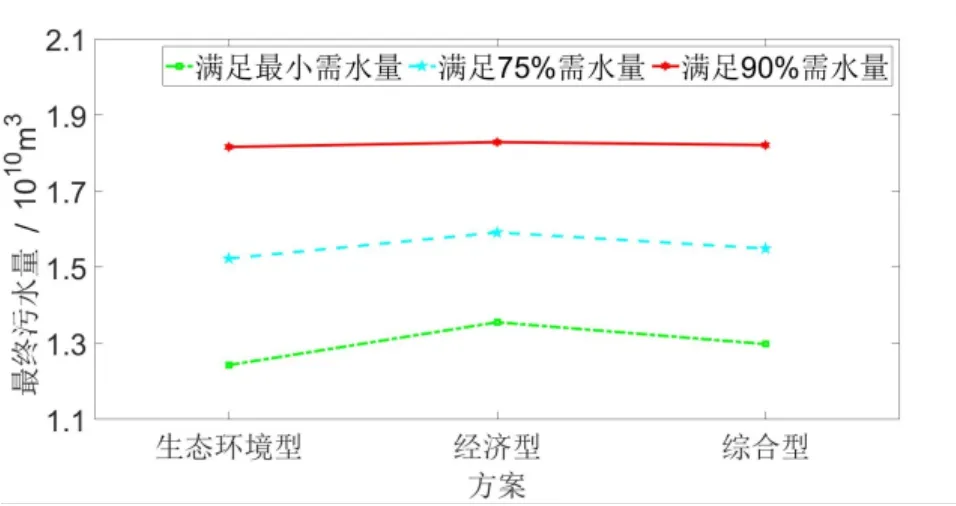
图4 环境效益

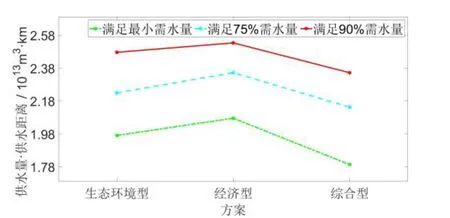
图5 传输效益

（2）当需水量要求越高时，3 种供水方案的各项效益值差距越小，该现象在社会效益和环境效益时表现尤为明显。这表明，当供水地可用供水量越少时，选用经济型方案时与选用生态环境型方案时的各项效益值差距将越大。因此对该地区变化（生态环境变好/经济盈利值变高）也将更为明显，此时选用综合型方案方为最优方案。

（3）观察综合型方案产生的效益发现，在任意需水量下，其社会、经济、生态以及环境效益值均位于另外2 种方案所产生的效益值之间，而传输效益值例外，采用生态环境型方案与经济型方案所产生的传输效益值均比综合型方案的高。因此，选用综合型方案将为上层决策节省一定的传输成本，实用性更强，从而达到跨地域最优水资源分配的目标。

3 结论

本文针对跨地域水资源配置存在时空分布不均，传输距离相差较大导致传输成本较高的问题，提出了一种上层目标函数由政策确定、下层目标函数由含有传输效益目标的多目标规划建立的双层多目标模型，并通过遗传算法得到最优配置方案。从算例结果分析中验证了模型的合理性、实用性和通用性；观察表2、表3 数据，存在个别用水户由某一水库供给的水量为零的情况，这表明模型在演算时综合考虑了传输效益目标的影响，使得综合效益趋于最优解，即本文提出的双层多目标模型能够解决水资源跨地域配置最优问题，实现水资源的有效传输与利用，降低成本，达到综合效益最大化。因此本模型能为跨地域水资源配置问题的解决提供一定的思路。