分层变模量下的沥青路面车辙预估模型

李伊梁，魏建国，李佳桐，付其林

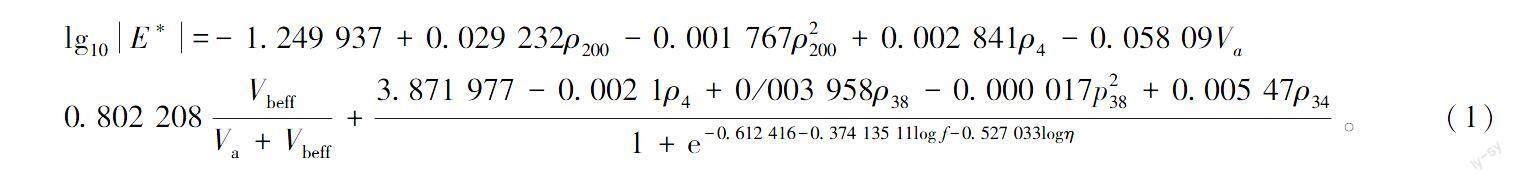
摘要：为建立分层变模量下沥青路 面车辙预估模型，修正动态模量变化引起沥青路面永久变形预估的偏差。根据沥青混合料动态模量试验和室内三轴动态蠕变试验，验证沥青混合料动态模量（| E* |）与其抗高温变形能力的相关性；采用Abaqus有限元软件分析不同时间沥青路面随深度、温度的动态模量和竖向压应力变化规律，提出各亚层在不同动态模量下的竖向压应力修正因子（m）；根据“亚层变形叠加”思想，运用SPSS软件回归分析，建立包含温度、沥青层厚度、竖向压应力、修正因子和荷载作用次数等因素的分层变模量沥青路面车辙预估模型。结果表明，建立的车辙预估模型可更为准确地预估沥青路面的永久变形，可将中、下面层车辙预估精度分别提高6.03%和10.34%，沥青层整体提高5.19%。

关键词：道路工程；车辙预估模型；有限元；变模量；沥青路面

中图分类号：U414文献标识码：A文章编号：1006-8023（2024）01-0183-08

Rutting Prediction Model of Asphalt Pavement Under Layered Variable Modulus

LI Yiliang， WEI Jianguo*， LI Jiatong， FU Qilin

（School of Traffic & Transportation Engineering， Changsha University of Science and Technology， Changsha 410004， China）

Abstract：To establish the rutting prediction model of asphalt pavement under layered variable modulus， the deviation of permanent deformation prediction of asphalt pavement caused by dynamic modulus change was corrected. Based on the asphalt mixture dynamic modulus test and laboratory triaxial dynamic creep test， the correlation between the asphalt mixture dynamic modulus （| E* |） and its high-temperature deformation resistance was verified. Abaqus finite element software was used to analyze the dynamic modulus and vertical compressive stress of asphalt pavement with depth and temperature at different times， and the correction factor （m） of vertical compressive stress of each sub layer under different dynamic modulus was proposed. According to the idea of ｀ sub layer deformation superposition'， a rutting prediction model of layered variable modulus asphalt pavement was established by using SPSS software regression analysis， which included temperature， asphalt layer thickness， vertical compressive stress， correction factor， load action times and other factors. The results showed that the established rutting prediction model can more accurately predict the permanent deformation of asphalt pavement， improve the rutting prediction accuracy of middle and lower layers by 6.03% and 10.34%， respectively， and improve the overall asphalt layer by 5.19%.

Keywords：Road engineering; rutting prediction model; finite element; variable modulus; asphalt pavement

0引言

車辙作为沥青路面永久变形，是影响沥青路面质量和服役寿命最严重的破坏形式之一[1-2]。沥青路面车辙的产生和发展与路面温度[3-4]、动态模量指标[5-6]、荷载应力[7]的分布密切相关，但在众多车辙预估模型和室内试验中，路面温度场和应力场通常被作为重要考虑因素，而模量场大多基于20 ℃时的动态模量指标，但沥青路面模量场在外界环境影响下处于波动状态，这导致不考虑动态模量变化所建立的沥青路面车辙预估模型存在一定的局限性。

为了体现动态模量对路面车辙的影响，陈岳峰[8]通过计算标准车速下沥青路面不同层的动态模量，发现在温度影响下动态模量发生大幅变化，从而显著影响沥青路面高温性能；胡贵华等[9]将温度梯度和动态模量引入车辙预估模型，提出了多温度梯度下的车辙预估方法，但该模型在进行路面车辙预估时，须对选定路面结构和各层混合料分别进行多因素水平下的全厚式车辙试验和动态模量试验，从而确定车辙预估模型各因子影响系数，该方法过程繁琐且未运用大量试验数据对模型进行修正，预估精度难以保证；谢来斌[10]从室内车辙试验及试验条件出发，结合有限元数值模拟，建立了考虑温度与动态模量等因素的车辙预估模型，但该模型仅对SMA-13的预估有效性进行了验证，且缺乏修正；杨永红等[11]通过三层车辙试验，建立了包含沥青层厚度、荷载作用和动态模量指标等因素的不同温度区间下的车辙深度预估模型，但该模型在修正时仅考虑了20～40 ℃的温度区间，导致更高温度下车辙预估精度仍存在较大偏差。可见，目前基于室内试验和有限元软件所建立的车辙预估模型，在反映动态模量随温度和深度变化对路面车辙变形影响方面依然存在不足，预估效果仍具有一定的局限性。

为了修正动态模量变化引起沥青路面车辙预估的偏差，本研究首先通过沥青混合料动态模量试验和三轴动态蠕变试验结果，验证了动态模量与车辙变形之间的相关性；然后采用Abaqus有限元软件分析长沙地区中高温月份不同时间沥青路面随深度和温度的动态模量与竖向压应力变化规律，并提出竖向压应力修正因子m；最后，结合室内标准车辙试验数据，采用“亚层变形叠加”思想，运用SPSS软件回归分析，建立包含温度、沥青层厚度、竖向压应力、修正因子和荷载作用次数等因素的分层变模量沥青路面车辙预估模型，并对模型参数进行修正和模型的有效性验证。

1动态模量与车辙变形量相关性验证

为验证动态模量与沥青混合料高温抗永久变形能力的关系，美国LTPP计划对不同路段车辙变形量监测并钻芯取样进行动态模量试验，证实了动态模量可以作为沥青混合料抗高温变形能力的评价指标。本研究对3种沥青混合料AC-13、AC-20和AC-25进行不同温度下动态模量试验和三轴动态蠕变试验，蠕变试验设置围压10 kPa，半正弦波加载，每次加载0.2 s，卸载0.8 s，共加载3 600次。试验结果如图1所示。

由图1可知，随温度升高，同一沥青混合料动态模量降低，抗永久变形能力下降，表明沥青混合料的动态模量能有效反映其抗高温车辙性能，可作为沥青混合料抗永久变形能力预估和评价的指标。

2沥青面层有限元模型构建与各亚层动态模量确定

2.1路面有限元计算模型及参数

2.1.1计算模型

基于Abaqus软件建立了宽3.75 m、高3.1 m的沥青路面二维结构模型，模型共划分为6层，其几何结构图模型如图2所示，单元格划分如图3所示。

2.1.2材料参数

1）黏弹性参数

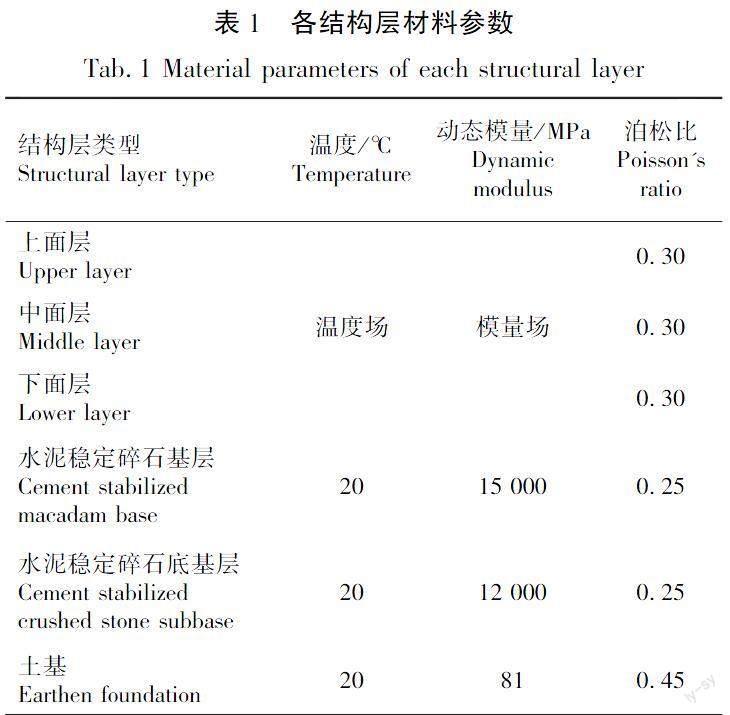
沥青层温度场和模量场采用各月份代表时刻有限元模拟结果；基层和土基在温度和应力下变形可忽略不计，其弹性参数参考现行规范，以20 ℃为标准条件，得到各结构层材料黏弹性参数见表1。

2）体积参数

通过沥青混合料原材料试验、级配设计和最佳油石比的确定，获取3种沥青混合料动态模量预估模型所需的体积参数，结果见表2。

3）气象参数

综合考虑长沙地区交通量、气象资料，将长沙地区高温月份（5—10月份）气象参数作为参考，气象资料见表3。

2.1.3热物性参数

在进行有限元分析时，可将材料热物性参数设为定值。通过查阅相关资料[12]，各结构层材料厚度及热物性能参数取值见表4。

2.1.4应力计算参数

1）力学响应指标

提取有限元结果可以得到竖向拉应力、竖向压应力和剪应力等力学响应指标，以竖向压应力作为主要分析指标。

2）计算点位确定

根据《公路沥青路面设计规范》JTG D50—2017对比沥青路面在不同水平层位的应力响应结果，将应力分析值最大的点位视为计算点位。

2.2沥青面层各亚层动态模量确定

根据涂义鹏[13]建立长沙地区中高温月份温度场模型的基本方法，将本研究中的材料参数和气象

参数代入有限元路面结构模型，建立符合本研究的温度场模型。在温度场的基础上，根据马翔等[14]修正后的NCHRPI-37A动态模量预估模型进行路面动态模量场预估，计算模型见式（1）；各亚层沥青黏度根据式（2）计算，回归截距和黏度的温度敏感性取值参考白琦峰等[15-16]研究结果。

lg10E*=－1.249 937+0.029 232ρ200－0.001 767ρ2200+0.002 841ρ4－0.058 09Va

0.802 208VbeffVa+Vbeff+3.871 977－0.002 1ρ4+0/003 958ρ38－0.000 017p238+0.005 47ρ341+e－0.612 416－0.374 135 11log f－0.527 033logη 。（1）

lglg（η×103）=A+VTS·lgTR。（2）

式中：E*为动态模量；η为黏度，Pa·s，按式（2）计算；f为荷载频率，Hz；Va为空隙率，%；Vbeff为沥青体积率，%；ρ34、ρ38、ρ4为19.0、9.5、4.75 mm筛孔累积筛余百分率；ρ200为通过0.075 mm筛的百分数；A为回归截距；VTS为黏度的温度敏感性回归斜率；TR为各亚层中间位置兰式温度，°R。

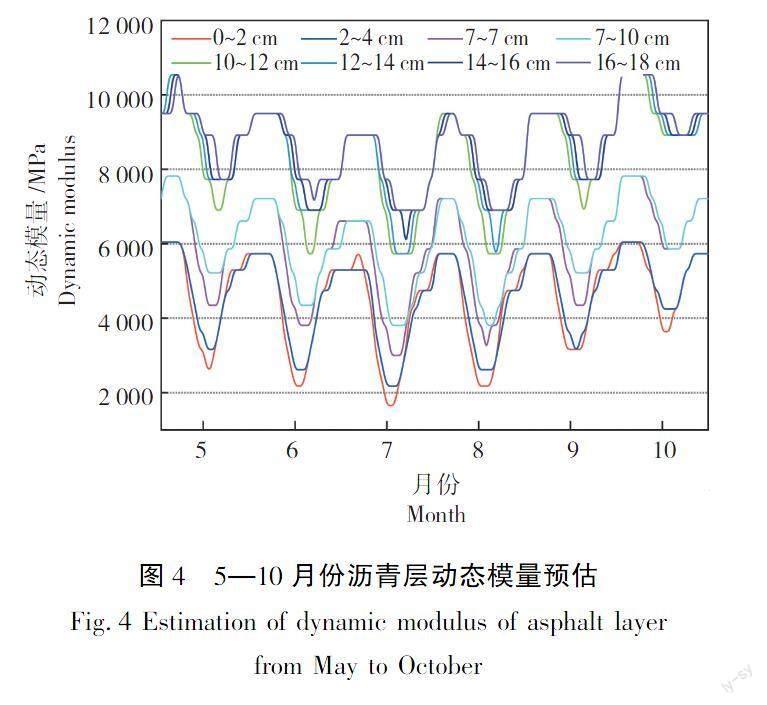
根据表2中沥青混合料体积参数，采用10 Hz的荷载频率，计算得到不同温度下3种混合料AC-13、AC-20、AC-25的动态模量代表值，见表5。然后将沥青层划分为8个层位，各层位深度分别为0～2、2～4 、4～7、7～10 、10～12 、12～14 、14～16、16～18 cm，各层温度以层顶和层底的温度平均值来表示，各层在不同时刻的温度数据从小到大以5 ℃为跨度划分为9个温度区间（17.5 ～22.5）、（22.5 ～27.5）、…、（57.5 ～62.5） ℃；最后，在Abaqus软件中将各层沥青混合料在不同温度下的动态模量代表值代入相应时刻的温度区间，以该温度区间中值所对应的动态模量作为预估结果，得到长沙地区5—10月各月份不同代表时刻的动态模量预估结果，如图4所示。

由图4可知，当温度较低时，各层沥青混合料动态模量较大；当温度较高時，各层沥青混合料动态模量较小；受路面内部温度变化趋势影响，上面层动态模量变化的幅度最大，中面层次之，下面层最小。

3沥青面层各亚层竖向压应力预估与修正因子提出

3.1竖向压应力预估

根据《公路沥青路面设计规范》（JTG D50—2017），在有限元模型中按要求施加相应大小的荷载；参考张争奇等[17]研究结果，取荷载单轮圆距离21.3 cm，两轮中心距31.95 cm，接地长度19.2 cm。

根据图4动态模量预估结果，将长沙地区全年温度较高的7月份24个代表时刻的动态模量场数据依次导入路面有限元模型中，通过模拟计算和数据分析，得到7月份沥青路面在不同时刻各层位的竖向压应力变化规律，结果如图5所示。

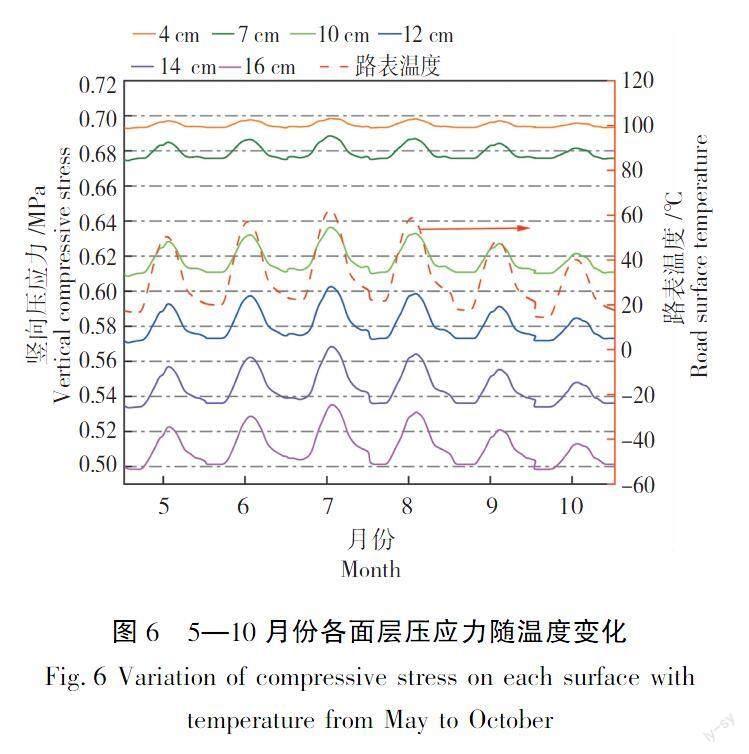
由图5可知，临近地表2 cm内的沥青混合料层顶竖向压应力几乎不受温度和动态模量变化的影响，而中下面层的竖向压应力随时间呈现出明显的起伏变化。这是由于当温度较低时，各层沥青混合料动态模量较大，竖向压应力沿路面深度方向不断扩散，不断递减；当温度较高时，上面层沥青混合料动态模量大幅度降低，导致上面层对竖向压应力的消减能力减弱，而中、下面层则需承受更大的竖向压应力。因此，将中、下面层中高温月份代表时刻动态模量场数据分别导入有限元软件中，得到中高温月份竖向压应力模拟结果如图6所示。

由图6可知，中高温月份沥青层不同层位竖向压应力随时间变化趋势具有相似性，且与路表温度的变化紧密相关。当路表温度较高时，中、下面层各层位竖向压应力较大，当路表温度较低时，中、下面层各层位竖向压应力相应较小，且由于不同月份之间温度场和模量场的差异，各层位竖向压应力的极值也会有所不同。

3.2修正因子提出

为体现在动态模量影响下各层位竖向压应力的变化特征，本研究将路表温度作为自变量，以20 ℃时各层位竖向压应力（p）与实际动态模量影响下各层位竖向压应力（pm）的比值作为修正因子m，即竖向压应力修正因子m=p/pm。通过对中高温月份不同时刻的沥青路面中、下面层各层位竖向压应力修正因子m进行统计整理，得到1 008个數据，采用SPSS软件对各层位竖向压应力修正因子与路表温度之间的关系进行回归分析，得到各层位修正因子计算式，见表6。

4车辙预估模型建立与评价

4.1建立车辙预估模型

基于力学经验法和鲁正兰等[18]、Liu等[19]研究结论，在车辙预估模型中用幂函数的形式将沥青层厚度、竖向压应力和轮载作用次数等主要因素引入，根据“亚层变形叠加”原理提出车辙预估模型，见式（3）—式（5）。

Ra=∑ni=1Rai 。（3）

Rai=F（T，pi，N，hiho，R0i） 。（4）

Rai=kTapbNc（hih0）R0i 。（5）

式中：Ra为沥青混合料层总的永久变形，mm；Rai为第i分层永久变形量，mm；T为沥青层温度，℃；pi为第i分层竖向压应力，MPa；N为荷载作用次数，次；hi为第i分层厚度，mm；h0为蠕变试验试件厚度，100 mm；R0i为第i分层沥青混合料在标准试验条件下加载1 h的永久变形量车辙深度，mm；hi为各亚层厚度，mm；k为回归系数；a为温度系数指数；b为应力系数指数；c为荷载作用次数指数。

通过实测3种沥青混合料（AC-13、AC-20、AC-25）在400、800、1 200…3 600次的永久变形数据，运用SPSS软件对所测永久变形数据进行多元非线性拟合，得到式（5）中a、b、c的值。在约掉各亚层厚度后，将R0移至方程左端，对方程两端取对数，利用线性拟合手段解决非线性拟合问题。拟合后R2为0.889，F检验通过，得到预估模型式（6）

Rai=9.141×10－8T3.319pi1.52N0.435hih0R0i。（6）

为充分考虑沥青路面各亚层动态模量对车辙预估模型的影响，将竖向压应力修正因子m引入式（6），得到分层变模量下的沥青路面车辙预估模型式（7）

Rai=9.141×10-8T3.319（pim）1.52N0.435（hih0）R0i。（7）

4.2车辙预估模型评价

采用相同条件分别对沥青路面永久变形进行预估和实测，比较实测值与预估值之间的偏差，以对本研究所建立的车辙预估模型准确性进行评价。

1）车辙预估模型计算参数

选用与前文中有限元模型一致的路面结构，层位划分和计算参数见表7。

预估模型中温度条件选用2020.8.8.14：00时刻温度场数据，取各亚层顶部和底部温度平均值为该亚层温度代表值，荷载大小为0.7 MPa，荷载作用次数为3 600次，各层竖向压应力修正因子m根据表6计算。

2）室内试验

采用蠕变试验对预估结果进行对比验证，蠕变试验试件为2 cm厚AC-13、3 cm厚AC-20、4 cm厚AC-25。以有限元模型中提取的14：00时刻的竖向压应力作为荷载大小，其他试验条件与预估过程中各条条件保持一致，具体方案如图7所示。

3）预估值与实测值对比

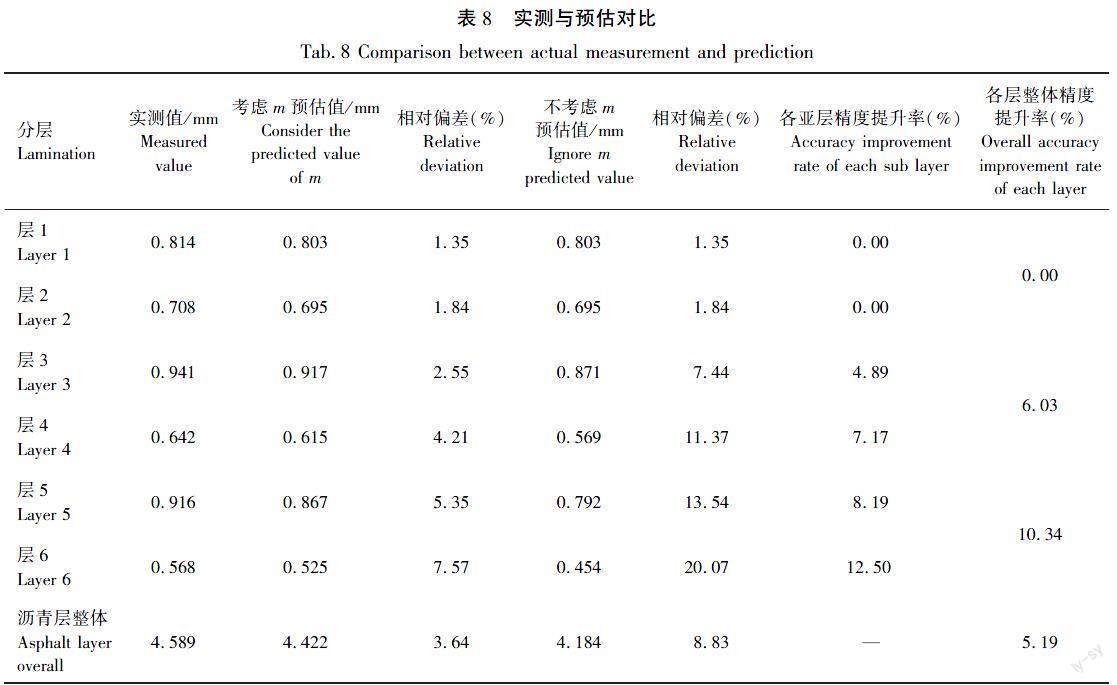
采用考虑竖向压应力修正因子和不考虑竖向压应力修正因子的2种预估模型进行车辙预估，并与实测值对比评价2种模型的有效性，实测数据及2种预估值的对比结果见表8。

由表8可知，当N=3 600时，中面层预估偏差由修正前的9.40%降低至3.38%，预估精度提升6.03%；对于下面层，预估偏差由修正前的16.80%降低至6.46%，预估精度提升10.34%；对于沥青层整体，预估偏差由修正前的8.83%降低至3.64%，预估精度提升5.19%。可见，在引入竖向压应力修正因子m后，车辙预估模型准确性得到进一步提升，且下面层预估精度提升尤为显著。

5结论

1）根据对长沙地区中高温月份沥青路面随深度、温度的动态模量场和应力场预估，发现在路面温度影响下上面层动态模量变化幅度最大，中面层次之，下面层最小；路表温度越高，中、下面层竖向压应力越大，路表温度越低，中、下面层竖向压应力相应越小；上面层竖向压应力几乎不受路表温度影响。

2）根据“亚层变形叠加”思想对路面结构进行分层，提出了各亚层在不同动态模量下的竖向压应力修正因子m；在车辙预估模型中引入温度、沥青层厚度、荷载作用次数、竖向压应力及修正因子m等重要因素，建立了分层变模量下的沥青路面车辙预估模型，该模型可在一定程度上反映沥青路面结构的车辙变形特性。

3）根据室内蠕变试验对修正后的车辙预估模型进行数据验证，结果表明采用分层变模量下车辙预估模型可将中面层、下面层预估精度分别提升6.03%和10.34%，沥青层整体预估精度可提升5.19%。可见，竖向压应力修正因子m的引入可显著提高车辙预估模型精度。

【参考文献】

[1]李喜，王选仓，房娜仁，等.基于温度与荷载实际耦合的沥青路面车辙预估[J].长安大学学报（自然科学版），2018，38（5）：67-75.

LI X， WANG X C， FANG N R， et al. Rutting prediction of asphalt pavement based on actual coupling of temperature and load[J]. Journal of Chang'an University （Natural Science Edition）， 2018， 38（5）： 67-75.

[2]赵碧全，冉武平，王亚强.基面层间接触状态对沥青路面车辙影响的室内试验分析[J].公路工程，2023，48（4）：64-69，133.

ZHAO B Q， RAN W P， WANG Y Q. Laboratory test analysis of influence of contact state between base layer on rutting of asphalt pavement[J]. Highway Engineering， 2023， 48（4）： 64-69， 133.

[3]李伊，劉黎萍，孙立军.沥青面层不同深度车辙等效温度预估模型[J].吉林大学学报（工学版），2018，48（6）：1703-1711.

LI Y， LIU L P， SUN L J. Prediction model on rutting equivalent temperature for asphalt pavement at different depth[J]. Journal of Jilin University （Engineering and Technology Edition）， 2018， 48（6）： 1703-1711.

[4]吁新华，谈至明，胡洪龙，等.沥青面层的车辙等效温度[J].同济大学学报（自然科学版），2014，42（5）：701-706，729.

YU X H， TAN Z M， HU H L， et al. Rutting equivalent temperature for asphalt pavement[J]. Journal of Tongji University （Natural Science）， 2014， 42（5）： 701-706， 729.

[5]陈改霞，尹艳平，罗要飞.玄武岩纤维对钢渣沥青混合料性能影响研究[J].硅酸盐通报，2022，41（2）：657-666.

CHEN G X， YIN Y P， LUO Y F. Effect of basalt fiber on performance of steelslag-asphalt mixture[J]. Bulletin of the Chinese Ceramic Society， 2022， 41（2）： 657-666.

[6]刘红，孔永健，曹东伟.加入聚酯纤维对沥青混合料动态模量的影响[J].公路交通科技，2011，28（8）：25-29，45.

LIU H， KONG Y J， CAO D W. Influence of adding polyester fiber on dynamic modulus of asphalt mixture[J]. Journal of Highway and Transportation Research and Development， 2011， 28（8）： 25-29， 45.

[7]高语，滕旭秋.基于COMSOL的沥青混凝土路面车辙预估[J].河北大学学报（自然科学版），2020，40（6）：578-584，646.

GAO Y， TENG X Q. Rutting prediction of asphalt concrete pavement based on COMSOL[J]. Journal of Hebei University （Natural Science Edition）， 2020， 40（6）： 578-584， 646.

[8]陈岳峰.基于MEPDG的组合式基层沥青路面车辙预估[J].公路交通科技，2020，37（12）：15-23.

CHEN Y F. Predictingrut of composite base asphalt pavement based on MEPDG[J]. Journal of Highway and Transportation Research and Development， 2020， 37（12）： 15-23.

[9]胡贵华，李彦伟，张倩，等.考虑温度梯度和动态模量的全厚式车辙深度预估[J].长安大学学报（自然科学版），2015，35（3）：8-12，20.

HU G H， LI Y W， ZHANG Q， et al. Depth prediction of total thickness rutting considering temperature gradient and dynamic modulus[J]. Journal of Chang'an University （Natural Science Edition）， 2015， 35（3）： 8-12， 20.

[10]谢来斌.基于温度场和动态模量的沥青混合料车辙预估模型研究[D].西安：西安建筑科技大学，2013.

XIE L B. Research of asphalt pavement rutting prediction model based on temperature filed and dynamic modulus[D]. Xi'an： Xi'an University of Architecture and Technology， 2013.

[11]杨永红，张尚龙，张倩.基于动态模量和三层式车辙试验的车辙深度预估[J].西安建筑科技大学学报（自然科学版），2019，51（5）：717-723，762.

YANG Y H， ZHANG S L， ZHANG Q. Rutting depth prediction based on dynamic modulus and three-layer wheel track rutting test[J]. Journal of Xi'an University of Architecture & Technology （Natural Science Edition）， 2019， 51（5）： 717-723， 762.

[12]廖公云，黃晓明.ABAQUS有限元软件在道路工程中的应用[M].南京：东南大学出版社，2008.

LIAO G Y， HUANG X M. Application of ABAQUS finite element software in road engineering[M]. Nanjing： Southeast University Press， 2008.

[13]涂义鹏.考虑温度场的沥青路面车辙变化特征分析研究[D].长沙：长沙理工大学，2014.

TU Y P. The analysis of rutting variation of asphalt pavement considered temperature field[D]. Changsha： Changsha University of Science & Technology， 2014.

[14]马翔，倪富健，陈荣生.沥青混合料动态模量试验及模型预估[J].中国公路学报，2008，21（3）：35-39，52.

MA X， NI F J， CHEN R S. Dynamic modulus test of asphalt mixture and prediction model[J]. China Journal of Highway and Transport， 2008， 21（3）： 35-39， 52.

[15]白琦峰.沥青路面力学经验法车辙预估研究[D].南京：东南大学，2013.

BAI Q F. Study on rutting prediction of asphalt pavement mechanics by empirical method[D]. Nanjing： Southeast University， 2013.

[16]白琦峰，钱振东，李浩天，等.基于统计回归法的沥青路面温度场模型[J].公路交通科技，2011，28（11）：27-31.

BAI Q F， QIAN Z D， LI H T， et al. Asphalt pavement temperature field model based on statistic regression method[J]. Journal of Highway and Transportation Research and Development， 2011， 28（11）： 27-31.

[17]张争奇，罗要飞，雷宗建.箱梁结构参数对铺装结构受力的影响分析[J].公路，2013，58（8）：149-155.

ZHANG ZQ， LUO Y F， LEI Z J. Influence of box girder structural parameters on mechanistic performance of pavement structure[J]. Highway， 2013， 58（8）： 149-155.

[18]鲁正兰，孙立军.沥青路面车辙预估方法的研究[J].同济大学学报（自然科学版），2007，35（11）：1476-1480.

LU Z L， SUN L J. Research on rutting prediction of asphaltpavement[J]. Journal of Tongji University （Natural Science）， 2007， 35（11）： 1476-1480.

[19]LIU G， CHEN L L， QIAN Z D， et al. Rutting influencing factors and prediction model for asphalt pavements based on the factor analysis method[J]. Journal of Southeast University （English Edition）， 2021， 37（4）： 421-428.