基于车流波动理论的匝道达到控制与仿真效果评价

康诚，潘新福，严欣，范欣炜

摘要：以匝道达到控制为主体的合流区主动交通管控是高速公路与城市快速路在提升交织区通行能力与交通安全采用的重要方法。采用历史真实交通数据，结合优化的速度波动理论模型，构建车辆在拥挤流交织过程中的运行状态模型，量化分析混合控制决策下最优化的管控方案，并通过优化的仿真平台，获取车辆轨迹、分布及冲突状况等信息，验证结论的实际效果。以秦洪立交为例进行模型试验论证，对比匝道单一控制与匝道主线混合控制的优化效果。结果表明，相对于无管控状态，单一匝道控制下冲突减少52.5%，但车辆延误增长20.5%；混合控制下冲突减少68.1%，且车辆延误降低12.0%。由此可知控制模型对匝道交通安全与效率有明显优化效果。其中，采用匝道主线混合控制时效果最佳，有效提升匝道通行效率和交通安全效益。

关键词：车流波动理论；交通组织；入口匝道控制；交通仿真；交通安全评价

中图分类号：U491文献标识码：A文章编号：1006-8023（2024）01-0191-10

Ramp Metering and Simulation Effect Evaluation Based on Traffic Fluctuation Theory

KANG Cheng， PAN Xinfu， YAN Xin， FAN Xinwei

（CATARC Automotive Proving Ground Co.， Ltd.， Yancheng 224100， China）

Abstract：The active traffic control in the merging area， which takes ramp arrival control as the main body， is the main means adopted by the expressway and urban expressway to improve the capacity and traffic safety of the weaving area. In this study， the historical real traffic data and the optimized theoretical model of speed fluctuation are used to build the vehicle arrival model in the process of congestion and queue weaving， and the optimal control scheme under the mixed control decision is quantitatively analyzed. Through the optimized simulation platform， the vehicle trajectory， distribution and conflict status are obtained， and the actual effect of the conclusion is verified. This study takes Qinhong Interchange as an example to demonstrate the model test， and verify the optimization effect of ramp single control and ramp main line mixed control under the optimization effect. The results show that the conflict under ramp control is reduced by 52.5% and the vehicle delay is increased by 20.5% compared with the uncontrolled state. The conflict and vehicle delay under hybrid control are reduced by 68.1% and 12.0%， respectively. It can be seen that the control model has obvious optimization effect on ramp traffic safety and efficiency. One of the most effective control strategies is the ramp mainline mixed control， which leads to significant improvements in ramp traffic efficiency and traffic safety.

Keywords：Traffic fluctuation theory; traffic organization; on-ramp control; traffic simulation; traffic safety evaluation

0引言

當前我国城市快速路交通流量急剧增加，各种交通问题也随之出现，尤其是由匝道汇入的支线车辆与快速路主线车辆在合流区发生并道合流所形成的交织区范围内。在该路段由于强制的换道行为与交通冲突导致局部交通拥堵、匝道排队溢出以及交通事故频发，严重影响了城市快速路以及匝道上游连接道路的通行秩序和通行效率，解决入口匝道交通问题刻不容缓[1-2]。因此，本研究基于真实场景的历史交通数据，构建符合我国城市快速路交通特性的微观交通模型，基于车流波动理论，设计匝道优化控制模型系统框架，并通过仿真模型来模拟和分析所提出的控制策略在应用时可取得的效果。

目前研究的入口匝道控制方案大多是对匝道交通流进行调节控制，或采取快速路车速诱导及限速的协调控制方案，从而实现交通流量的控制和交通拥堵事故的疏散，而对快速路主线车辆的通行权则不加以控制[3-4]。同时，针对匝道控制的模型多半为单目标或者多目标的开环/闭环控制，这种单一性的控制方案无法很完美地覆盖当下匝道多车道复杂环境下的效率与安全性问题[5-6]。在以往针对匝道控制的研究过程中，Hossain[7-8]应用微观交通仿真模型分析了匝道合流过程的通行能力和饱和流量；随后，Elefteriadou等[9]应用微观交通仿真系统 MITSIMLab评估快速路的匝道控制。Lertworawanich等 [10]采用Vissim微观仿真模型研究了车辆换道行为和车辆运行轨迹对匝道交织的影响；Vieira等[11]研究了微观交通模型与交通管理策略对匝道控制影响的关系。Ngoduy等[12]基于交通流的特性，运用交通波理论研究造成拥堵的临界条件，并将其拓扑特征分解为一系列单向链路，并在此基础上研究复杂条件下的匝道交织情况。

基于上述问题，本研究充分结合城市快速路的交通现状，利用车流波动理论和交通管控策略，构建匝道控制优化模型。城市快速路入口匝道交织区交通管控策略旨在缓解交通拥堵，提高道路通行效率和安全性，目前常见的管控策略包括交通信号灯控制[15]、车道限行[16]和车辆分流[17]等。现有策略存在以下核心不足：1）策略部署约束。当前管控策略依赖于道路旁的传感器和交通信号灯等设施，仅在有限范围内布设，无法应对城市道路网络复杂的交通状况；2）管控效果不佳。往往只能缓解部分情况下的交通拥堵，无法解决交通瓶颈本质问题，且在高峰期和节假日等特殊情况下效果非常有限；3）数据支持薄弱。目前城市交通数据采集和分析的技术并未大面积投入实地使用，数据质量和实时性存在一定问题。通过研究交织区当前的交通行为与车辆轨迹发现，目前当城市快速路上的交通量趨于饱和时，车辆经常采取与前车保持较小的间距以争取在入口匝道合流区的优先通行权，而快速路车流的车头间距过小直接导致入口匝道上的车辆无法及时汇入快速路，从而导致匝道车辆拥堵及排队溢出现象频繁发生，严重扰乱了入口匝道上游相邻道路的行车秩序。城市交通系统内各元素的性能、状态及其之间的规律联系由多方面影响因素共同作用，单一的结构模型与管控方式通常难以对其进行准确详细的描述和评估分析，因此，需要从交通系统角度出发，结合道路几何特征、交通需求结构和匝道信号设置的影响机理。本研究利用路网的历史交通信息和实时采集信息，采用交通分配和最优路径理论，结合微观交通仿真验证的方法，验证了管控策略在真实交通流量下的实际效果。

1基于车流波动理论的匝道优化管控模型

1.1优化的车流波动理论

根据车流波动理论，道路上交通流量的变化会引起车流的疏密程度变化，这种变化可以理解为车流中存在的交通波。该波以速度uw稳定地朝向某一方位进行传播，反映道路交通的运行情况。当车流从高速低密状态逐渐转变为低速高密状态时，道路上的交通流可能会出现拥堵现象，形成集结波，这种现象会导致车流量速度下降。当主车道和匝道车辆在合流区域汇合形成较少车道数的车流时，交通流特性发生相应变化，可能导致该汇合区域的实际通行能力低于其设计通过能力，从而形成交通瓶颈区段，如图1所示[13-14]。

uw为集结波波速；u1为高峰时段区间平均速度；u2为平峰时段区间平均速度；k1为高峰时段车流密度；k2为平峰时段车流密度。

uw is the gathering wave velocity; u1 is the average speed during peak hours; u2 is the average velocity in the normal peak period; k1 is the density of traffic flow during peak hours; k2 is the traffic flow density during normal peak hours.

依据车流波模型，集结波波速见式（1）。

uw=u1k1－u2k2k1－k2=q1－q2k1－k2=ΔqΔk。（1）

式中：uw为集结波波速；u1为高峰时段区间平均速度；u2为平峰时段区间平均速度；q1为高峰时段流量；q2为平峰时段流量；k1为高峰时段车流密度；k2为平峰时段车流密度；Δq为高峰时段与平峰时段流量差；Δk为高峰时段与平峰时段车流密度差。

1.2匝道车流运行情况

匝道车辆的时空轨迹图如图2所示。由图2可知，当匝道交叉口信号灯为红灯时，驶入匝道的车辆均在停车线O处等候，导致集结波ω1朝向上游方向进行传播运动，断面O向后的排队长度也会不断增大。当匝道交叉口信号灯转为绿灯后，车流将以饱和流率Sr逐渐消散。断面O处消散波ω2开启朝向上游进行传播运动，而集结波ω1将以原有速度开启朝向后方进行传播，从而导致排队车辆队列进一步增长。此后，消散波将在断面O'追上集结波，排队车辆队列完全消散，后续车辆将不再需要进行排队等候。

图中O为车辆排队起始位置，即停车线；O′为车辆排队结束位置；tr为绿灯启动损耗时间；gr为正常绿灯时间；lr为车辆排队长度；ω1为集散波；ω2为消散波。

由车流波动基础理论，匝道上集结波ω1与消散波ω2的波速可以通过以下公式计算得出。

ω1=Qr/nr－0k1－kj。（2）

ω2=0－Sr/nrkj－k2。（3）

式中：Qr为入口匝道上的车流量；k1为入口匝道的到达车流密度；nr为入口匝道车道条数；kj为排队时的阻塞车流密度；Sr为入口匝道停车线处的饱和流率；k2为入口匝道停车线处车辆疏散密度。

匝道排队队列的消散时间取决于多个因素，包括车辆进入匝道的速度、匝道的长度和容量、进入匝道的车流量以及匝道出口道路的流量等。通常情况下，当匝道排队队列达到一定长度时，需要采取措施减少排队队列，避免交通堵塞和事故的发生。研究中匝道排队队列的消散时间（tr）可定义为消散波ω2追上集结波ω1所需的时间，具体计算方法如下所示。

tr=ω1（C－gr+tr）ω2－ω1。（4）

匝道最大排队长度可通过计算消散波或集结波的传播距离来确定，具体计算方法见式（5）。

lr=ω2×tr。（5）

为保证排队队列末尾的车辆能够顺利通过交叉口，匝道信号灯的绿灯时间应当被延长，以确保该车辆能够从断面O'行驶到断面O处，即

gr≥tr+lrvr。（6）

式中：gr为绿灯时间；vr为车辆在入口匝道正常行驶的速度。

此外，受限于入口匝道长度问题，为避免匝道车流排队溢出，在控制过程中应该避免出现次生匝道拥堵现象，即在交织区交通控制情况下，形成的拥堵尾部向上游传播，并覆盖了瓶颈上游的几个进、出匝道。由于拥堵区域的交通流量低于上游到达流量，出匝道流量相应下降。因此，驶往活动瓶颈上游出口的车辆也会由于交通拥堵加速了交通拥堵的空间增长。因此，匝道控制必须满足的约束条件为一个周期内的最大排队长度应不超过匝道总长（L），即：

lr≤L 。（7）

因此，在匝道控制的方式选择上，需要着重考虑匝道交织过程中的匝道参数特性与车辆行驶特性。匝道控制需要基于交通流理论来进行流量分析和预测，以确定匝道的设计参数和控制策略，基于交通仿真技术来进行交通流模拟与测试，以评估控制策略的效果和优化控制参数。由于匝道合流区主线和匝道的交通流产生交织，与封闭路段不同，匝道车辆在加速车道中不保持最小安全距离跟驰行驶，其车速也不是自由流状态或慢启状态的车速，而是在纵向行驶过程中寻找相邻内侧车道的可插车间隙。驾驶人通常与前车保持较大距离，观察主线后方车辆，减速观察后加速完成汇入，这样的驾驶行为无疑会降低加速车道车辆在合流过程中的行驶速度，盲目地换道更可能造成交通冲突。驾驶员需要根据交通信号灯和路标的指示，及时调整车速和车道，以适应交通管控措施的变化。驾驶员需要及时感知、判断和反应，以保证道路交通的安全和畅通。同时，由于匝道上车辆需要从静止状态开始加速进入高速公路，或者从高速公路上减速进入匝道，因此匝道上车辆的加速度和减速度通常比高速公路上的车辆更大。基于匝道车流与车辆行为的特性，在控制策略设计过程中，需要针对性地进行控制流量，同时提高交织区车速，寻找合适的可插车间隙并完成汇入。在此基础上，对匝道组织的控制应考虑不同的交通流状况，制定适当的控制策略。

1.3优化的匝道组织管控模型

高速公路与匝道衔接处布设信号灯的目的是控制匝道车辆高效有序驶入高速公路，有效分流匝道和合流区高速公路交通，从而提高交叉口运行效率，降低负面影响。优化匝道交通组织模型的基本原则是通过最小化交叉口各方向交通的车辆平均延误，确保其服务水平，进而达到车辆运行效率的最佳效果，通常以交叉口饱和度来体现。为确保道路交通公平性，本研究将车流在一个周期内的平均延误作为优化控制目标。

实际交通运行过程中受到多种因素的影响，并且该系统具有随机性，导致其参数可能发生波动和变化，难以避免对原有模型准确性产生负面影响。为应对不确定性，可采用鲁棒优化控制的方法，通过牺牲部分目标来构建相应的保护框架，以避免其不确定性可能带来的约束条件失效。这种方法旨在提高匝道处交通组织系统的鲁棒性，以确保在具有可变性情况下系统的稳定性和可靠性。该模型中的约束失效表明交通流的排队长度超过入口匝道的长度，导致交通容量下降和交通沖突风险增加。交通流波动具有一定的不确定性，因此在设计优化策略时，需要考虑交通流的波动，以实现有效的交通控制。

以X表示交叉口饱和度的上限，以D表示一个周期内快速路-匝道交叉口车流总延误，构建城市快速路入口匝道合流区交通组织优化模型（P1），针对总延误最低的优化目标，控制参数通过最优化函数进行求解，目标函数与条件约束见式（8）—式（17）。

minD=minDC（Qe+Qr）。（8）

s.t.ge≥te+le/ve。（9）

gr≥tr+lr/vr。（10）

lr≤L。（11）

QeSe·gr/C<X。（12）

QrSr·gr/C<X。（13）

ge≥gemin。（14）

gr≥grmin。（15）

C≥Cmin。（16）

Mmax=M′+（k+1）ξ。（17）

式中：D为一个周期内交叉口车流平均延误；D为一个周期内交叉口车流的总延误；Qe、Qr分别为快速路与匝道的车流量；C为信号控制周期值；ge、gr为快速路绿灯时间、匝道绿灯时间；te、tr为快速路、匝道绿灯启动损耗时间；le、lr为快速路、匝道车辆排队长度；ve、vr为车辆在快速路、匝道正常行驶的速度；Se、Sr为快速路、匝道的饱和流率；gemin、grmin和Cmin分别为快速路有效绿灯时间、匝道有效绿灯时间以及信号控制周期最小值；X为控制目标参数；Mmax为单次迭代最大样本数；M′为抽样数量；k为解集的鲁棒度；ξ为平衡参数。

式（12）和式（13）表明从匝道上游驶来的车辆始终需要在有效绿灯时间内通过路口，保证到达S（或S′）路段时不会遇到剩余车辆超过上一周期（否则多周期累计预留车辆会增加，较难实现目标调控效果）。式（14）—式（17）用于确保交叉口信号周期和各相位绿灯时间不低于相应最小值，避免过于频繁的信号相位转换和车辆行驶方向的反复变更，最大程度利用交叉口的時空资源，同时提升交通安全性。假定信号配时周期损失时间（包含车辆启动损失与红灯时间）为δ，基于信号控制配时原理与车流波动理论，各项参数满足式（18）。

C=ge+gr+δ。（18）

2实例验证及仿真分析

本研究以秦洪互通立交为例，运用所搭建的微观仿真模型对设计的匝道控制方案进行相应模拟，并基于间接安全评价方法对比不同设计方案下的安全指标特性，进而得到最优解。

以左转车辆（A）和直通车辆（B）为例，图3展示了安全间接分析模型（Surrogate Safety Assessment Model，SSAM）各项交通指标的计算方法。基于交通安全理论和道路冲突研究技术，通过对微观仿真平台输出的车辆轨迹数据进行一系列分析，获取车辆冲突数据、冲突的归类和分布特征。通过特定的算法和交通安全理论对提取的道路冲突数据进行相应的数理计算和统计分析，进而选取出有效指标进行后续研究分析。

2.1微观交通仿真模型建模与标定

连续型模型的仿真研究主要目的在于构建一个离散模型，以近似表达连续现象，通常采用常微分方程初值问题数值解法进行研究。仿真过程中假定仿真模型可以通过状态方程来表示仿真系统的状态，并在计算机上进行仿真。

单步法的优势在于只需提供初始状态即可进行仿真，使得计算简单便捷。但是在处理交通仿真过程中，由于其复杂性和剧烈变化，可能会导致误差积累，从而降低仿真精度。为克服欧拉法在精度方面的不足，可选择使用Runge-Kutta法。该方法

同时考虑到计算的便利性，可以通过规定步长并使用预测校正技术来进行计算，从而提高仿真的准确性，具体计算方法见式（19）和式（20）。Runge首先提出间接采用Taylor展开方法，即用几个节点上函数值（f）的线性组合来代替其导数，然后按Taylor展开，确定其系数，以期提高方法精度。

yn+1=yn+h∑Si=1 CiKi。 （19）

Ki=f（xn+aih，yn+h∑bisKs），i=1，2，…，S;a1=0。 （20）

式中：Ci为待定权因子;h为Euler法系数;S为使用的f的个数;ai、bis为参数;Ki为taylor展开子项，如式（20）所示。

在仿真模型中，基于研究对象和仿真需求等条件选择不同的数学模型。相比欧拉法等其他数值计算方法，采用龙格-库塔法可以保证仿真的高精度和精细化，同时也为仿真研究带来更大的灵活性和自由度。该方法的主要特点包括在仿真过程中，只需了解前一时刻的系统状态即可进行任意时刻的仿真计算，具有自启动能力。此外，由于计算所需条件较少，内存占用也较少；该方法对递推公式给出不同的参数，可有不同的计算方式，解不唯一，具有灵活性；该方法能够根据精度要求来改变步长的值，在每一步的计算中都采用相同的步长来计算系数即可；该方法的仿真精度仅基于步长的选择和所应用方法的阶次，便于修正。

2.2匝道主线双车道的方案一分析

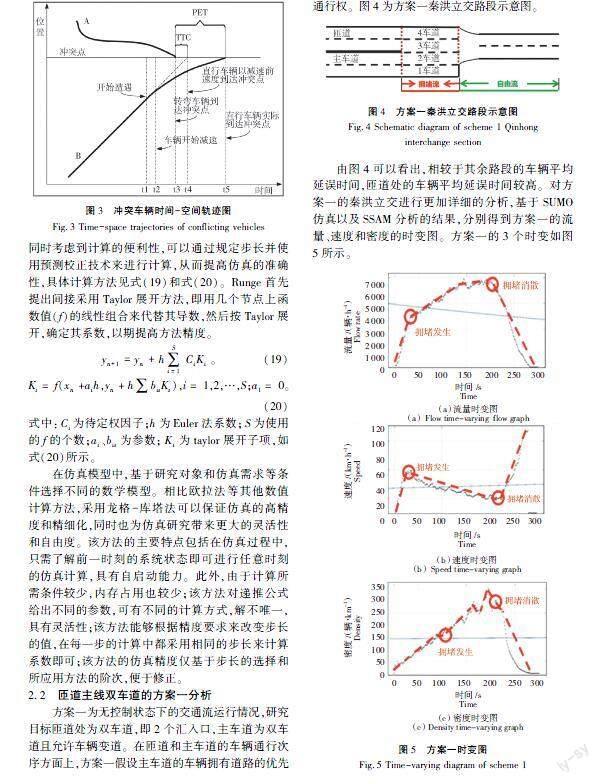
方案一为无控制状态下的交通流运行情况，研究目标匝道处为双车道，即2个汇入口，主车道为双车道且允许车辆变道。在匝道和主车道的车辆通行次序方面上，方案一假设主车道的车辆拥有道路的优先通行权。图4为方案一秦洪立交路段示意图。

由图4可以看出，相较于其余路段的车辆平均延误时间，匝道处的车辆平均延误时间较高。对方案一的秦洪立交进行更加详细的分析，基于SUMO仿真以及SSAM分析的结果，分别得到方案一的流量、速度和密度的时变图。方案一的3个时变如图5所示。

对图5中的3个时变图分析可以发现，流量在0～200 s内稳定增加，200 s之后流量开始逐渐下降；速度在0～200 s整体呈下降趋势，在225 s时陡降至18.83 km/h，在225 s之后呈上升趋势；密度在0～200 s内显著增加，在195 s时陡增至353辆/km，在200 s之后整体呈下降趋势。在获取到方案一的流量、速度以及密度时变图之后，通过SSAM软件绘制得出在方案一情况下的秦洪立交路段冲突分布图，如图6所示。

对该路段冲突分布图和时空图分析可以看出，在原现状的交通流运行情况下，即匝道处为双车道，2个汇入口，主车道处为双车道，与其他路段的车辆冲突相比，匝道处路段的车辆冲突分布较为密集。在7 200 s时，路段开始产生拥堵，1车道拥堵速度约为2 km/h，2车道的拥堵速度约为4 km/h，3车道拥堵速度约为6 km/h，4车道的拥堵速度约为12 km/h。路段由最内侧车道向右侧最外侧车道速度逐渐降低，即匝道与主线合流时，对最外侧车道的车流影响最大，最内侧的车道车流影响最小。

2.3匝道单汇入口的方案二分析

试验方案二通过限制匝道汇入车道数目试验交通流主动控制，通过试验限制匝道在交汇过程中为单车道，即单个汇入口，主车道为双车道且允许车辆变道。在匝道和主车道的车辆通行次序方面上，假设主车道的车辆拥有道路的优先通行权。图7为方案二秦洪立交路段示意图。

对方案二的秦洪立交进行详细的分析，基于微观仿真以及SSAM分析的结果，分别得到方案二的流量、速度和密度的时变图。方案二的3个时变如图8所示。

对上述3个时变图分析可以发现，流量在0～200  s内稳定增加，200  s之后流量开始逐渐下降；速度在0～50 s上升很快，在33 s时速度达到58.5 km/h，随后在33 s之后整体呈下降趋势，在225 s时陡降至14.33 km/h；密度在0～200 s内整体呈上升趋势，在225 s时为356辆/km，之后密度就呈下降趋势。在获取到方案二的流量、速度以及密度时变图之后，通过SSAM软件绘制并得出在方案二情况下的秦洪立交路段冲突分布图，如图9所示。

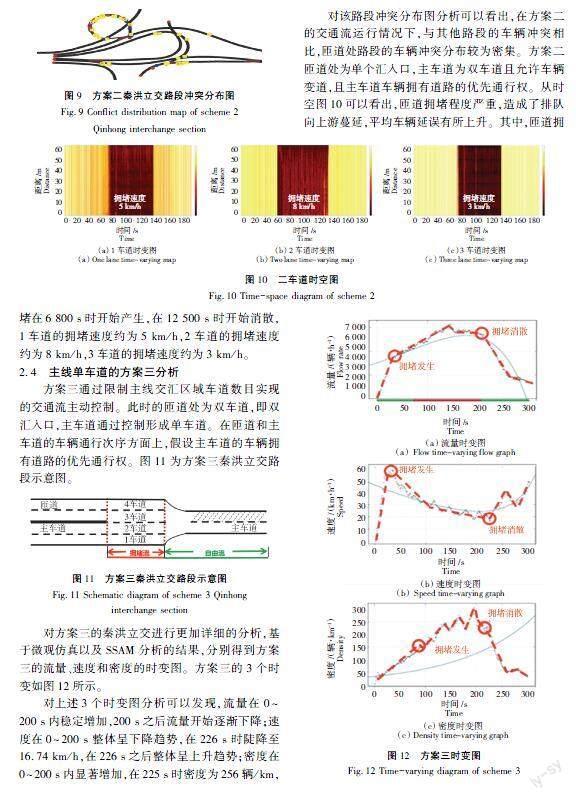
对该路段冲突分布图分析可以看出，在方案二的交通流运行情况下，与其他路段的车辆冲突相比，匝道处路段的车辆冲突分布较为密集。方案二匝道处为单个汇入口，主车道为双车道且允许车辆变道，且主车道车辆拥有道路的优先通行权。从时空图10可以看出，匝道拥堵程度严重，造成了排队向上游蔓延，平均车辆延误有所上升。其中，匝道拥

堵在6 800 s時开始产生，在12 500 s时开始消散，1车道的拥堵速度约为5 km/h，2车道的拥堵速度约为8 km/h，3车道的拥堵速度约为3 km/h。

2.4主线单车道的方案三分析

方案三通过限制主线交汇区域车道数目实现的交通流主动控制。此时的匝道处为双车道，即双汇入口，主车道通过控制形成单车道。在匝道和主车道的车辆通行次序方面上，假设主车道的车辆拥有道路的优先通行权。图11为方案三秦洪立交路段示意图。

对方案三的秦洪立交进行更加详细的分析，基于微观仿真以及SSAM分析的结果，分别得到方案三的流量、速度和密度的时变图。方案三的3个时变如图12所示。

对上述3个时变图分析可以发现，流量在0～200 s内稳定增加，200 s之后流量开始逐渐下降；速度在0～200 s整体呈下降趋势，在226 s时陡降至16.74 km/h，在226 s之后整体呈上升趋势；密度在0～200 s内显著增加，在225 s时密度为256辆/km，

在225 s之后呈下降趋势。在获取到方案三的流量、速度以及密度时变图之后，通过SSAM软件绘制得出在方案三情况下的秦洪立交路段冲突分布图，如图13所示。

对该路段冲突分布图分析可以看出，在方案三的交通流运行情况下，与其他路段的车辆冲突相比，匝道处路段的车辆冲突分布依旧较为密集。方案三匝道为双汇入口，由于该合流区长度较短，拥堵传播较快，各区间拥堵均在约3 700 s产生，在约14 500 s时开始消散。依据车流波在合流区的冲突分析，匝道车辆汇入最容易影响主线外侧车道，因此1车道速度相对较低。4车道时空图颜色较浅，拥堵发生时速度约为70 km/h，在高峰时段速度受影响较小，因此很少拥堵，匝道交通效率实现有效提升，如图14所示。

仿真并分析秦洪立交的3种设计方案，基于交叉口冲突、换道冲突以及追尾冲突，选取300 s的仿真时间，主要选用碰撞时间（Time To Collision， TTC）、后侵入时间（Post Encroachment Time， PET）和平均车辆延误（Average vehicle delay）等指标进行交通安全风险评价，得到设计方案总评价表。表1为3个方案在SSAM各个评价指标下的运行结果。

为验证优化控制模型对匝道交通安全和通行能力的提升效果，对3种设计方案的交通冲突数据进行提取采集。由表1可知，方案一为原现状的交通流运行情况；方案二为限制匝道的交通流运行情况，即将匝道的2个汇入口限制为一个汇入口；方案三为限制主线车道的交通流运行情况，即将两车道限制为单车道。相对于方案一，方案二的交通冲突数降低了52.5%，交通冲突时间增长5.9%，平均车辆延误增长20.5%。同样，相对于方案一，方案三的交通冲突降低68.1%，交通冲突时间增长17.6%，平均车辆延误降低12.0%。由此可见，方案二、三冲突数均有明显减少，优化控制模型对匝道交通安全有明显的改善效果。方案三通过设计限制主线车道的交通流运行情况，有效减少匝道交叉口处的车

辆冲突和交通拥堵，降低车辆停车等待时间，进而提高道路通行效率。交通冲突得到较好缓解，车辆延误和排队长度有所降低，有效提升了匝道交叉口处通行效率和交通安全，实现入口匝道控制优化。

3结论

本研究根据车流波动理论对入口匝道车流运行时空特性进行了分析，通过当前城市快速路的交通现状，研究了交织区在交通流量增加时的交通行为与车辆轨迹，构建了优化的车流波动模型。同时，针对现有问题提出了系统性的匝道组织管控方案。以交叉口整体车流延误最小为目标，建立了城市快速路入口匝道交叉口交通控制优化模型，分析了不同匝道控制方案条件下的交通冲突指标。在此基础上，研究以秦洪立交为例进行仿真试验，分析了基于单种管控策略与主线+匝道混合管控策略下的实际交通运行状况。根据试验结果表明，通过混合管控策略可以使匝道通行能力和交通安全得到明显改善，实现匝道控制优化，进而验证基于车流波动理论的优化模型控制效果的有效性。

【参考文献】

[1]刘兰，孙剑，李克平.城市快速路入口匝道速度控制研究[J].交通信息与安全，2011，29（3）：15-19.

LIU L， SUN J， LI K P. On-ramp speed control of urban expressway[J]. Traffic Information and Safety， 2011， 29（3）：15-19.

[2]钟连德，荣健，周荣贵，等.城市快速路与高速公路交通流特性的对比分析[J].公路交通科技，2005，22（1）：48-51.

ZHONG L， RONG J， ZHOU R G， et al. Contrasting analysis of traffic stream characteristics between urban and intercity expressways[J]. Journal of Highway and Transportation Research and Development， 2005， 22（1）： 48-51.

[3]BEN-AKIVA M， CUNEO D， HASAN M， et al. Evaluation of freeway control using a microscopic simulation laboratory[J]. Transportation Research Part C： Emerging Technologies， 2003， 11（1）：29-50.

[4]JIE L， VAN ZUYLEN H， CHEN Y， et al. Calibration of a microscopic simulation model for emission calculation[J]. Transportation Research Part C： Emerging Technologies， 2013， 31：172-184.

[5]郑进炫.基于多层统计模型的城市快速路分流区通行能力影响因素分析[J].交通与运输，2018，24（7）：72-77.

ZHENG J X. Research on influencing factors of traffic capacity in diverging area at urban expressway based on multilevel model[J]. Traffic and Transportation， 2018， 24（7）：72-77.

[6]PEL A J， BLIEMER M C J， HOOGENDOORN S P. A review on travel behaviour modelling in dynamic traffic simulation models for evacuations[J]. Transportation， 2012， 39（1）： 97-123.

[7]HOSSAIN M. Capacity estimation of traffic circles under mixed traffic conditions using micro-simulation technique[J]. Transportation Research Part A： Police and Practice， 1999， 33（1）： 47-61.

[8]HOSSAIN M. Estimation of saturation flow at signalised intersections of developing cities： A micro-simulation modelling approach[J]. Transportation Research Part A： Police and Practice， 2001， 35（2）：123-141.

[9]ELEFTERIADOU L， KONDYLI A， BRILON W， et al. Ramp metering enhancements for postponing freeway-flow breakdown[J]. Transportation Research Board Annual Meeting， 2011：348-357.

[10]LERTWORAWANICH P， ELEFTERIADOU L. A methodology for estimating capacity at ramp weaves based on gap acceptance and linear optimization[J]. Transportation Research Part B： Methodological， 2003， 37（5）：459-483.

[11]VIEIRA DA ROCHA T， CAN A， PARZANI C， et al. Are vehicle trajectories simulated by dynamic traffic models relevant for estimating fuel consumption[J]. Transportation Research Part D： Transport and Environment， 2013， 24：17-26.

[12]NGODUY D， HOOGENDOORN S P， HENK J V. Modeling and simulation of multilane and multiclass traffic flow at on and off ramps[A]. The 5th Triennial Symposium on Transportation Analysis[C].Berlin，2004：1-9.

[14]AWAD W H. Neural networks model to estimate traffic capacity for weaving segments[C]// Proceeding of the Fourth International Symposium on Uncertainty Modeling and Analysis， IEEE， 14 October 2003， College Park， MD， USA， 2003：1236144.

[15]钱国敏，凡俊生，何春光，等.智能网联混行环境下交叉口时空资源配置优化[J].浙江大学学报（工学版），2021，55（6）：1019-1026.

QIAN G M， FAN J S， HE C G， et al. Optimization of spatial-temporal resources at intersections under environment of mixed traffic flow with connected and autonomous vehicles and human-driven vehicles[J]. Journal of Zhejiang University （Engineering Science）， 2021， 55（6）：1019-1026.

[16]汪宏晨，张霞，唐炉亮，等.时段交通限行的时空动态建模与路径优化方法[J].长安大学学报（自然科学版），2017，37（5）：89-96.

WANG H C， ZHANG X， TANG L L， et al. Time and space dynamic modeling and route optimization method of time-dependent traffic restriction[J]. Journal of Chang'an University （Natural Science Edition）， 2017， 37（5）：89-96.

[17]張经纬.面向高速公路施工区的出入口匝道交通流管控研究[D].南京：东南大学，2021.

ZHANG J W. Research on traffic flow control of on-ramp ramp metering expressway construction area[D]. Nanjing： Southeast University， 2021.