可重构低熵智能车间布局建模与优化
2024-01-18郎一丁卓德城张文珠易文超
陈 勇,林 罕,郎一丁,卓德城,张文珠,易文超,裴 植
(1.浙江工业大学 机械工程学院,浙江 杭州 310023;2.宁波富佳实业股份有限公司,浙江 宁波 315000)
随着国际化的推进,企业之间的竞争愈演愈烈,订单的波动日益加剧,客户个性化需求逐渐增强。因此,在生产计划和设备工艺等领域,企业的生产过程向多样性和多变动性发展,对车间布局柔性、鲁棒性和低熵化等需求日趋增长。同时,随着工业4.0以及新兴技术的不断发展,传统车间逐渐转变为面向未来的智能车间[1]。针对这类智能车间,提出一种可重构低熵智能车间布局,企业可以在不增加车间生产面积的前提下满足更多的生产需求,在提高生产效率的同时,能够缩短企业生产周期、增加生产效益。
现有关于可重构低熵智能车间布局建模的研究较少,研究者们大多针对不确定性和多目标车间布局建模进行研究。丁穗庭等[2]详细定义了可重构度和重构成本的概念,在求解目标函数时,成功建立可重构车间背景下的多目标函数求解模型,并使用启发式算法对可重构车间模型进行求解。陈思杨[3]在研究某类注塑车间的单元布局时,根据单元搭建和单元系统布局的工艺特点分别进行建模计算,以提高作业效率,同时考虑生产计划变化带来的车间布局变化。庞嘉良等[4]在研究U型生产单元过程中,在目标函数模型约束中考虑了多个约束(时间约束、空间约束和预算约束),而在求解过程中,通过模拟退火算法和蚁群算法相结合的方式,设计了混合蚁群算法求解布局方案。王东奇等[5]和曹现刚等[6]分析了遗传算法和模拟退火算法在可重构单元布局研究中的优缺点,将两种算法结合起来,提出了遗传模拟退火算法,保留了遗传算法的全局搜索能力。丁祥海[7]在研究多目标可重构设施布局方法时,引入了空间曲线来表示设备的位置,在求解可重构布局的过程中,对全局极值进行了优化,改变了个体极值选取以及帕累托解集的策略,并对粒子群优化算法进行了改进。上述研究大多将车间布局作为一个整体进行考虑,忽略了单元内布局与单元间布局的联系。而笔者采用分层的思想,对两者分别展开研究与规划,针对智能车间布局模型多变量、多约束和非线性的特点,基于精英策略和元胞概念[8-10],设计双层遗传元胞算法,以此提高求解智能车间布局的效率,并提出可重构低熵智能车间布局模型。
1 可重构低熵智能车间布局模型
1.1 可重构低熵智能车间布局模型构建
在建立布局模型时,为了减少单个厂房布局模式的复杂性,在创建可重构车间布局[11]模型时,将其区分为单元间的布置模式与单元内的布置模式两个部分。在建立单元间的布置模式时,把单元视作最小的构成元素[12]。在建立单元内的布置模式时,把设备视作最小的构成元素。可重构低熵智能车间分层布局模型的构建过程如图1所示。

图1 可重构低熵智能车间分层布局模型构建过程Fig.1 Construction process of reconfigurable low entropy intelligent workshop hierarchical layout model
1.2 可重构低熵智能车间单元间布局模型构建
1.2.1 问题描述与假设
考虑到模型的真实性和求解模型的难度等因素,提出了以下假设:1) 车间为矩形,不考虑车间高度(假设车间高度能够容纳最高设备);2) 各单元均为矩形,尺寸已提前设定;3) 各单元与车间四周相互平行;4) 单元间的物流路径与X轴和Y轴平行;5) 车间布局已经存在。
基于上述假设,把简单单元布置的问题简化为连续式布置的问题,并且满足上述约束条件时其几何模型如图2所示。图2中:L表示厂房长度;H表示厂房宽度;Xi表示单元i的横坐标;Yi表示单元i的纵坐标;Lj表示单元j的长度;Hj表示单元j的宽度;L0表示单元与车间边界X向的最小间距;H0表示单元与车间边界Y向的最小间距。
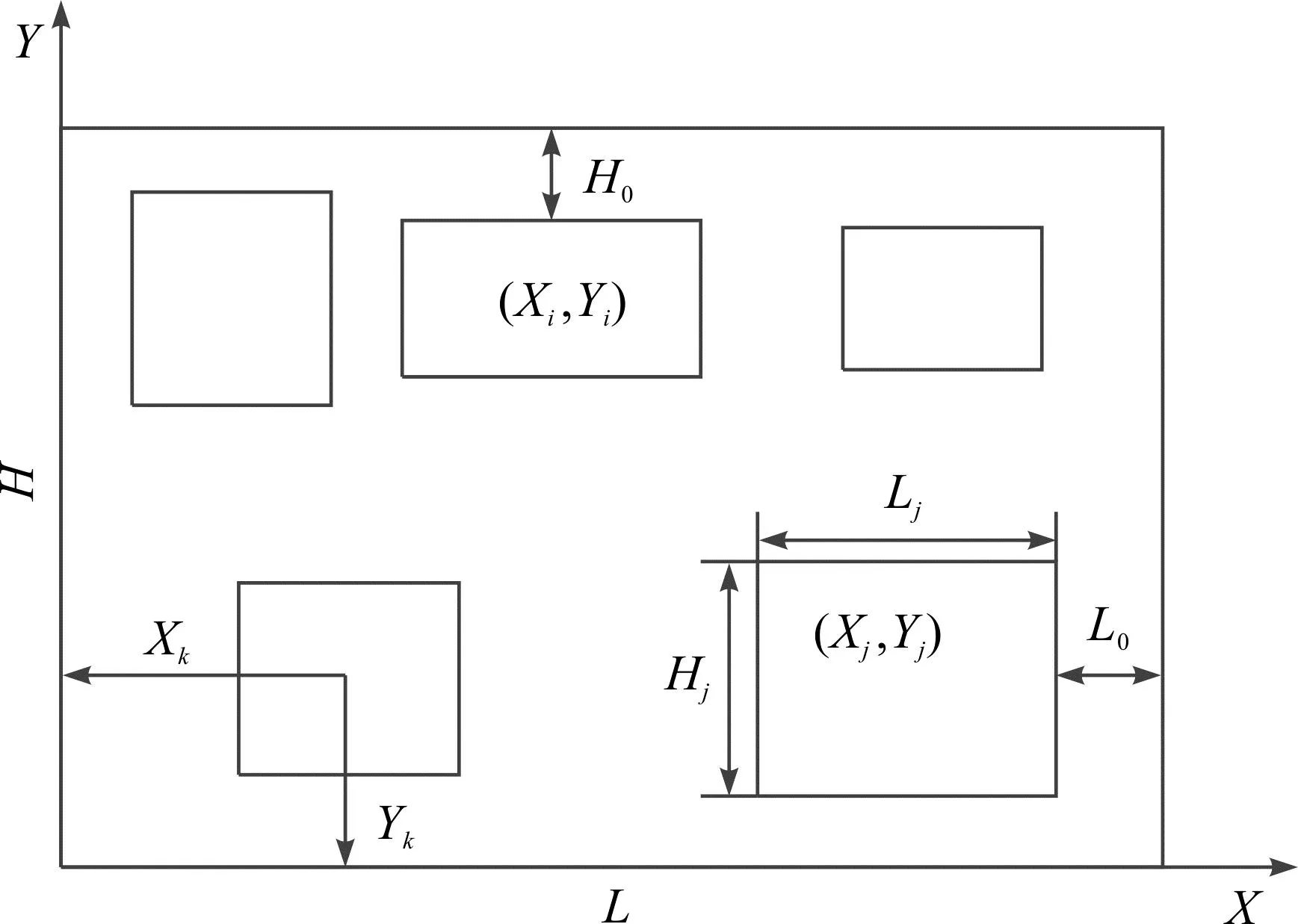
图2 单元间布局几何模型Fig.2 Geometric model of cell layout
1.2.2 面向低熵的多目标函数设计
1) 单元间物料搬运成本C1

(1)
(2)

2) 单元间单元重构成本C2
(3)
(4)

3) 单元间时间损失成本C3
(5)
(6)

4) 车间面积利用率S
为了节约土地成本,必须最大化车间面积利用率。车间面积利用率表示为
(7)
式中:Si表示每个单元的布置面积;Sl表示布局最终所占用的面积。
根据车间布局的熵理论,需要减少在制品的数量。平均在制品数量表示为
(8)
式中:R0p表示产品p在车间生产可达到的理论值;Rp表示产品p在车间生产的瓶颈值;Tp表示产品p在车间生产时的周期。
6) 柔 性V
单元间布局柔性是指增加新产品后单元间的适应性反映了车间布局的灵活性。柔性表示为
(9)

将上述6个目标函数综合处理表示为
(10)
式中:C表示成本函数;A表示单元间布局的转化柔性;Z表示给定的常值;u表示面积利用率转化成本因子,即为该车间面积占用土地总成本。
目标隶属度函数经过联立形成连续递减函数,结果如图3所示。

图3 目标隶属度函数Fig.3 Objective membership function
目标隶属度函数的表达式为
(11)
通过对模糊满意度的归一化处理,可以将基于低熵的单元间规划的多目标函数转换为单目标函数,即

(12)
1.2.3 约束条件
1) 边界约束:车间内所有单元的布置必须不能超过车间边界,即视为满足
(13)
(14)
(15)
(16)
2) 间距约束:在优化车间布局时,需要保证每个单元之间有一定的距离供人员和搬运设备的移动,即视为满足
Aij×Bij=0
(17)
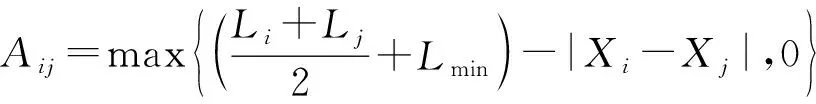
(18)

(19)
式中:Lmin表示单元在x方向的最小间距;Hmin表示单元在y方向的最小间距。
3) 固定位置约束:由于一些特殊原因,有些单元只能安排在某个区域,或者有些单元不能安排在某个区域,具体如下:
设Sk为某一特定的范围,特定范围的表达式为
(20)
某一待布置的单元i的范围pi的表达式为
(21)
由此可以推断,某个单元只能布置在特定的位置的表达式为
Pi∈Sk
(22)
而某个单元不能布置在特殊位置的表达式为
Pi∉Sk
(23)
4) 预算约束:在低熵智能车间重构过程中,单元间重构成本不能超过M0,具体表示为
C2+C3≤M0
(24)
1.3 可重构低熵智能车间单元内布局模型构建
集群内部的设备基本属于同类型,设备的大小和形状基本相同,单元和单元之间虽然没有物流关系,但和外部单元之间存在比较频繁的物流关系,通常和多个单元有物流关系。因此,结合二次分布布局模型,构建集群单元的低熵布局模型为
f=γ1[uic-u(c)]+γ2[uib-u(b)]
(25)
(26)

2 可重构低熵智能车间布局模型算法求解
2.1 基于双层遗传元胞算法的模型求解流程分析
双层遗传元胞算法以遗传算法为核心,先将精英染色体种群更换为随机产生的初始种群,再把这部分精英重新分配到元胞自动机中,使得个体遗传操作仅能和相邻结构个体进行,以达到保护种群多样性、提高算法检索能力的目的,同时避免算法“早熟”和“退化”的问题[13]。图4展示了该算法的具体求解过程。

图4 双层遗传元胞算法求解流程Fig.4 Solution flow of two-layer genetic cell algorithm
2.2 外层遗传元胞算法设计
2.2.1 精英种群引入初始种群
首先,通过遗传算法得到的最优结果即为精英染色体,再通过M次迭代生成M条精英染色体,并标记为精英染色体种群,更换其中部分随机染色体并标记为初始种群。更换过程如图5所示。

图5 精英染色体种群替换部分随机染色体示意图Fig.5 Schematic diagram of elite chromosome population replacing some random chromosomes
2.2.2 编码与解码
由于可重构低熵智能车间存在复杂的物流关系,车间单元的定位和布局方向都会影响模型目标函数,因此单元布局定位采取了整数与浮点数混合编码的方法。其中:要排列的活动单元序列号用整数部分位来表示,每个单元的坐标用浮点位表示;单元布局方向通过二进制编码(0,1),0代表单元的长度平行于X,1代表单元的长度垂直于X。以5个活动单元的编码为例,其染色体的表达如图6所示。通过使用这种编码方法,无须解码即可直接获得每个单元的具体位置。

图6 染色体编码方式Fig.6 Chromosome coding mode
2.2.3 适应度函数设计
遗传算法在优化的过程中,由于目标函数的优化和适应度函数值的增长并不相同,目标函数需要不断进行变换。笔者采用倒数构造法处理目标函数,其转换公式为
(27)
式中:fit(x)表示适应度函数;f表示目标函数。
2.2.4 选 择
轮盘赌方法用于从当前个体周围的邻居中选择两个个体。也就是说个体的适应度越高,被选择的概率就越大,概率表达式为
(28)
式中:M表示种群的个体数;fiti表示个体的适应度。根据式(28),确定概率的步骤如下:1) 求出个体的适应度;2) 每个个体的遗传概率由式(28)得出;3) 下一代个体通过轮盘赌法加以筛选。
2.2.5 交 叉
笔者使用非线性处理方法,使交叉概率随种群中个体适应值不断变化,种群更具多样性[14]。交叉概率的计算式为
(29)
式中:Pc表示交叉概率;Pc max表示交叉概率的最大值;Pc min表示交叉概率的最小值;fitbig表示执行交叉操作的两个个体相对应的适应度值中的较大值;fitmax表示当前种群中的最大适应度值;fitavg表示当前种群中的平均适应度值;λ=9.9。
在优化过程中,本研究主要涉及染色体部分,包括单元编号序列、单元坐标序列和单元布置方向序列,并使用不同的方式进行交叉。
1) 单元编号序列的交叉:两点交叉和修复程序PMX算子的结合如图7所示。

图7 单元序列的交叉Fig.7 Crossover of unit sequences

(30)
(31)
(32)
(33)
式中:e表示0~1的小数;i=1,2,…,n,n为相邻间距个数。
3) 布置方向序列的交叉:采用如图8所示的两点交叉的方式。

图8 布置方向序列的交叉Fig.8 Intersection of arrangement direction sequence
2.2.6 变 异
为了增强算法的局部随机检索能力,维持种群的多样性,笔者将引入变异算子的非线性处理方式,变异概率的计算式为
(34)
式中:Pm表示变异概率;Pm max表示最大变异概率;Pm min表示最小变异概率;fit表示执行变异操作的个体适应度值;fitmax表示当前种群最大适应度值;fitavg表示当前种群平均适应度值;λ=9.9。
在确保子代是有效解的前提下,笔者仅对单元编号序列与布置方向序列执行如图9所示的基本位变化。

图9 基本位变异法Fig.9 Basic position variation
2.3 内层遗传元胞算法设计
2.3.1 染色体编码与解码
使用自然数编码,把两倍的设备数设置成模型的染色体长度。染色体编码的前半部分表示设备和位置之间的一一对应关系;染色体编码的后半部分表示产品和设备之间的一一对应关系。
2.3.2 获得初始种群并设计适应度函数
针对流水线布局优化问题的特点,设种群规模为50,hi表示单元i宽度,用目标函数的倒数表示算法的适应度函数,即
(35)
2.3.3 选择、交叉和变异算子设定
通过选择得到适应度,因为适应度函数已知,可将蒙特卡罗法用于分配个体概率,如果个体i的适应度为fr,则选择的概率为
(36)
选择方法仍然通过轮盘赌的方式决定。适应度被转化为选择概率,轮盘被旋转,指针停留的最后位置代表被选择的个体。
因为约束条件复杂,所以选择单点交叉的方式,为了避免种群的收敛过程单一,故选用低层次的变异概率。大量的实验证明,交叉概率Pc=0.8,变异概率Pm=0.02是可以接受的。同时,根据实际应用,需要设定终止条件来停止算法进程,对流水线问题进行多次测试,最后选择进化代数Gen=100来终止算法进程。
3 可重构低熵智能车间布局算例验证分析
为了验证笔者提出的双层遗传元胞算法的有效性,引用文献中的算例对遗传算法和PSO算法进行对比验证。算法基本参数设置如下:种群数N=100,迭代数T=500,交叉概率Pc=0.7,变异概率Pm=0.01。笔者算法的仿真结果如图10所示,算法对比结果如表1所示。

表1 不同算法结果对比

图10 双层遗传元胞算法迭代过程Fig.10 Iterative process of two-layer genetic cell algorithm
由表1可知:使用双层遗传元胞算法、PSO算法和常规遗传算法均可以在有效代数内得到最优结果。对比3种算法可知:笔者双层遗传元胞算法收敛速度比其他两种算法更快,寻优时间为0.23 s,同样最优适应度值更高,最后得到的物流搬运成本最低,从而证明了双层遗传元胞算法在可重构低熵智能车间布局中的有效性和优越性。
4 可重构低熵智能车间布局实例分析
选取典型的实例,将模型算法应用到企业实际布局中,以证明算法的实用性。S公司智能车间同时实现了自动化处理、自动化搬运以及实时采集和反馈信息,其中有7个生产车间,公司以车间3为重构对象。车间3主要生产LG-2360、LCD-1.6和BD-1800。车间3长170 m,宽110 m,共14个功能单元。经计算,目前车间3物料搬运成本为2.247 8×107元,车间面积利用率为52.73%。车间3布局状况如图11所示。车间3的单元划分采用成组技术,单元划分结果如表2所示。
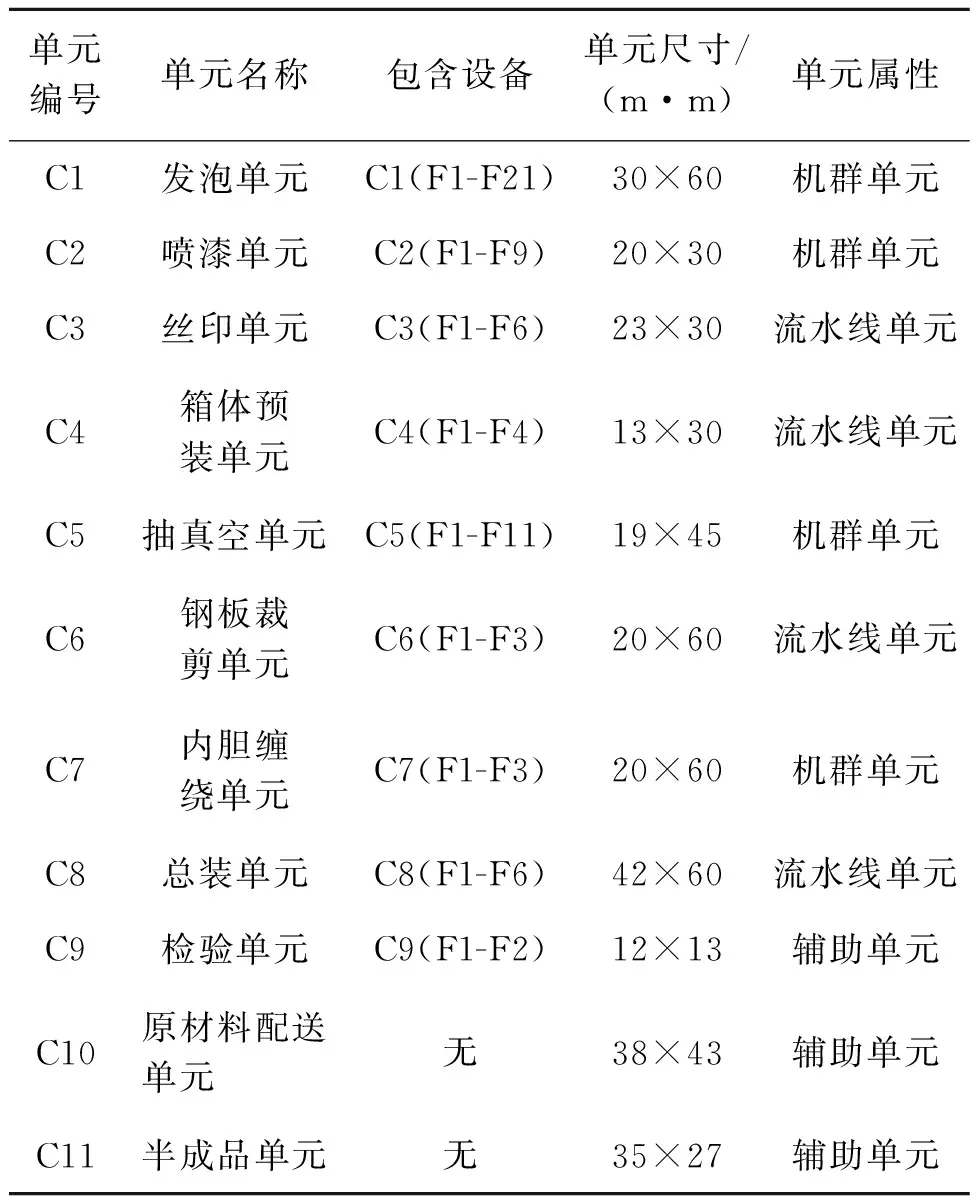
表2 单元划分结果

图11 车间3布局现状Fig.11 Layout status of workshop Ⅲ
设置双层遗传元胞算法的参数如下:设种群规模N=200、精英种群M=50,设最大迭代数T=500。文档大小K=100,反馈数目C=40,Pc max=0.8,Pc min=0.6,Pm max=0.04,Pm min=0.005。程序通过20次运算得出最优适应度函数值为2.463 3,对应的目标函数值为0.058 781。在确定各个单元的位置后,需确定各单元内部设备的布置位置,对设备较少的单元采用直观判断法,对设备较多的单元布局问题采用数学模型进行求解[15],最终选择C1,C2,C3,C4,C5,C8进行建模分析。以C1为例子,建立二次模型并运用双层遗传元胞算法对单元内设备数量、设备尺寸和单元坐标进行求解,得到布局几何模型与求解结果如图12和表3所示。将所求得的单元间布局方案与单元内布局方案相结合,得到的车间最终布局如图13所示。

表3 C1单元设备坐标表

图12 C1单元布局几何模型Fig.12 C1 unit layout geometric model

图13 车间最终布局Fig.13 Final layout of workshop
为了验证笔者提出的可重构低熵智能车间布局方法的有效性,将该方案与SLP布局方案和PSO布局方案进行比较。根据车间布局的低熵理论,低熵车间布局的指标主要包括物料搬运成本、重构成本、时间损失成本和车间面积利用率等,对比结果如图14~17和表4所示。由图17可知:笔者的布局方案通过减少物料搬运成本和设备成本,大大降低了重建成本和时间损失成本。相较于原布局,重构后的布局减少了在制品数量,使得单元内设备在生产过程中等待、停机和空转等情况减少,设备运行更加合理,设备生产能力得到有效提升。与SLP方案和PSO方案相比,笔者方案有效提高了设备的综合效率、布局灵活性和车间面积利用率。此外,优化后的布局响应企业生产过程中产品和批次的变化时具有很高的自我调节能力和适应性,产品加工的可选路径较多,路径工作效率较高,提高了低熵车间布局的抗干扰能力。可重构低熵智能车间布局建模方案具有重构时间短、响应速度快和订单输出完成率高等优点。

表4 成本指标对比

图14 评价指标对比a(uf(x))Fig.14 Comparison of evaluation indicators a(uf(x))
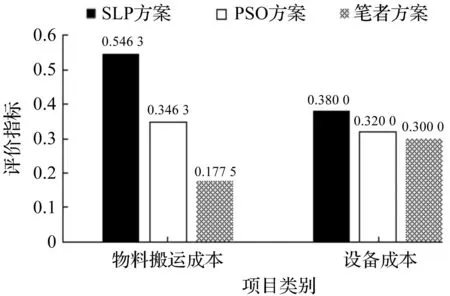
图15 评价指标对比b(1-uf(x))Fig.15 Comparison of evaluation indicators b(1-uf(x))

图16 WIP指标对比Fig.16 WIP index comparison

图17 重构成本和时间损失成本指标对比Fig.17 Comparison of reconstruction cost and time loss cost
由表4可知:SLP方案、PSO方案和笔者方案均在可重构成本M0以内,与SLP方案相比,笔者方案物料搬运成本和重构成本分别节约9.144%和42.008%;与PSO方案相比,笔者方案物料搬运成本和重构成本分别节省8.525%和22.567%。改造后的车间布局在物流上更加合理,从而降低了搬运成本,使管理更加顺畅。
综上所述,笔者提出的可重构低熵智能车间布局模型与双层遗传元胞算法是可行且有效的。将该模型和算法应用到实际车间布局过程中,可以有效地降低车间布局熵,提高布局的灵活性。
5 结 论
通过使用双层遗传元胞算法结合可重构低熵智能车间的布局概念,使得该车间模型同时具备了高柔性与高鲁棒性,并且能够在不改变车间现有面积的基础上提升车间适应产品多样性的能力,一定程度上解决了订单多变性的问题。将这一理论应用到实际场景中,并与SLP方案以及PSO方案进行对比,结果表明:笔者所提算法与模型能够更有效地实现车间低熵化,同时提高企业布局的柔性。然而笔者提出的单元内外分步建模的方法虽然降低了模型复杂度,但是提高了模型求解量。在今后的研究当中,可以考虑建立一个模型复杂程度和求解量低的多态性智能车间布局模型。
