电容失配下MAPD型级联H桥整流器纹波分析及控制
2024-01-18陶海军杨乃通王宏祎
陶海军, 杨乃通, 王宏祎
(1.河南理工大学 电气工程与自动化学院,河南 焦作 454003; 2.河南省智能装备直驱技术与控制国际联合实验室,河南 焦作 454003)
0 引 言
多电平变换器在工业应用中被广泛采用,为高压大功率问题提供了一个有效的解决方案。级联H桥整流器是一种多电平变换器,由于模块化、可扩展性的特点,得到了广泛使用[1-3]。单相级联H桥整流器(cascaded H-bridge rectifier,CHBR)系统中,固有的二次纹波功率会在直流母线衍生二次纹波电压,影响系统的性能[4]。目前,直流母线的设计通常以电解电容器为主,超大的电容可以有效地衰减单相系统固有的二次纹波功率[5]。然而,大电容的使用寿命非常有限,从功率密度以及转换效率的角度考虑,薄膜电容器具有更高的可靠性和更低的等效寄生电阻(equivalent series resistance,ESR),为改善系统的性能,使用薄膜电容的有源功率解耦(active power decoupling,APD)电路被广泛研究[6-8]。
有源功率解耦的基本概念是通过对有源电路进行适当的调制,利用电感或薄膜电容以交流形式存储系统的纹波功率,从而使交流侧和直流侧的瞬时功率达到平衡,这样可使系统可靠性增强。尽管有源功率解耦技术可以抑制系统纹波功率以及降低对直流链路电容的要求,但目前大多数功率解耦电路都需要添加额外的有源开关器件以及无源储能元件,这不仅花费了更高成本,而且增大了系统体积[9-12]。文献[13]提出了一种单模块交流分裂电容型APD拓扑,由一组附加桥臂和交流侧的分裂电容组成APD电路,由于分裂电容与交流电源相连接,不适用于多模块级联。文献[14]对直流侧降压型APD拓扑进行研究,解耦电感负责传递能量,其电感值较小,系统的功率密度有所提升。文献[15]提出了一种单模块独立式的分裂电容型解耦电路,其解耦单元并联在直流母线上,增加了额外的有源器件,提升了实施成本。文献[16]提出了一种单模块复用式直流分裂电容型有源功率解耦拓扑,可以在实现解耦功能的同时不增加开关管的数量,减少了成本及体积。本文将复用式直流分裂电容型有源功率解耦拓扑应用到单相CHBR中,所结合拓扑可应用于电力电子变压器、高压变频器等场景中。
为实现功率解耦,目前多数研究都是基于在线计算解耦电路中电容参数并进行跟踪来完成的,此方法受到解耦电路内元件参数变化的影响。文献[17]对降压型APD拓扑进行分析,对解耦电感的选取进行了优化,但解耦算法采用开环在线计算的方式,解耦精度受到元件参数变化的影响。文献[18]采用李雅普诺夫方法对解耦电容电压进行控制,获得了较高的解耦精度。文献[19]在闭环反馈解耦算法引入自适应神经模糊系统,具有在线学习的能力,能高度适应不同的情况,对系统参数的变化具有较强的鲁棒性。文献[16]针对单模块复用式分裂电容型有源功率解耦电路在电容匹配情况下提出一种双电压环控制策略,可以有效避免元件参数变化产生的影响,但在电容失配情况下该双电压环控制策略则无法有效抑制一次纹波功率。目前复用式功率解耦的相关研究均基于分裂电容匹配情况下进行的,即使是薄膜电容,随着时间及温度等影响都会发生参数漂移,所以针对复用式功率解耦拓扑研究一种适用于分裂电容失配情况下的控制策略具有重要意义。
本文主要介绍单相CHBR分裂电容型复用式有源功率解耦(multiplexed active power decoupling,MAPD)电路在电容失配下的控制方法。建立MAPD电路的数学模型,对电容失配时解耦精度降低和网侧电流衍生直流偏置和二次谐波的问题,提出一种适用于电容失配情况下的鲁棒控制策略。最后进行仿真和实验。
1 MAPD型单相CHBR拓扑及控制
1.1 分裂电容型MAPD电路拓扑及分析
单相CHBR分裂电容型MAPD电路拓扑如图1所示,其中包括单相全桥PWM整流电路和用于纹波功率补偿的MAPD电路, 和传统级联H桥整流器不同,该拓扑使用MAPD电路代替了电解电容,以第一个H桥为例,MAPD电路由开关管S13、S14以及两个解耦电容C11、C12和一个解耦电感Lf1组成,两个解耦电容Ci1和Ci2(i=1,2)串联在直流链路中,其中点通过一个滤波电感与半桥桥臂中点连接并组成解耦单元,为便于分析,假设两个解耦单元的解耦电感值相等,即Lf1=Lf2=Lf。
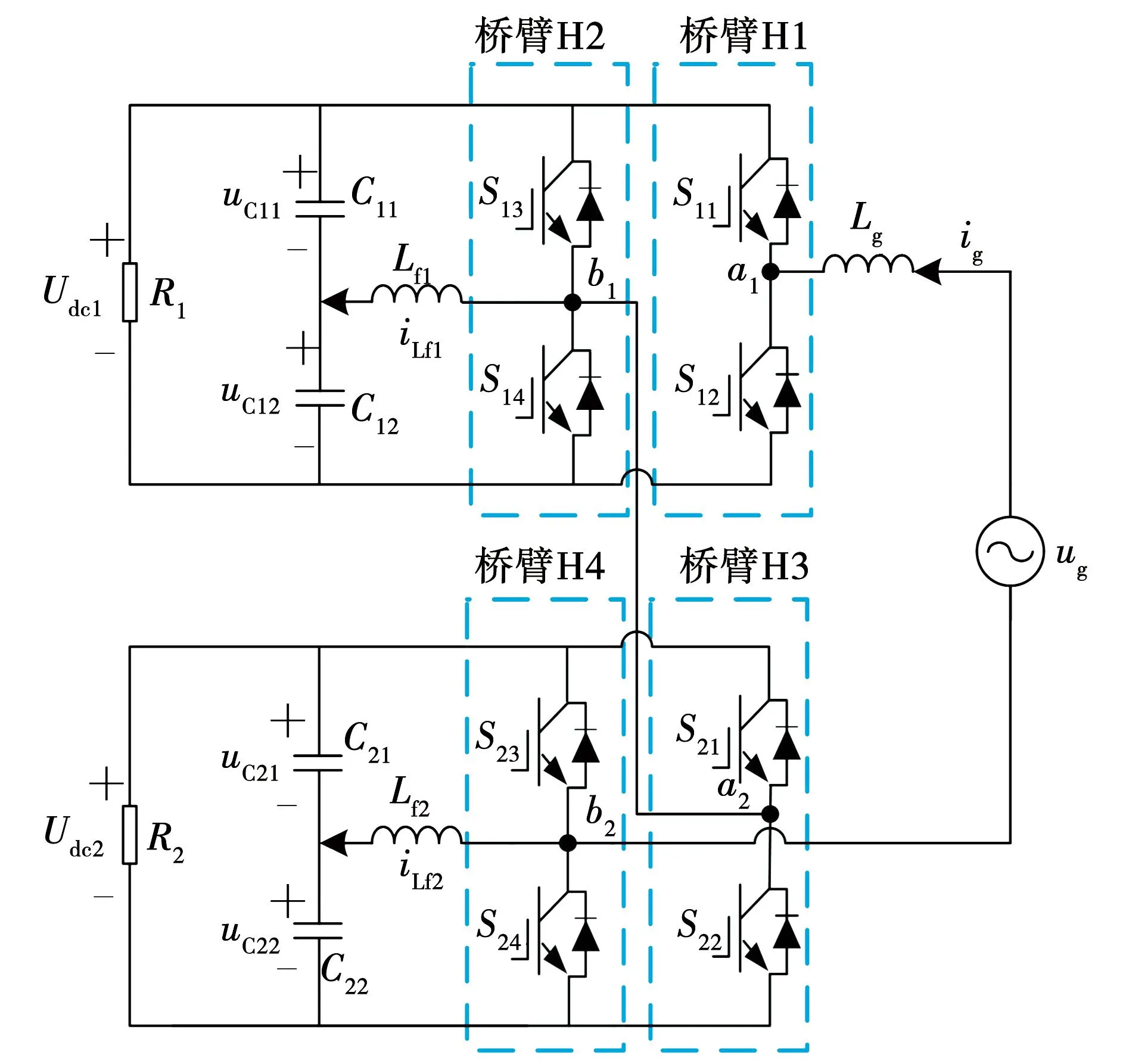
图1 单相CHBR复用式APD拓扑结构图Fig.1 Single-phase CHBR multiplexing APD topology diagram
该拓扑的基本原理即将系统固有的二次纹波功率存储在由体积容量更小、寿命更长的MAPD电路中,从而有效减少直流侧输出电压的二次电压脉动,提高系统的可靠性。此拓扑具有桥臂复用的情况,即桥臂H2、H4既参加整流也参加解耦,由于大多数有源功率解耦拓扑需附加额外的有源器件,如文献[13]中所介绍的多种APD拓扑需要额外的2~4个开关管,将会导致更高的实施成本,尤其是随着级联模块数量的增加,这一特性将更加明显,图1拓扑较多数有源功率解耦电路相比,无需增添有源器件,降低了实施成本。
为了进一步分析图1拓扑的原理,设电网电压的角频率为ω,幅值为Ug,交流侧输入电流幅值为Ig,则交流侧电压和电流可表示为:
(1)
其中φ为交流侧输入电压与输入电流的夹角。
忽略网侧电感消耗的功率,根据电压电流表达式,则交流侧瞬时功率pg表达式为
(2)
从式(2)可知交流侧瞬时功率包含二次纹波功率,其传递到直流侧会使直流侧输出电压衍生二次纹波电压,为使二次纹波功率从直流母线上转移,需对解耦单元进行调制。
在电容匹配(Ci1=Ci2=C)的情况下,为达到最佳的解耦效果,文献[16]对单模块复用式解耦单元进行分析,令电容Ci1和Ci2的平均电压为Udci/2(i=1,2),再叠加上相位相差180°的基频电压分量,则uCi1和uCi2可表示为:
(3)
式中:uC为解耦电容交流电压;UC为解耦电容电压交流分量幅值;θ是电网电压与分裂电容电压交流分量之间的相位差。
通过对式(3)进行微分,并由KCL可得到流过分裂电容的电流iCi1和iCi2及解耦电感电流iLfi为:
(4)
则分裂电容提供的功率可表示为
(5)
当分裂电容匹配(Ci1=Ci2=C)时,式(5)可化简为
(6)
使式(6)与式(2)的时变项相等,得到:
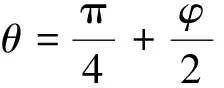
(7)
(8)
此时纹波功率可被分裂电容存储,为选取合适的θ值,对H2及H4桥臂开关管的电流应力进行分析,流过H2及H4桥臂的电流有效值IH2,4可表示为:
(9)
假定系统为单位功率因数运行,即φ=0,则由式(7)及式(9)可知当θ=π/4可使H2及H4桥臂开关管的电流应力有效值最低。
1.2 电容匹配下MAPD控制策略
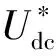
(10)
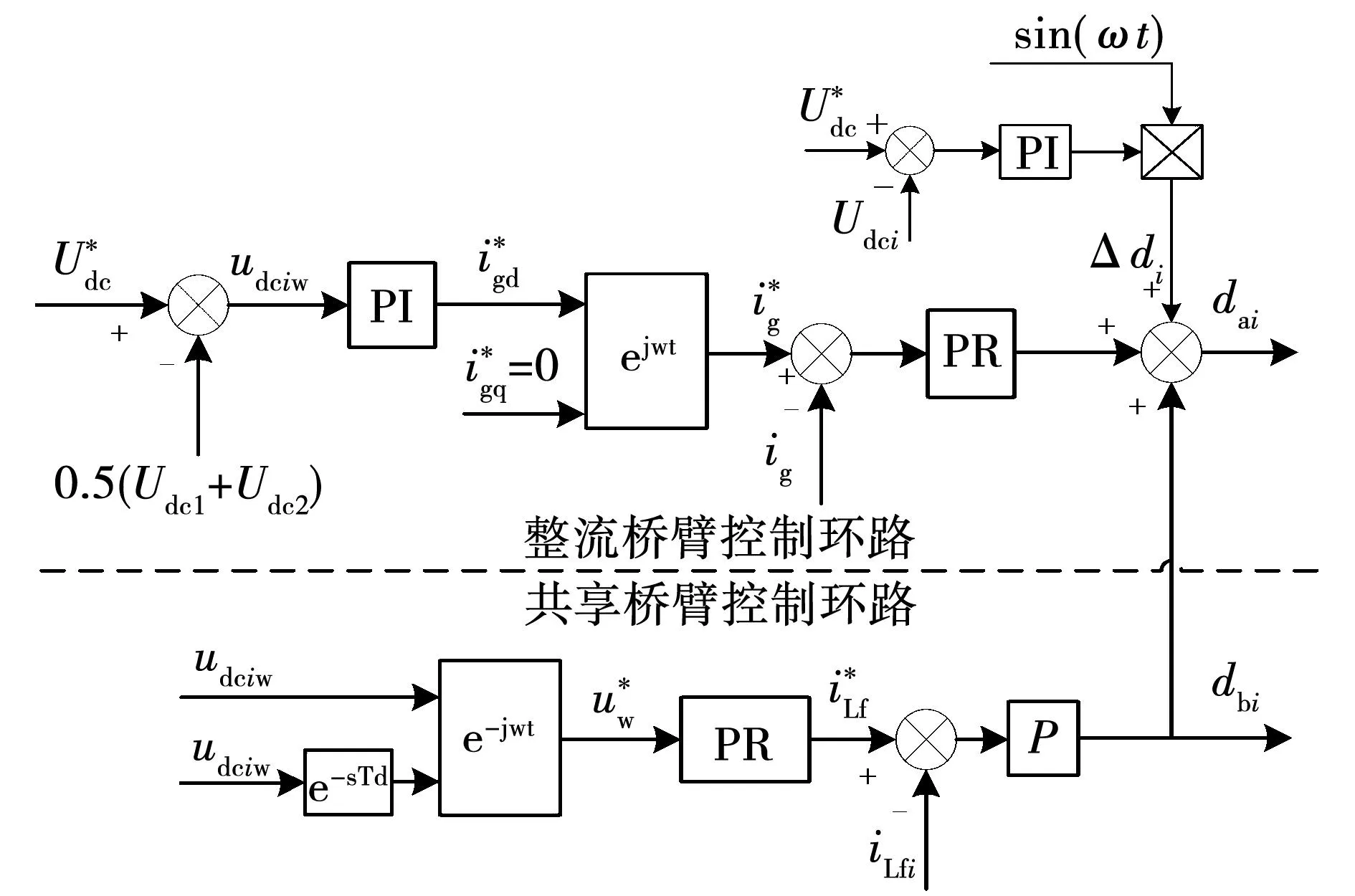
图2 电容匹配时控制策略框图Fig.2 Control strategy block diagram for capacitor matching
正交变换后的二倍频纹波分量将会降成基频分量,外环经过谐振频率为ω的比例谐振控制器PR后输出解耦电感电流的参考值,内环使用比例控制器kp生成H2、H4桥臂的调制信号dbi。
对于此拓扑结构,每个环路的调制波信号只对一个桥臂进行控制,故使用单极性调制作为调制方式。对于整流桥臂H1、H3使用载波移相调制策略,H1桥臂的三角载波相比于H3桥臂的三角载波超前90°,对于共享桥臂H2、H4使用相同的三角载波。
2 电容失配下纹波分析
第1节讨论了电容匹配时的解耦工作原理,在实际情况中,电容容值会随温度等因素产生偏差,即便是薄膜电容也是如此,为了分析电容失配时仍采用图2控制策略是否会对系统解耦效果产生影响,假设分裂电容失配(Ci1≠Ci2)时容值分别为:
(11)
其中k为分裂电容的失配系数。为便于分析,暂且使两个解耦单元的失配系数相等,考虑到实际运行时每个级联模块中电容的失配程度可能不一致,在3.1节给出级联模块间失配系数不相等的情况分析。
电容失配时,系统稳定后两个级联模块直流侧输出电压相等,都为Udc,仍采用图2控制策略使分裂电容波形表示为式(3)的形式,则由式(5)及式(11)可得电容失配下分裂电容提供的功率为:
[(k-1)ωUdcUCC×cos(ωt+θ)+
(12)
由式(12)可知电容失配(k≠1)时分裂电容提供的功率除了有用于补偿固有二次纹波功率之外,还产生了一次功率分量,为验证此一次功率分量对功率解耦产生的影响,令两个级联单元的失配系数k=1.2,并使用图2控制策略进行仿真验证,参数设置如表1所示。

表1 MAPD型单相CHBR系统参数Table 1 Parameters of MAPD single-phase CHBR system
图3和图4分别为电容匹配与失配时使用图2控制策略得到的直流侧电压及分裂电容电压仿真波形,其中Udc1和Udc2代表直流母线电压,uC11、uC12、uC21、uC22代表分裂电容电压。由图3和图4对比可知,当电容失配时直流侧电压的二次纹波分量同样得到了有效抑制,但衍生出了一次纹波分量,直流侧输出电压范围由图3的99.6~100.3 V变化成图4的96.5~103.4 V,且两个电容的电压幅值不再相等,这是由于分裂电容额外产生了一次功率分量,故仿真结果与式(12)分析一致。可见在图2控制策略下电容失配问题会降低MAPD电路的解耦精度。
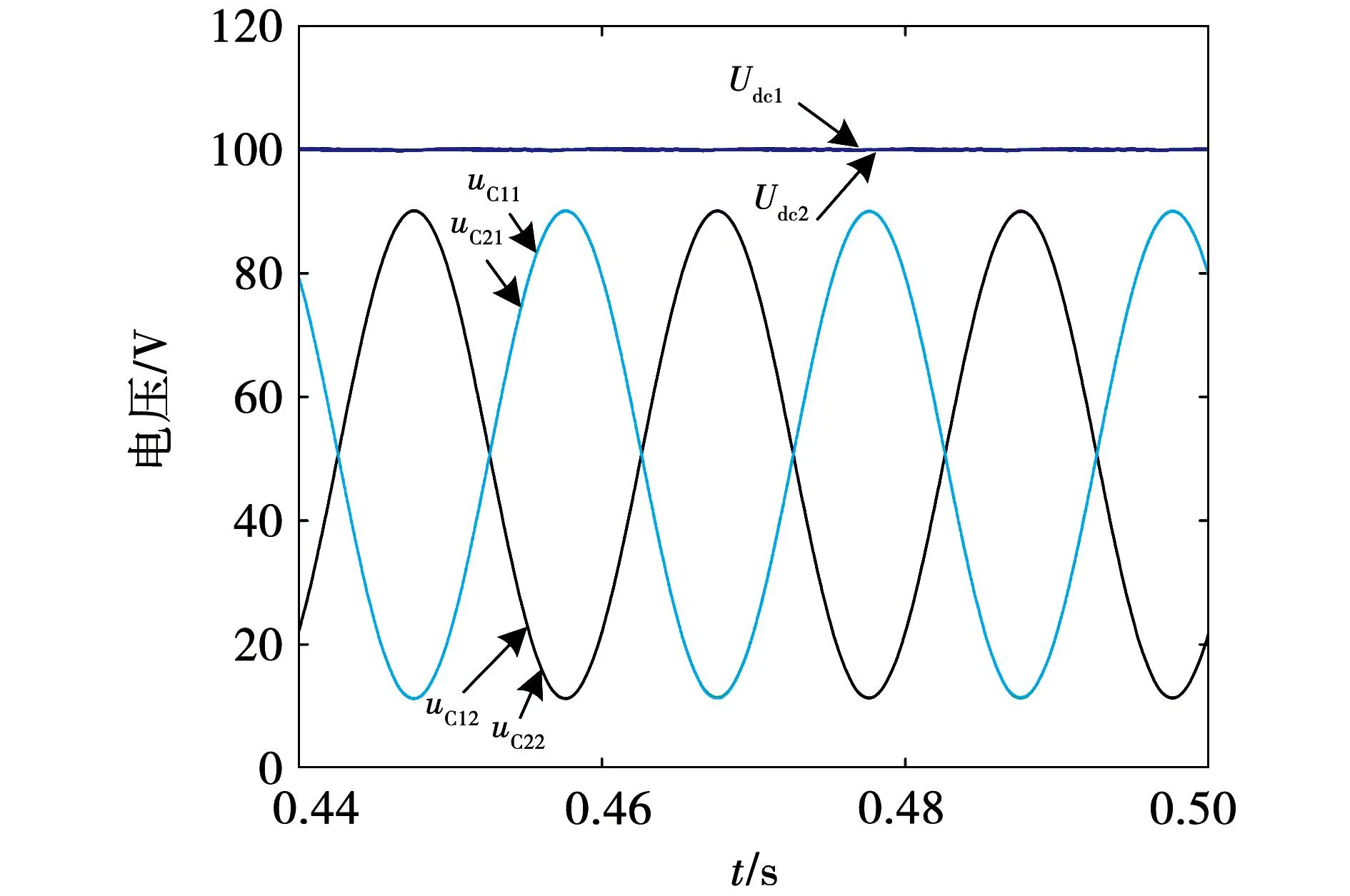
图3 电容匹配时直流侧电压及分裂电容电压波形Fig.3 DC side voltage and split capacitor voltage waveforms when capacitors are matched
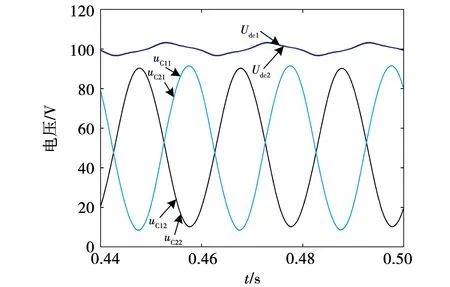
图4 电容失配时直流侧电压及分裂电容电压波形Fig.4 DC side voltage and split capacitor voltage waveforms when capacitors are not matched
结合图5,此一次纹波分量传递到交流侧会使交流侧输入电流衍生多余的直流偏置以及二次纹波分量,影响解耦效果和网侧电能质量。为便于分析,假设网侧电流衍生出零相位的二次纹波分量,则网侧电流可表示为
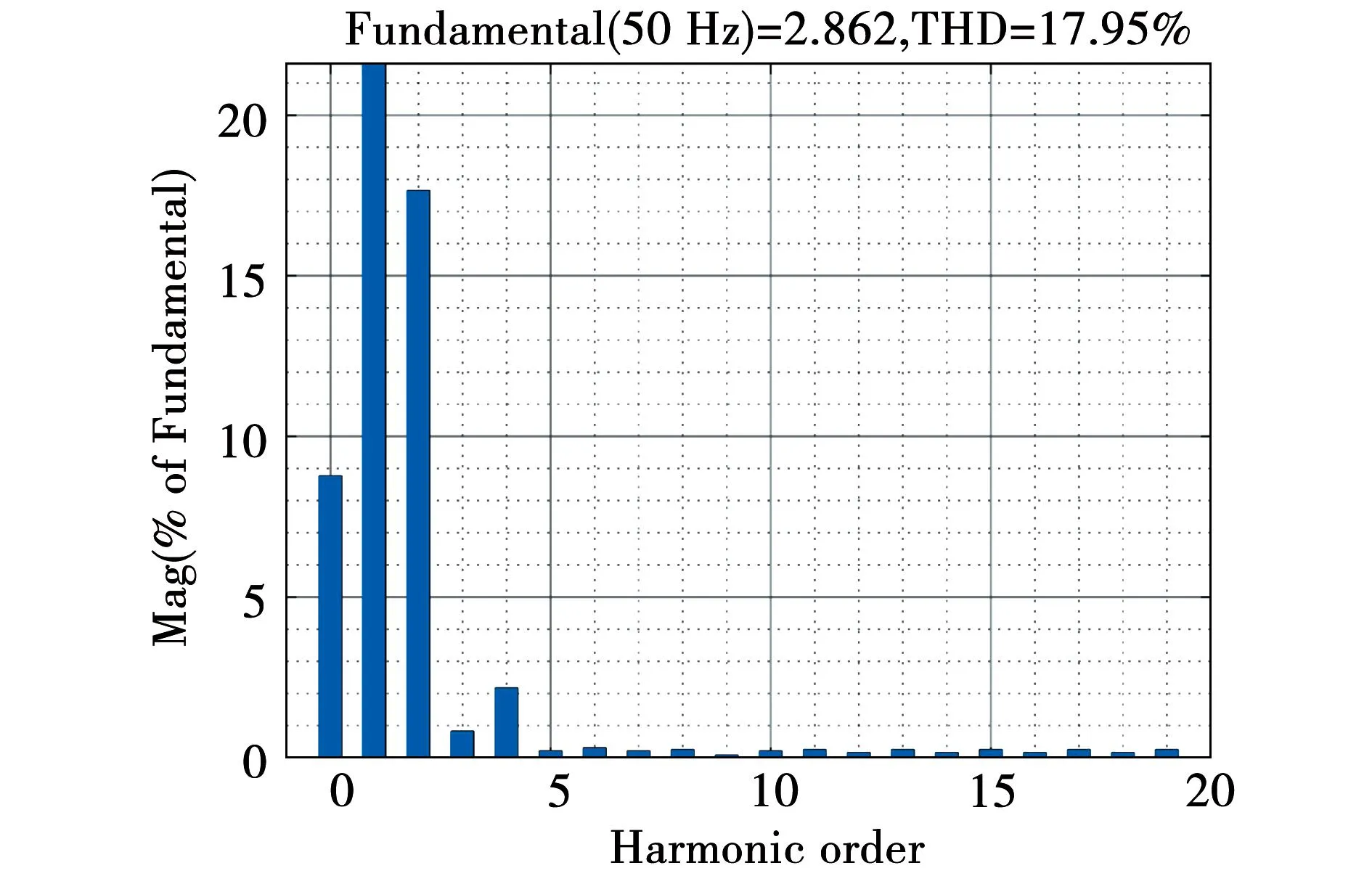
图5 电容失配时网侧电流频谱图Fig.5 Grid-side current spectrum diagram when capacitors are mismatched
ig=Idc+Igsin(ωt+φ)+I2ωsin(2ωt)。
(13)
其中:Idc代表网侧衍生出的直流分量幅值;I2ω代表衍生出的二次纹波分量幅值。
此时网侧瞬时功率表达式变为:
pg=ugig=Ugsin(ωt)[Idc+Igsin(ωt+φ)+
(14)
其中M1和δ分别为一次纹波功率分量的幅值和相位,其表达式为:
(15)
(16)
将式(14)与式(12)的一次纹波功率分量相等,可以得到:
(17)
(18)
为探究失配系数k与衍生分量的关系,结合式(7)、式(8),画出衍生分量幅值Idc及I2ω在网侧电流基频分量幅值Ig的占比与失配系数k的关系图,如图6所示。
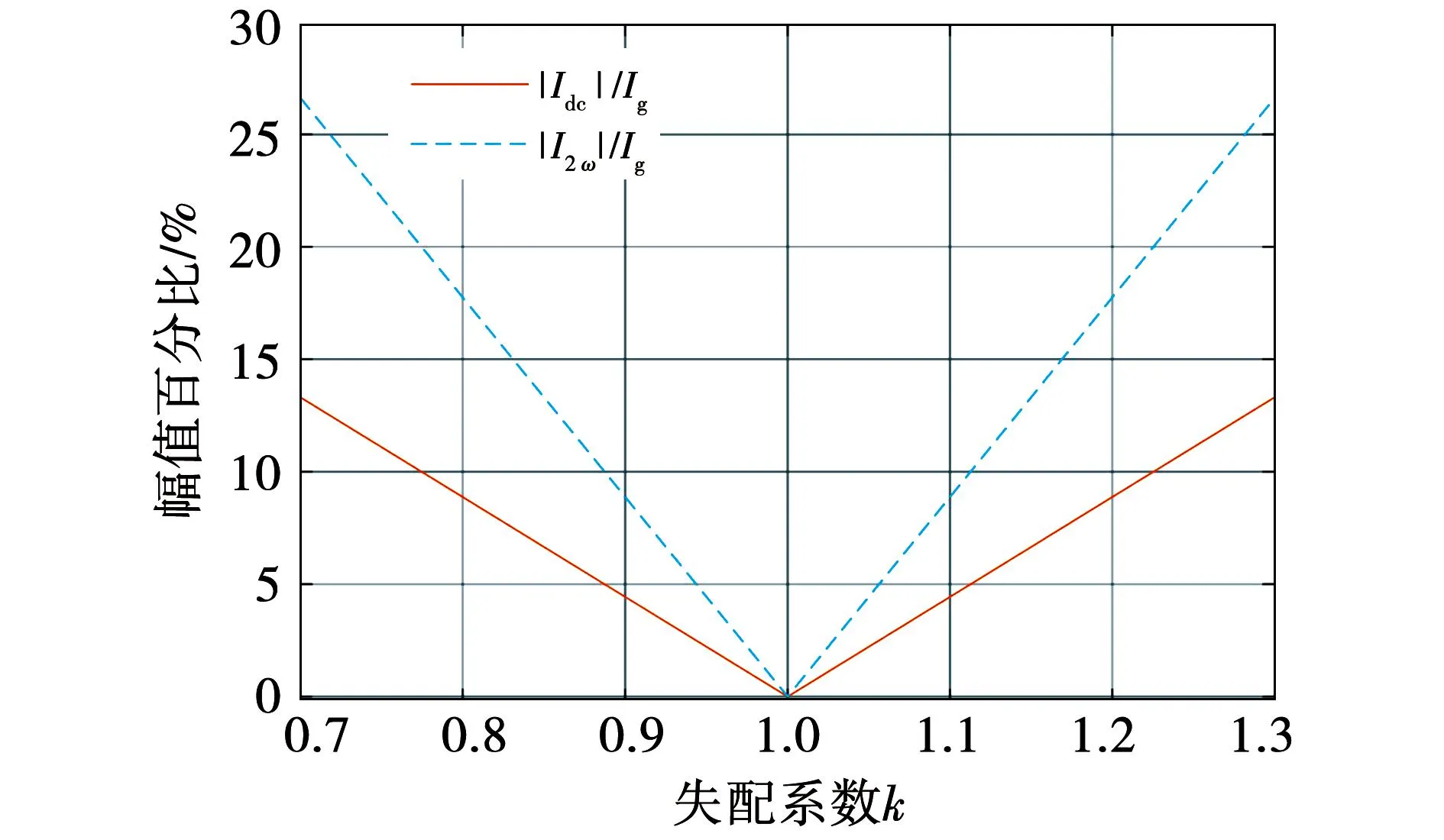
图6 衍生分量幅值占比与失配系数关系图Fig.6 Relationship between the amplitude ratio of the derivative components and the mismatch coefficient
由图6可知,当失配系数k不等于1时,网侧衍生出的直流偏置幅值占比及二次纹波分量幅值占比随着失配系数偏离1的程度增大而逐渐上升,图2的控制策略无法使系统达到正常的解耦效果,需应用一种新的解耦控制方法。
3 电容失配下控制策略
3.1 纹波抑制方法
本文对于单相CHBR分裂电容型复用式功率解耦电路在电容失配情况下采用修改分裂电容电压参考值的方法,将式(3)修改成不同直流偏置叠加相位相差180°的二倍频电压分量,表示为:
(19)
其中Udci1和Udci2分别为电容电压的直流偏置。
通过对式(19)进行微分,并由KCL可得到流过分裂电容的电流iCi1和iCi2及解耦电感电流iLfi为:
(20)
则分裂电容提供的功率可以表示为:
(21)
式(21)与式(12)不同的是分裂电容提供的功率不再含有一次功率分量,而是产生了一个幅值较小的四次功率分量,其相对二次功率分量幅值较小,可以忽略。令式(2)与式(21)中的二次纹波功率相等,可以得到:
(22)
式(19)中的直流偏置Udci1和Udci2可进一步表示为:
(23)
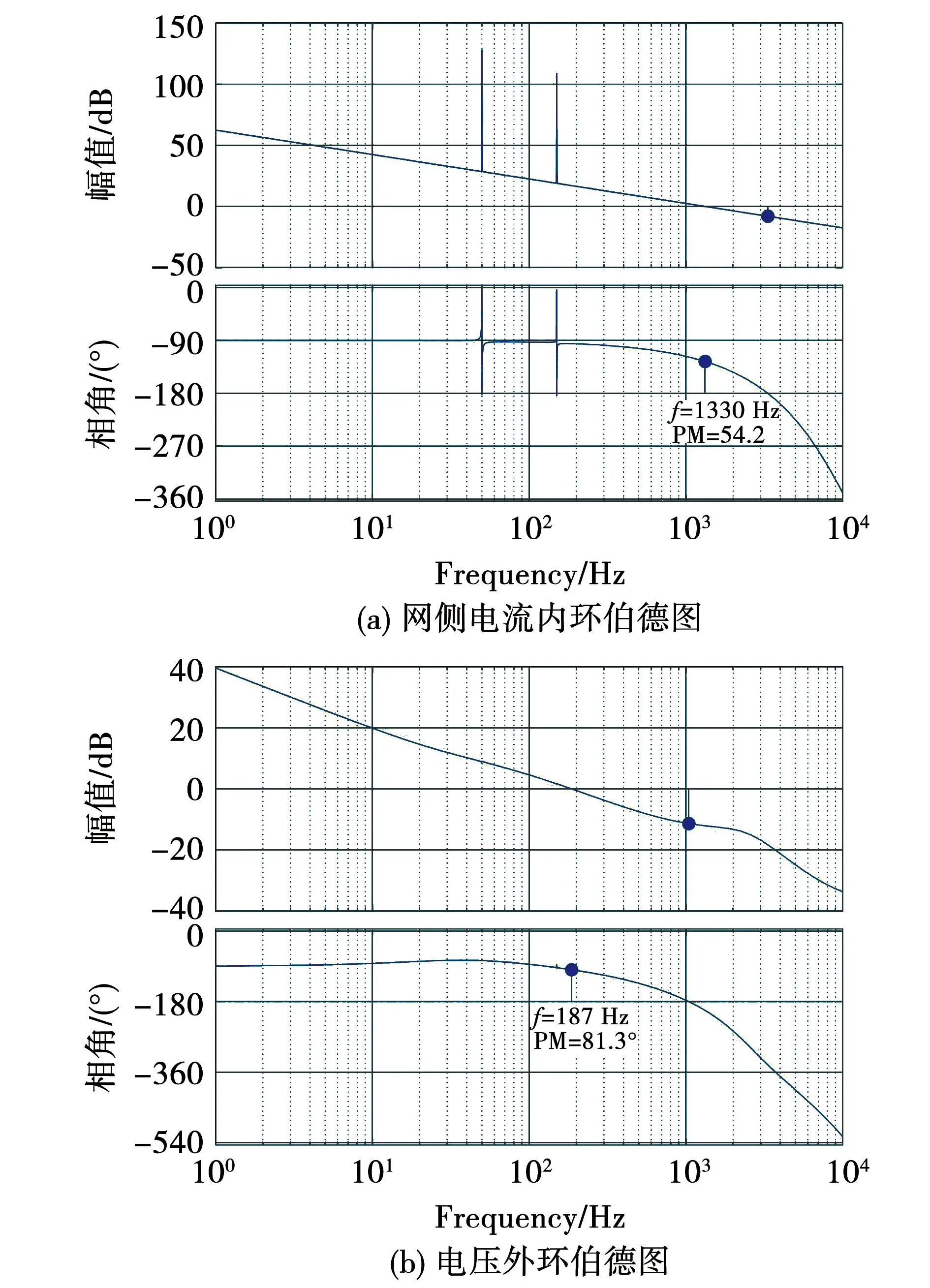
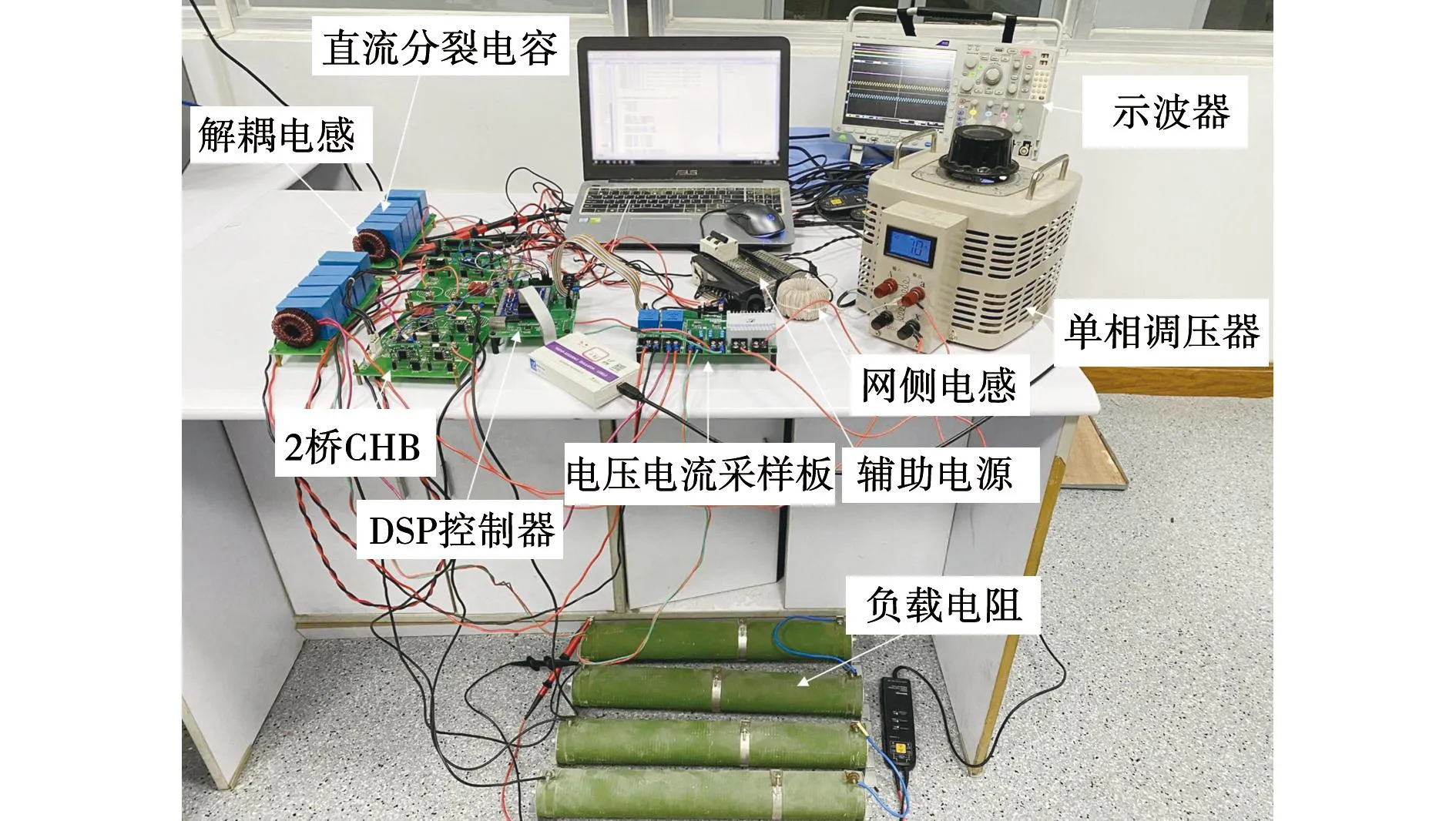
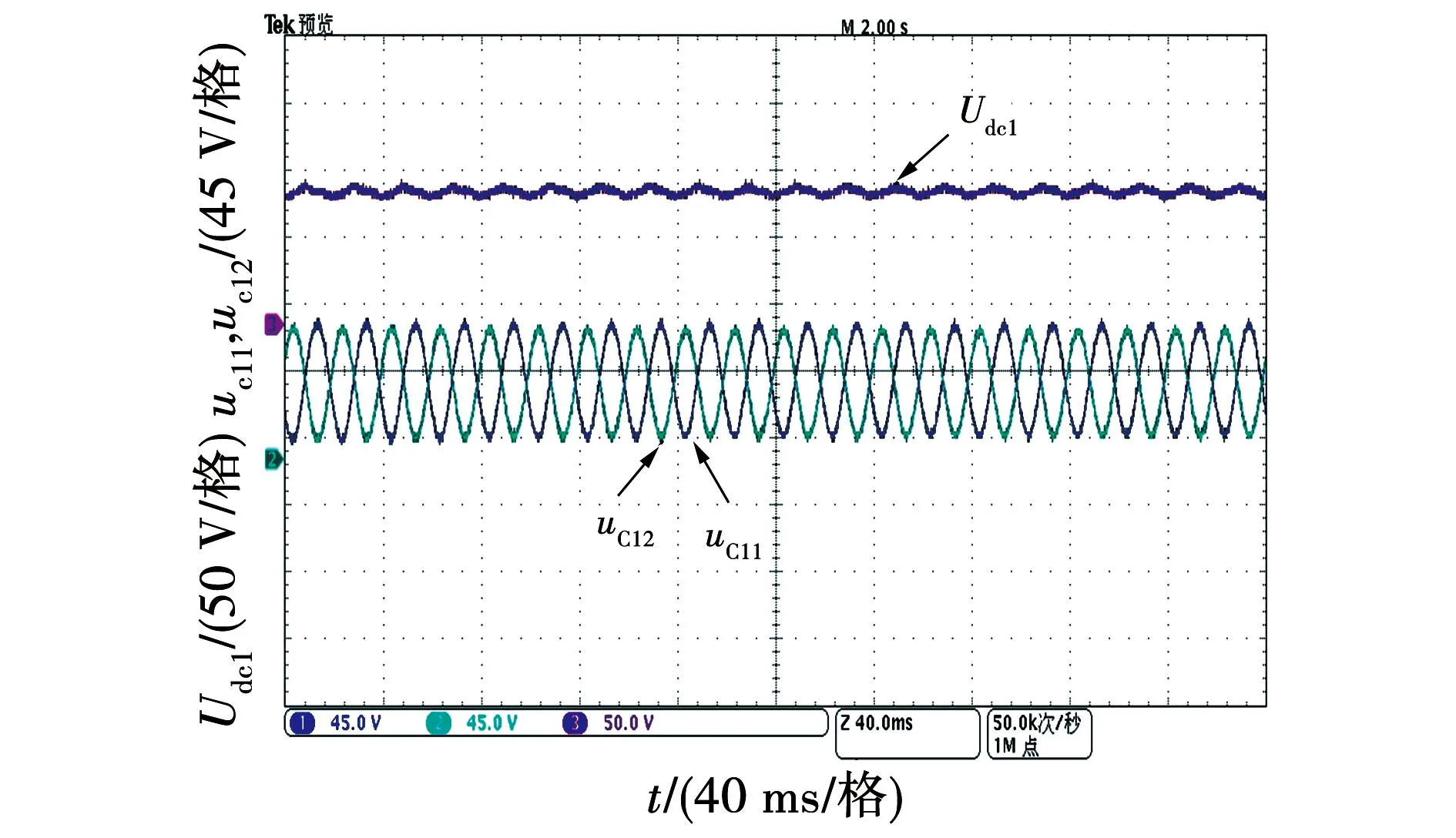
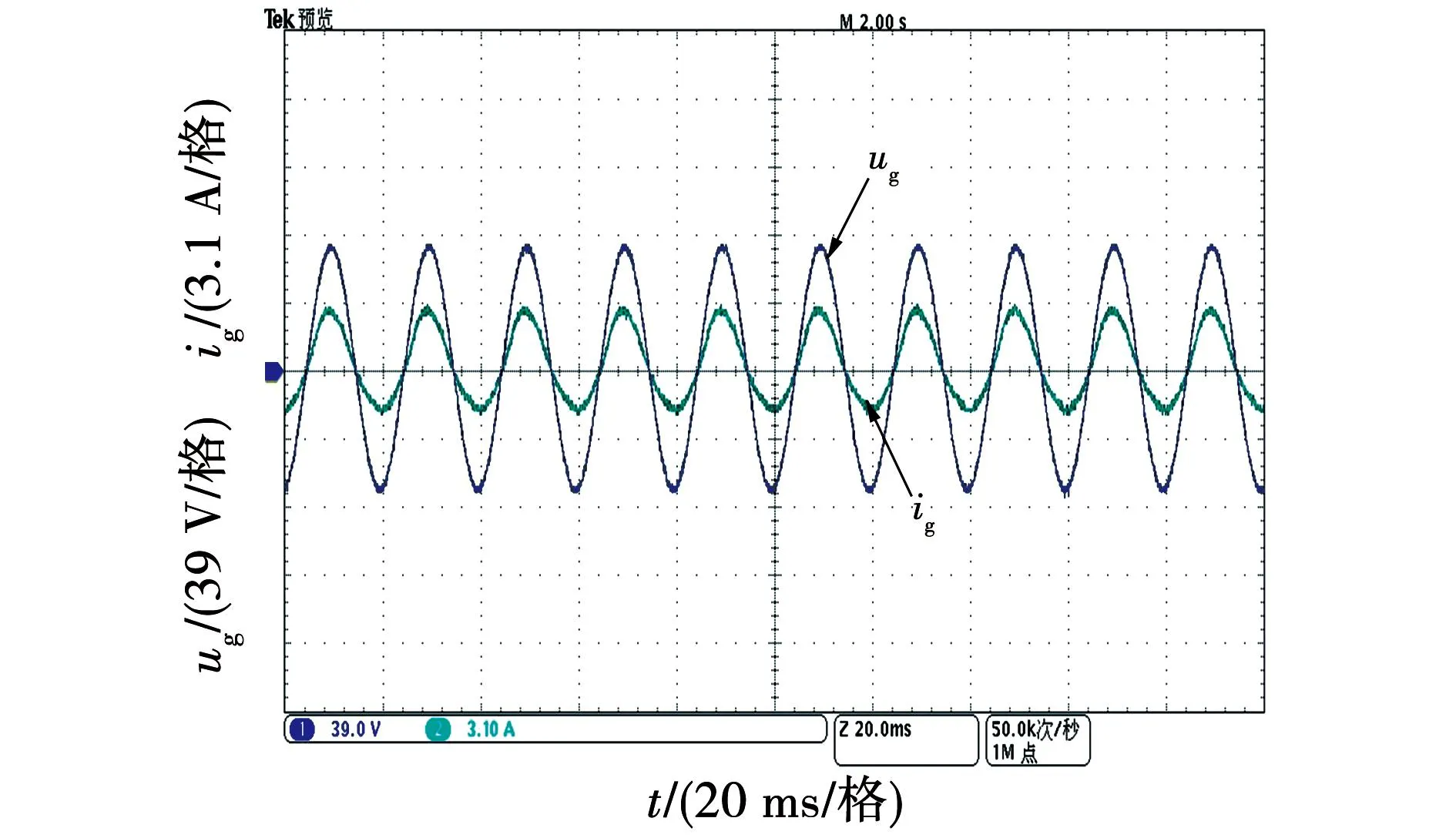
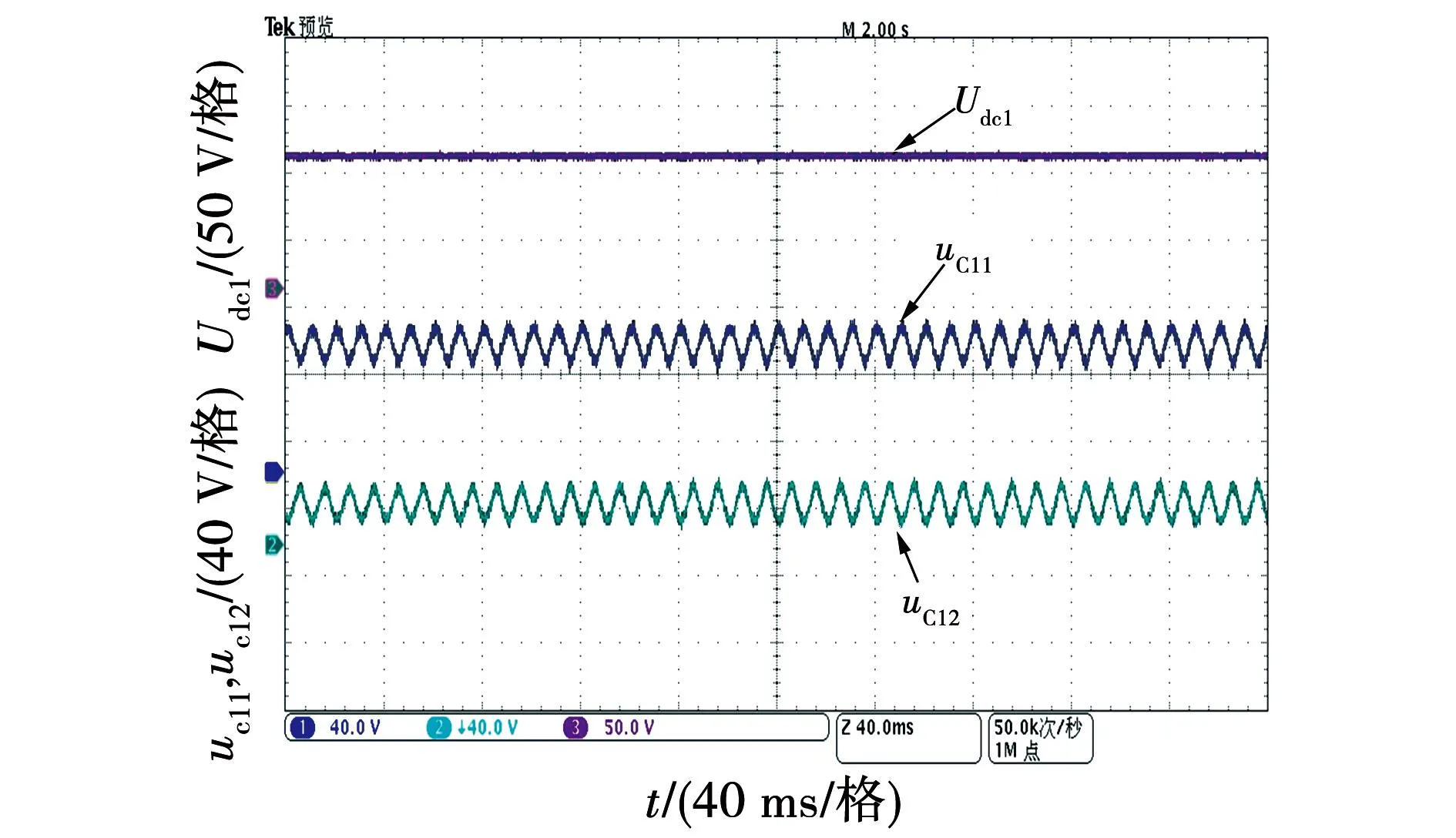
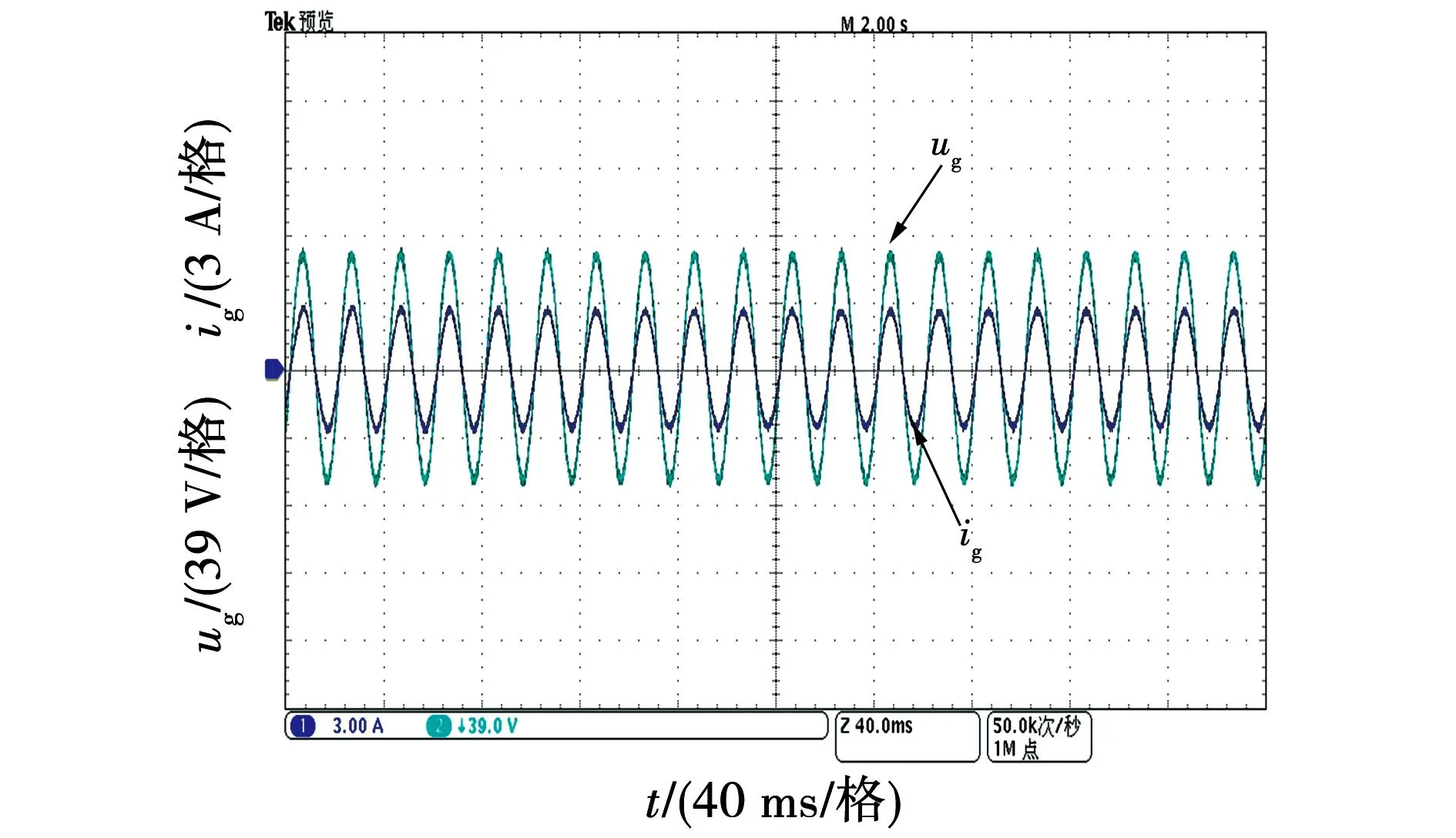
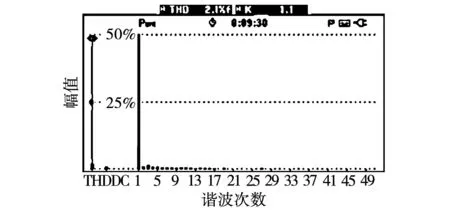
式中m为直流偏置系数(0 (24) (25) 由式(25)可得到电容电压交流分量幅值UC与m的关系,如图7所示。 图7 电容电压交流分量幅值与直流偏置系数关系图Fig.7 Relationship between amplitude of AC component of the capacitor voltage and the DC bias coefficient 由图7可知,在m=0.5时电容电压交流分量幅值为无穷大,这种情况显然需要排除掉,可见应该合理选择m值,以免影响解耦效果。 当考虑失配系数k≠1时,式(21)变为 (26) 将式(26)与式(2)的二次纹波功率相等,并结合式(23),可以得到: (27) 由式(24)及式(26)可知,无论失配系数k是否为1,采用本文所提式(19)的形式都不会衍生出额外的纹波功率分量,即所提控制策略可适用于电容匹配与失配两种情况,可见本文所提方法具有鲁棒性。 由于直流偏置系数m的取值会影响该方法的解耦性能,应从分裂电容电压的角度进行分析。由1.1节可知,电容的电压取值范围在0与Udci之间,则有: (28) 将式(23)代入式(28)可得: mUdci-UC>0。 (29) 将式(27)代入式(29)并假设两级联模块直流侧输出电压相等,化简可以得到m的极值为 (30) 结合实际电容容值参数漂移情况,选取失配系数k的取值范围为0.76到1.27,由式(30)画出m的极值与失配系数k的关系如图8所示。 图8 直流偏置系数取值范围与失配系数关系图Fig.8 Relationship between value range of DC bias coefficient and the mismatch coefficient 由图8可知,随着失配系数k的增加,直流偏置系数m的取值范围逐渐增加,为满足失配系数从1向两端变化的情况,m值选择取值范围最小时的中间值,由图8计算出m值为0.25,此时当失配系数k在此范围内变化时电容电压始终满足式(28)。因此,当级联模块间失配系数k不相等但都在此范围内变化时,m取0.25均可满足要求。 当电容失配时,以表1参数为例,即使每个级联模块上Ci1增加了20 μF,但相对于传统无源滤波所需电容容值小得多,由式(31)可计算无源滤波所需的电容容值大小为: (31) 其中ΔUdc代表直流侧输出电压允许的电压纹波范围。若取ΔUdc为0.2 V,由式(31)并结合表1参数,则每个级联模块使用无源滤波时所需电容值为3 978 μF,因此采用本文拓扑时每个级联模块所需的容值仅为传统无源滤波方式所需电容容值的1/39,有效减少了整体的体积。 对电容失配下的主电路进行数学建模,为便于分析,不计开关器件的损耗以及电容元件的寄生电阻。对图1所示的主电路应用KCL则有: (32) 其中:dai(i=1,2)代表H1及H3桥臂的调制信号;dbi代表H2及H4桥臂的调制信号;Ceq为每个解耦电路中的串联等效容值。 因为直流侧电压及电流中均含有纹波分量,为体现这一特性,可将式(32)改写为 (33) 其中下标0和w分别代表恒定直流量和纹波分量。 式(33)中的纹波分量仅由解耦桥臂控制,整流桥臂控制回路不参与此过程,故式(33)可以简化为: (34) 对图1主电路由KVL及KCL可得: (35) (36) (37) (38) 将式(36)与式(35)相减得到 (39) 对式(37)由线性化及拉普拉斯变换可得 (40) 对式(38)、式(39)进行小信号建模及线性化可得 (41) (42) 由式(40)并对式(41)、式(42)进行拉普拉斯变换可得整流桥臂控制环路的网侧电流内环及共享桥臂控制环路的解耦电感电流内环的传递函数分别为: (43) (44) 对式(34)使用小信号建模及线性化可得 (45) 将式(35)与式(36)相加得到: (46) 由于纹波分量仅由共享桥臂进行控制,故结合式(34)与式(46)可得: (47) 对式(47)使用小信号建模及线性化可得: (48) 对式(45)、式(48)进行拉普拉斯变换并结合式(43)与式(44)可得整流桥臂控制环路及共享桥臂控制环路的直流侧电压外环的传递函数分别为 (49) (50) 由第2节分析可知,当分裂电容发生参数漂移时(k≠1)时,图2原有控制策略不能得到正常的解耦效果,直流侧电压会衍生出一次纹波分量,传递到网侧则会影响到网侧电流质量。由3.1及3.2节纹波抑制方法及数学建模,本文提出一种适用于电容失配时的双电压环控制策略,如图9所示。 图9 电容失配情况下控制策略框图Fig.9 Control strategy block diagram in case of capacitor mismatch 整流桥臂控制环路的设计可以遵循传统PWM整流器的标准控制器设计。由于纹波分量由共享桥臂控制环路处理,故整流桥臂控制环路的电压外环无需再使用低通滤波器,带宽也会变大,故电压外环使用PI控制器即可,其传递函数为 (51) 由式(21)可知直流侧纹波功率中含有二次及四次纹波功率,传递到交流侧会衍生三次纹波分量,故整流桥臂控制环路电流内环应采用多比例谐振控制器,谐振频率应为ω和3ω,传递函数为 (52) 经过多比例谐振控制器后的调制信号叠加共享桥臂控制回路的调制信号dbi以及电压均衡模块的补偿调制信号Δdi生成整流桥臂的调制信号dai。 对于电压电流双闭环控制器增益的选取,应保证电流内环的带宽足够大以确保能获得较快的动态响应速度,而电压外环的带宽应远小于电流内环的带宽,通常选取电流内环的带宽为开关频率的1/10~1/5,电压外环的带宽设计为电流内环带宽的1/10~1/7。 在共享桥臂控制环路中,由于其作用是将udciw抑制为零,故将udciw与零做比较作为输入。由于二次纹波分量为交流量,故共享桥臂控制环路的电压外环选用PR控制器。同样由式(21)可知直流侧纹波功率中含有二次及四次纹波功率,故共享桥臂控制环路中应使用多比例谐振控制器,其谐振频率应为2ω和4ω,其传递函数为 (53) 在解耦电流控制回路中,由于解耦电感电流的波形并非一定要求为正弦形状,故电流内环选择简单的比例控制器Kp即可,传递函数为 G4=kp4。 (54) 在比例控制器输出后叠加直流偏置系数以及0.5系数,最后得到共享桥臂控制回路的调制信号dbi(i=1,2)。共享桥臂控制环路中的控制器参数的选取仍按照电压电流双闭环控制器增益选取规则,此处不再赘述。 为验证系统稳定性,根据表1及3.2节所得传递函数并考虑计算延迟分别绘制整流桥臂控制环路和共享桥臂控制环路的电流内环及电压外环的开环伯德图,分别如图10和图11所示。 图10 整流桥臂控制环路开环伯德图Fig.10 Open loop Bode diagram of rectifier bridge arm control loop 图11 共享桥臂控制环路开环伯德图Fig.11 Open loop Bode diagram of shared arm control loop 由图10可知,网侧电流在50 Hz和150 Hz处发生谐振,电流内环的穿越频率为1 330 Hz,其相位裕度在穿越点之前位于-180°~0°范围内,在穿越频率处其PM数值为54.2,电压外环的穿越频率为187 Hz,PM数值为81.3,可见电流内环能快速反应,外环带宽比传统电压外环带宽大,系统稳定。 由图11可知,解耦电感电流内环在282 Hz处发生谐振,电流内环的穿越频率为1 260 Hz,PM数值为56.1,电压外环含有两处谐振,穿越频率为117 Hz,PM数值为45.3,系统稳定。 在仿真软件中搭建MAPD型单相CHBR模型,仿真参数如表1所示。 首先验证电容失配时图9控制策略的有效性,取级联两个单元的失配系数k1=k2=1.2,即C11=1.2C12=120 μF,C21=1.2C22=120 μF,令R1=R2=200 Ω,图12为电容失配情况下网侧电压电流波形,可知系统可以实现电压电流同相位,实现单位功率因数整流。图13为输入侧电压Ua1b2波形,呈现为五电平阶梯波。图14为使用本文所提控制策略下的网侧电流频谱图,结合图5和图14可知,本文所提控制策略可有效抑制网侧电流衍生出的直流偏置及二次纹波分量,使系统THD值减小。 图12 网侧电压电流波形Fig.12 Grid side voltage and current waveform 图13 输入侧电压波形Fig.13 Input side voltage waveform 图14 网侧电流频谱图Fig.14 Grid side current spectrum diagram 图15所示为电容失配情况下(k1=k2=1.2)得到的波形,由于容值偏差的原因,分裂电容的电压变为不同的直流偏置叠加幅值相同、相位相差180°的二次谐波分量,直流侧电压的波动范围为100±0.2 V,结合图4中直流侧电压波动范围可知本文所提控制策略可有效抑制直流侧电压衍生出的一次纹波分量,提高了解耦精度。 为验证级联模块间失配系数不相等时本文所提控制策略的有效性,令第一个和第二个H桥单元的失配系数分别为k1=1.2、k2=1.3,得到的直流侧电压及电容电压波形如图16所示,直流侧电压的波动范围为100±0.2 V,由于失配系数不相等,两个级联模块电容电压的交流分量幅值不相等,验证了式(27)的正确性。可知当级联单元间失配系数不相等时,所提控制策略仍可以实现较好的解耦效果。 图16 级联模块间失配系数不相等时仿真波形Fig.16 Simulation waveforms when mismatch coefficients between cascaded modules are not equal 为验证本文所提控制策略的动态性能,在k1=k2=1.2的情况下,仿真设置负载由R1=R2=200 Ω在某一时刻突变为R1=150 Ω,R2=145 Ω,由图4、图15和图17可知,本文所提控制策略不仅可以在电容失配情况下对直流侧电压衍生的一次纹波分量进行有效抑制,且可以在负载突变后较短时间内再次达到稳定状态,具有抗扰特性好的特点。 图17 直流侧电压及分裂电容电压波形Fig.17 DC side voltage and split capacitor voltage waveform 搭建了MAPD型单相CHBR小功率实验平台,实验平台结构框图及实物图分别如图18和图19所示,其中主控制器采用DSP28335控制板,开关管采用MOSFET,型号为IRFP460,网侧电感及解耦电感均使用购买的高磁通磁粉芯绕制,网侧电感使用利兹线,解耦电感使用漆包线。电容匹配时使用两个50 μF的EPCOS薄膜电容并联形成Ci1和Ci2,实验主电路参数如表1所示。 图18 MAPD型单相CHBR实验平台结构框图Fig.18 Structure block diagram of MAPD single-phase CHBR experimental platform 图19 MAPD型单相CHBR实验平台实物图Fig.19 Physical map of MAPD single-phase CHBR experimental platform 首先验证电容失配在图2控制策略下的波形,分别在C11和C21两端并联20 μF的EPCOS薄膜电容模拟电容失配状态,稳态时得到的直流侧电压Udc1、两个电容电压uC11和uC12以及网侧电压电流的实验波形如图20和图21所示,使用FLUKE435设备对网侧电流进行测量,得到的谐波分析如图22所示。由图20可以看出,由于电容失配的影响,尽管直流侧输出电压中二次纹波分量被抑制,但衍生出了一次纹波分量,直流侧输出电压的波动范围在95~105 V之间,且两个电容电压幅值不再相等,与第二节分析及仿真结果一致。由图21和图22可见电容失配时网侧电流衍生出了幅值较高的直流偏置量以及2次谐波分量,总谐波含量不符合国家标准《电能质量公用电网谐波》(GB/T 14549—1993)中规定的网侧电流总谐波含量低于5%的要求。 图20 电容失配时采用图2控制策略的实验波形Fig.20 Experimental waveforms with the control strategy in Figure 2 when the capacitors are mismatched 图21 电容失配时采用图2控制策略的实验波形Fig.21 Experimental waveforms with the control strategy in Figure 2 when the capacitors are mismatched 图22 采用图2控制策略下稳态时网侧电流THDFig.22 Grid-side current THD in steady state under the control strategy shown in Figure 2 图23、图24和图25为使用本文所提控制策略在电容失配时的实验波形及网侧电流谐波分析。从图23可见直流侧输出电压的波动范围为100±1 V,结合图20中直流侧输出电压的波动范围可知,所提控制策略提高了MAPD电路的解耦精度。两个电容的电压uC11和uC12变成不同的直流偏置量叠加幅值相同、相位相差180°的二次谐波分量,与仿真部分一致。从图24可知网侧电压电流同相位,实现单位功率因数整流。结合图22与图25可见,由于电容失配衍生出幅值较高的直流偏置以及二次谐波含量得到有效抑制,且网侧电流总谐波含量符合国家标准《电能质量公用电网谐波》(GB/T 14549—1993)中规定的网侧电流总谐波含量低于5%的要求。 图23 电容失配时采用本文所提控制策略的实验波形Fig.23 Experimental waveforms of the proposed control strategy when the capacitors are mismatched 图24 网侧电压电流的实验波形Fig.24 Experimental waveforms of grid-side voltage and current 图25 本文所提控制策略下稳态时网侧电流THDFig.25 Grid-side current THD in steady state under the proposed control strategy 为验证本文所提控制策略的抗扰性能,在某一时刻负载由R1=R2=200 Ω在某一时刻突变为R1=155 Ω、R2=160 Ω,实验波形如图26所示,可见直流侧电压可以在较短时间内再次恢复到稳定状态,说明了本文所提控制策略具有不错的抗扰性能。 图26 直流侧电压Udc1和Udc2的实验波形Fig.26 Experimental waveforms of DC side voltages Udc1 and Udc2 本文介绍了一种单相CHBR结合MAPD电路的拓扑,针对目前MAPD式分裂电容型功率解耦电路由于电容失配而降低解耦性能并衍生多余纹波的问题,提出一种新的控制策略,主要结论如下: 1)在电容失配下对MAPD型电路衍生纹波进行分析,对MAPD型电路进行数学建模。 2)提出修改分裂电容的参考电压,设计了一种鲁棒性好的控制策略,可以适用于电容匹配以及级联模块间失配系数相等和不相等时的情况,提高了MAPD电路的解耦精度,直流侧输出电压的波动范围由95~105 V变为99~101 V。 最后通过仿真及实验验证了所提控制策略可以实现在电容失配下达到较好的解耦效果,具有鲁棒性好、解耦精度高的特性。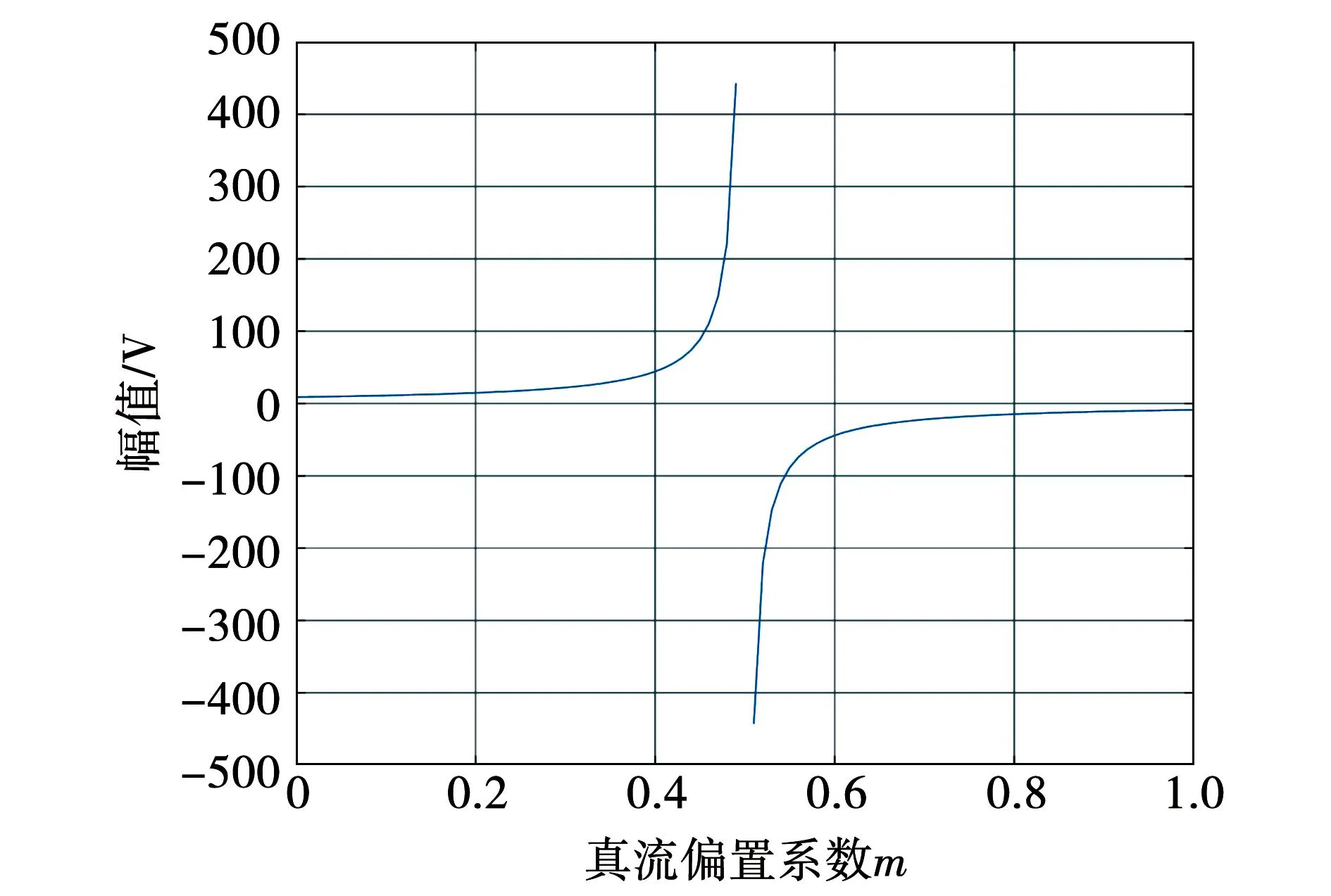
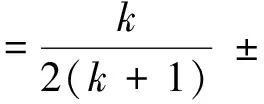
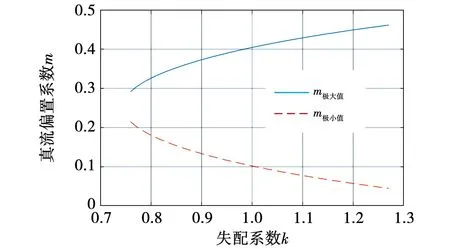
3.2 MAPD型单相CHBR数学建模
3.3 电容失配下控制策略及稳定性分析
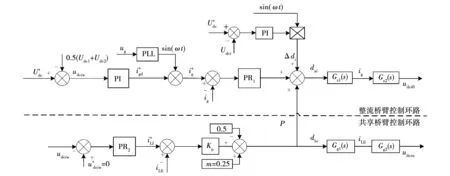
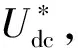

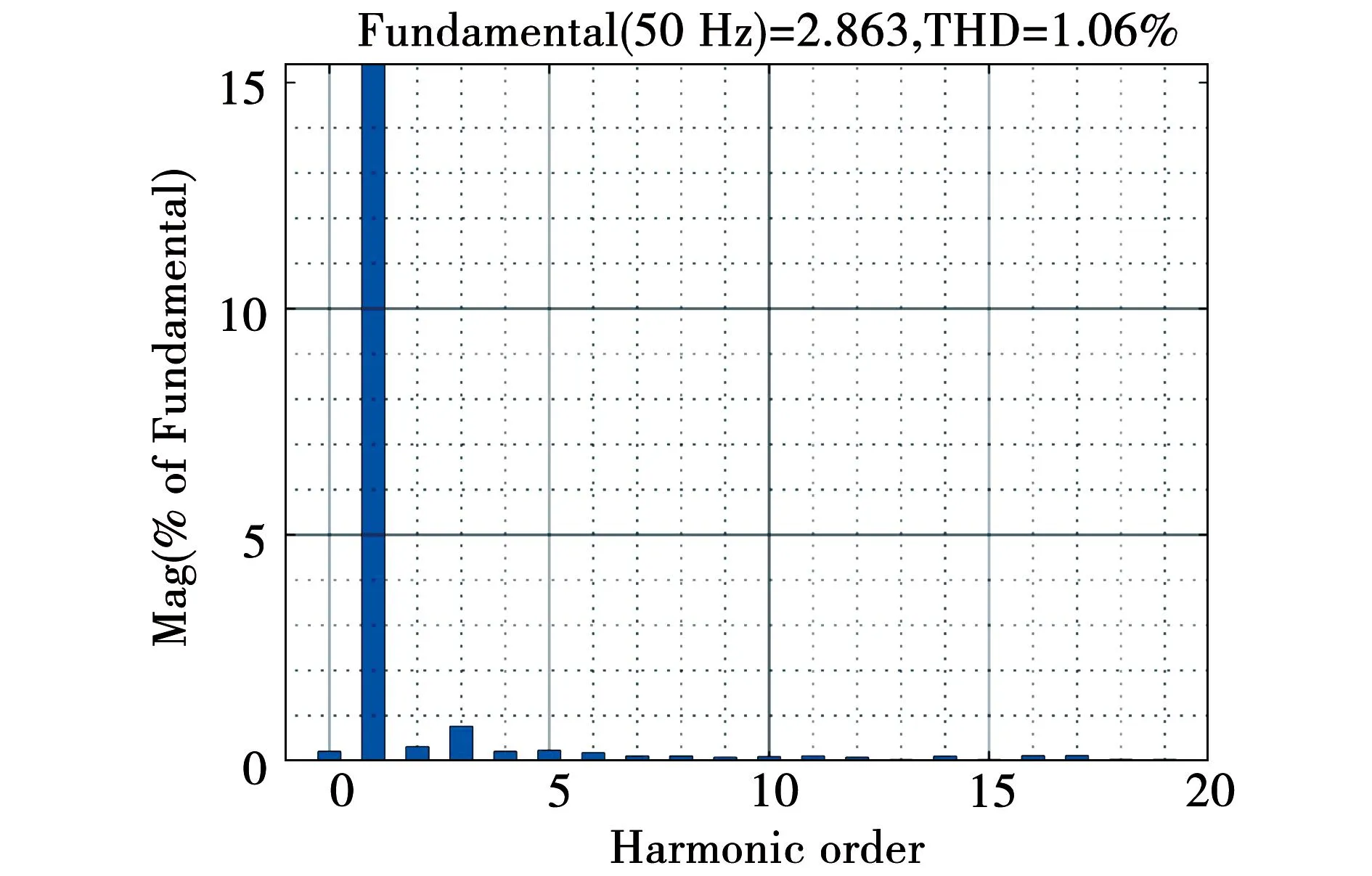
4 仿真和实验
4.1 仿真及分析


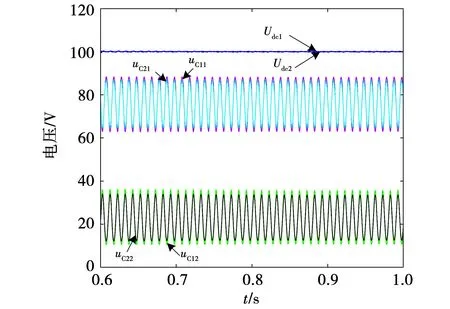

4.2 实验及分析



5 结 论
