混合风路高压感应电机电磁参量与损耗计算

戈宝军, 李同彬, 徐骁, 王越, 卜敬宇

(1.哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080; 2.佳木斯电机股份有限公司,黑龙江 佳木斯 154002)

0 引 言

感应电机性能可靠广泛应用于工业生产中,是重要负荷类型。随着单机容量不断增加,电磁负荷不断增大,高压成为感应电机行业发展趋势[1]。但其结构紧凑,导致散热效果差温升问题逐渐突显[2]。为了改善电机温升问题,提出混合通风冷却方式。但分析含混合通风结构的电机均忽略了混合通风结构对电机磁场和损耗的影响[3]。目前研究混合通风结构感应电机,采用轴向通风结构电机等效为混合通风结构电机的方法进行分析。但此方法将径向通风结构等效为无径向通风结构电机,无法全面考虑径向通风道边缘漏磁和转子通风槽板对电机磁场和性能参数的影响[4-5]。电机结构的变化会极大地影响电机磁场分布和性能参数,因此研究混合通风结构对电机磁场与性能的改变,可为混合通风结构电机的设计与运行性能的研究提供参考。

国内外学者针对通风结构对电机电磁性能的影响,主要使用二维有限元计算方法分析研究[6-7]。文献[6]采用二维有限元场-路-运动耦合法,建立混合通风结构分析模型,研究不同通风结构对电机定、转子磁场和气隙磁场的影响,同时计算出了铁心损耗。但是忽略了混合通风结构对电机磁场轴向分布的影响。文献[7]基于二维有限元法,将电机定子铁心径向通风道等效为硅钢片叠压系数,研究定子径向通风道数量对永磁同步发电机的影响。当铁心有效长度不变时,增加径向通风道的数量会使得电机效率降低。该方法忽略了径向通风道边缘漏磁对电机气隙磁场的影响。文献[8]运用三维有限元法研究定子径向通风结构对永磁同步发电机电磁参数的影响。为简化计算模型,只建立定子绕组、定子槽和部分转子,省略了定子轭部和转子轭部。此方法无法对电机整体磁场分布和损耗计算分析。文献[9]运用三维有限元法对含定、转子径向通风结构的十二相感应电机附加损耗计算分析。为简化计算,其模型将转子径向通风道等效为转子铁心叠压系数。此方法忽略了转子铁心分段和转子通风槽板对电机磁场的影响。

目前国内外学者对混合通风结构电机的研究,均无法对其准确分析,为全面反应建立混合通风结构对电机磁场分布以及损耗和性能参数影响,需采用三维有限元计算方法。

本文以6 000 V、4 500 kW中型高压感应电机为例,充分考虑气隙磁场受径向通风道边缘漏磁的影响,建立混合通风结构电机和同计算功率轴向通风结构电机的三维瞬态有限元模型,对样机额定工况进行电磁计算。对比分析建立混合通风结构电机磁场分布特征,计算混合通风结构铁耗、铜耗和转子通风槽板的损耗和主要性能参数,并与轴向通风结构电机参数对比分析。最后,实验证明了分析与计算结果的合理性和准确性,以及混合通风结构对电机电磁性能的影响不可忽略。

1 轴向风路电机建模与磁场分析

本文高压感应电机为变频电机,绕组为Y接,额定工况频率为67 Hz,极数为2,铁心长为640 mm。电机模型主要参数如表1所示。

表1 电机模型主要参数Table 1 Main parameters of motor model

由于该电机采用混合通风结构,电机的气隙磁场沿轴向分布不只是在定转子铁心之间,有少部分气隙磁场分布在没有硅钢片的径向通风道中,转子通风槽板采用Q235A材料,此材料具有导磁和导电性,在电机运行时,产生涡流损耗。传统方法在分析混合通风结构电机时,采用轴向通风结构电机等效混合通风结构电机,默认气隙磁场沿轴向均匀分布,计算模型忽略电机径向通风道以及转子通风槽板。保证计算精度相同,只考虑径向通风结构改变对电机磁场和性能的影响,混合通风结构建立前后均使用三维有限元法分析。为保证电机计算功率不变,需要通过混合通风结构电机的铁心长,等效计算出轴向通风结构电机的有效铁心长[10]。定、转子都具有径向通风道且相互对齐,计算公式为

(1)

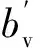
为方便描述,本文简称无径向通风结构电机为轴向风路电机。本文电机极数为2,考虑到电机尺寸较大,同时绕组重复排列,磁场分布具有周期对称性,为节省计算时间以及简化计算,轴向风路电机和混合风路电机三维有限元模型均采用轴向1/2、周向1/2计算模型。电机绕组端部为喇叭口形,其结构是电机中最复杂的部分,但定子绕组端部对电机铁心段磁场影响很小,建立端部模型会极大地增加网格数量和计算时长。省略绕组端部模型,将绕组端部电阻R1d=0.015 22 Ω和端部电抗X1d=0.387 4 Ω计算到模型电路中,减少计算时长。轴向风路电机三维有限元计算模型如图1所示。

图1 轴向风路电机模型Fig.1 Axial wind path motor model

在三维瞬态场中采用的是T,ψ-ψ算法[11-12],低频瞬态磁场麦克斯韦方程组计算式为:

(2)

式中:B为磁通密度;H为磁场强度;σ为电导率。

在涡流区:

(3)

在非涡流区:

▽·μ▽ψ=▽·μHs。

(4)

式中:T为矢量电位;Hs为源电流密度在空间中产生的磁场强度;ψ为标量磁位;μ为磁导率;t为时间。对于变化的磁场在求解三维瞬态磁场时,其棱边上的矢量位自由度采用一阶元计算,而节点上的标量位自由度采用二阶元计算。

对额定工况下的电机进行计算,1.5 s时达到稳定状态,电机磁场分布如图2所示。

图2 轴向风路电机磁通密度分布Fig.2 Magnetic flux density distribution of axial wind circuit motor

从图2可以看出轴向风路电机磁场呈现两极对称分布,电机少量定、转子齿部和轴向通风孔周围磁密大于1.8 T出现饱和。这是由于电机运行时,磁极相对处磁密幅值较大,而定子齿部和转子齿部磁路相对较小,所以出现饱和。转子轭部由于建立轴向通风孔导致电机转子轭部磁路出现局部饱和。

2 混合风路电机建模与磁场分析

2.1 混合风路电机三维有限元建模与磁场分布

为方便描述,本文简称含径向通风结构电机为混合风路电机。混合风路电机三维有限元计算模型如图3所示。

图3 混合风路电机模型Fig.3 Hybrid air circuit motor model

对额定工况下的电机进行计算,1.5 s时达到稳定状态,混合风路电机磁场分布如图4所示。

图4 混合风路电机磁通密度分布Fig.4 Magnetic flux density distribution of hybrid air circuit motor

从图4可以看出混合风路电机磁场呈现两极对称分布,电机转子齿部和定子齿部磁密大于1.8 T出现饱和。轴向通风孔周围磁密在1.8 T附近,局部出现饱和,相较于轴向风路电机,由于建立径向通风结构的影响,定、转子齿部饱和程度更加严重。对电机定、转子铁心轴向中心处做切面,对电机定、转子铁心磁密进行径向和切向分解。径向和切向磁密分布如图5和图6所示。

图5 径向磁密分布Fig.5 Radial magnetic density distribution

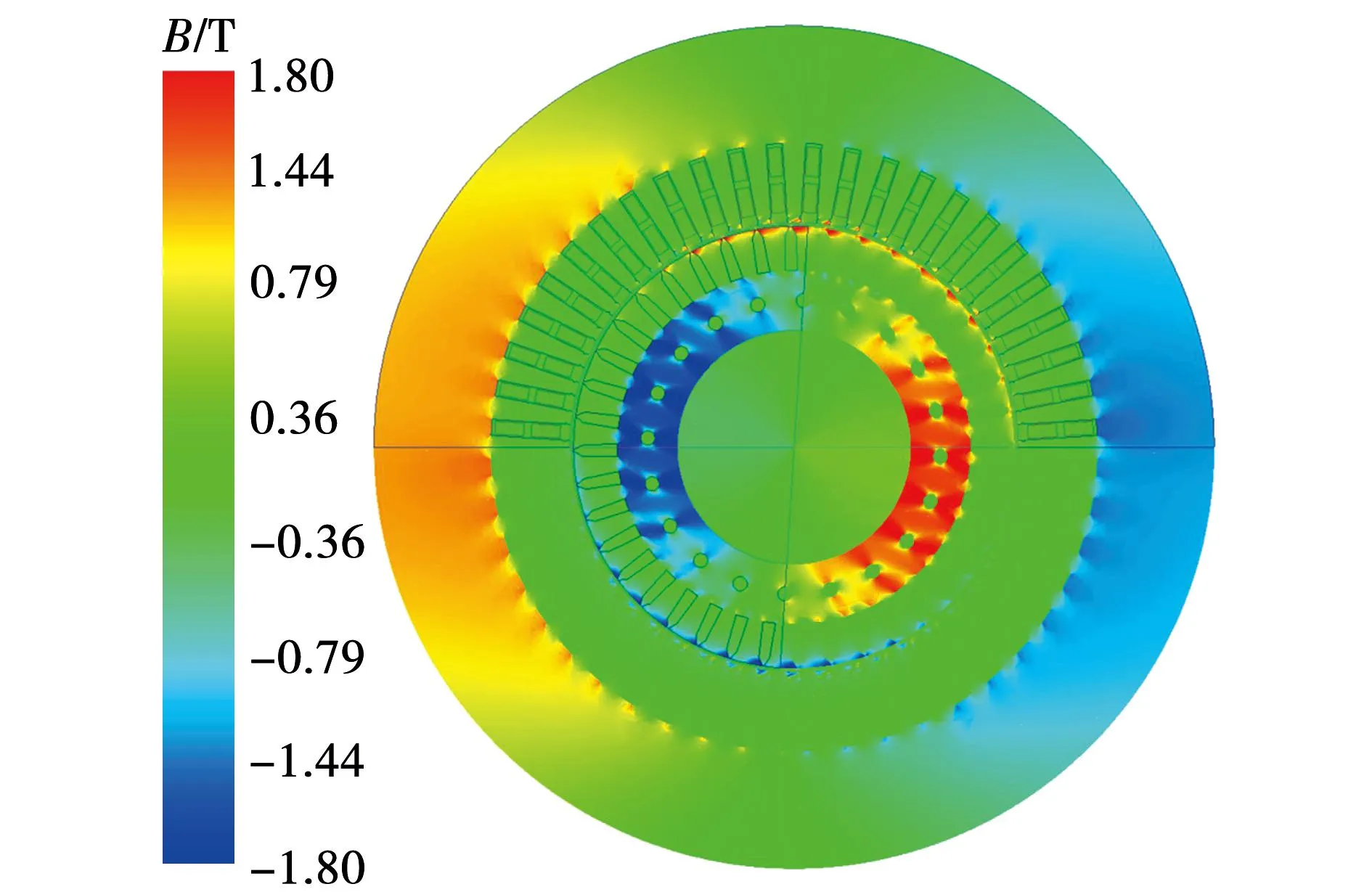
图6 切向磁密分布Fig.6 Tangential magnetic density distribution

从图5和图6可以看出电机定子轭部和转子轭部切向磁密幅值较高,而定子齿部和转子齿部径向磁密幅值较高,所以有必要对电机的定、转子轭部和齿部磁密分别进行分析。

2.2 定转子铁心分析位置的选取

为分析混合通风结构对电机轴向磁场分布的影响,对混合风路电机做轴向切面,如图7所示。

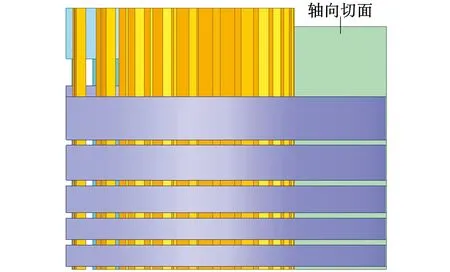
图7 轴向切面Fig.7 Axial section

同时对混合风路电机每段铁心和径向通风道进行编号,作为分析位置,铁心段编号为1～5,径向通风道编号为V1～V4,如图8所示。

图8 混合风路电机铁心编号Fig.8 Hybrid air circuit motor core number

2.3 混合通风结构对电机轴向磁场分布的影响

混合风路电机轴向磁密分布和磁密矢量分布如图9所示。

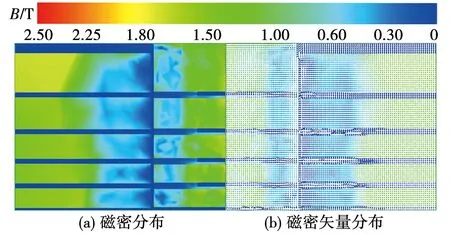
图9 电机轴向磁场分布Fig.9 Axial magnetic field distribution of motor

从图9中可以看出,电机部分磁场分布在定、转子径向通风道内,定、转子轭部附近径向通风道内磁场分布基本沿电机切向方向,而定、转子齿部附近径向通风道磁场分布,相对复杂,方向不唯一,主要有两条路径,一部分沿电机径向方向进入到气隙,另一部分沿电机切向方向进入到电机齿部,这是由于混合通风结构电机铁心分段导致边缘效应。

为对比分析混合通风结构对电机定、转子磁场的影响,分别求取轴向风路电机定子轭、定子齿、转子齿、转子轭磁密均值。由于混合风路电机每段铁心长度不等,分别求取三维电机1～5段铁心的定子轭、定子齿、转子齿、转子轭的磁密均值叠加再求取平均值与轴向风路电机对比,如表2所示。

表2 分析位置磁密均值对比Table 2 Comparison of magnetic density 单位:T

从表2可以看出,混合风路电机定子轭部、定子齿部、转子轭部磁密均值大于轴向风路电机,这是因为混合风路电机实际铁心长比轴向风路电机短,定子铁心处磁路面积更小,使得混合风路电机磁密均值增大。混合风路电机和轴向风路电机转子齿部磁密均值相差不大。

2.4 混合通风结构对气隙磁场的影响

混合风路电机气隙磁场分布如图10所示,气隙磁密沿轴向分布为中间低两端高的趋势,这是由于电机铁心段厚度沿着电机两端到中心逐渐减小,使得气隙磁场随着铁心段厚度减小而降低。

图10 混合通风结构电机气隙磁密波形Fig.10 Hybrid air circuit motor air gap magnetic density waveform

为了研究混合通风结构对电机气隙磁场的影响,对混合风路电机和轴向风路电机轴向气隙磁密进行叠加求平均值的方式,绘制气隙磁密波形。轴向风路电机气隙磁密波形与混合风路电机气隙磁密波形对比如图11所示。

图11 气隙磁密波形对比Fig.11 Air gap magnetic density waveform comparison

对轴向风路电机气隙磁密波形和混合风路电机气隙磁密波形进行波形畸变率计算,得出轴向风路电机气隙磁密波形畸变率为8.07%,混合风路电机气隙磁密波形畸变率为16.8%,即轴向风路电机气隙磁密波形更加趋于正弦。由于定转子开槽,气隙磁场除基波外,还会存在大量的谐波磁场,谐波磁场会在电机运行时产生谐波损耗,影响电机的效率。对两气隙磁密波形进行傅里叶分解,对气隙磁密基波和谐波进行对比分析,如图12所示。

图12 气隙磁密谐波对比Fig.12 Magnetic density harmonic correlation of air gap

从图12可以看出,轴向风路电机气隙磁密基波幅值为0.638 T,混合风路电机气隙磁密基波幅值为0.577 T,在考虑径向通风结构后,电机的气隙磁密基波幅值降低,降幅为9.6%,同时混合风路电机的3次谐波幅值更大。这是因为混合风路电机对比轴向风路电机的实际铁心长更短,使得铁心更加饱和,增大了铁心磁路的磁阻,铁心分得更多的磁压降,为了维持主磁场不变,削弱了气隙磁场。混合风路电机的各次谐波也有不同程度得增加,尤其是39、41、47、49次谐波增加较为明显。39和41次谐波是转子1阶齿谐波,39次谐波幅值为0.133 T,占基波的23.05%,41次谐波幅值为0.128 T,占基波的22.18%。47和49次谐波是定子1阶齿谐波,47次谐波幅值为0.179 T,占基波的31.02%,49次谐波幅值为0.139 T,占基波的24.09%。由此可见,径向通风结构对电机的定、转子和气隙磁场影响较大,不可忽略,同时电机建立径向通风结构不利于电机磁场的分布。

2.5 转子通风槽板磁场分布

混合通风结构电机转子径向通风道处安装通风槽板,用来增加电机的通风散热能力。通风槽板采用的是Q235A材料,此材料具有导磁性。电机在运行时,部分磁场会分布在通风槽板上,转子通风槽板磁场分布如图13所示。

图13 通风槽板磁场分布Fig.13 Magnetic field distribution of ventilation slot plate

从图13中可以看出,通风槽板齿顶处和通风孔周围磁密相对较高,在1.8 T附近。这是由于转子铁心建立轴向通风孔,使得转子轭部铁心出现局部饱和,同时通风槽板和转子铁心紧密接触,使得部分磁场泄漏到转子通风槽板。

3 混合风路高压感应电机损耗计算

3.1 铁心损耗和铜耗计算模型

铁心损耗的计算模型目前广泛使用的是Bertotti三项式模型[13-15],铁心损耗由磁滞损耗和涡流损耗两部分组成,计算公式为

(6)

式中:Bm为铁心磁密;kh、kc、ke分别为磁滞损耗系数、经典涡流损耗系数、异常涡流损耗系数;f为磁场频率。

本文通过有限元法,计算电机额定工况时的铁心损耗。对于任一单元e,假定定子铁心共n个剖分单元,考虑到铁心中磁密在一个时间周期内含有μ次谐波分量,计算铁心损耗公式为

(7)

式中:Brk为磁通密度径向第k次分量幅值;Btk为磁通密度切向第k次分量幅值。

定、转子铜耗的计算方法同样使用有限元计算模型[16],计算公式为:

(8)

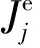
3.2 转子通风槽板涡流损耗计算

通过上文分析,部分磁场分布在转子通风槽板上,通风槽板材料为Q235A,此材料具有导电性,其电导率为5×106S/m。电机在运行时,磁场会在通风槽板感生电流,产生涡流损耗,进而影响电机的效率和温升。所以需要对通风槽板的涡流损耗进行计算。

通过有限元法求解得到一个电周期T内,转子通风槽板涡流损耗平均值Pav[17-18],计算公式为:

(9)

式中:Je(t)为涡流电密;Ve为有限元体积;T为电周期;P(e)(t)为涡流损耗瞬时值。

混合风路电机在额定状态下,转子通风槽板涡流电密分布如图14所示。

图14 通风槽板涡流电密分布Fig.14 Eddy current density distribution

从图14可以看出,通风槽板涡流电密的最大值分布在齿顶处,最高为48 120 A/m2,涡流电密相对较小,通风槽板的涡流损耗主要分布在齿顶处。

4 计算结果分析与实验验证

通过上述方法,计算出混合风路感应电机和轴向风路感应电机额定工况运行时达到稳定状态的结果。将计算后的损耗参数进行对比分析,如图15所示。

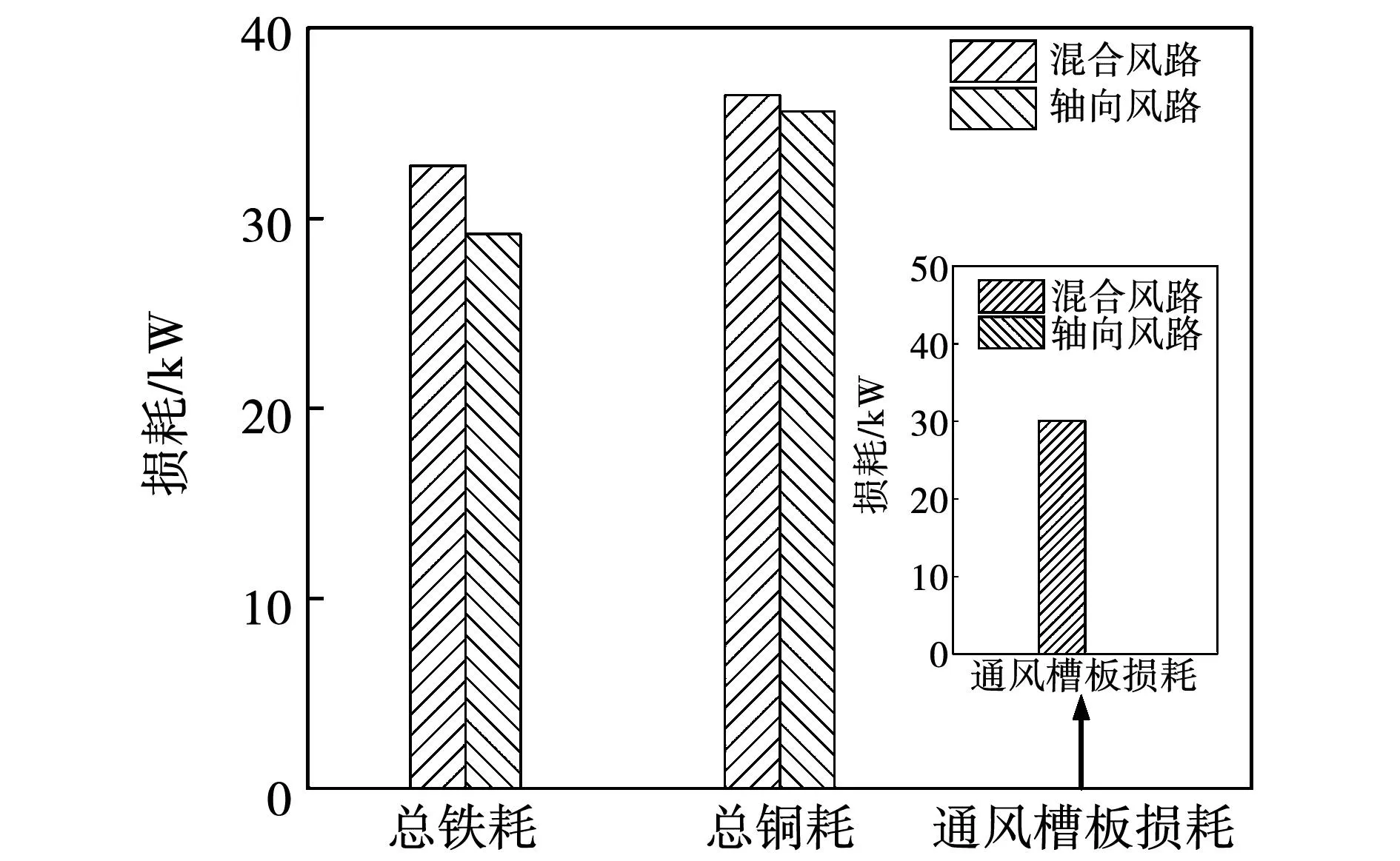
图15 损耗对比Fig.15 Loss comparison

从图15可以看出,混合风路电机总铁耗为32.78 kW,轴向风路电机总铁耗为29.17 kW,损耗相差较大。这是因为电机铁心损耗主要在电机定子铁心产生,铁心损耗与磁密的平方成正比,通过上文分析得到,考虑电机径向通风结构后,电机定、转子轭部和定子齿部磁密增加,使得铁心损耗增大,铁心损耗相较于轴向风路电机增幅11.01%。通过计算,求得混合风路感应电机的9个通风槽板的总涡流损耗平均值为30.1 W,数值较小,这是因为涡流的大小和转子磁场的频率成正比,电机在额定工况运行时,转子磁场的频率f2=sf1,其中s为转差率,定子磁场频率f1=67 Hz,电机在额定运行时转差率s=0.004 97,转子磁场的频率仅为f2=0.333 Hz,所以感应出的涡流电密相对较小,同时通风槽板具有小的体积,使得涡流损耗值相对较小,对电机效率的影响可以忽略不计。混合风路感应电机总铜耗为36.47 kW,轴向风路感应电机总铜耗为35.636 kW,相较轴向风机电机损耗有所增加。这是因为混合风路感应电机考虑径向通风结构后,定、转子铁心实际长度更短,电机在运行时磁路更加饱和,使得漏磁增加,定子电流增大,导致电机铜耗增加。

混合风路电机和轴向风路电机性能参数对比如表3所示。

表3 性能参数对比Table 3 Comparison of loss and performance parameters

从表3可以看出,混合风路感应电机相较于轴向感应风路电机的转矩更小,这是因为感应电机的转矩与气隙磁密的幅值成正比,由于考虑径向通风道,使得电机铁心更加饱和,增大了铁心处的磁压降,削弱了气隙磁场,进而降低电机的电磁转矩。考虑径向通风结构后,混合风路感应电机比轴向风路感应电机铜耗和铁耗更大,混合风路感应电机效率下降了0.19%,功率因数降低了0.006。

4.1 电机温度分布与实验验证

将混合风路感应电机和轴向风路感应电机计算出的损耗结果作为热源带入到温度场中[19],计算出电机温度分布,如图16和图17所示。

图16 轴向风路热源电机温度分布Fig.16 Temperature distribution of axial air path heat source motor

图17 混合风路热源电机温度分布Fig.17 Temperature distribution of heat source motor in mixed air circuit

从图16和图17可以看出,电机温度最高位置在定子槽底,轴向风路感应电机损耗作为热源,电机最高温度为73.6 ℃,混合风路电机损耗作为热源,电机最高温度为75.1 ℃。由于混合风路感应电机损耗计算出的损耗高于轴向风路感应电机的损耗,所以符合温度分布规律。由于铁心损耗和铁心质量成正比,电机的两端铁心段更厚,铁心损耗占比更大,同时更厚的铁心段与冷却气的热传递不够充分,导致电机铁心局部出现温度较高的情况。

为了保证简化模型和计算分析的合理性和准确性,对电机做了温度测量。图18为本文实验样机。

图18 实验样机Fig.18 Test machine

在实验过程中,将铂金电阻放置在3个定子槽中,测量电机定子侧上下绕组层间的绝缘温度。铂金电阻的阻值会随温度变化而变化。当电机稳定运行时,电机内温度升高,紧贴在绝缘层间的铂金电阻阻值发生改变,通过铂金电阻阻值与其温度的对应关系,可以得到实验测量温度。铂金电阻、铂金电阻安装位置和电机测温位置,如图19和图20所示。

图19 铂金电阻安装位置Fig.19 Platinum resistance installation position

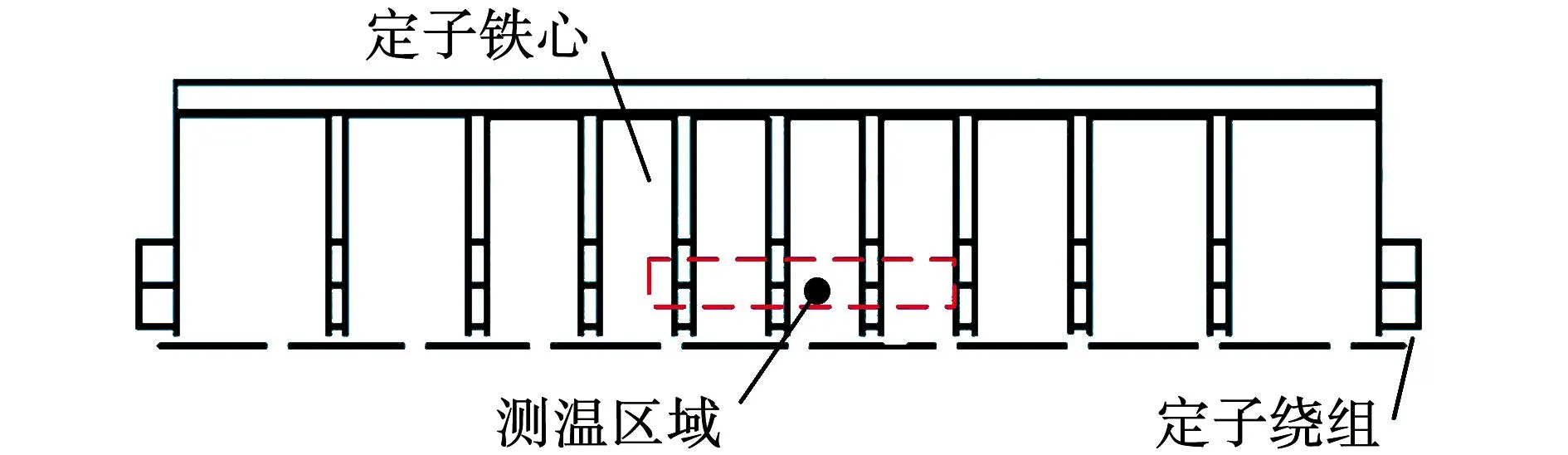
图20 电机测温位置Fig.20 Motor temperature measurement position

本实验共测得5组数据,舍弃最大值79.9 ℃和最小值68 ℃。层间绝缘仿真数据与实验测量结果对比如图21所示。

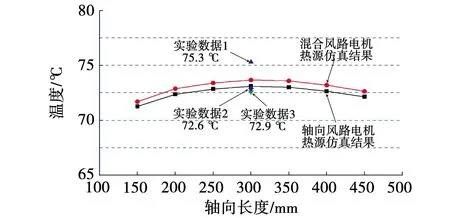
图21 仿真结果和实验结果对比Fig.21 Comparison of calculation results and test results

通过图21对比可以看出,3组实验数据平均值为73.6 ℃,轴向风路电机损耗作为热源仿真平均值为72.48 ℃,误差为1.52%,混合风路电机损耗作为热源仿真平均值为73.01 ℃,误差为0.8%,对比结果证明了本文混合通风结构电机三维有限元计算方法的准确性以及混合通风结构对电机电磁场性能的影响较大,同时证明了在设计和分析混合通风结构电机时,需考虑径向通风结构,不可用轴向通风结构电机等效分析。

5 结 论

本文分别建立混合风路高压感应电机模型和轴向风路高压感应电机模型,对比分析了混合通风结构对电机磁场分布和性能参数的影响,同时对其主要性能参数和损耗进行计算,运用实验验证了对比计算分析的精确性和合理性。通过对计算结果的分析得到以下结论:

1)为对比分析建立混合通风结构对感应电机磁场和损耗的分布影响,建立了含转子通风槽板的混合风路感应电机和轴向风路感应电机三维有限元模型,此模型能够计及混合通风结构和转子通风槽板对电机磁场和损耗的影响。同时绕组端部对电机直线段影响很小,避免建立复杂端部模型,减少计算时长,将端部电阻和端部电抗计算到模型电路中。

2)运用三维有限元法计算得出,混合风路感应电机定子轭部磁密均值为0.909 T、定子齿部磁密均值为0.911 T、转子齿部磁密均值为1.306 T、转子轭部磁密均值为1.077 T。轴向风路感应电机定子轭部磁密均值为0.734 T、定子齿部磁密均值为0.851 T、转子齿部磁密均值为1.301 T、转子轭部磁密均值为0.872 T。相比之下,考虑混合通风结构时定、转子铁心磁密均值更大。由于磁路更加饱和导致气隙磁场削弱,降低了电机电磁转矩。混合通风结构对感应电机磁场分布的影响不可忽略。

3)通过三维有限元法计算得出转子通风槽板上的涡流损耗为30.1 W,相对较小,对电机效率的影响可以忽略,铁心损耗相较于轴向风路电机增加3.61 kW,增幅为11.01%,对电机的效率和温升影响不可忽略。通过实验验证了简化模型和分析结果的准确性和合理性,研究混合通风结构感应电机时,需考虑径向通风结构对电机电磁性能的影响。