基于离散域改进PIR控制的PMSM电流谐波抑制策略

王智杰, 蒋哲, 李争, 张驰

(1.河北科技大学 电气工程学院,河北 石家庄 050018; 2.中国科学院宁波材料技术与工程研究所,浙江 宁波 315201)

0 引 言

永磁同步电机(permanent magnet synchronous motor,PMSM)运行过程中一些因素会导致定子电流中产生丰富的电流谐波,如逆变器的死区时间和管压降等非线性因素、电机的齿槽效应和绕组分布形式等[1-3],使得电流波形发生畸变,导致电机损耗和电磁噪声等不利影响进一步增大。

比例谐振控制是电流谐波抑制算法中的一种常用方法,应用领域较为广泛,许多学者对其进行研究。陈哲等[4]提出一种电流环的比例谐振型自抗扰控制,在扩张状态观测器中引入比例谐振项,可以在实现d-q坐标系电流完全解耦的基础上有效抑制各类电流谐波。ZHOU Sizhan等[5]对比分析了同步旋转坐标系和静止坐标系解耦对比例谐振控制性能的影响,在传统比例谐振控制中加入耦合项可以改善电流跟踪的暂态响应,降低谐振控制器对频率变化的敏感性。李佳等[6]提出基于准比例谐振控制的有源电力滤波器,实现对各种频率分量协调控制,补偿电网中的高次谐波电流。VIDAL A等[7]提出一种评估和优化比例谐振电流控制器暂态响应的方法,该方法基于零极点图对误差信号传递函数根的研究,设置最佳增益以实现快速且无振荡的瞬态响应。

比例谐振控制的谐振增益值与谐波电流抑制效果有关,如果设计不合理会导致系统不稳定,因此控制器的参数设计部分是至关重要的一环。游小杰等[8]基于Nichols图提出一种增益设计方法,通过优化调整时间和超调选取最终参数,重点关注了控制器的动态响应,并没有具体分析不同工况时控制器参数对电流谐波含量的影响。魏艺涵等[9]通过电流环连续域传递函数计算系统最佳阻尼比来确定比例增益和谐振增益,但未分析不同工况时参数变化对系统稳定性的影响。姜燕等[10]通过对比分析不同参数的频域特性和零极点分布,确定合适的控制参数,这种分析方法与实际系统有一定的差距,只能作为初步分析,并且也没有考虑负载变化的影响。HANS F等[11]为了在稳定裕度和较小的稳态控制误差之间取得良好的折衷,提出一种递归调整控制器积分增益的方法,但这种系统稳定性分析方法依旧基于传递函数频域分析。

本文通过将比例谐振控制器应用在同步旋转坐标系,与PI控制器并联构成比例积分谐振(proportional integral resonance,PIR)控制器,实现对5、7次电流谐波的抑制,提出一种离散域谐振控制器离线参数表设计方法,结合滞环控制和模糊逻辑方法,实现谐振增益离线表稳定切换。为解决双线性变换离散化产生的问题,引入预修正双线性变换法,解决高频偏移现象。

1 基于谐振控制器的电流谐波抑制

1.1 谐波分析

由于逆变器存在死区效应和管压降等非线性因素,在电机运行过程中,逆变器输出电压波形发生畸变。对逆变器输出平均误差电压进行傅里叶分解,表达式[12-13]为

(1)

从傅里叶分解结果可以看出,逆变器输出电压存在3次、5次、7次等奇次谐波,当电机绕组为星型连接时,电机电流主要表现为6k±1(k=1,2,3,…)次谐波[14-15],并且谐波幅值随着谐波阶数升高而减小,因此本文主要针对谐波含量较为丰富的5、7次电流谐波进行研究。

根据坐标变换原理,三相电流中6k±1次谐波分量在旋转坐标系下表现为6k次谐波分量,通过降低同步旋转坐标系中6次电流谐波含量,来实现抑制永磁同步电机5、7次电流谐波的目的。

1.2 电流环连续域分析

根据内模原理,在同步旋转坐标系下实现电流谐波的零稳态误差跟踪控制,控制器内部需要含有一个交流信号的内模[16]。为了进一步改善转速波动对谐振控制器在谐振频率点的影响,得到谐振控制器表达式[17]为

(2)

式中:Kr为谐振增益,与电流谐波抑制能力和系统稳定性有关,Kr越大,电流谐波抑制效果越好,但需要考虑增益值对系统稳定性的影响;ω0为谐振角频率;ωc为谐振控制器带宽。

以q轴为例,基于PIR控制的电流环控制框图如图1所示。为研究谐振参数变化对系统性能的影响,以图1控制系统进行频域分析,选择电流环各环节参数如表1所示,得到不同谐振增益时电流环开环频域特性如图2所示。

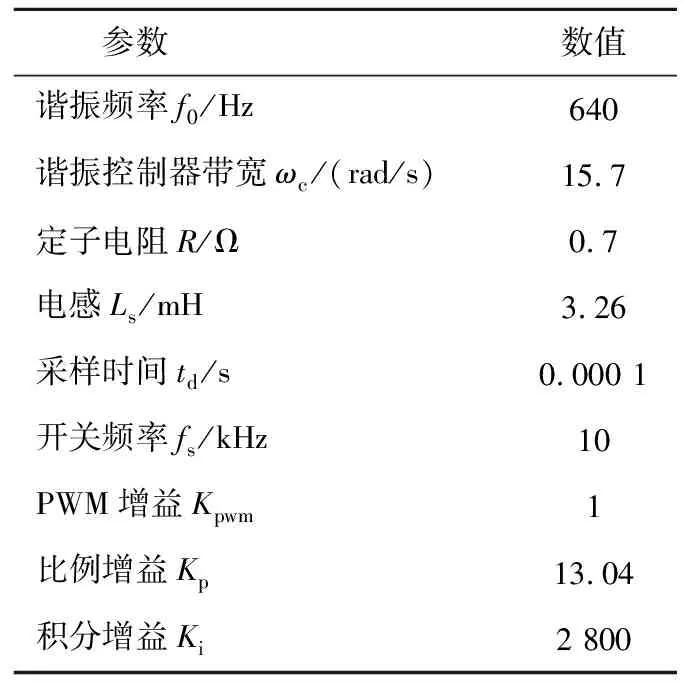
表1 电流环参数Table 1 Parameters of current loop

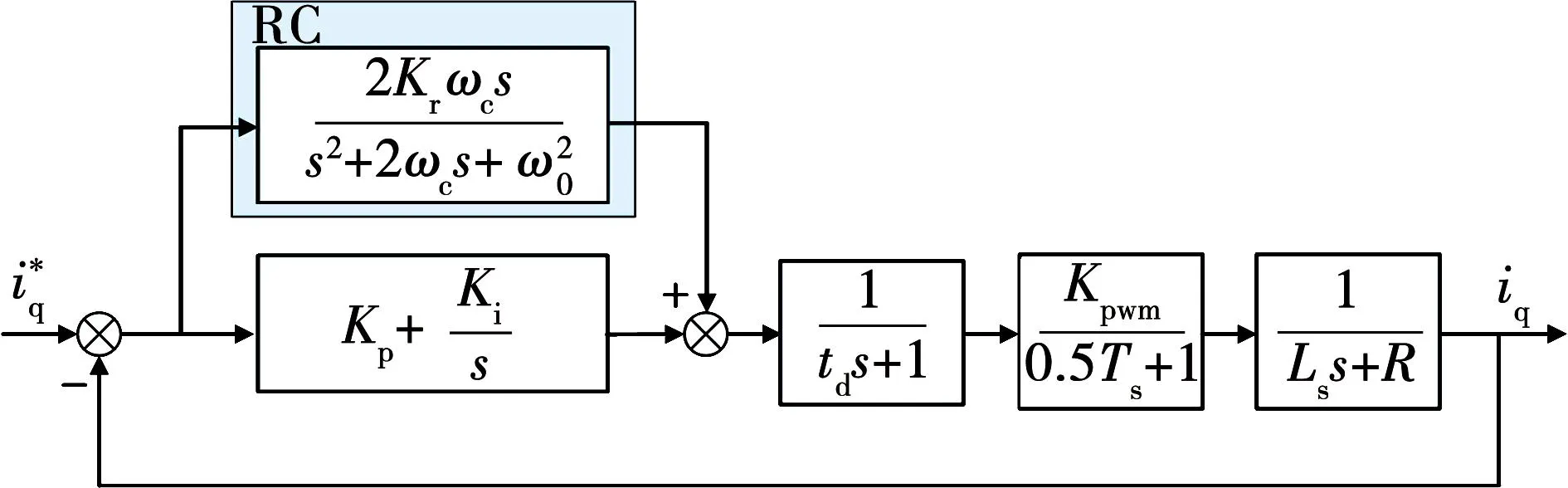
图1 q轴电流环控制框图Fig.1 Control block diagram of q axis current loop

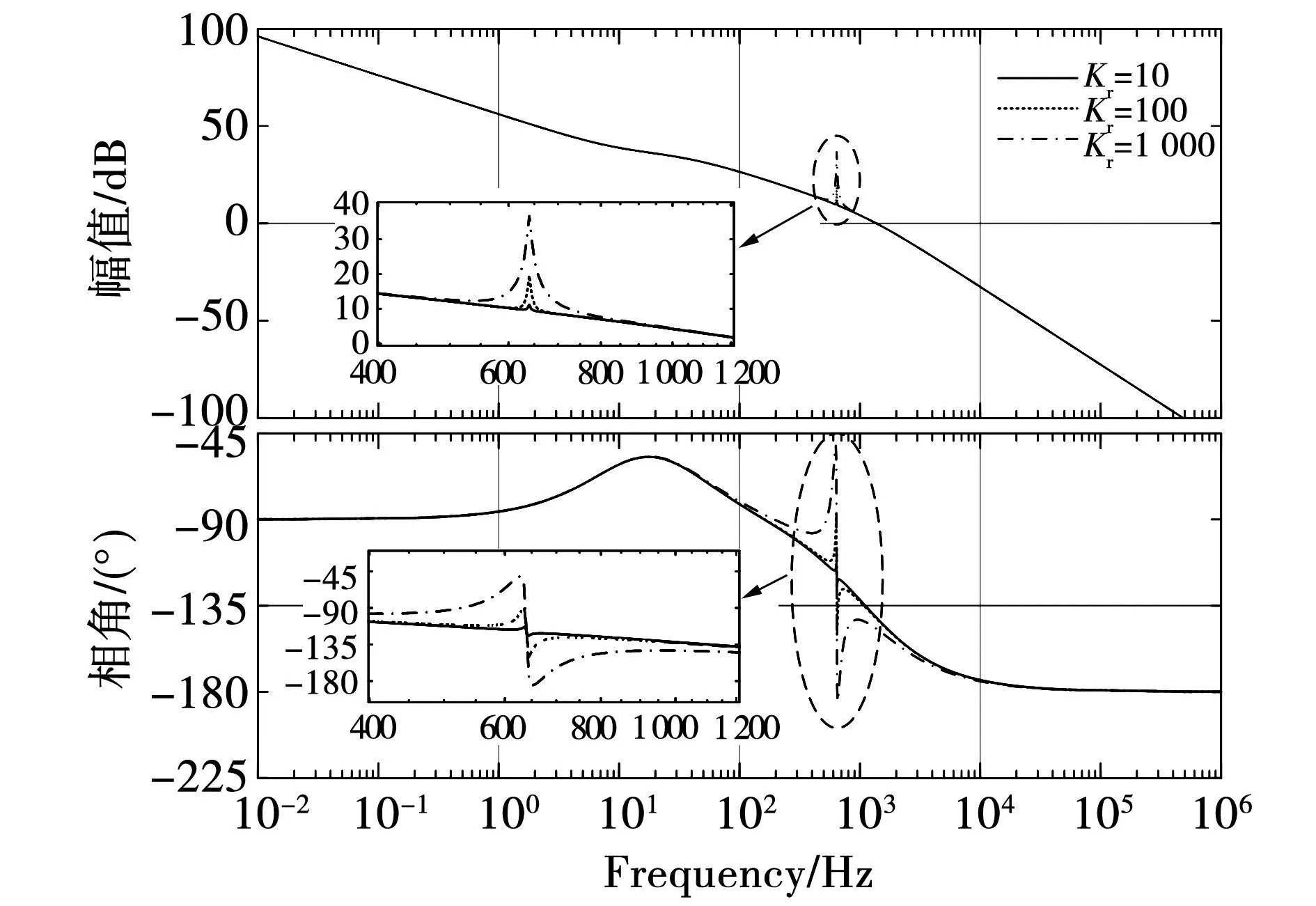
图2 电流环频域特性图Fig.2 Current loop frequency domain characteristic diagram

从电流环频域特性看出,谐振增益Kr越大,谐振频率处幅值越大,电流谐波抑制作用越明显。由于未考虑不同转速时谐振增益变化对系统稳定性的影响,基于连续域的频域分析具有一定的局限性,并且实际控制系统为数字控制器,因此需要在离散域进一步分析。

1.3 谐振控制器离散化

为便于数字控制系统实现,需要对谐振控制器离散化处理,传统双线性变换公式[18]为

(3)

以转速1 000 r/min为例,理论计算谐振频率fr=ω0/2π=800 Hz,而传统双线性变换离散化后实际谐振频率freal计算公式为

(4)

式中Ts为采样周期,可以发现离散化后会导致谐振频率点发生偏移,严重影响谐波电流抑制效果,且偏移量与转速和采样频率有关。

为解决离散化产生的谐振频率偏移问题,本文提出一种预修正双线性变换方法,其s域到z域变换[19]为

(5)

代入式(3)得到谐振控制器离散域表达式为

yr(k)=H1e(k)+H2e(k-2)-L1yr(k-1)-L2yr(k-2)。

(6)

式中:yr(k)为当前时刻谐振数字控制器输出;e(k)为当前时刻误差电流值;系数H1、H2、L1、L2分别满足:

(7)

改进双线性变换法前后的频域特性对比如图3所示,预修正双线性变换离散化后谐振频域值与理论计算值一致,解决了谐振频率点偏移问题。

2 离散域稳定性分析

永磁同步电机d-q同步旋转坐标系中定子电压方程为:

(8)

式中:ud、uq分别为d轴和q轴电压;id、iq分别为d轴和q轴电流;Ld、Lq分别为d轴和q轴电感;R为电机定子电阻;ωe为电机电角速度;φf为永磁体磁链,离散化后得到永磁同步电机离散方程为

(9)

式中:Ts为采样周期;id(k)、iq(k)分别为当前时刻d轴和q轴电流值;ud(k)、uq(k)分别为当前时刻d轴和q轴电压值;id(k+1)、iq(k+1)分别为下一采样周期时刻d轴和q轴电流值;A和B的表达式为:

为进一步分析离散域电流环系统稳定性,选择电流环状态变量为:

(10)

得到离散域差分方程状态空间形式为

(11)

式中:u(k)、y(k)分别为电流环当前时刻输入和输出;a1=m2/m3,a0=m1/m3,系数分别满足:

(12)

(13)

(14)

其中:Ls=Ld=Lq;KPI为PI控制器等效增益。

ATZA-Z=-Q。

(15)

通常取正定对称矩阵Q为单位矩阵,化简求解式(15),得到矩阵Z各系数表达式满足:

(16)

其中系数z11、z12、z21、z22满足:

(17)

进一步化简求解,得到满足系统稳定条件的谐振增益与转速之间的关系为:

(18)

式中a0、a1为谐振增益Kr和转速的隐函数,联立即可求得不同转速对应的谐振增益最大值,利用数学工具进一步求得满足式(18)的最大谐振增益理论计算值与转速的关系曲线如图4所示,可以看出,转速越高,对应谐振增益越小。

图4 谐振增益与转速关系曲线Fig.4 Curve of resonance gain and rotational speed

3 参数动态整定

3.1 负载扰动分析

永磁同步电机转速环简化控制框图如图5所示,突加减负载过程中需要考虑负载扰动对转速波动的影响,从负载转矩输入到输出转速的闭环传递函数为

(19)

式中:Kf=1.5Pnφf;J为转动惯量;Giclose为电流环闭环传递函数;Kp、Ki分别为转速环PI控制器比例增益和积分增益,由于二阶闭环传递函数稳定性条件为特征方程系数均大于0,因此在电流环稳定的前提下,负载扰动对转速波动的影响只与转速环PI控制器参数有关[21]。

3.2 调制比分析

根据定子电压方程式(8)可以看出,由于永磁同步电机反电动势和负载电流的影响,使得不同工况下的定子电压值ud、uq发生变化,从而导致空间矢量脉宽调制的调制比大小不同,如图6和图7所示。为此,本文以调制比m为约束条件,保证系统可靠稳定运行,调制比计算公式为:

(20)

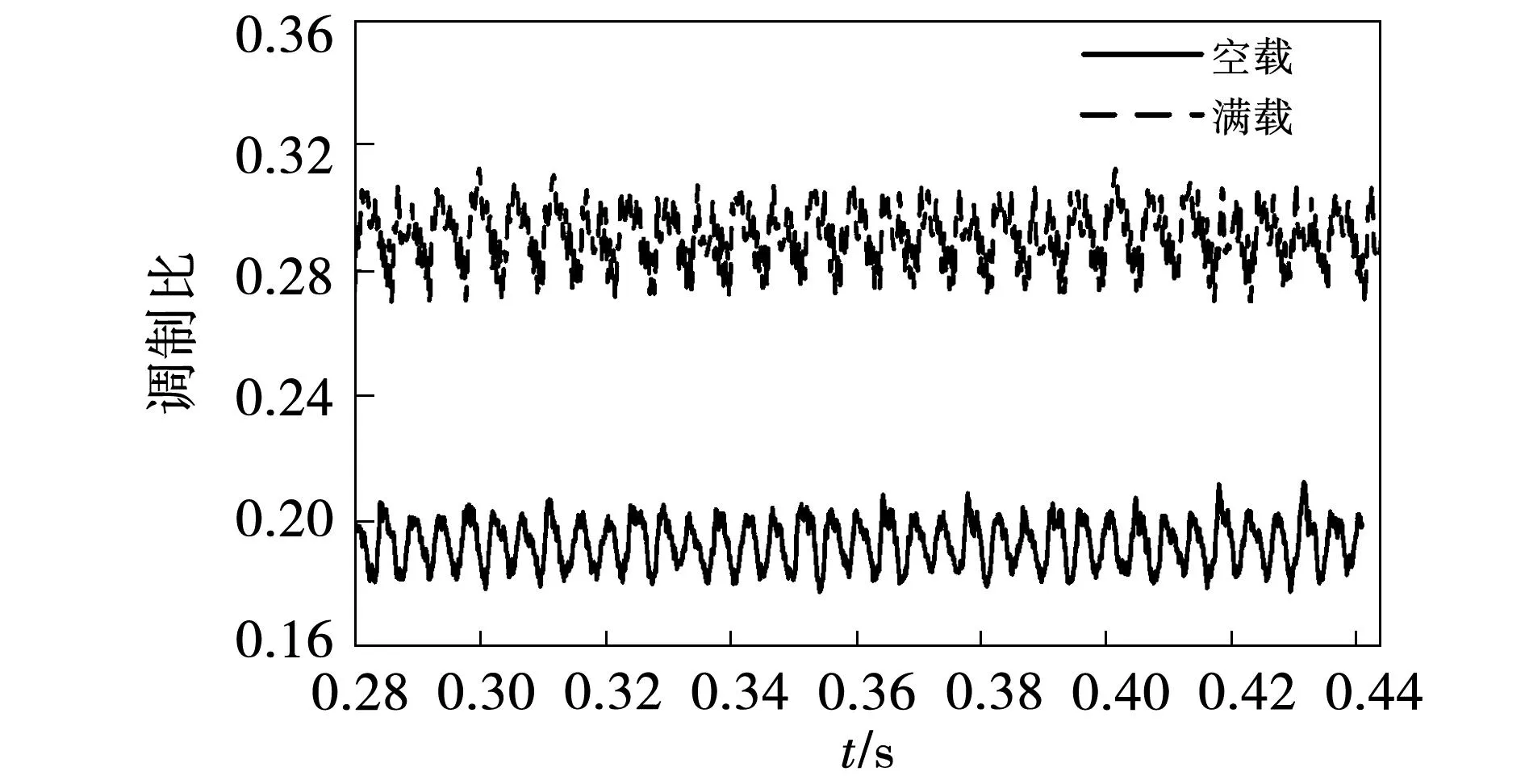
图6 转速200 r/min调制比波形Fig.6 Modulation ratio waveform at 200 r/min

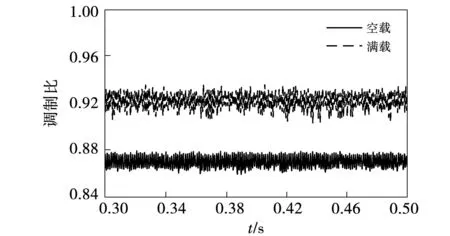
图7 转速1 000 r/min调制比波形Fig.7 Modulation ratio waveform at 1 000 r/min

(21)

式中:θe为电机电角度;Udc为直流母线电压。

综上所述,本文在满足调制比约束的前提下,构建不同转速工况的谐振增益离线表,确定谐振增益最大值,实现不同转速区间的谐波抑制效果最优,其中转速全频段以20 Hz为间隔被划分为各个转速区间,每个转速区间对应满足系统稳定的谐振增益值。

3.3 谐振参数在线切换

由于谐振增益切换过程为分段控制,为了谐振增益在不同转速区间的切换更平滑稳定,本文引入滞环控制算法,研究不同转速工况下的谐振增益切换过程,滞环切换示意图如图8所示,其中:Kri(i=1,2,3,4,5)对应不同转区间谐振增益值;Vj(j=1,2,…,8)对应不同转速区间的速度比较值。

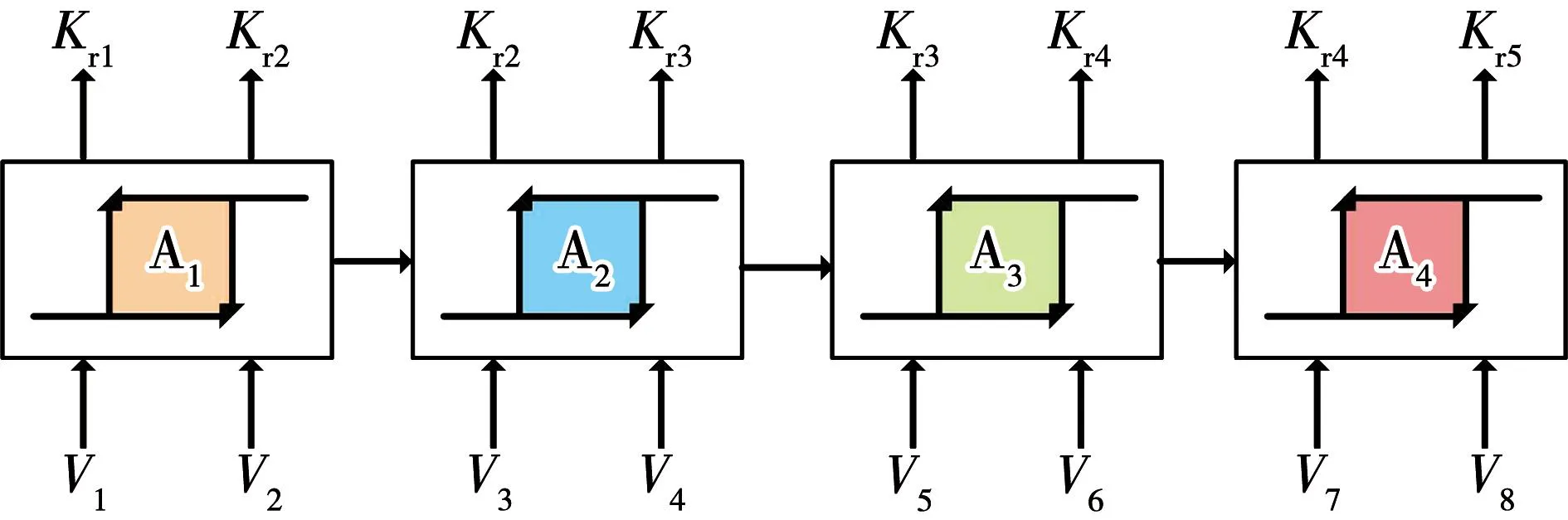
图8 谐振增益切换示意图Fig.8 Schematic diagram of resonance gain switching

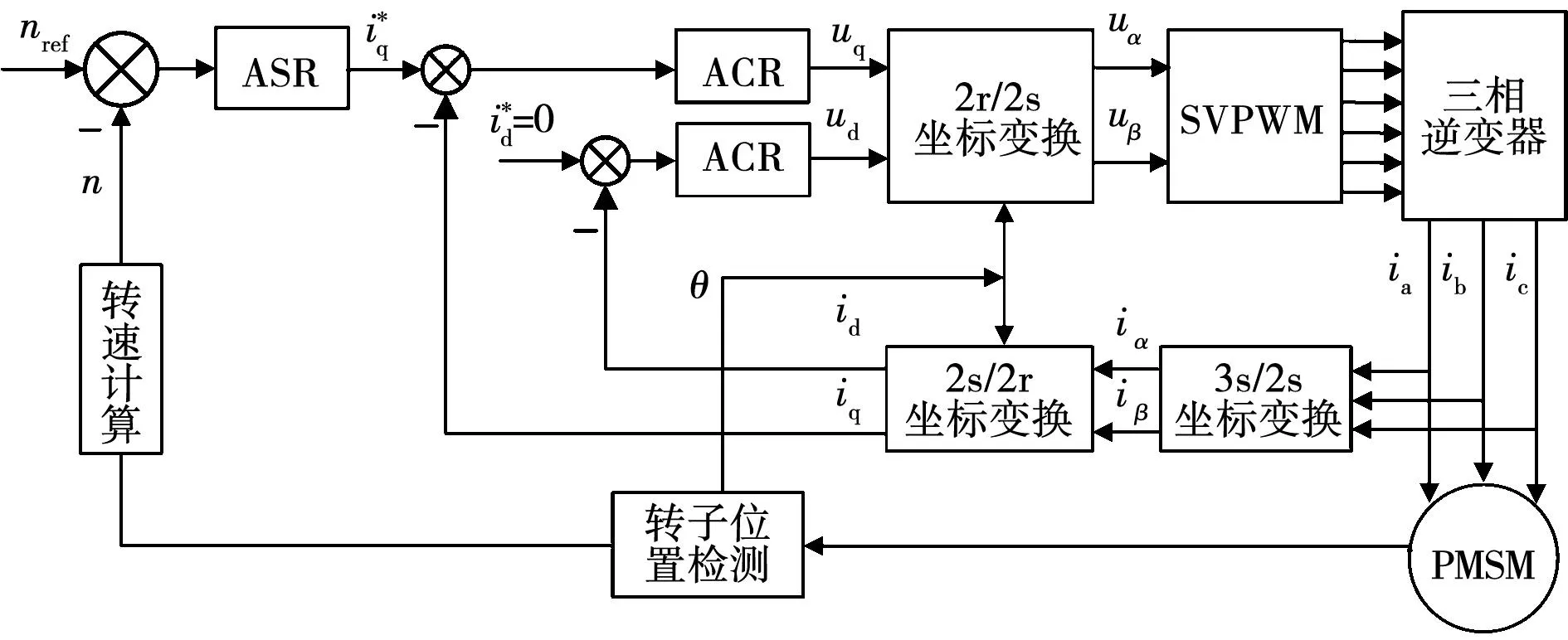
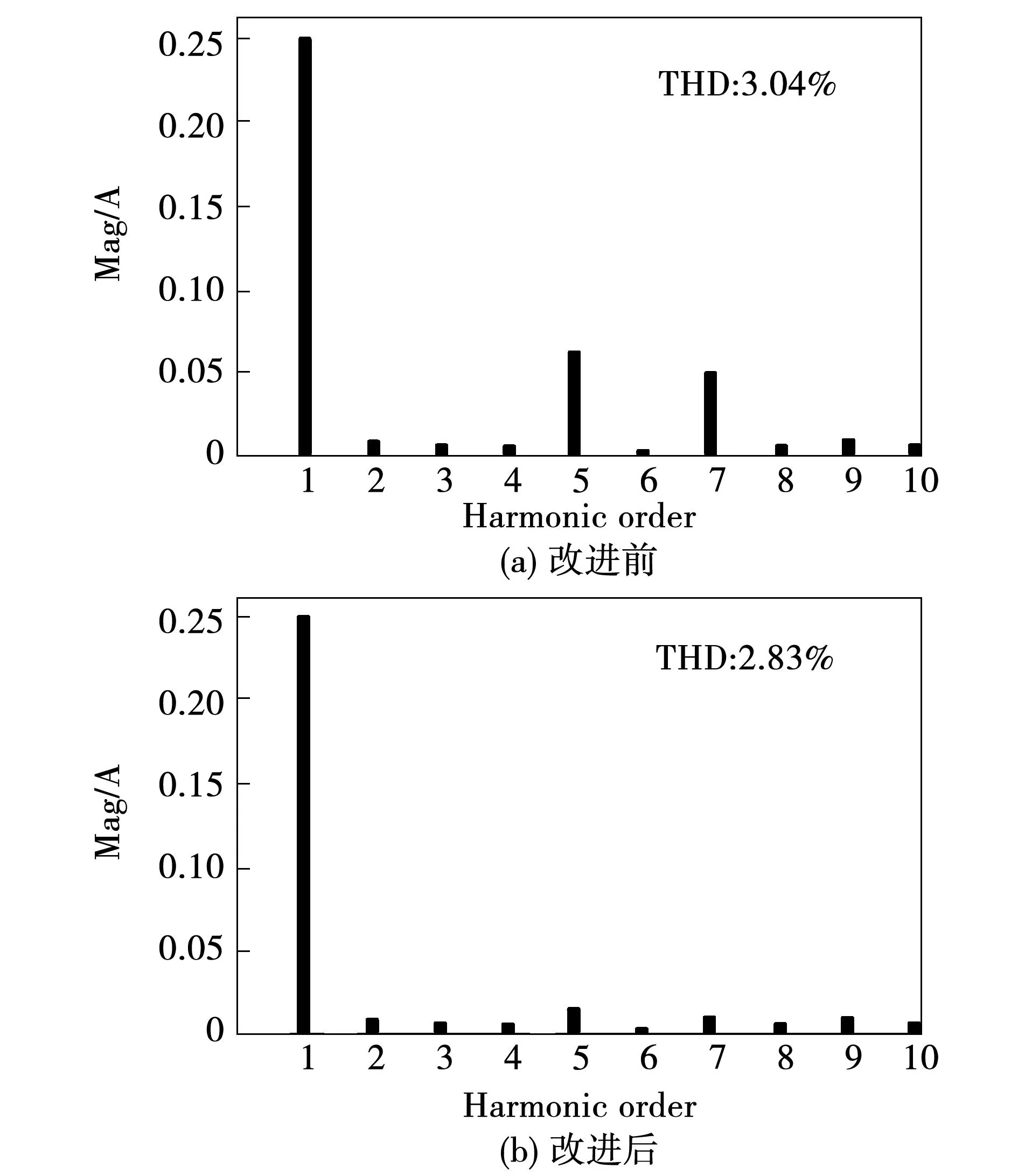
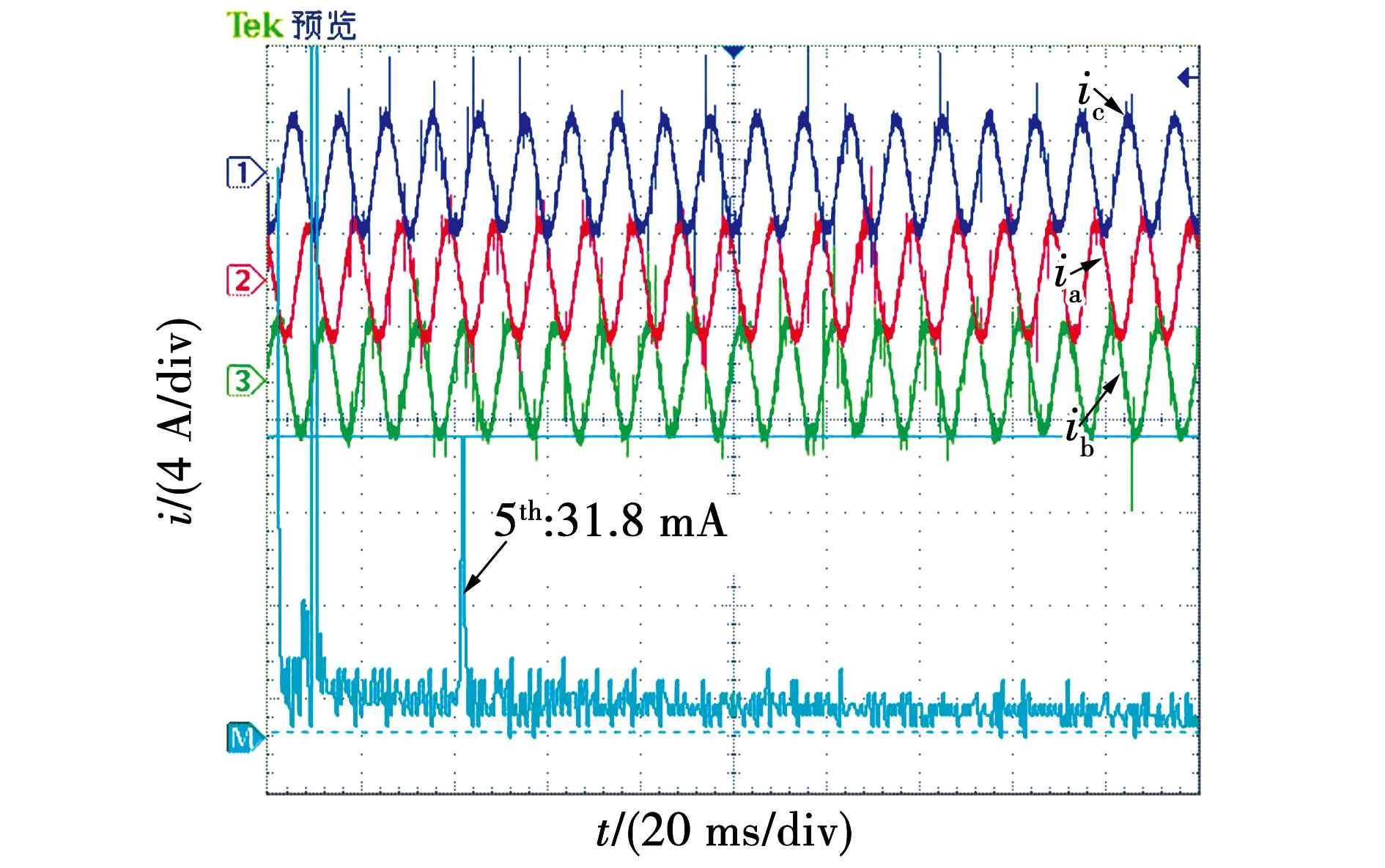
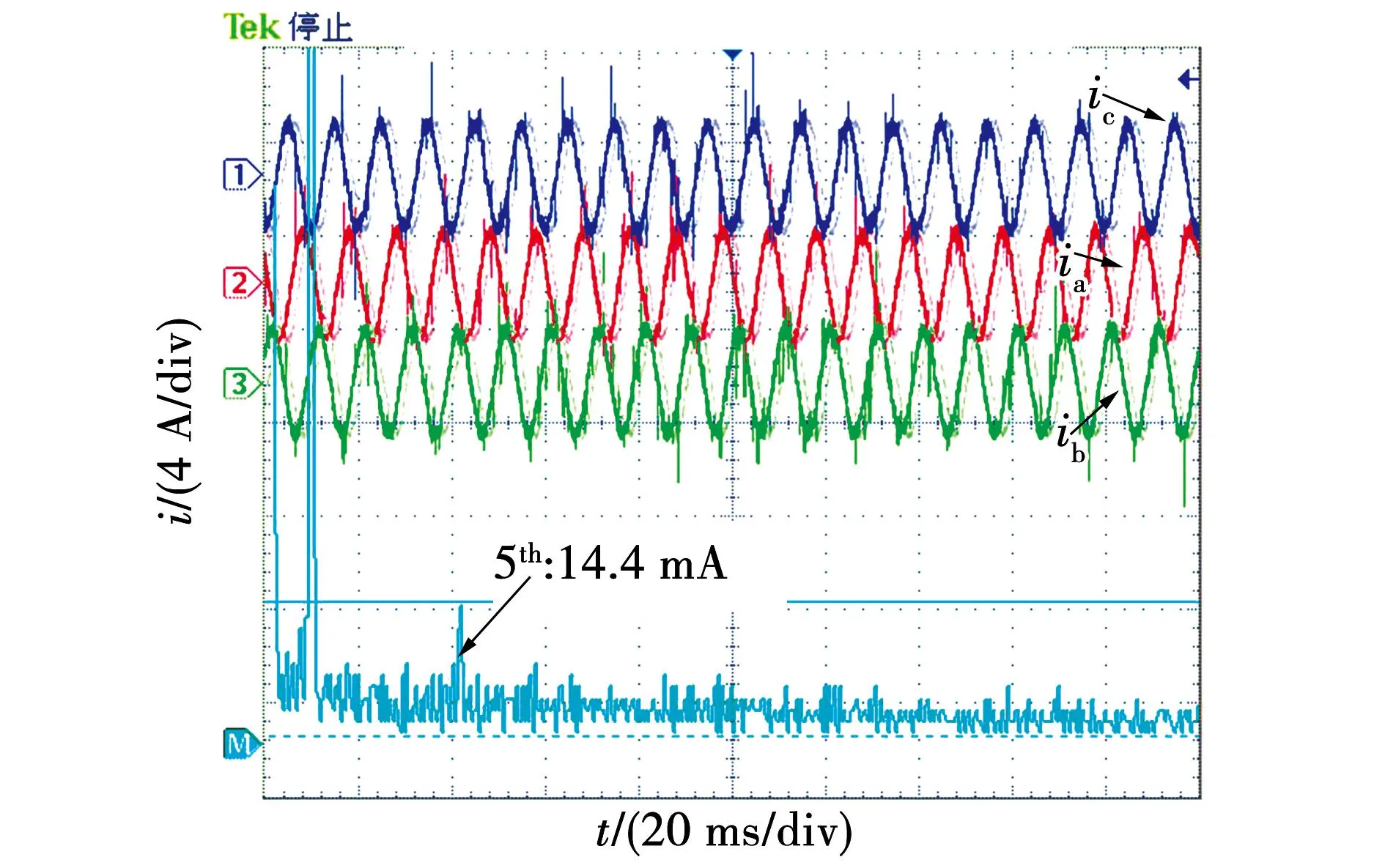
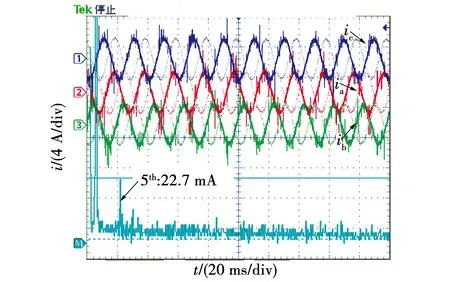
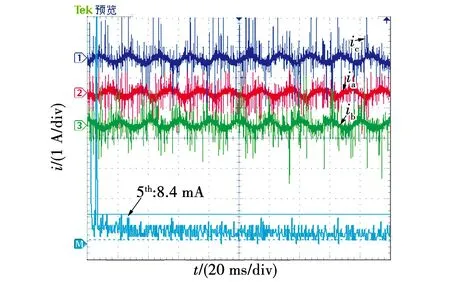
以A1和A2两个子模块为例,进一步解释模块之间速度切换关系。在转速切换点附近设置滞环回路差值ΔV1=V2-V1,电机速度反馈值VfbV2且VfbV1,始终保持输出Kr2,只有当Vfb

4 仿真与实验验证

4.1 仿真验证

为验证上述基于离散域改进PIR控制的电流谐波抑制算法的正确性,搭建基于表2电机参数的仿真模型,其中,转速环控制器(automatic speed regulator,ASR)为PI控制,电流环控制器(automatic current regulator,ACR)为PIR控制,控制框图如图9所示。

表2 PMSM控制系统参数Table 2 Parameters of PMSM control system

图9 控制框图Fig.9 Control block diagram

以转速600 r/min、额定负载为例,加入谐振控制算法前后三相电流快速傅里叶变换(fast Fourier transform,FFT)分解对比如图10所示。从对比结果来看,5次谐波幅值从0.3 A下降为0.02 A,下降了93.3%,7次谐波幅值从0.2 A下降为0.01 A,下降了95%,因此可以证明谐振控制器对5、7次电流谐波有明显的抑制效果。

以转速1 000 r/min额定负载工况为例,加入谐振控制前后三相电流波形如图11所示,与电流谐波抑制前相比,三相电流正弦度有明显改善,几乎看不到三相电流峰值处的平顶现象和过零点的畸变现象,三相电流正弦度更好。

图11 加入谐振控制器前后三相电流波形Fig.11 Three phase current waveform before and after added resonance controller

根据理论分析,如果谐振增益固定不变,高速时,谐振数字控制器输出发散,造成系统不稳定;低速时,则导致电流谐波抑制效果下降。以转速400 r/min为例,优化参数整定方法前后三相电流FFT分解结果对比如图12所示。优化前,5次谐波幅值为0.065 A,7次谐波幅值为0.05 A;而优化后,5次谐波幅值为0.015 A,下降了76%,7次谐波幅值为0.01 A,下降了80%,电流谐波抑制效果有明显提升。

图12 改进谐振控制器前后三相电流FFT分解对比图Fig.12 Comparison diagram of three phase current FFT decomposition before and after improved resonance controller

4.2 实验验证

为了进一步验证提出的基于改进PIR控制的电流谐波抑制算法,以额定功率为2 kW的永磁同步电机进行实验,搭建如图13所示实验平台进行验证,永磁同步电机参数如表2所示。

图13 实验平台Fig.13 Experiment platform

为了对比验证所提出的基于离散域改进PIR算法抑制电流谐波的效果,在频率100 Hz、对应转速750 r/min、负载转矩5 N·m下,传统固定谐振增益和本文提出的改进PIR算法的对比结果如图14和图15所示。

图14 在750 r/min、固定增益下三相电流和谐波分析Fig.14 Three-phase current and harmonic analysis at 750 r/min and fixed gain

图15 在750 r/min、变增益下三相电流和谐波分析Fig.15 Three-phase current and harmonic analysis at 750 r/min and varying gain

由于要求转速在全频段内均稳定可靠运行,根据实验测试,谐振增益取固定值Kr=150,此时5次谐波幅值为31.8 mA,7次谐波抑制效果较好;若根据离线切换表来确定谐振增益,通过实验测试取值Kr=400,如图15所示,此时5次谐波幅值进一步下降为14.4 mA,且电流波形也有明显改善。

为了验证不同转速下所提出离散域改进PIR算法的效果,进一步地,在频率50 Hz、对应转速375 r/min、负载转矩5 N·m下对比,结果如图16和图17所示。在谐振增益取值Kr=400时,5次谐波为22.7 mA,7次谐波为10.8 mA;若谐振参数为变增益值,根据实验测试取值Kr=750,5次谐波幅值进一步下降为12.6 mA,由于7次谐波已接近最小值,因此下降并不明显。因此与图14对比发现,不同转速下变谐振增益取值可进一步优化电流谐波抑制效果。

图16 在375 r/min、固定增益下三相电流和谐波分析Fig.16 Three-phase current and harmonic analysis at 375 r/min and fixed gain

图17 在375 r/min、变增益下三相电流和谐波分析Fig.17 Three-phase current and harmonic analysis at 375 r/min and varying gain

图18为采用所提的方法且Kr=750、频率50 Hz、对应转速375 r/min,空载时电流波形和谐波分析,由于负载较轻,电流波形出现明显的毛刺,但FFT结果显示,此时幅值最大的5次谐波为8.4 mA,且继续改变谐振增益,效果并不明显,可以看出,此时各次谐波含量已接近最小。与图14及图15对比可知,采用所提出的基于离散域改进PIR算法在负载发生突变扰动时,系统可以稳定可靠运行且仍具有良好的谐波抑制效果。

图18 在375 r/min、空载下三相电流和谐波分析Fig.18 Three-phase current and harmonic analysis at 375 r/min and no load

5 结 论

本文为抑制PMSM驱动系统中5、7次电流谐波,在同步旋转坐标系下加入谐振控制器,结合PI控制构成PIR控制器。文中分别给出了电流环连续域和离散域分析过程,改进后的双线性变换方法解决了谐振频率偏移问题,改善了谐波抑制效果。提出基于调制比约束的谐振增益设计方法,通过离线方式确定不同转速工况的参数切换表,结合滞环控制实现不同转速区间的谐振增益在线切换。仿真和实验结果表明,所提出的方法在确保系统运行稳定的前提下,5、7次电流谐波抑制效果更优,且具有较好的实时性和参数适应性,便于工程实现和应用。