永磁电机电磁振动及变开关频率振动抑制技术试验探究
2024-01-18洪剑锋曹君慈刘亚静
洪剑锋, 曹君慈, 刘亚静
(北京交通大学 电气工程学院,北京 100084)
0 引 言
永磁同步电机由于高功率密度而易实现轻量化,广泛应用到宝马、特斯拉、日本Toyota Prius、比亚迪、精进电动等主流品牌电动汽车,是当前最主流的一类电动汽车驱动电机。变频器供电的车用电机系统振动和噪声成为汽车主要的电磁振动噪声源[1]。近年来,国内外学者针对车用永磁电机的电磁振动噪声问题开展了大量研究,取得了一定成果。
针对变频器下的电机振动噪声问题,经过各国学者的深入研究,已经取得了一些实质性的成果,并总结了一些通用性的规律[2-5]:变频器引入会增加电机气隙中高次谐波磁场和开关频率相关的电磁力和电磁振动。定子磁场的主要谐波频率满足关系:fk=k1fs±k2f0,其中k1和k2为奇偶性相异的正整数,例如fs+2f0、fs-4f0…。变频器供电时主要增加的激振力由基波磁场与k次谐波电流产生基波磁场相互作用产生,阶数为0阶或2p阶,频率fn=k4fs±k5f0,其中k4和k5为奇偶性相同的正整数,例如fs+f0、fs-3f0…。其中,fs是载波频率,f0是电机基波频率。变频器供电的永磁电机振动噪声频率至少增加5 dB[6]。
致力于变频器驱动电机时带来的一系列振动问题的解决,各国学者都付出了巨大的努力,归结起来,总共有如下几种方案:
1)加装滤波器。
最简单的消除电机高频方案是在电机和逆变器之间加装滤波器[7],电抗值越大,高频滤波效果越好,但电抗器上的电抗压降越大,从逆变器出来的电压越大,进而对逆变器的容量要求增加。对于电抗器带来的问题,有学者提出采用电感、电容及其组合装置的无源滤波方法[8]。该装置能够消除一定带宽的电流谐波,从而降低高频激振力和振动,但是这种电感电容需要的额定功率较大,因此器件的体积也较大。对于不同的工况需要不同的滤波电容或电感,FERREIRA J A等[9]提出一种可变滤波频率的结构,通过切换电容值可以在两个极限频率之间进行调整。针对无源滤波器的问题,许多学者提出有源滤波器的结构[10],逆变器与电机之间通过无源滤波器件相连,同时,另一套采用高开关频率MOSFET或者SiC器件的逆变器输出与主电路上无源滤波器中谐波反相位的谐波分量。该结构的缺点是两个逆变器需要时域上的协调控制才能达到良好的效果。
2)控制策略优化。
目前,国内外学者对低成本高频电磁振动噪声抑制研究主要集中在脉冲宽度调制(pulse width modulation,PWM)策略上,其思路为将载波频段附近的电压、电流、振动和噪声谐波分量分散到更宽的频带范围内。
文献[11-12]采用随机化载波频率,使原本集中的边带谐波能量扩展至较宽的频域范围,结果表明在中心频率的噪声抑制效果达到22 dB。为使采样频率固定,文献[13]提出一种变延时技术的随机开关频率脉宽调制方法,实验表明该方法能有效地将电流频谱均匀分布在较宽的范围内且能有效降低开关频率的幅值。文献[14]提出一种伪随机高频方波信号的随机开关频率脉宽调制方法,结果表明中心频率的噪声至少降了10 dB。为避免应用随机PWM方法时宽频率范围内引起电机振动的问题,文献[15]提出一种特定谐波消除的随机开关频率脉宽调制方法,并进行了仿真和实验结果验证。为了降低双三相永磁电机的高频电磁振动噪声,MIYAMA Y等[16]提出一种载波移相的调制方法来消除逆变器中的开关频率谐波,该方法通过优化功率管的触发角来消除主导的谐波电流。
西班牙的RUIZ G A等[17]提出一种梯形波为调制波的PWM控制方案,该方案中的电流谐波量大大减小,且谐波幅值也有效降低,从而力的幅值也随之减小。LE B J等[18]从理论出发探究载波频率的影响,得出最优载波频率的选取应该避开电机的0阶和2阶固有频率。华中科技大学的袁飞雄等[19]提出通过调节PWM载波来调节输出电流的频率和相位,从而与电机开槽振动的0或2p阶频率可以形成相消干涉,并在一台开绕组永磁同步电机上进行试验,结果表明,该方法有效降低了电机高频振动。
周期开关频率调制技术可以有效抑制高频电磁振动噪声。HUANG Jin等[20]对锯齿波的周期开关频率调制技术进行了研究,结果表明,中心频率段的线电压幅值至少降低30%。随后,该学者将锯齿波周期开关频率调制技术与异步载波调制技术相结合[21],进一步降低了高频电压的幅值。文献[22]对锯齿波和正弦波两种典型周期开关频率调制方法进行理论分析和不同工况下的电流及声振实验验证,结果表明,周期扩频调制能够有效抑制电机电流谐波且开关频率段中心频带噪声优化20 dBA以上。
综上,对于学者提出的随机和周期开关频率PWM调制策略效果而言,均以开关频率及附近振动噪声幅值作为评判标准。虽然幅值可以作为一种评价指标,但是电机的振动噪声是一个广谱参数值,且人耳对噪声的敏感并不局限于某个频率的噪声值,因此,在技术方案的振动噪声性能评估上应增加其他评判手段。本文提出从振动噪声的时域、频域以及1/3倍频程3个方面全面评价减振技术方案性能,对常用的周期开关频率PWM(periodic-switching-frequency PWM,PPWM)调制策略和随机开关频率PWM(random-switching-frequency PWM,RPWM)调制策略下电机高频电磁振动特性进行分析。首先,对变频器供电下的电机电磁场和电磁力进行计算和分析。然后,对PPWM和RPWM的振动抑制原理进行简要介绍。最后,对一台7.5 kW的永磁同步电机的振动进行实际测量,分析2种抑制方案的减振规律,详细探究2种抑制方案的影响因素,并从时域、频率以及1/3倍频程全方位对比2种方案的减振效果。
1 电磁力模型
永磁同步电机定子铁心振动主要由定子内表面所受到的径向电磁力Fn引起,则铁心内表面所受电磁力可以表示为
(1)
式中:Bn为铁心内表面气隙磁场的法向分量;μ0为空气磁导率。不考虑铁心磁路磁阻的影响,可以将永磁同步电机气隙磁场表示为
Bn(θ,t)=fa(θ,t)λ(θ,t)。
(2)
式中:θ为空间机械角度;fa(θ,t)为气隙磁动势;λ(θ,t)为气隙磁导。对于定子开槽时的气隙磁导可以近似表示为
(3)
式中:λ0是磁导平均分量;λl是气隙l次磁导分量。
变频器供电时永磁电机中的磁动势可写为
(4)
式中:p为电机极对数;ω0为电机基波角频率;φ为各项磁动势对应相位;ν为定子磁动势空间谐波次数;μ为转子磁动势空间谐波次数;k为谐波电流的次数;kω0为对应的角频率。变频器引入磁动势后可分为几项:③式为定子基波电流和转子永磁体产生的基波磁动势;④式为定子基波电流产生的谐波磁动势;⑤式为转子永磁体产生的谐波磁动势;⑥式为定子谐波电流产生的基波磁动势;⑦式为定子谐波电流产生的谐波磁动势。当使用正弦电流供电时,电机内不存在k次谐波电流,⑥式和⑦式所表示的磁动势不存在。当电机为变频器供电时,变频器输出的电压谐波会在电机内产生相同频率的电流谐波。
变频器供电时电机电流谐波的频率可表示为
fk=kω0/(2π)=k1fs±k2f0。
(5)
式中:fs是变频器载波频率;f0是电机的基波频率;k1和k2是奇偶互异的正整数,三相电机中,k2不能取3的倍数,如fs±2f0、fs±4f0、2fs±f0、2fs±5f0等。
综合式(1)~式(4),可求得变频驱动永磁电机中电磁力的阶次和频率特征。由于高次谐波磁导相对于平均磁导而言幅值较小,且谐波磁动势相对于空间基波磁动势幅值较小,因此,忽略高次谐波磁动势和高次谐波磁导(l≥2)的影响,整理得到电磁激振力的阶数和频率特性如表1所示。由表可知,当电机为正弦电流供电时,低频振动的阶数与电机的极对数、定转子谐波次数和槽数有关,振动的频率为电流基波的偶数倍频率,其中以2f0为主。当电机电流中存在频率为kf0低次电流谐波时,低次电流谐波也会引起低频振动,振动频率为(k±1)f0,振动阶数为0阶或2p阶。在载波频率及其倍频附近,变频器引入的电流谐波引起0阶或2p阶的高频振动,电磁激振力的频率表示为

表1 变频器供电时电机径向电磁力的阶数和频率
fn=(k±1)f0=k3fs±k4f0。
(6)
式中k3、k4是奇偶性相同的正整数,如fs±f0、fs±3f0、2fs±2f0、2fs±4f0等。
2 变开关频率PWM技术原理
当控制器采用PWM技术时,高次谐波电流会产生高频电磁振动噪声。在不增加硬件成本基础上,采用变载波周期的方案来解决电流开关频率集中的问题。本节介绍常见的变开关频率PWM技术——PPWM和RPWM。
2.1 周期开关频率
PPWM是在原有固定开关频率上增加一个周期变化的分量,开关频率表达式为
fs=fs0+R(t)Δf。
(7)
式中:fs0是中心频率;R(t)是输出范围为[-1,1]的周期函数;Δf表示开关频率的带宽。在一个周期内,开关频率在[fs0-Δf,fs0+Δf]内变化。选择fs0=8 000 Hz、Δf=500 Hz,R(t)是近似三角波函数,在程序实现中,每次进入增强型脉宽调制模块(enhanced pulse width modulation,ePWM)中断,令fs增加或减少1 Hz,fs变化波形示意如图1所示,R(t)周期近似为T=4Δf/(fs0Δf0),其中Δf0表示每个中断频率变化大小,fs在变化范围内近似均匀分布。
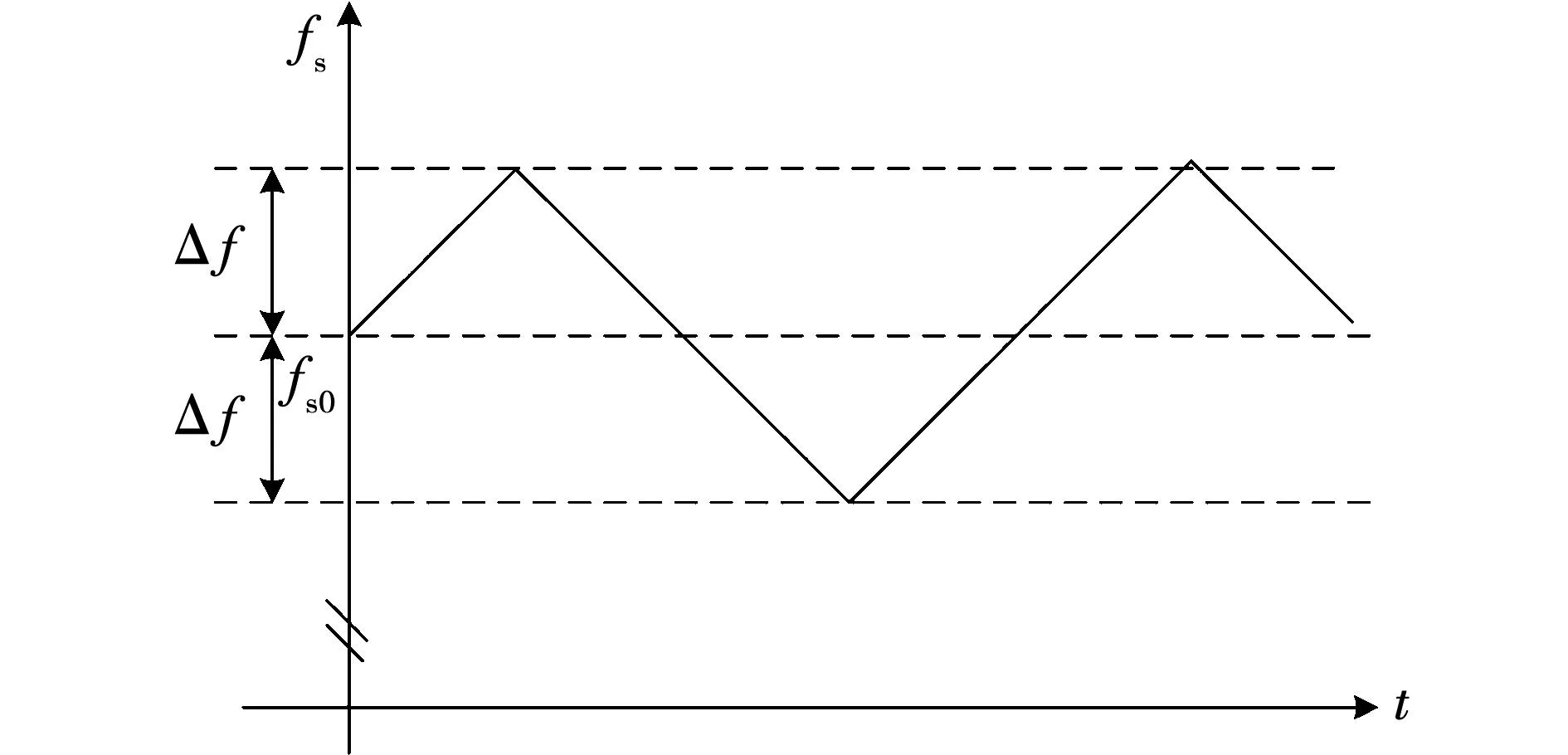
图1 周期载波频率波形示意图Fig.1 Waveform of periodic carrier frequency
2.2 随机开关频率
RPWM是目前最为常用的一种随机PWM方式,与周期开关频率相似,将随机开关频率表示为
fs=fs0+rand()Δf。
(8)
式中:fs0是中心频率;Δf是开关频率的变化范围;rand()是[-1,1]的随机函数,则fs是在[fs0-Δf,fs0+Δf]范围内随机变化的数值。具体实现方案为:在空间矢量脉宽调制程序执行过程中,随机改变电压矢量每次转过角度实现随机设置三角波信号斜率。
3 实验研究
为了探究2种变载波周期PWM技术对电机电磁振动的规律及影响,在一台8极表贴式永磁电机上进行详细的实验,实验平台如图2所示。实验装置包括:永磁电机、负载机、控制器、振动传感器以及江苏联能振动测试系统。

图2 实验装置Fig.2 Test rig
实验设置如下:为避免随机PWM技术方案对转速辨识的影响,采用编码器测量电机位置和转速,并反馈到转速环中。在固定开关频率控制方案的电机转速控制时,采用id=0的控制方式,转速稳定在1 500 r/min,负载为6 N·m,载波频率为8 kHz。在周期开关频率中,研究了频率变化步长为1、5、10和20这4种长度对振动的影响,并探究了频率带范围对PPWM和RPWM的减振效果影响。实验过程中,待电机运转平稳后,分别测量电机的相电流以及电机机壳表面的振动,截取的数据处理段为稳定的无波动的时域电流和振动信号,处理结果在下文进行总结。
3.1 固定开关频率
图3和图4分别为电机在1 500 r/min,负载6 N·m工况下的电流和振动波形。通过固定载波频率控制方案下的相电流和径向振动加速度及傅里叶分解结果可知,电流的高频谐波分量集中在开关频率fs及其整数倍附近,其频率分布与理论推导式(5)及文献[2-10]中的结论一致,而这些高频谐波分量是由逆变器输出的电压高频谐波分量引起的。由图4可知,径向电磁振动中的高频分量幅值主要集中在开关频率fs及其整数倍附近,其频率分布与理论推导式(6)及文献[2-10]中结论一致。
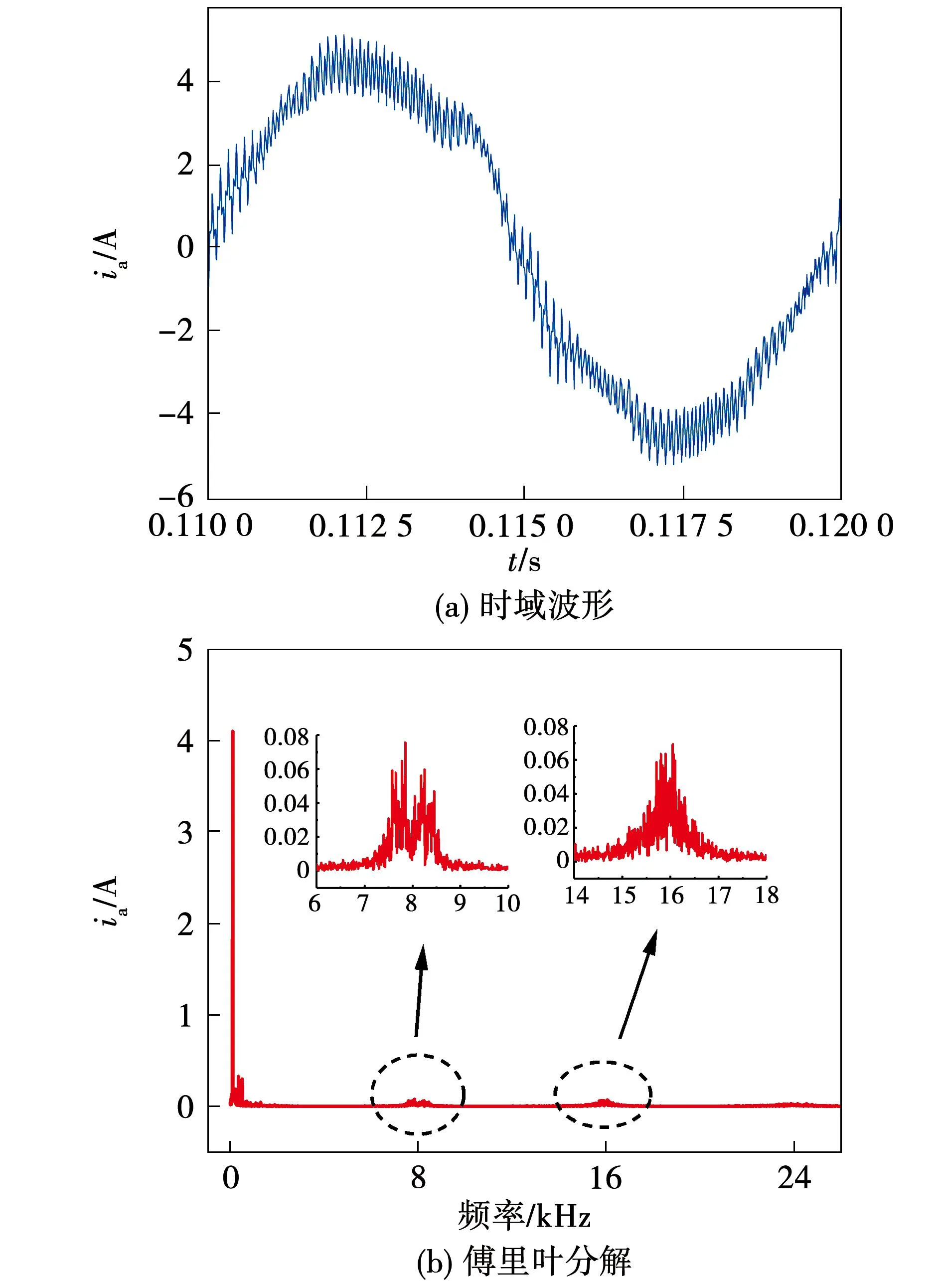
图3 电机在1 500 r/min,转矩6 N·m时的电流波形Fig.3 Motor current at 1 500 r/min under T=6 N·m

图4 电机在1 500 r/min,转矩6 N·m时的振动波形Fig.4 Motor vibration at 1 500 r/min under T=6 N·m
3.2 周期变开关频率PWM技术
图5和图6分别为采用PPWM技术时电机运行在转速1 500 r/min,负载6 N·m工况下的电流和振动波形。由图5(a)的时域波形可知,此时的电流发生了畸变,并存在一些低次谐波。由图5(b)频域波形可知,当采用PPWM技术时,开关频率及其整数倍附近窄带宽的高频谐波电流的幅值将被有效削弱,能量分散到其他频率分量中,并向低频方向进行分散。由此可知,若范围宽度进一步增大,将使高频谐波能量向更低频方向移动,造成控制不稳定。从幅值来看,高频谐波电流分量幅值在开关频率fs附近削弱了64.7%,在2倍开关频率2fs及3倍开关频率3fs附近都削弱了70%以上。由图6可知,采用周期开关频率PWM技术后,1倍、2倍和3倍开关频率附近的振动分量幅值分别为1.7、8.2和3.1 m/s2,与固定开关频率技术方案相比,其削弱比例分别为76.3%、68%和86%。从时域波形来看,其振幅最大值为98.2 m/s2,大于固定开关频率时的振动幅值75.1 m/s2。

图5 电机在1 500 r/min,转矩6 N·m时的电流波形Fig.5 Motor current at 1 500 r/min under T=6 N·m
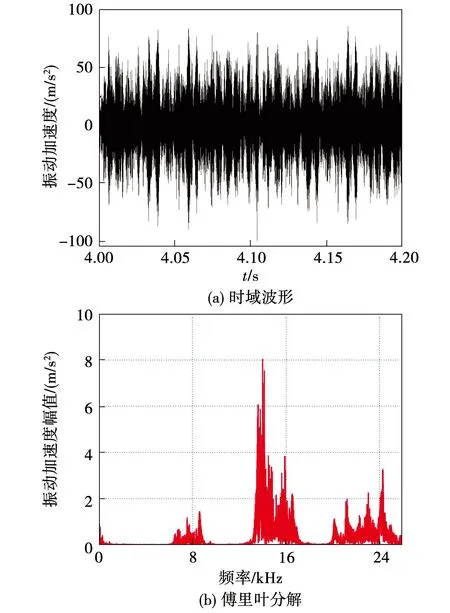
图6 电机在1 500 r/min,转矩6 N·m时的振动波形Fig.6 Motor vibration at 1 500 r/min under T=6 N·m
从噪声表现上来看,由于开关频率振动的幅值被有效削减,人耳感知不到固定开关频率引起的高频啸叫声,但这些分散的频率分量将引起电机的沙沙声,该声音是固有开关频率控制方案所没有的,从噪声来看,采用周期PWM控制方案引起的沙沙声也会降低电机的噪声、振动和声振粗糙度品质。
3.3 随机PWM技术
图7为采用RPWM技术时电机运行在1 500 r/min,负载6 N·m工况下的电流波形。与图3相比,电流发生了畸变,同时存在一些低次谐波。由图7(b)的频域波形可知,该方法能有效抑制开关频率及其整数倍附近的高频谐波电流的幅值,但能量分散到频率带宽中。从幅值来看,高频谐波电流分量幅值在开关频率fs附近削弱了54%,在2倍开关频率2fs及3倍开关频率3fs附近都削弱了60%以上。
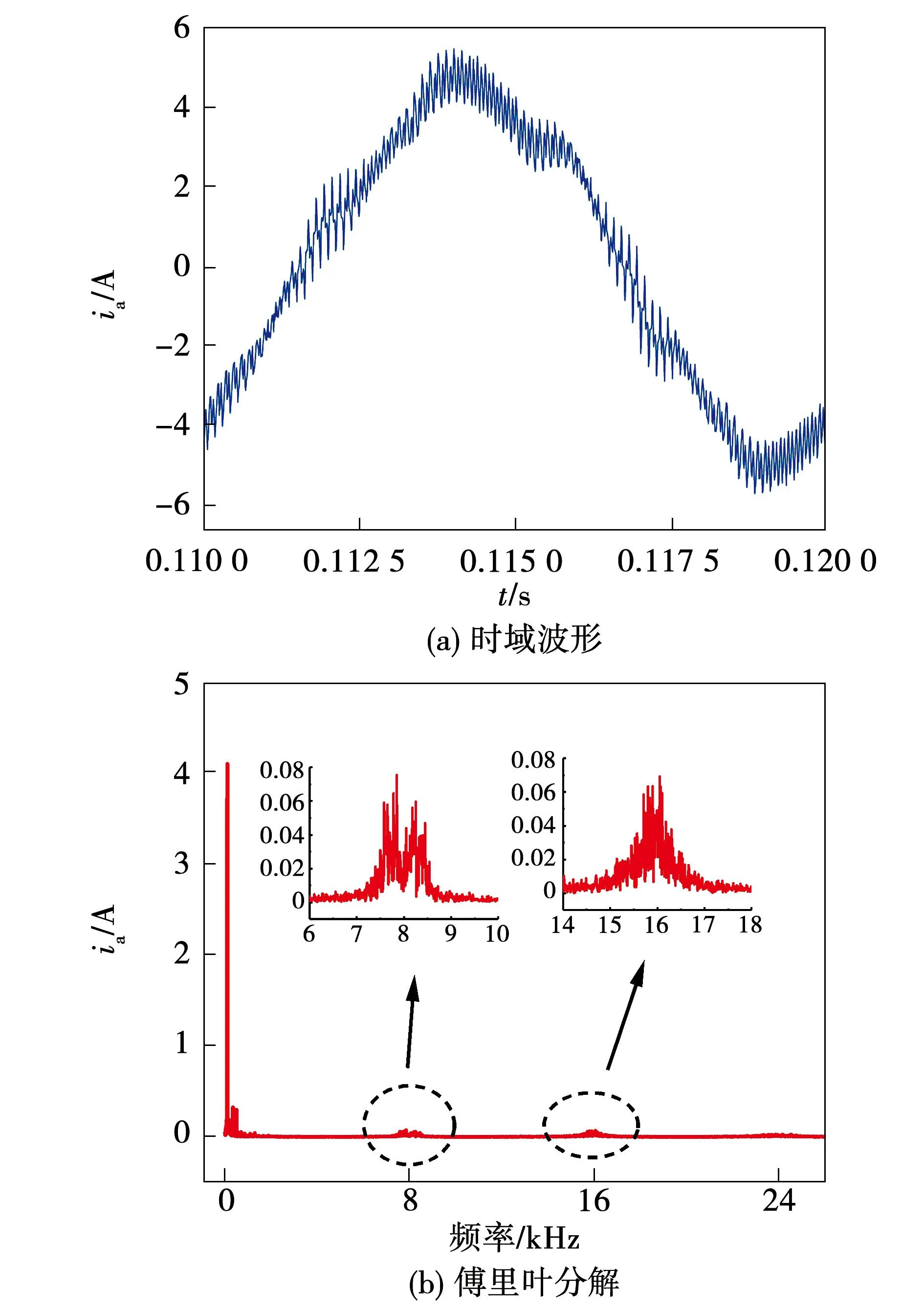
图7 电机在1 500 r/min,转矩6 N·m时的电流波形Fig.7 Motor current at 1 500 r/min under T=6 N·m
图8为该工况下的振动加速度结果。由图可知,1倍、2倍和3倍开关频率附近的振动分量幅值分别为3.0、6.9和6.8 m/s2,与固定开关频率技术方案相比,其削弱比例分别为45.4%、72.4%和72.9%。从时域波形来看,其振幅最大值为103.2 m/s2,大于固定开关频率时的振动幅值。从噪音来看,该控制方案下电机噪声规律与周期开关频率控制下电机的噪声规律类似,电机将出现沙沙声。
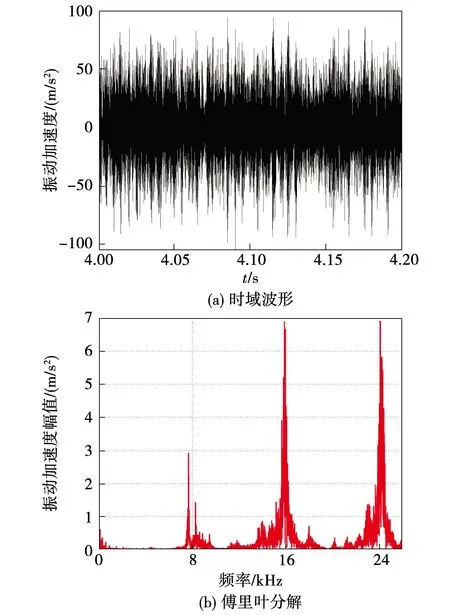
图8 电机在1 500 r/min,转矩6 N·m时的振动波形Fig.8 Motor vibration at 1 500 r/min under T=6 N·m
3.4 方案对比
本文3.2节和3.3节从频域角度对方案的减振规律和效果进行了描述,尤其是开关频率附近的振动幅值指标,该指标也是目前研究人员普遍采用的评价方式。然而,采用变开关频率PWM控制方案将会引起额外的振动频率,这些频率会增加电机的沙沙声。此外,由图4(a)、图6(a)和图8(a)可知,采用PPWM和RPWM技术方案时电机的电磁振动幅值大于固定开关频率方案时的电磁振动,因此,为了全方位客观评价技术方案的振动噪声指标以及性能,本节将从时域和频域的均方根值以及A记权的1/3倍频程振动加速度级进行评价。
为了更好地评价2种方案的效果,采用均方根值对电机电磁振动信号能量进行求解,其表达式为
(9)
式中:ai为第i个时域点或频率点的振动加速度;N为计算的个数;aRMS为N点内的加速度均方根值。
利用式(9)计算一个电周期内振动加速度时域信号的均方根值,然后,对振动加速度时域信号进行傅里叶分解得到振动加速度的频域值,取不同区间该频率段内振动加速度值进行均方根值求解,计算的时域和频域均方根值结果见表2。由表可知,从时域均方根值来看,PPWM和RPWM技术方案下的振动信号均方根值分别为30.97和29.34,均大于固定开关频率控制下的振动信号均方根值27.12。从频域均方根值下的振动能量信号值来看,6 k~10 k频段内,RPWM技术方案下的振动信号均方根值为5.9,大于固定开关频率控制下的振动信号均方根值5.43。12 k~18 k频段内,PPWM技术方案下的振动信号均方根值为23.4,大于固定开关频率控制下的振动信号均方根值15.6。而在20 k~26 k频段内,变开关频率PWM技术方案下的振动信号能量均大于固定开关频率控制下的振动信号能量。
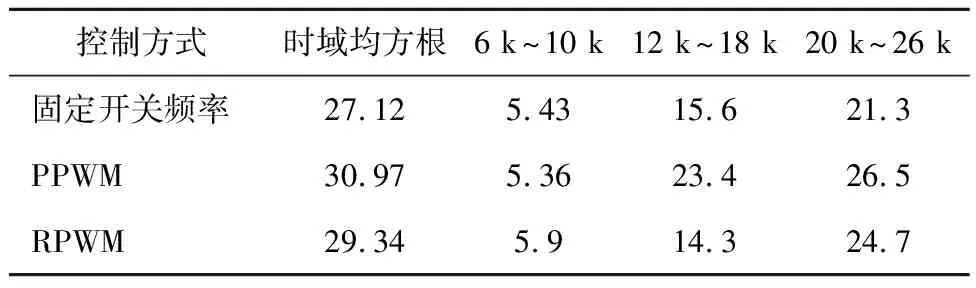
表2 不同PWM调制方案下能量值对比
常用的一种振动评价方案为振动加速度级对比,《环境振动标准》[23]定义振动加速度级为
(10)
式中:a为振动加速度有效值;a0为基准加速度有效值,取a0=10-6m/s2,振动加速度级单位为分贝(dB)。1/3倍频程谱是一种常见的表征振动与噪声的方式,目的是将一定带宽内信号能量用一条谱线表示,具有频带宽谱线少,易于人耳敏感度区分的特点。每个频带成为一个频程,频带的划分采用恒定带宽比。1/3倍频程对高频区分度低,对低频区分度高,符合人耳对不同频率声音的敏感程度。总振级VL是在所有频带内的总振动加速度级,可以根据不同频带内振动加速度级计算得出,即
(11)
图9为负载6 N·m时3种不同开关频率PWM控制方式不同转速下电机总振动加速度级,由图可知,不论是300、900还是1 500 r/min,变开关频率PWM控制方案下的电机振动加速度级均大于固定开关频率PWM控制方案下的振动加速度级。周期开关频率的振动加速度级最大,随机开关频率次之,固定开关频率最小。以1 500 r/min为例,固定、周期和随机开关频率控制方案下电机振动加速度级分别为146.5、146.8和151.6 dB。
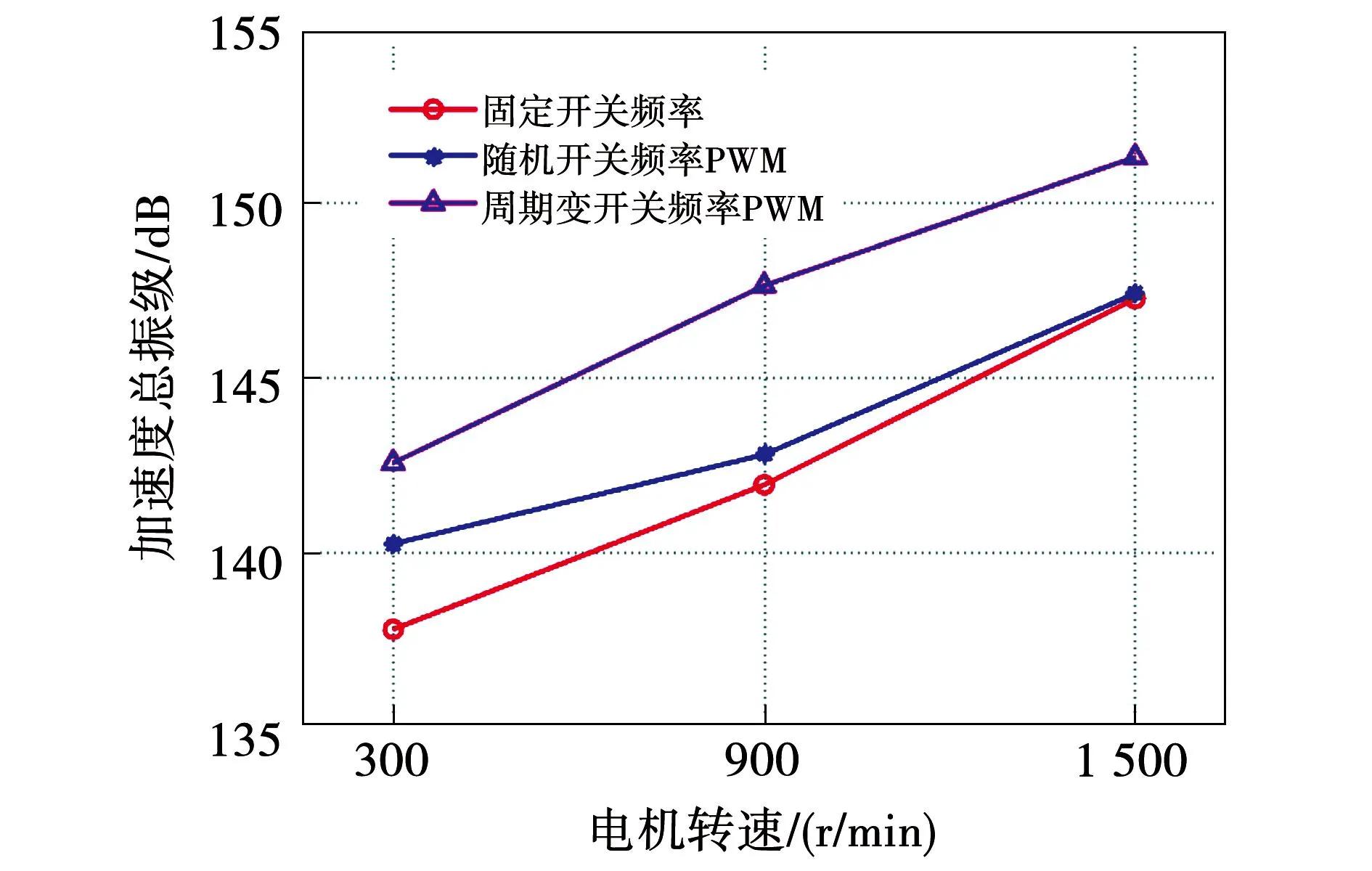
图9 负载6 N·m时不同控制方式不同转速下电机总振动级Fig.9 Motor VL in different control type and speed under T=6 N·m
图10为PPWM技术方案不同变化步长时的电机总振动级。该方案中,电机施加的负载转矩为1 N·m。由图可知,PPWM技术方案下的电机总振级大于固定开关频率PWM技术方案下的总振级,随着步长step的增加,电机的总振级逐渐减小。事实上,随着步长step的增加,电机电流的控制难度也增加。
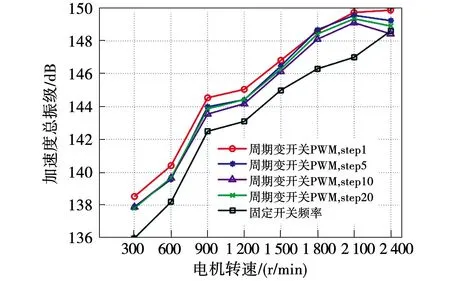
图10 周期PWM技术方案不同步长时的振动加速度级Fig.10 Motor VL in different step in PPWM
图11和图12分别为不同开关频率范围时不同转速周期开关频率PWM技术和随机开关频率PWM技术方案下的电机总振级。由图可知,当开关频率范围增加时,PPWM技术方案时电机的总振级在减小,而RPWM技术方案时电机的总振级幅值略微增加,但变化幅度不大。不论选择多宽的开关频率范围均会增加电机的总振级。此外,过大的开关频率范围会影响电机的控制性能。
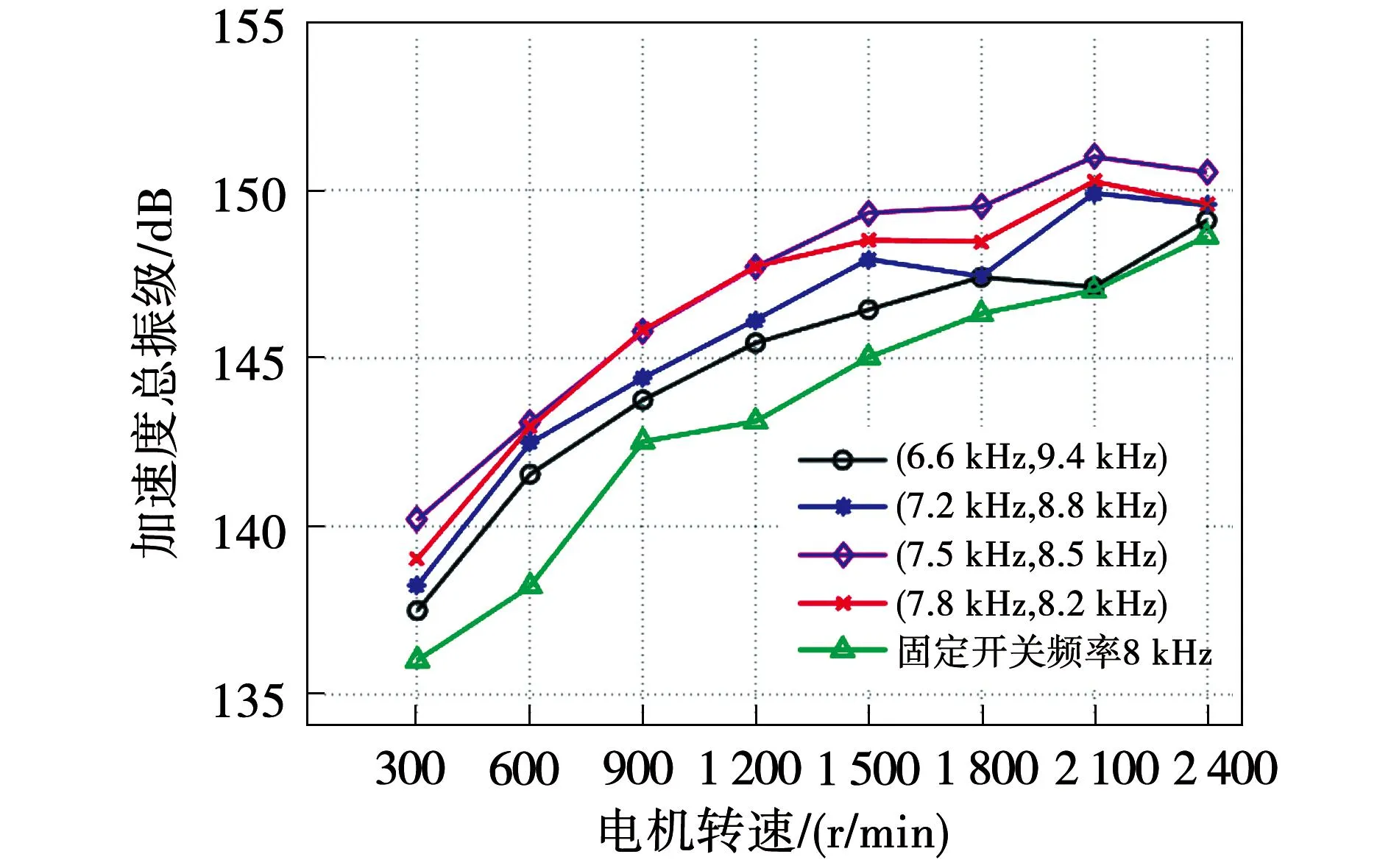
图11 周期开关频率PWM技术方案时不同开关频率范围的电机总振级Fig.11 Motor VL in different frequency band in PPWM
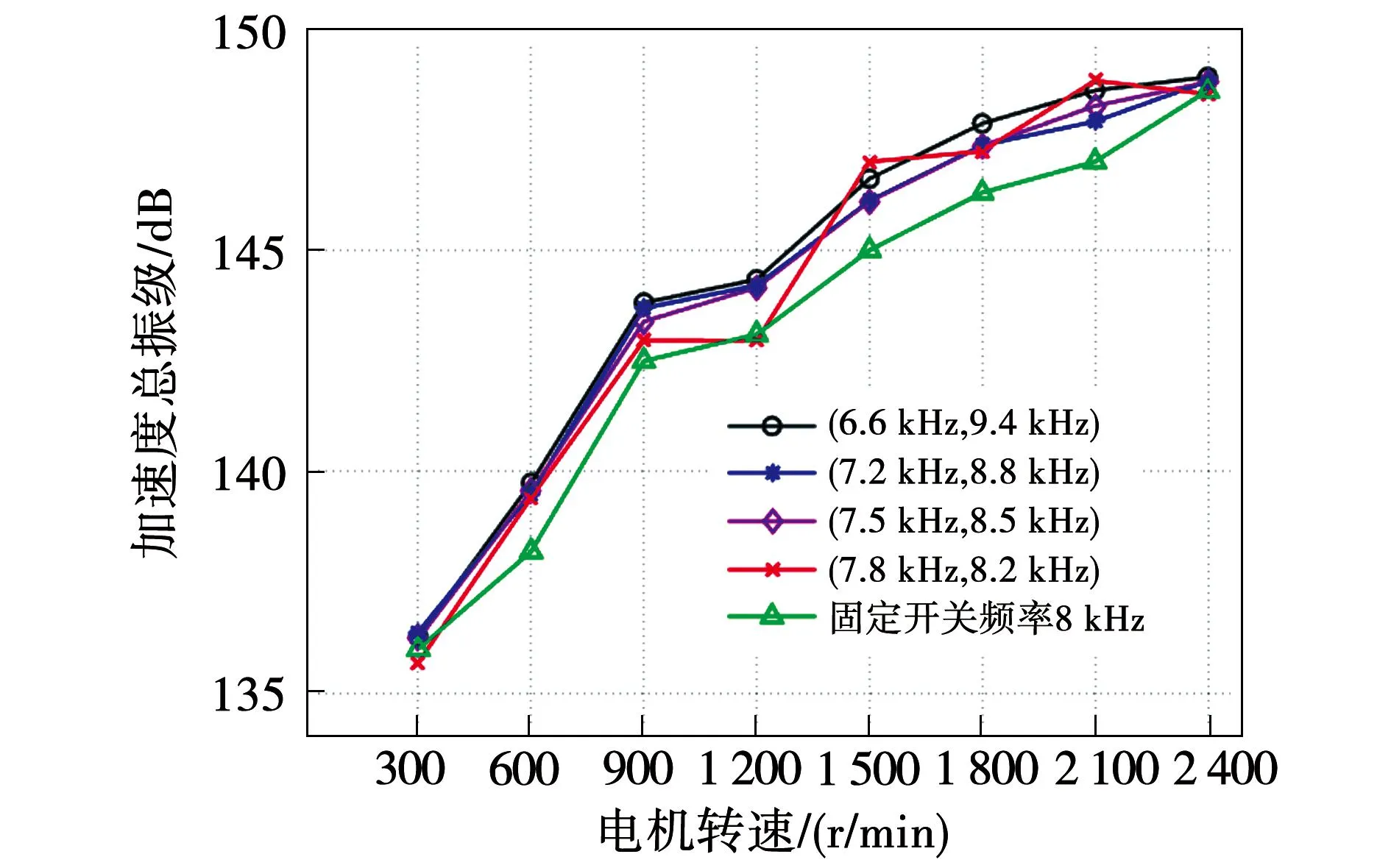
图12 随机PWM控制下不同开关频率范围电机总振级Fig.12 Motor VL in different frequency band in RPWM
4 结 论
本文主要探究了在PPWM控制方案和RPWM控制方案下,从电机振动的时域、频域以及1/3倍频程方面分析高频电磁振动的特性规律,得出以下结论。
1)变频器引入后,电机电流中除幅值较大的基波和低次谐波分量外,还存在一些高频谐波分量。低次谐波电流会引起电机的低频振动噪声,而高频电流谐波主要集中在开关频率fs及其整数倍附近,这些高频谐波电流会产生较大幅值的振动噪声。
2)PPWM 技术能有效削弱开关频率及其整数倍附近电磁振动的谐波分量峰值,但并不能降低电机的总振动加速度级。振动加速度级受到周期步长和开关频率范围的影响。步长越大,总振动加速度级越小;开关频率范围越大,总振动加速度级越小。
3)RPWM 技术可以极大削弱开关频率及其整数倍附近电磁振动的高频谐波幅值,但并不能降低电机的总振动加速度级。振动加速度级受到随机频率宽度的影响。宽度越小,总振动加速度级越小。
4)PPWM和RPWM技术的引入会增加电机的沙沙声,从时域均方根值以及1/3倍频程能量谱的评价来看,2种技术方案下电机电磁振动能量并无降低,减振效果有限。
