非晶合金轴向永磁电机永磁体涡流损耗抑制措施研究

韩雪岩, 王佳兴, 朱龙飞

(沈阳工业大学 国家稀土永磁电机工程技术中心,辽宁 沈阳 110870)

0 引 言

轴向电机具有独特的扁平结构,其轴向长度短、功率密度高、转动惯量小、结构紧密,在对电机结构、体积要求较高的领域有着广阔的应用前景[1-2]。非晶合金的高电阻率与超薄特性使得其铁耗极低,将其作为轴向电机的定子铁心可有效降低高频工况下的定子铁耗[3]。但在高频应用场景下,尤其是定子开槽以及分数槽集中绕组的应用,使得定子电流谐波、绕组磁动势谐波、气隙磁导谐波在永磁体中引起涡流损耗,导致永磁体温升过高,存在不可逆失磁的风险[4-5],非晶合金轴向电机永磁体涡流损耗的抑制对于电机的平稳运行具有重要意义。

目前针对径向磁路电机永磁体涡流损耗抑制措施已得到广泛研究。文献[6-7]通过永磁体分块的方式抑制涡流损耗,对比径向与周向不同分块数量下的损耗抑制情况。文献[8-9]对电机采用不同材料与不同结构槽楔下的转子损耗进行计算,得出磁性槽楔可有效抑制永磁体涡流损耗,槽楔材料与结构不同,对涡流损耗的抑制效果差别较大。以上研究均针对传统径向电机,针对非晶合金轴向电机永磁体涡流损耗的抑制研究仍不够全面,与径向电机不同的是,非晶合金轴向电机拓扑结构特殊、散热条件差、对永磁体涡流损耗抑制要求更高,以上因素决定了需对其涡流损耗抑制措施进行进一步研究。

本文以1台7 kW非晶合金轴向磁通永磁同步电机为样机,给出电机参数,建立样机的三维有限元模型并通过实验对仿真结果加以验证。通过磁场计算分析,分别得出永磁体分块、磁性槽楔对非晶合金轴向电机永磁体涡流损耗抑制效果,通过对永磁体不完全分块来降低工艺难度,确定磁性槽楔相对磁导率最佳范围。

1 样机结构参数与仿真实验

1.1 样机结构参数

本文研究的7 kW双定子单转子非晶合金轴向电机额定参数与主要尺寸如表1所示。其中电机定子由非晶合金卷绕成盘后加工开槽,背面加工水平与端盖采用粘结工艺,不需加工燕尾槽,转子采用无铁心结构,采用不锈钢材料作为转子支架。定子结构及磁化特性曲线如图1所示。

1.2 三维仿真模型

采用A,φ-A法的三维有限元计算永磁体涡流损耗时,其涡流区控制方程[10]为:

(1)

(2)

(3)

式中:A、φ分别为矢量磁位与标量电位;Ja为电枢电流密度;μ为磁导率;σ为电导率;M为永磁体磁化强度;νa和ia分别为电枢电压和电流;Ra为电枢绕组电阻;Φ为电枢绕组磁链。得到A与φ后,可通过下式计算永磁体内涡流损耗:

(4)

式中T为计算时间。

图2为建立的样机三维有限元模型,为了提高计算效率,选择电机的1/12进行计算。转子支架为不锈钢材质,其中支架内部凹槽与永磁体凸起部分相扣实现了永磁体的固定,支架上下两部分通过固定孔处螺栓实现了最终夹紧。

图2 非晶合金轴向电机1/12模型Fig.2 Amorphous alloy axial motor 1/12 mode

1.3 实验验证

为了验证本文三维有限元计算永磁体涡流损耗仿真结果的正确性,对7 kW样机在500 Hz运转状态下进行空载正弦波供电及空载PWM供电试验,试验如图3所示。

图3 非晶合金轴向电机空载实验平台Fig.3 Amorphous alloy axial motor no-load experimental platform

其中正弦波供电电源由直流电动机拖动三相高频永磁发电机产生,通过调节直流电机转速进而调节样机供电电压频率,通过调节调压器来改变被测电机供电电压大小,最终测得空载PWM供电与正弦波供电下电机输入功率分别为421.9、266.59 W。

由于试验中很难分离铁心损耗与永磁体损耗,并且空载情况下电机的铜耗很小,因此在忽略PWM谐波对电机铜耗影响的前提下,空载PWM供电下电机输入功率与空载正弦供电下电机输入功率之差,即为实验得出的由PWM谐波引起的电机永磁体与铁心损耗之和。最终三维仿真结果及试验数据对比如表2所示。

表2 由空载PWM电流谐波引起的铁耗和永磁体涡流损耗仿真值与实验值对比

由表2可知,由于有限元计算损耗过程中处于理想状态下,计算受剖分精度,计算步长等因素影响,仿真结果略低于实验结果。本文将三维仿真下永磁体与铁心损耗总和与实验值误差控制在20%以内,使得文中的三维有限元损耗模型具有一定精度,可为后续研究提供依据。

2 永磁体分块型式不同对涡流损耗的影响

通过将一整块永磁体分割成多个小块,各小块之间相互绝缘,进而阻断了涡流原有路径,从而达到降低永磁体涡流损耗的目的。

2.1 永磁体完全分块

永磁体分块方向主要为径向与周向以及径向与周向的组合方式,不同的分块方向对涡流路径的阻断效果不同,为了使损耗变化趋势更具代表性,本文最多计算了分8块下的永磁体损耗情况。

图4为PWM供电下扇形永磁体未分块时的涡流路径及损耗分布,图5、图6分别为永磁体不同方向分2～8块下的损耗分布情况。

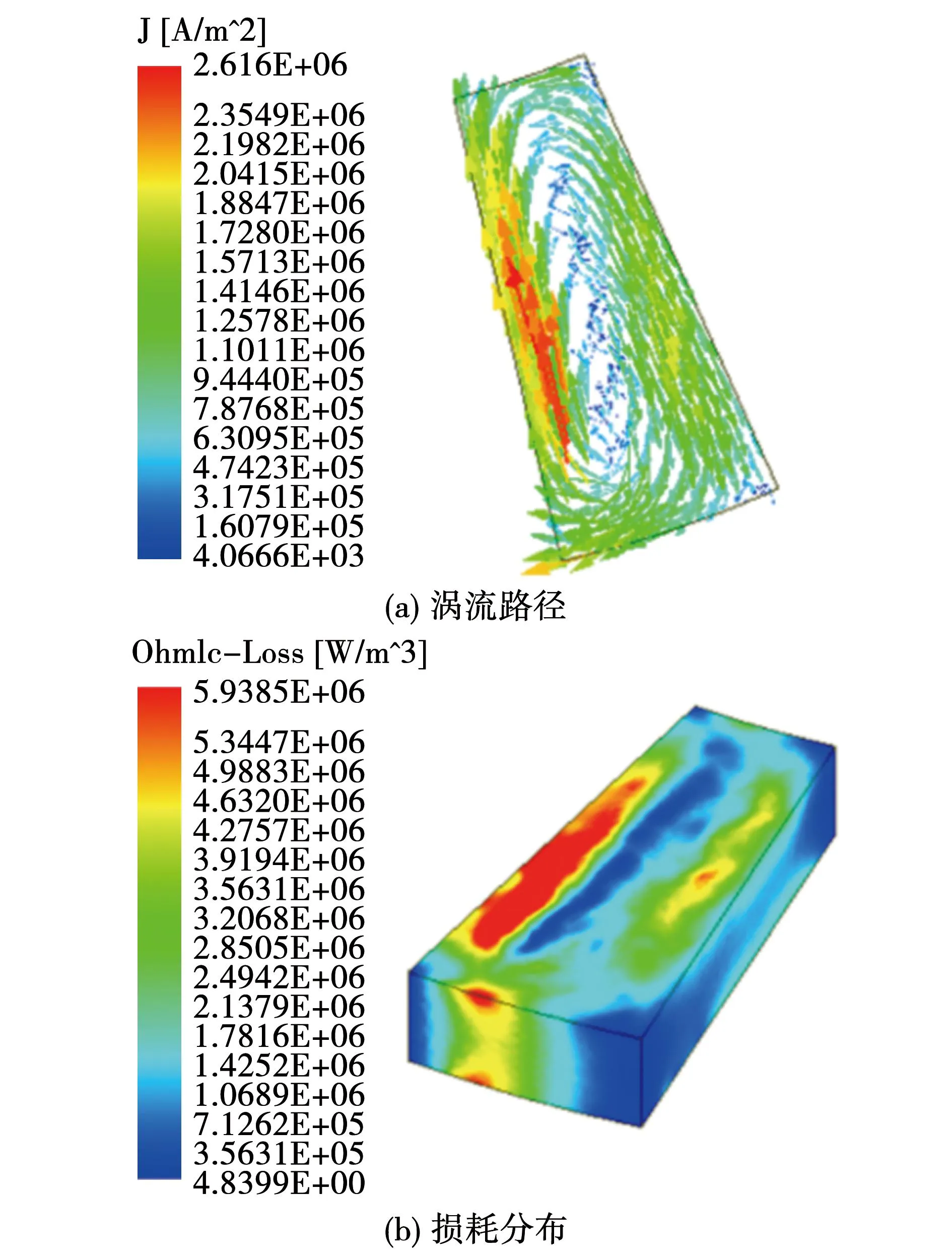
图4 永磁体未分块时涡流分布Fig.4 Eddy current distribution when the permanent magnet is not divided into blocks

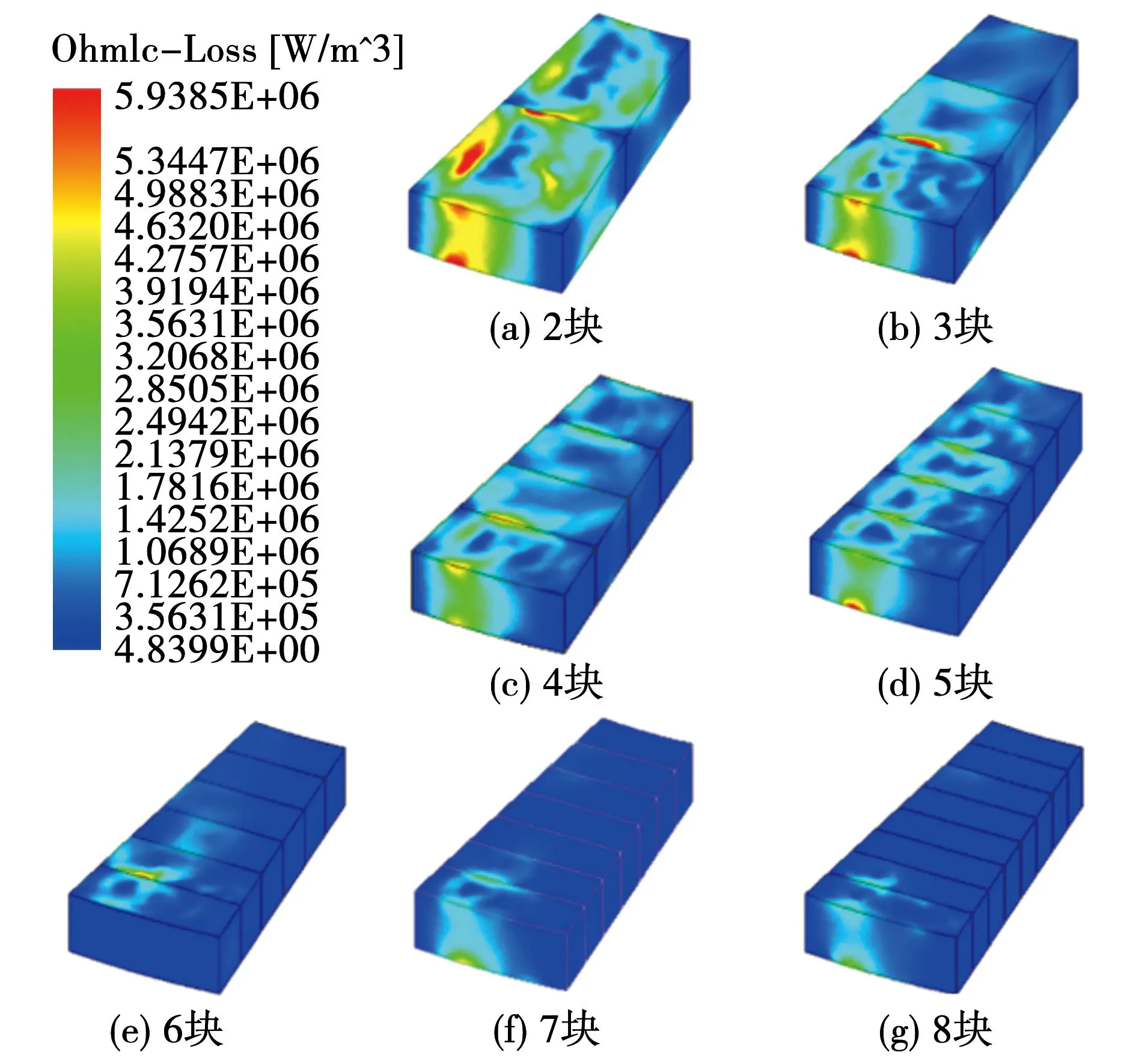
图5 永磁体径向不同分块数下损耗分布Fig.5 Loss distribution of permanent magnets with different numbers of radial segments

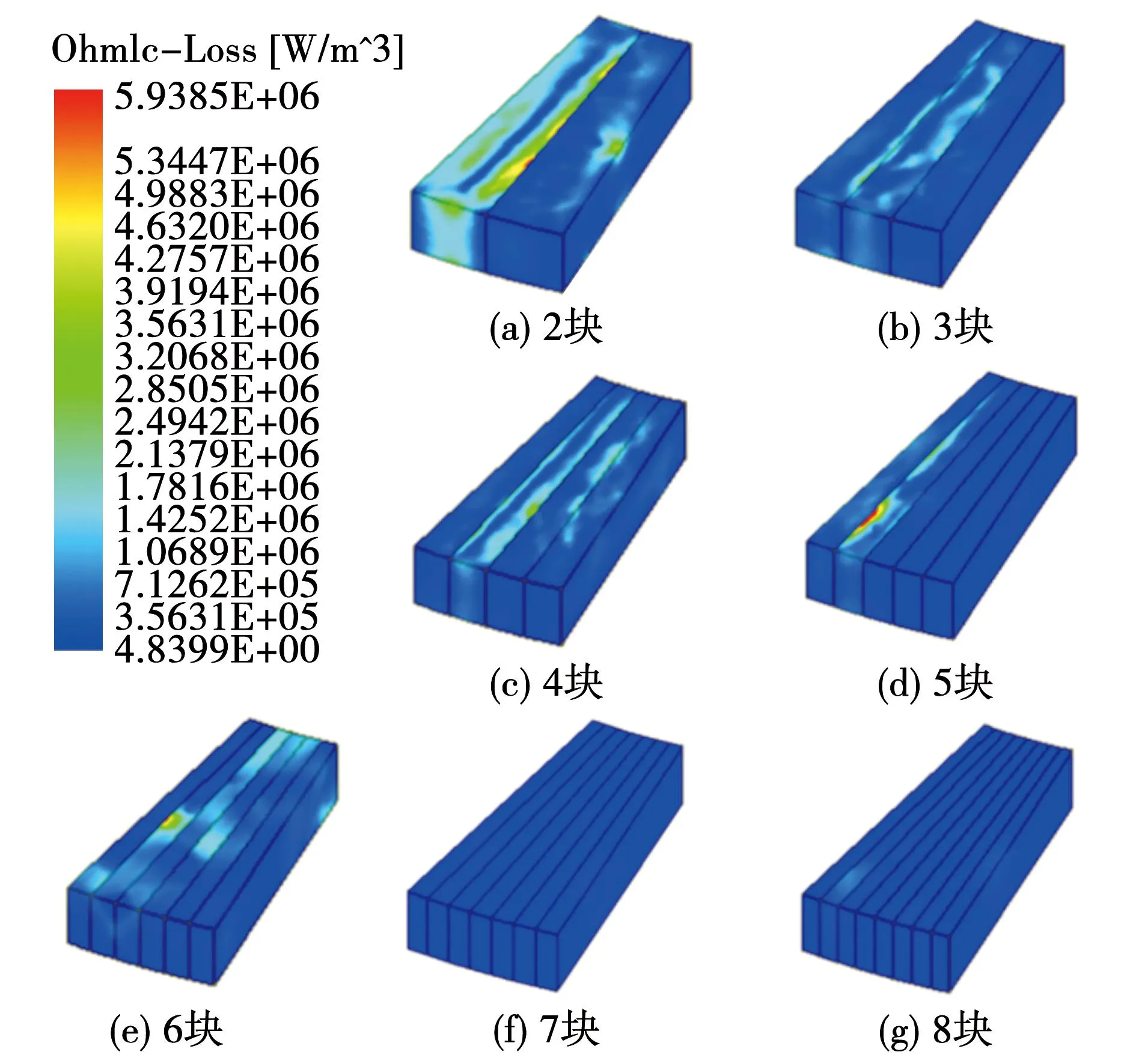
图6 永磁体周向不同分块数下损耗分布Fig.6 Loss distribution of permanent magnets with different number of blocks in the circumferential direction

由图4可知,涡流在永磁体上贴近外圈以环形运动,相应的损耗分布呈现边缘高、中间低、四角最低的特点。

由图5、图6可知,永磁体分块后对其损耗产生了抑制作用,但不同分块方向对损耗的抑制效果不同。径向分6～8块后永磁体无较高损耗分布,而周向分3块后损耗分布已有明显变化。

不同分块方向及分块数下永磁体涡流损耗计算结果如图7所示。

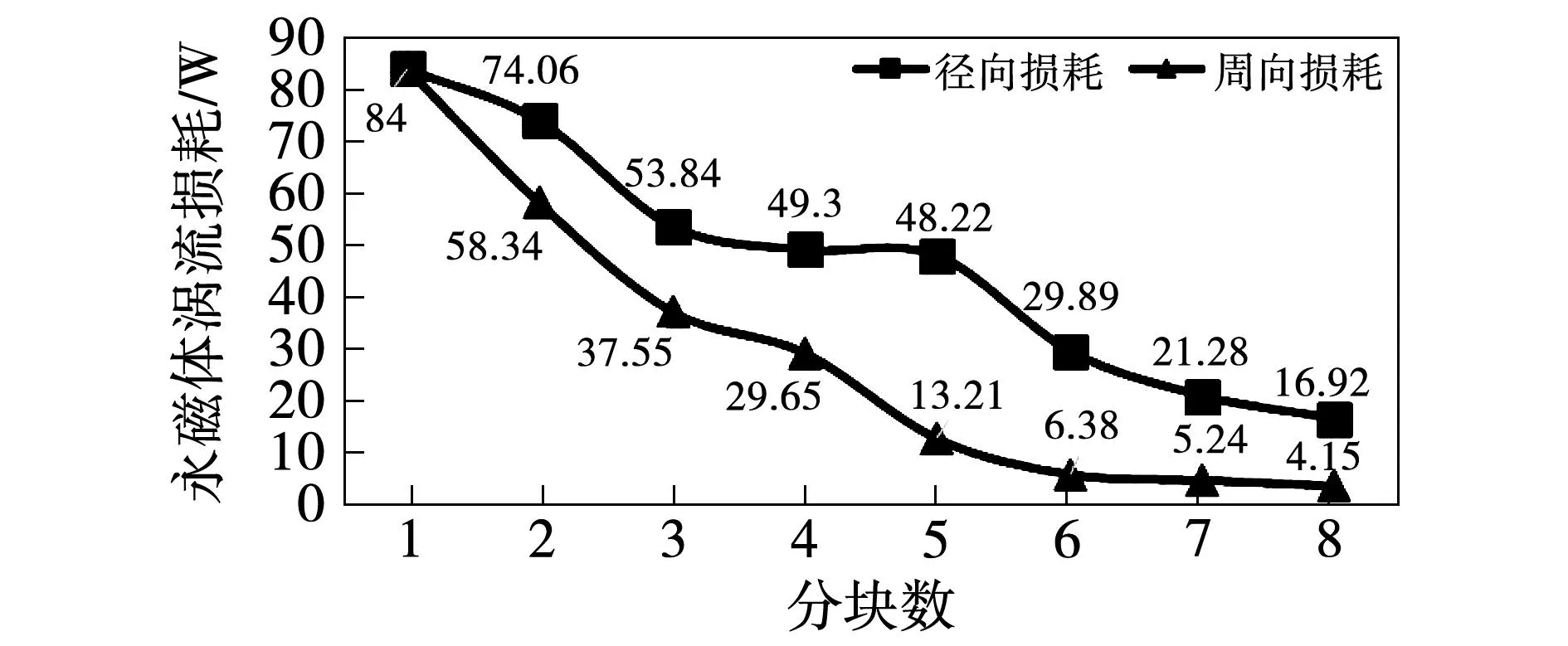
图7 不同方向及分块数下永磁体涡流损耗计算结果Fig.7 Results of permanent magnet eddy current loss in different directions and number of blocks

由图7可知,损耗随分块变化趋势非线性变化,同一分块数下,周向分块的损耗抑制作用整体优于径向,主要原因为周向分块将永磁体分为狭长的小块,产生的绝缘长度远大于径向分块,从而更有利于涡流的阻断。

不同分块数下涡流损耗变化率也不同,如径向分4块和5块时,损耗仅下降2.19%,其变化率过低主要是由于永磁体上的涡流路径受各小块长宽比影响。由于分块方向不同,周向分块每增加分块数,其小永磁块长宽比急剧增加,小永磁块变得更为狭长,对涡流的抑制作用较高。而由图5可知,径向分块数量的增加并不一定能提高小永磁块的长宽比,其长宽比非线性变化,因此也造成径向分4块和5块时,损耗的抑制提升不明显。

因此,为了进一步探究永磁体涡流损耗随分块数的变化规律,图8计算了不同分块数下的涡流损耗相对变化率,计算结果可表征分块数增加对损耗的影响程度,进而为分块数量的选择提供依据。

图8 不同分块方式及分块数下涡流损耗相对下降率Fig.8 Relative decline rate of eddy current loss under different block methods and block numbers

由图8可知,两种分块方式涡流损耗相对变化率均随分块数的增加呈现上升-下降-上升-下降的变化规律。

周向分3块、5块、6块时损耗下降率较大,其中分3块时实现了涡流损耗的部分抑制,同时由于分块数较少,工艺上更好实现,但对损耗的抑制不彻底。分5块和6块时已实现大部分涡流损耗的抑制,相比于未进行分块时,涡流损耗分别下降了84.27%、92.40%,但由于分块数较多,增加了工艺难度。

径向分3块、6块时损耗下降率较高,但下降率低于周向分块,可选择的分块方案较少,同时对损耗的抑制效果也低于周向分块。

除单方向分块外,本文进一步对比了径向与周向组合分块对永磁体涡流损耗的抑制作用,组合式分块的特点为,其仅有分4/6/8等偶数块的可能,且6块与8块又各分为两种形式。组合分块下永磁体涡流损耗分布如图9所示,不同分块方式下永磁体涡流损耗对比如表3所示。

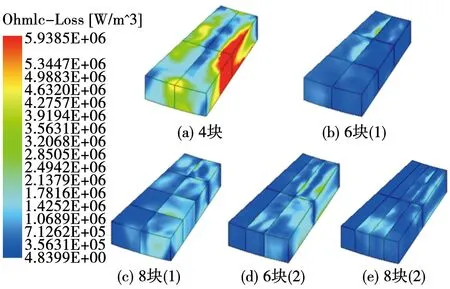
图9 永磁体组合分块下损耗分布Fig.9 Loss distribution under the combined block of permanent magnets

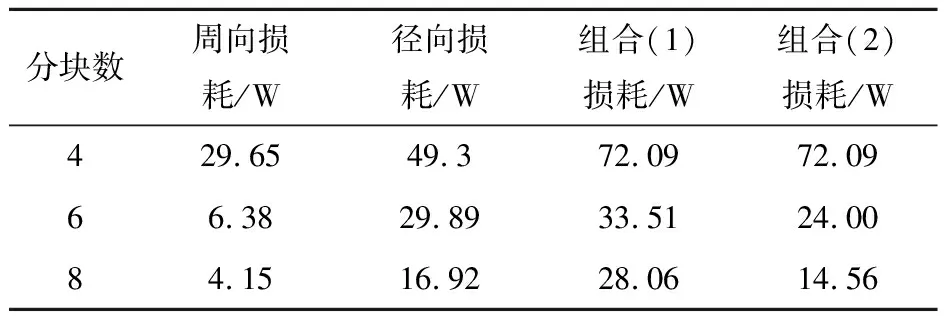
表3 3种分块方式下永磁体涡流损耗对比

由图9可知,在组合分块方式中,分块数相同而分块形式不同,也会影响损耗的分布。图中分块形式(2)由于在同等分块数下将永磁体分为更狭长,即长宽比更大的小块,对永磁体涡流损耗的抑制作用明显增强,而形式(1)中的永磁体小块长宽比更接近于1,对涡流的抑制作用明显低于形式(2)。

由表3可知,在分块数为4时,组合分块对永磁体损耗的抑制能力最差,当分块数高于4时,组合形式(1)的损耗抑制能力最差,组合形式(2)的抑制能力要强于径向分块,而无论分块数为几,周向分块对损耗的抑制能力一直最高。因此,综合上述对比,针对本样机扇形永磁体,周向分块方式对损耗的抑制能力要高于其他3种分块形式,能以较少的分块数实现最多的损耗抑制。

2.2 永磁体不完全分块

由以上分析可知,当永磁体周向完全分多块时,可以对永磁体涡流损耗实现大部分抑制,但对永磁体完全分块在永磁体加工、粘合、装配过程中会产生一系列工艺问题,加大了工艺难度。

本文进一步探究了永磁体周向不完全分块即单面开缝隙抑制涡流损耗,由于上文永磁体完全分块中,已得出周向分5块即可抑制永磁体大部分损耗,因此本节首先对永磁体周向分5块下,对比了开缝隙深度分别为1、3、5、7 mm下永磁体涡流损耗的变化,在确定最佳缝隙深度后,下文进一步研究了缝隙深度不变,不完全分块数量对永磁体涡流损耗的抑制作用。为了消除永磁体因体积减少造成的损耗误差,开缝宽度应尽可能小,本次选为0.5 mm,不同开缝深度下永磁体三维模型如图10所示。

图10 不同缝隙深度下永磁体三维模型Fig.10 3D models of PM with different gap depths

通过三维有限元对不同缝隙深度下永磁体涡流损耗计算结果如图11所示。

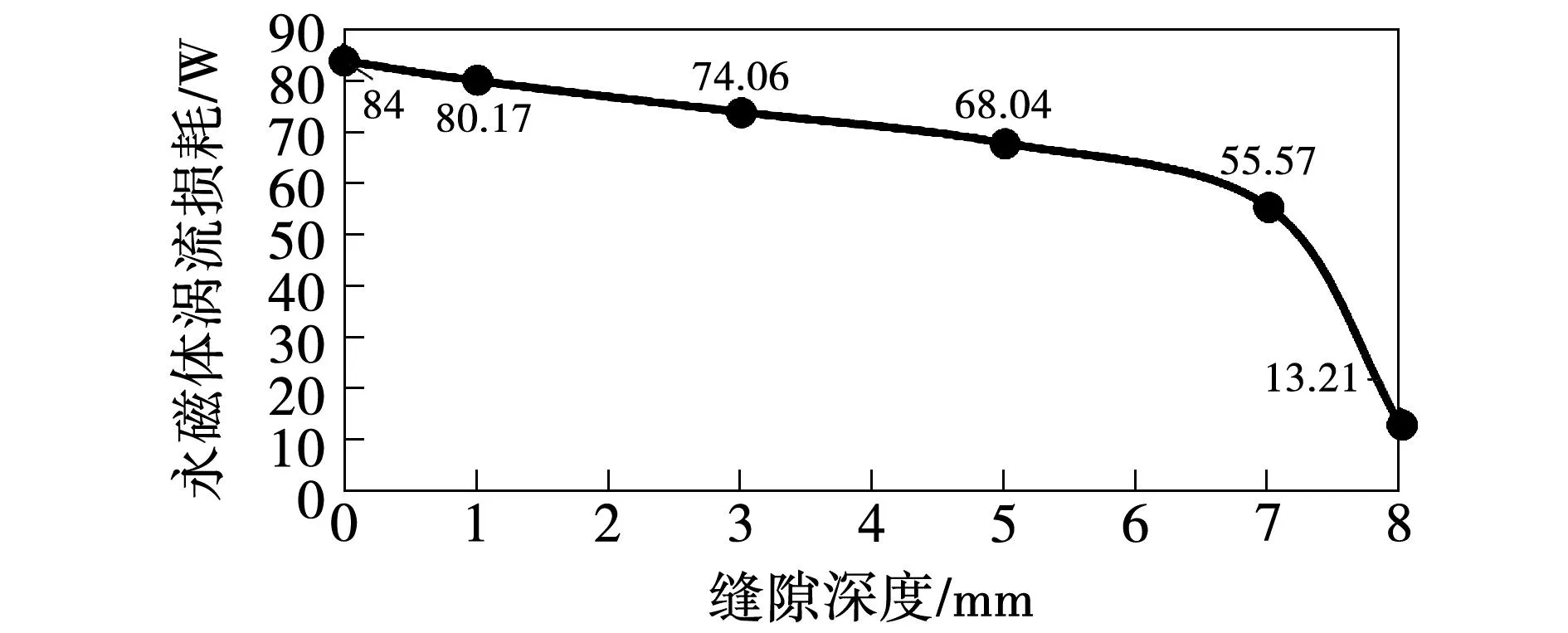
图11 不同缝隙深度下永磁体涡流损耗Fig.11 Eddy current losses of PM with different depths

由图11可知,相比于缝隙深度为8 mm即完全分块时,永磁体不完全分块对损耗的抑制效果略差,当缝隙深度分别为1、3 mm时,涡流损耗相比未切割时仅下降了4.56%、11.83%,损耗抑制效果一般。当缝隙深度达到7 mm时,涡流损耗的抑制效果有明显提升,达到了33.85%。当缝隙较浅时,损耗难以得到有限抑制,当缝隙深度接近永磁体轴向长度时,抑制效果明显增强。

图12给出了缝隙深度为7 mm时永磁体损耗与不完全分块数量之间的关系。

图12 永磁体涡流损耗随不完全分块数变化Fig.12 PM eddy current loss varies with the number of incomplete blocks

由图12可知,不完全分块数量在1～5时,损耗随着分块数量的增加而持续下降,当分块数超过5后,损耗变化范围很小。不完全分块不同分块数量下的永磁体涡流损耗分布情况如图13所示。

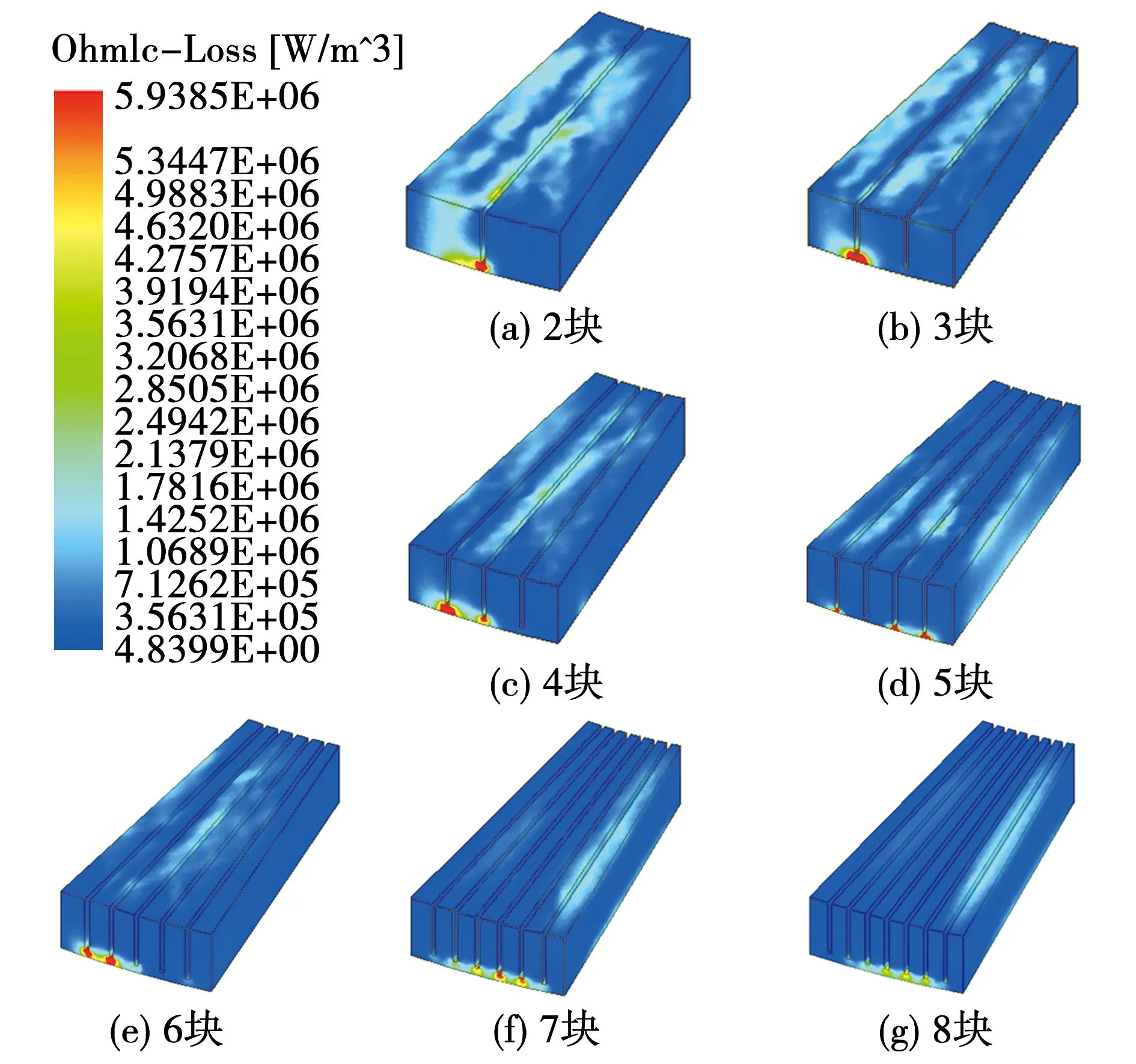
图13 永磁体涡流损耗分布随不完全分块数量变化Fig.13 Distribution of PM eddy current loss varies with the number of incomplete blocks

由图13可知,增加分块数量而引起的损耗降低主要是7 mm不完全分块区域,当分块数为5块时,不完全分块区域的涡流损耗已实现最大抑制,而未分割区域损耗不受分块数影响,轴向1 mm未分块处仍有较大损耗集中,导致不完全分块仅对部分区域有效,进而不完全分5块后损耗难以继续下降。

结合上文永磁体完全分块结果,图14最终对比了周向、径向完全分块与周向不完全分块3种情况下的损耗变化情况,组合式分块由于在分块数高于6块时其涡流损耗抑制能力才强于径向分块,对分块数量的要求较高,且可选择的分块方案较少,因此不再进行考虑。

由图可知,从损耗抑制的角度分析,同一分块数下,周向完全分块对损耗的抑制效果最彻底,径向完全分块次之,周向不完全分块抑制效果最差。但周向不完全分5块,槽深7 mm时,其损耗与径向分5块时接近,同时可以免去粘结过程。

从工艺角度分析,周向完全分块相比于径向完全分块可通过更少的分块数实现损耗的抑制,更少的分块数可降低工艺难度。而周向不完全分块因为不需要固定粘合,工艺上最容易实现。

最终确定了分块降低涡流损耗的两种方案:

1)不考虑工艺难度,对损耗抑制要求严格:周向完全分5块和6块可实现损耗的大部分抑制;

2)可抑制部分损耗并降低工艺难度:周向完全分3块/周向不完全分5块,槽深7 mm时综合效果较好。

3 磁性槽楔对永磁体涡流损耗影响

针对空间谐波引起的永磁体涡流损耗,磁性槽楔相比于传统槽楔具有更好的导磁性能,能够间接增大定子齿部的有效截面积,从而在一定程度上改善磁导波形平滑度,进而达到降低电机转子损耗的作用。

槽楔材料不同导致相对磁导率、电导率及物理性能不同,其中对电机磁场产生主要影响为相对磁导率。目前国内制备槽楔相对磁导率在5左右,国外槽楔相对磁导率不大于10[11],本文主要研究槽楔相对磁导率在1～7范围内对永磁体损耗的影响。

带槽楔电机三维模型如图15所示,为了简化计算,认为磁饱和及温度对其相对磁导率无影响,其相对磁导率近似为定值。

图15 带槽楔轴向电机三维模型Fig.15 3D model of axial motor with slot wedge

3.1 磁性槽楔对电机气隙磁场的影响

1)气隙系数计算。

气隙系数考虑了槽开口对气隙磁阻的影响,描述了气隙有效长度变化情况,下式分别计算了非导磁槽楔和磁性槽楔的气隙系数[12]:

(5)

(6)

(7)

式中:t1为齿距;bt为齿宽;μk为槽楔相对磁导率;kδμk为气隙系数;δ为气隙长;ε为修正系数。

槽楔相对磁导率为1～7下的气隙系数计算结果如表4所示。

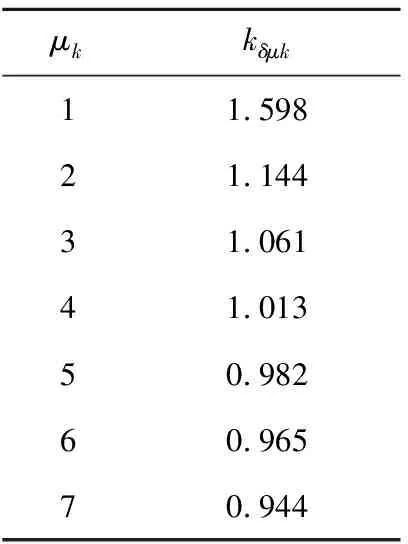
表4 槽楔不同相对磁导率下的气隙系数Table 4 Air gap of slot wedges with different permeability

由表4可知,气隙系数随槽楔相对磁导率的增加而下降,气隙系数的降低代表了气隙有效长度的缩短,进而可以削弱电机的齿槽效应。

2)气隙磁密。

在正弦供电下对槽楔相对磁导率为1～7的气隙磁密进行分解,选取前9次谐波进行分析,槽楔采用不同相对磁导率时谐波含量变化如图16所示。

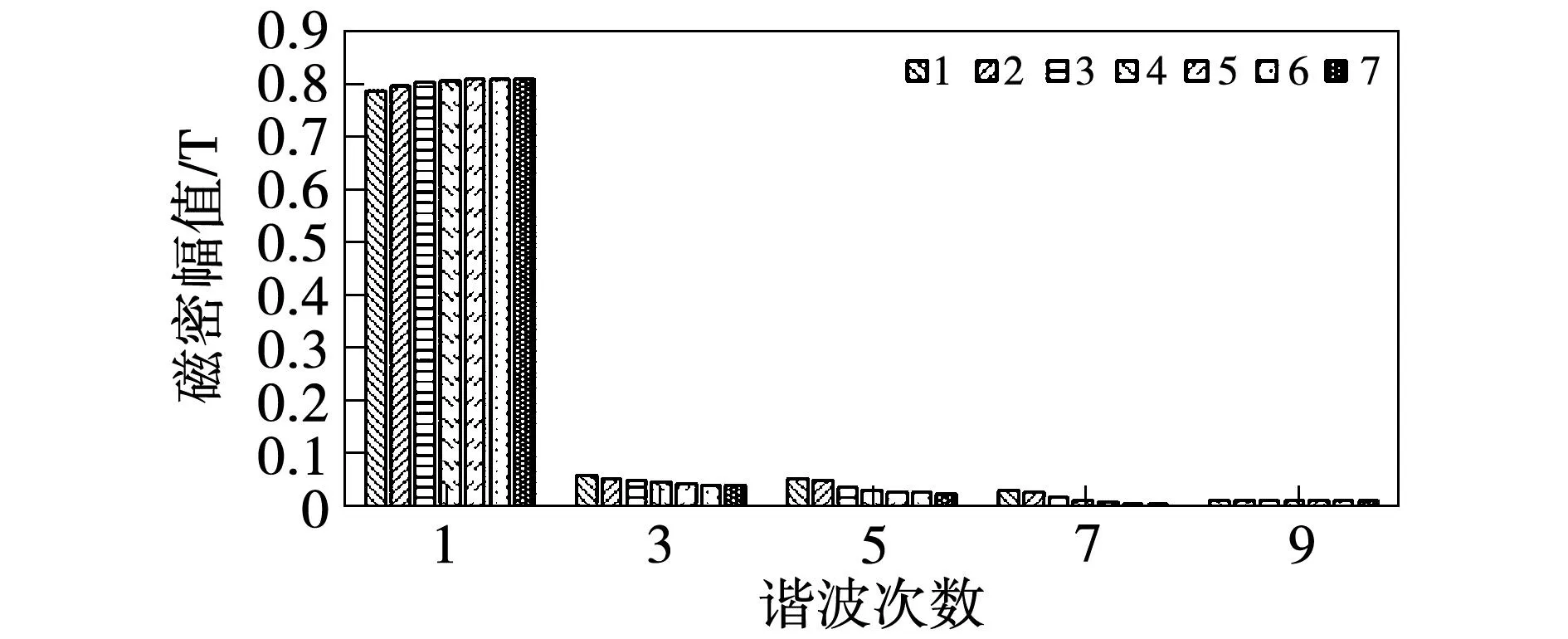
图16 不同槽楔相对磁导率下气隙磁密分解Fig.16 Air-gap magnetic density decomposition under different relative permeability of slot wedges

由图可知,定子采用磁性槽楔后,除基波略有增加,各次谐波均受到了不同程度的抑制,并且槽楔相对磁导率越高,对谐波的抑制作用越明显。

3)定子槽漏抗。

定子带槽楔示意图如图17所示。

图17 定子带槽楔示意图Fig.17 Schematic diagram of stator with slot wedge

其中定子槽h2部分的漏磁链[13]为

(8)

当未放置槽楔时,定子槽h1部分漏磁链为

(9)

总漏磁链为

(10)

总的槽漏抗为

(11)

式中:N为导体数;μ0为真空磁导率;l为铁心轴向长度;i为定子电流;f为电机频率。

定子槽口处嵌入磁性槽楔后,总漏磁链为

(12)

嵌入槽楔后的总漏抗变为

(13)

嵌入槽楔前后定子槽漏抗比值为

(14)

由于μr恒大于1,因此定子嵌入槽楔前后漏抗比值K也会恒大于1,槽楔增大了定子槽漏抗。根据式(15)～式(20)[14],采用有限元与能量法相结合计算得出的槽漏抗标幺值如表5所示。

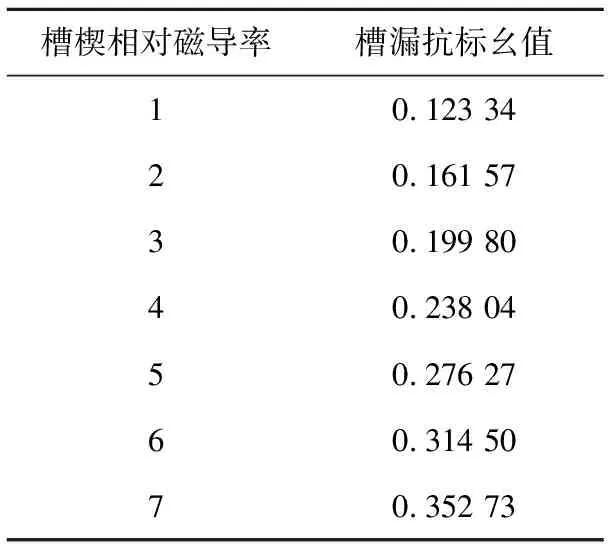
表5 槽楔不同相对磁导率下槽漏抗标幺值

磁场总能量为

(15)

令Ls=L-M,Ls为定子每相槽漏感,得到

(16)

由式(16)可知,通过有限元仿真求出磁场总能量Wm后,即可求出定子每相槽漏感。

定子槽漏抗为

Xs=ωLs。

(17)

由式(16)和式(17)可得

(18)

定子侧参数阻抗基值为

(19)

定子槽漏抗标幺值为

(20)

由表5可知,随着槽楔相对磁导率的增加,槽漏抗也随之增加,过大的槽楔相对磁导率将使电机的转矩和效率降低。

3.2 磁性槽楔对永磁体涡流损耗的抑制作用

通过求解瞬态电磁场,求得正弦供电下永磁体涡流损耗随槽楔相对磁导率变化如图18所示,其中槽楔电导率均参照不锈钢电导率1 100 000 S/m。

图18 永磁体涡流损耗随槽楔相对磁导率变化Fig.18 Eddy current loss of permanent magnet varies with relative permeability of slot wedge

由图18可知,磁性槽楔的应用对永磁体涡流损耗实现了有效抑制,随着槽楔相对磁导率的增加,对损耗的抑制能力在不断下降。相对磁导率在2～4时损耗下降幅度较大,其中相对磁导率在2时,损耗下降幅度最大,达到了55.02%,相对磁导率超过4后,损耗曲线开始趋于平稳。

槽楔相对磁导率保持为4,不同槽口宽度下采用磁性槽楔前后的永磁体涡流损耗计算结果如图19所示。

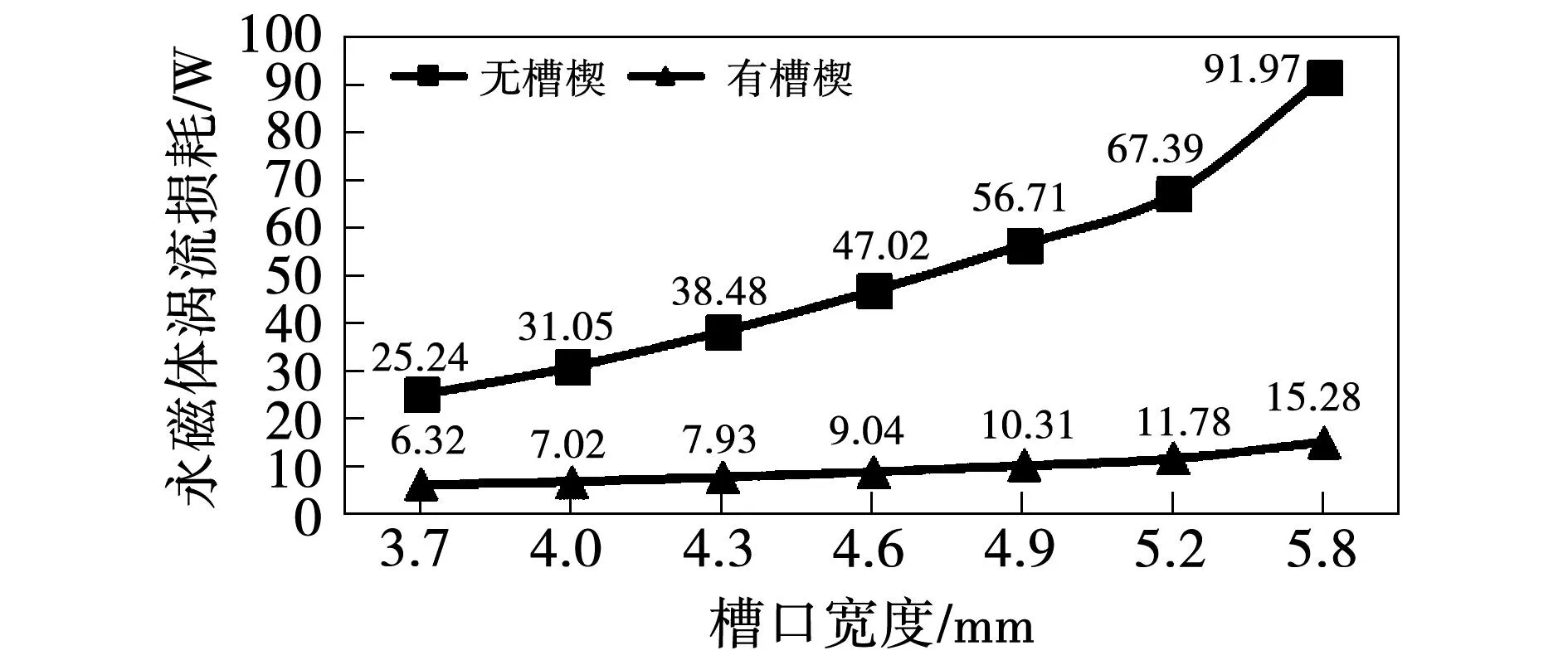
图19 不同槽宽下应用磁性槽楔对永磁体涡流损耗的影响Fig.19 Influence of slot wedge on permanent magnet eddy current loss with different slot widths

由图19可知,在未使用磁性槽楔时,槽宽由3.7 mm增加到4.6 mm,永磁体涡流损耗上升了86.31%;槽宽由3.7 mm增加到5.8 mm,永磁体涡流损耗上升了264.39%。在磁性槽楔应用后,不同槽宽下的永磁体涡流损耗均有所下降,并且随着槽口的增大,磁性槽楔对永磁体涡流损耗的抑制能力在不断增强。

槽口尺寸的增加一方面增强了不均匀气隙磁导,导致永磁体涡流损耗增加,另一方面也增加了槽楔截面积,使得更多的磁通可以通过槽楔进入气隙中,2种原因对永磁体损耗的影响程度不同。槽楔在较大尺寸槽口中降低损耗的作用会更加明显。

电机极数不变,不同槽数下采用磁性槽楔前后的永磁体涡流损耗计算结果如图20所示,为了便于对比,保证不同极槽配合下槽口宽度一致。

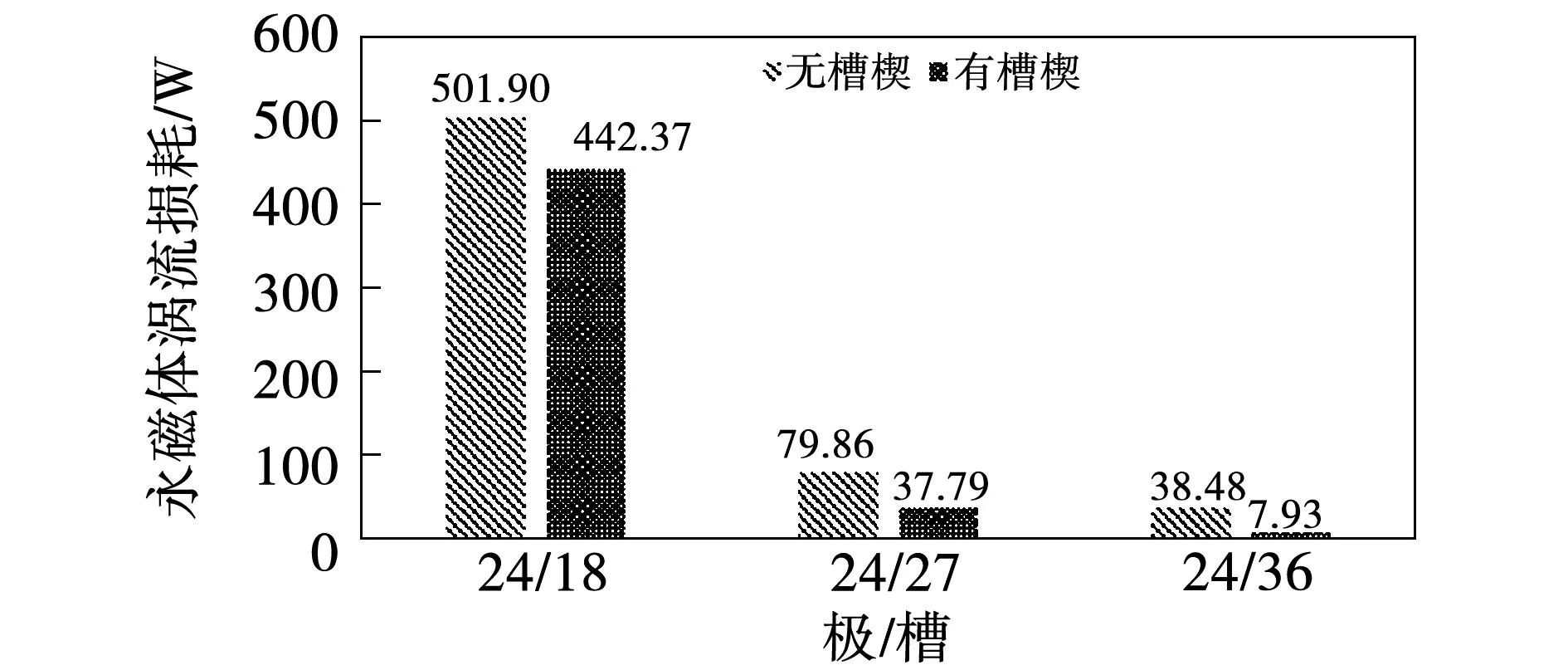
图20 不同槽数下应用磁性槽楔对永磁体涡流损耗的影响Fig.20 Influence of magnetic slot wedge on permanent magnet eddy current loss with different number of slots

由图可知,槽楔相对磁导率为4时,极数不变,不同槽数下其涡流损耗均有所下降,但永磁体涡流损耗下降率不同。在保证极数不变槽数增加时,磁性槽楔对永磁体涡流损耗的抑制作用随槽数的增加而增强。

槽口宽度不变时,随着槽数的增多,槽楔的应用数量也随着增多,相当于增加了槽楔总的截面积,相比于少槽结构,更多的磁通会通过槽楔进入空气,相当于进一步增大了齿部截面积,从而对涡流损耗的抑制作用更加明显。

3.3 磁性槽楔涡流损耗计算

磁性槽楔由于其导磁导电特性,自身也会感生出涡流,产生涡流损耗。槽楔损耗主要与其电导率和磁导率有密切关系,本文首先以不锈钢电导率σ=1 100 000 S/m为基准,在槽楔磁导率为4的前提下,分别计算了槽楔电导率在0.4σ～1.6σ内的槽楔损耗,计算结果如表6所示。

表6 不同电导率下槽楔损耗计算值

由表6可知,随着槽楔电导率的增加,涡流损耗也随之增加。由于槽楔电导率仅对自身损耗影响较大,对于气隙磁导的改善几乎无影响,因此,为避免损耗过高,磁性槽楔应尽可能选取高电阻材料。

相对磁导率是影响槽楔损耗的另一因素,在电导率均为不锈钢电导率时,槽楔不同相对磁导率下的损耗结果以及与永磁体损耗的对比如图21所示。

图21 槽楔不同相对磁导率下各项损耗对比Fig.21 Comparison of various losses of slot wedges with different relative permeability

由图21可知,随着槽楔相对磁导率的提高,永磁体损耗降低值难以抵消槽楔损耗增长值导致总损耗值增加。其中槽楔相对磁导率在2时,总的涡流损耗有一定下降,避免了总损耗过高,同时永磁体涡流损耗下降率最高,下降了55.02%,但缺点是永磁体仍存在部分损耗。

槽楔相对磁导率在4时,永磁体涡流损耗相比未使用磁性槽楔时下降了30.55 W,永磁体涡流损耗已经实现了有效抑制,但总的涡流损耗相比于磁导率为2时提高了27.33 W,而当相对磁导率高于4时,永磁体涡流损耗下降较少,但总的涡流损耗进一步提高,将使电机运行效率减小。

因此,针对本样机,槽楔相对磁导率控制在2～4范围内即可实现永磁体涡流损耗大幅度下降的目的,其中相对磁导率为2时综合效果最好,磁导率继续增加则会导致总损耗过高以及槽漏抗的增加。

4 结 论

本文针对非晶合金轴向电机永磁体涡流损耗抑制措施进行了三维有限元参数化研究,给出了各措施下的合理方案并进行了进一步优化。

针对轴向电机扇形永磁体给出了2种分块方案,周向完全分3块或不完全分5块可有效抑制永磁体部分涡流损耗,同时可降低装配难度。周向完全分5块和6块可抑制永磁体80%以上的涡流损耗,更适合对永磁体温升要求较高下应用。

磁性槽楔的应用有效的提高了气隙磁导平滑度,降低了电机齿槽效应。当槽楔相对磁导率在2～4时,可有效降低永磁体涡流损耗,其中相对磁导率在2时综合效果最好,同时磁性槽楔在槽数较多或槽宽较大的定子中应用更好。但槽楔相对磁导率不宜选择过高,否则会导致电机漏磁增多,同时应尽可能应用高电阻率材料来降低其自身涡流损耗。