DAB级联单相逆变器系统的阻抗特性及稳定性分析
2024-01-18刘欣袁静高鑫波
刘欣, 袁静, 高鑫波
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引 言
在光伏系统、蓄电池、超级电容,车网互联(vehicle to grid,V2G)等交流并网型储能系统中,通常需要使用两级式DC/AC变换器实现并入交流电网和双向功率控制的功能[1]。其中,双有源桥变换器由于具有高功率密度、电流隔离、能量双向传输和易实现零电压开关等优点[2-4],很好地适应了交流并网型储能系统的需求,是第一级DC/DC变换器的理想选择,而单相逆变器用于与电网连接。基于双有源桥(dual active bridge,DAB)变换器的两级式DC/AC变换器的典型电路拓扑如图1所示。该拓扑整体结构简单,易于实现,控制方法较为成熟,被大量应用于电动汽车充电桩领域[5-8]。然而,由于变换器复杂的输入输出特性以及级联结构的存在,尽管两级变换器在单独运行时能保持稳定,但子系统之间的相互作用可能会使系统性能下降,导致直流母线产生电压振荡,以至于系统崩溃[9]。因此,通过稳定性分析、合理参数调整、控制优化等方法改善级联系统的稳定性和可靠性是当今研究的一个热点与难点问题[10-12]。
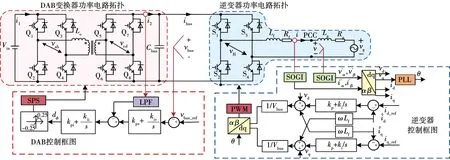
图1 两级式DC/AC变换器主电路拓扑及控制框图Fig.1 Main circuit topology and control block diagram of two-stage DC/AC converter
基于阻抗的Nyquist阻抗匹配原则[13]已经被广泛应用于各类级联系统的交互稳定性的研究中。准确的阻抗模型对于级联系统稳定性分析是必要的。目前,常用的逆变器阻抗建模方法包括谐波线性化法[14-16]和dq坐标系下的阻抗建模法[17-18]。谐波线性化将系统视为2个单输入单输出系统,主要用于分析三相系统的谐波稳定性;而dq阻抗建模法通常将电气量转变为d轴和q轴分量,以便单独控制有功和无功功率,有利于在稳态工作点处进行小信号分析。文献[19]在dq坐标系下推导了使用不同控制策略的三相并网逆变器的直流侧输入阻抗模型,此方法适用性较强,但并未应用到单相逆变器系统中。文献[20]提出一种基于二阶广义积分器(second order generalized integrator,SOGI)的dq坐标系下单相整流器的阻抗建模方法,但此方法并未推广到单相并网逆变器的阻抗建模中。
由于阻抗相互作用是造成两级式DC/AC级联系统失去稳定的根本原因,可以通过重塑源变换器或者负载变换器的总线端口阻抗来提高系统的稳定性。为了达到这一目的,学者们提出了多种方法,包括无源阻尼法[21-23]和有源阻尼法[24-26]。其中,无源阻尼法需要引入附加无源元件,以改变变换器的阻抗特性,但附加阻尼电路会增加硬件成本,降低变换器效率;有源补偿法具有成本低、不增加损耗的优点,因而被广泛用于基于DAB变换器的级联系统阻抗匹配优化设计中。文献[27]采用有源阻尼的优化思路对LC-DAB级联系统进行阻抗重塑,提出基于一次侧电容电压的并联虚拟阻抗和一次电流串联虚拟阻抗控制策略,从而使得级联系统在全功率范围内均能稳定运行;文献[28]研究基于DAB的储能系统稳定性,提出在窄带范围内对负载变换器DAB的输入阻抗进行重塑,在提高稳定性的同时保证系统动态性能良好;文献[7]研究了用于电动汽车双向充放电的DAB级联单相并网电压源变换器(voltage source converter,VSC)系统的阻抗稳定性,提出一种基于虚拟电阻的有源阻尼方法,以改变VSC的输出阻抗,提高级联系统在各种工作模式下的稳定性;文献[29]面向DAB级联三相VSG系统,通过构建与DAB转换器的输入阻抗并联或串联的虚拟阻抗以增加DAB输入阻抗幅值,从而满足稳定性准则。文献[30]针对具有电压调整单元的DAB变换器提出一种基于超前-滞后的阻抗优化调节器用以抑制输出阻抗谐振尖峰,提升了系统运行可靠性,并优化了电流应力。总的来说,上述级联系统的稳定性增强方法都需要增加附加的控制过程,从而不可避免地增加了模型的复杂度,其设计方法仍存在进一步简化的空间。而DAB变换器的输入阻抗会受到其反馈控制器的影响,揭示二者之间的关联有助于简化阻抗匹配优化设计,但此方面的相关研究较少,并且缺乏深入的理论分析。
针对上述问题,本文对双有源桥DC/DC变换器与单相并网逆变器组成的级联系统进行阻抗建模并进行稳定性分析。首先,建立采用双环控制策略的DAB输出阻抗模型和采用解耦电流控制策略的单相并网逆变器直流端输入阻抗模型,并将锁相环的相位波动考虑在内,通过扫频法验证阻抗模型的正确性。随后,建立阻抗交互模型,从理论上分析DAB变换器的PI参数对其输出阻抗波形的影响,结合Nyquist图和闭环根轨迹进一步讨论关键参数与系统稳定性之间的关联。分析结论表明,调节DAB电压外环比例系数可直接调节级联系统稳定性,基于此,提出通过优化DAB变换器的电压外环比例系数提高级联系统稳定性的方法,该方法无需任何额外的补偿器或控制回路,在兼顾系统动态性能的同时,有效实现了基于DAB的交直流级联系统的稳定性增强。MATLAB/Simulink仿真算例验证了稳定性改善方法的有效性。
1 级联系统阻抗建模
变换器阻抗的精确建模是稳定性分析的基础。图1所示的控制框图为级联系统的常规控制方案,其中,DAB变换器负责控制直流母线电压的稳定,单相并网逆变器负责控制功率输出[31-32]。本节将分别给出DAD输出阻抗和单相并网逆变器的直流侧输入阻抗的建模过程。
1.1 DAB变换器输出阻抗建模
DAB变换器的拓扑及控制方案如图1中左面虚线框所示。其输出功率[33-34]可表示为
(1)
式中:n为变压器变比;Vin为DAB输入电压;vbus为输出电压;Lo为变压器等效电感;fs为开关频率;dφ为变压器两侧H桥输出电压之间的相移量(dφ=φ/2π);i2为副边H桥输出电流,〈i2〉表示其平均值。经小信号分析可得i2与占空比dφ的关系为
(2)
式中符号^表示变量的小信号形式。
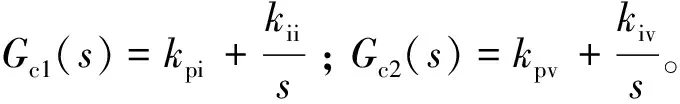
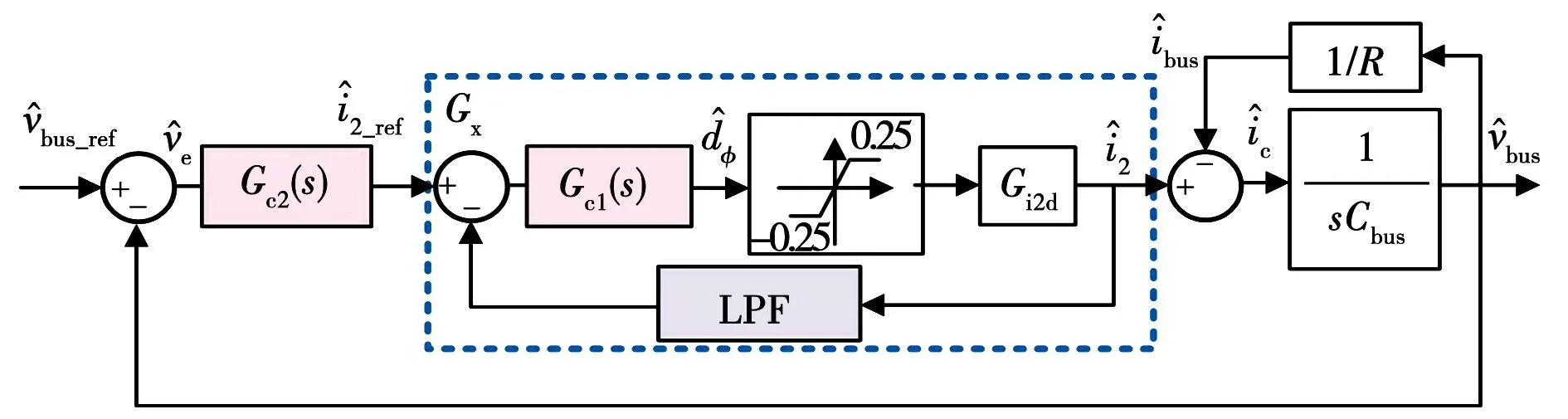
图2 DAB控制回路小信号模型Fig.2 Small signal model of DAB control loop
根据上述控制框图,得到DAB的输出阻抗为
(3)
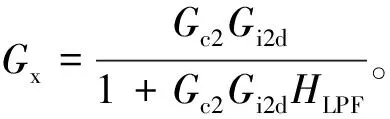
1.2 单相并网逆变器直流侧输入阻抗建模
基于SOGI的锁相环(PLL)模型如图3(a)所示。图中,v为自公共耦合点(PCC)电压(将其本身视为静止坐标系下的α轴分量,β轴虚拟分量与之垂直)。SOGI的传递函数为
(4)

图3 基于SOGI的PLL模型Fig.3 SOGI-based PLL model
式中:ω1为电网工频;KSOGI为闭环系数。
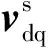
根据图1可得系统功率方程为:
(5)
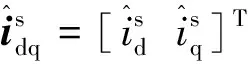

(6)

同理可得输出电流与占空比的“控制量”与“电气量”的小信号关系为:
(7)
式中:
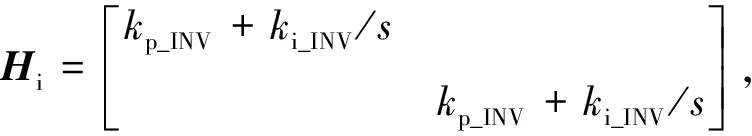
将解耦电流控制策略与PCC电压前馈结合,得到考虑锁相环影响的逆变器控制回路的小信号模型如图4所示。

图4 PLL影响下电流控制回路小信号模型Fig.4 Small-signal model for current control loop with PLL
根据图4,得到逆变器控制部分的方程为
(8)
联立式(5)、式(8)可得单相并网逆变器直流侧输入导纳为
(9)

相应的单相并网逆变器直流侧输入阻抗为
Zin_INV=1/Yin_INV。
(10)
1.3 阻抗模型的仿真验证
基于MATLAB/Simulink平台搭建了DAB级联单相并网逆变器的仿真模型,采用扫频法对2个级联子系统的输出和输入阻抗模型分别进行验证,仿真参数如表1所示。图5给出了仿真扫频与理论模型的对比结果。可以看出,在1~10 000 Hz频段,所得阻抗模型与扫频结果吻合较好,验证了所推得的DAB输出阻抗和单相逆变器输入阻抗模型的正确性。
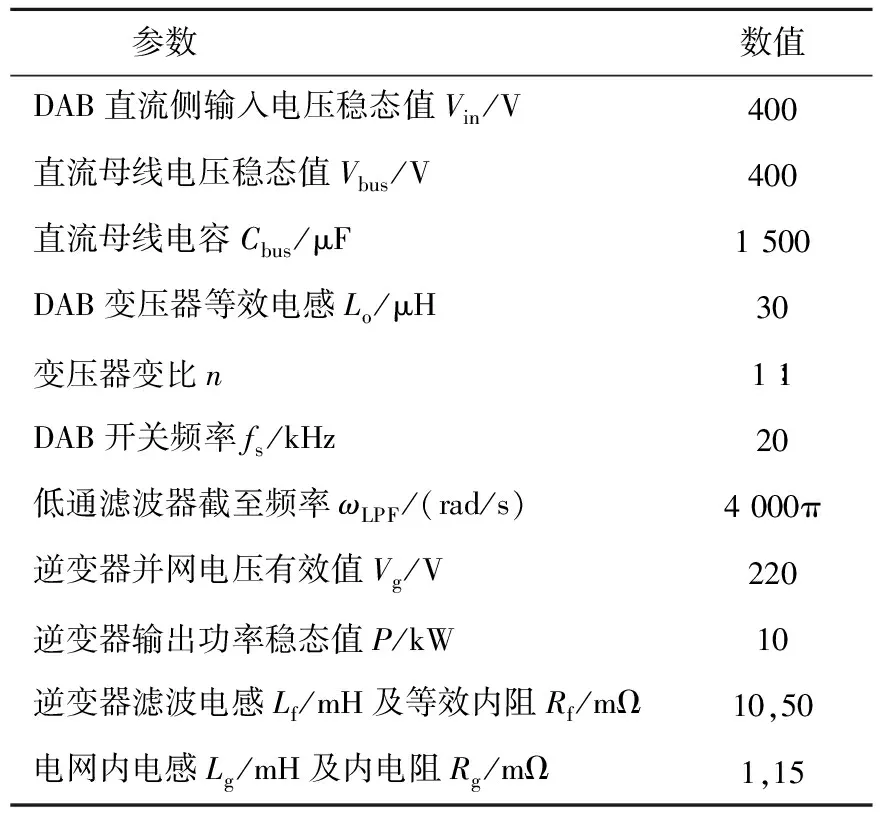
表1 级联系统电路参数Table 1 Parameters of cascade system
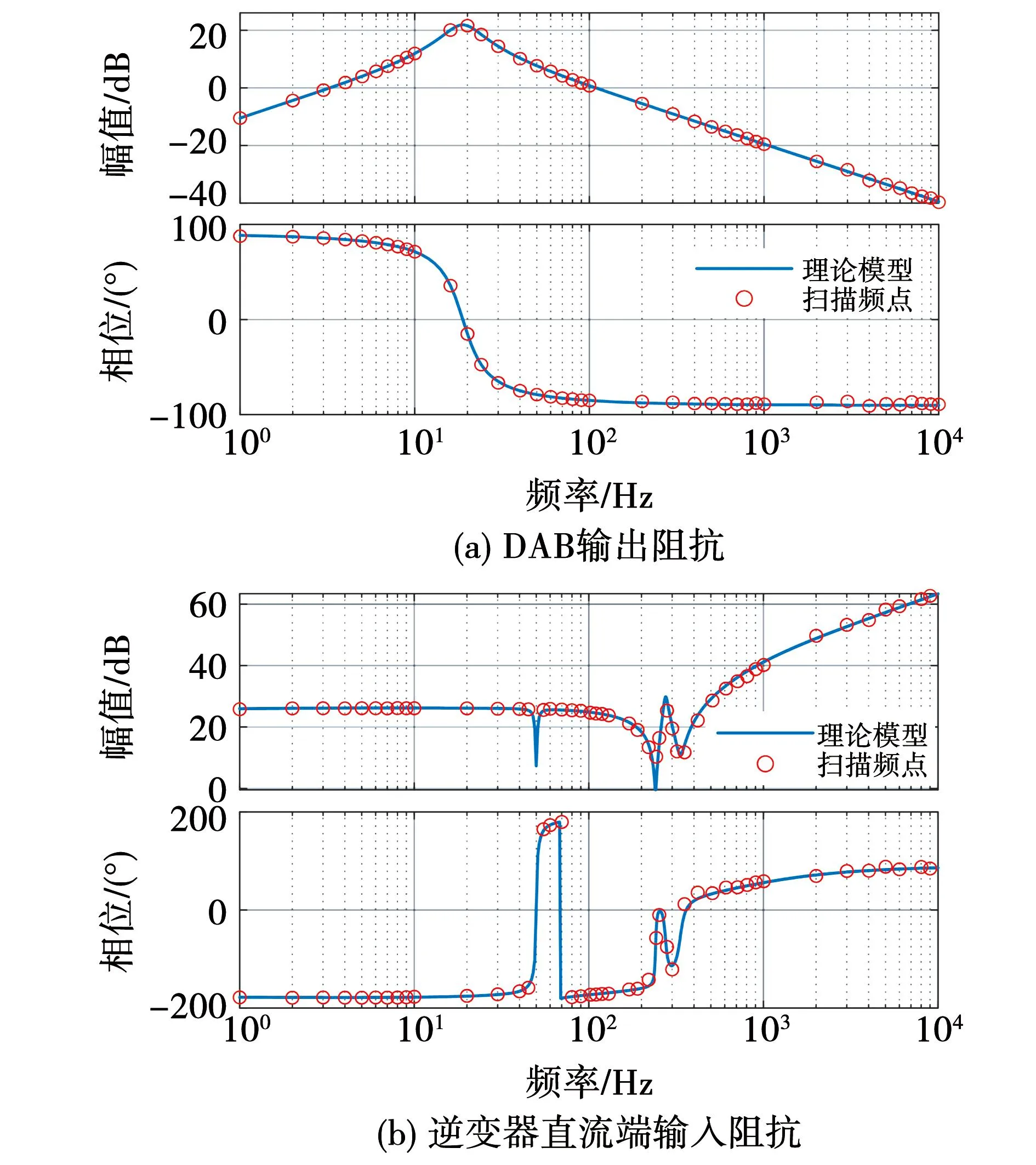
图5 级联系统阻抗模型Fig.5 Impedance model of cascade system
2 级联系统稳定性分析
2.1 级联系统阻抗交互模型
级联系统的稳定性不仅取决于变换器各自的稳定性,还决定于源变换器(本文为DAB)输出阻抗与负载变换器(本文为单相逆变器)输入阻抗二者交互作用的影响。将DAB视为电压源,逆变器视为电流源,二者构成的级联系统阻抗相互作用示意图如图6所示。

图6 级联系统等效阻抗示意图Fig.6 Equivalent impedance diagram of cascade system
根据图6,可知级联系统开环传递函数为
(11)
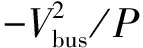
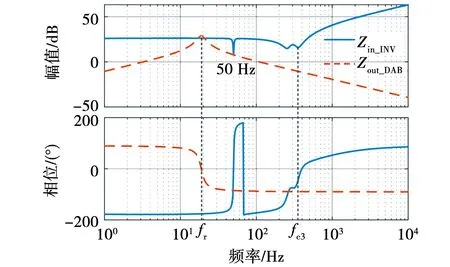
图7 级联系统阻抗伯德图Fig.7 Impedance Bode diagram of cascade system
综合以上阻抗特性可知,DAB输出阻抗的谐振峰以及逆变器在低频段的负阻抗特性是导致交直流级联系统稳定性降低的主要原因。一旦DAB输出阻抗的谐振峰与逆变器输入阻抗发生交叉,就会因相位裕度无法满足稳定条件而造成系统振荡失稳。
2.2 DAB变换器的控制参数分析
由图7可知,平抑DAB输出阻抗的谐振峰将有效提高级联系统稳定性。为了达成这一目的,本节将详细分析DAB反馈控制器的PI参数与谐振峰之间的关联,为级联系统的稳定性分析及控制器参数优化设计奠定基础。
当DAB电流内环截止频率与一阶低通滤波器LPF带宽相等时,经控制器定量设计可得电流控制器比例系数kpi为0。将kpi=0代入式(3),并且忽略含有Cbus和TLPF的高阶项,整理得到DAB输出阻抗的简化表达式为
(12)
图8给出了DAB输出阻抗的理论模型和简化模型的对比图。可以看出,在1~200 Hz频率范围内,二者阻抗模型基本吻合,结合图7可知,影响系统稳定性的频段为几十赫兹,因此说明上述简化模型可胜任稳定性分析需求。

图8 DAB理论模型和简化模型对比Fig.8 Comparison of theoretical and simplified Bode diagrams of DAB
设定DAB电流内环截至频率fc1为2 000 Hz,相位裕度Pm1为45°,同时电压外环截至频率fc2为20 Hz,相位裕度Pm2为45°时,经设计所得DAB的控制参数如表2所示。
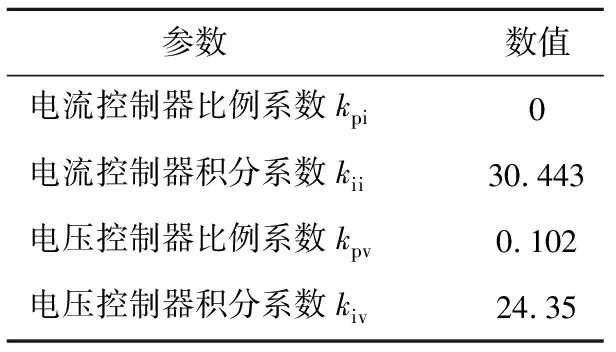
表2 DAB控制器PI参数Table 2 PI parameters of DAB controller
将s=jω代入式(12),得到DAB阻抗的模值为
(13)
式中a=Gi2dkii。
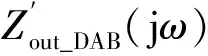
(14)
根据式(13)和式(14)可得DAB输出阻抗的谐振频率及谐振峰值分别与控制参数的关系曲线如图9所示。结合式(27)、式(28)和图9,可得如下结论:当电压外环比例系数kpv增大时,谐振频率几乎不变,谐振峰值陡然降低;当电压外环积分系数kiv增大时,谐振频率增大,谐振峰值维持不变;当电流环积分系数kii改变时,二者均基本不发生改变。上述分析表明,参数kpv是平抑DAB输出阻抗谐振峰的关键参数,而参数kiv是改变谐振频点的关键参数。
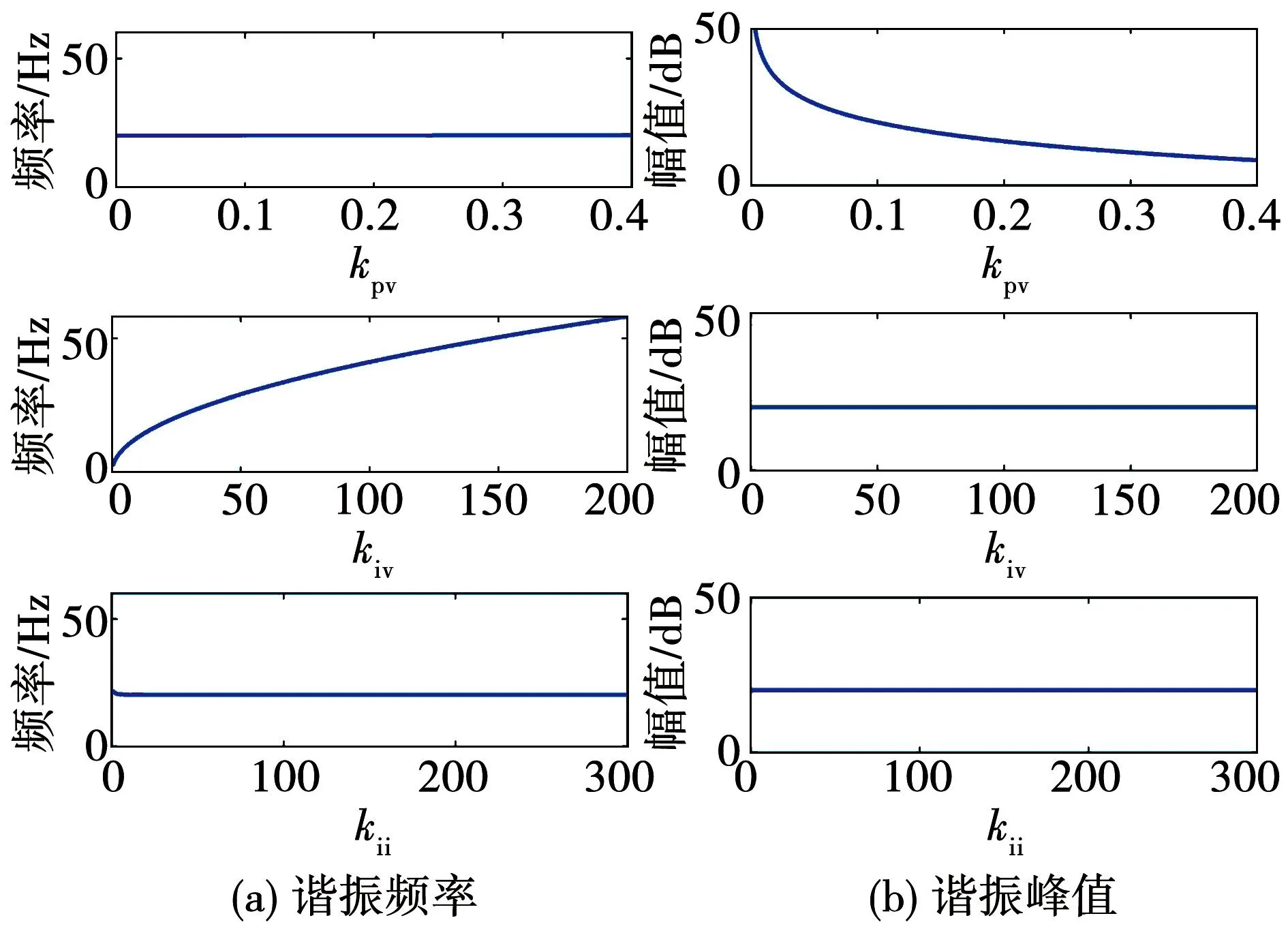
图9 谐振频率及谐振峰值与DAB控制参数的关系曲线Fig.9 Relationship curves of resonant frequency and resonant peak with DAB control parameters
为了佐证此结论,图10给出了不同控制参数下的DAB输出阻抗伯德图。可以看出,当比例系数kpv从0.02逐渐增大到0.4,且其余参数与表1和表2保持一致时,DAB输出阻抗谐振峰值急剧减小,但谐振频点基本保持不变;当积分系数kiv从10增大到120,且其余参数与表1和表2保持一致时,DAB输出阻抗谐振频率逐渐增大,而谐振峰值几乎不变。
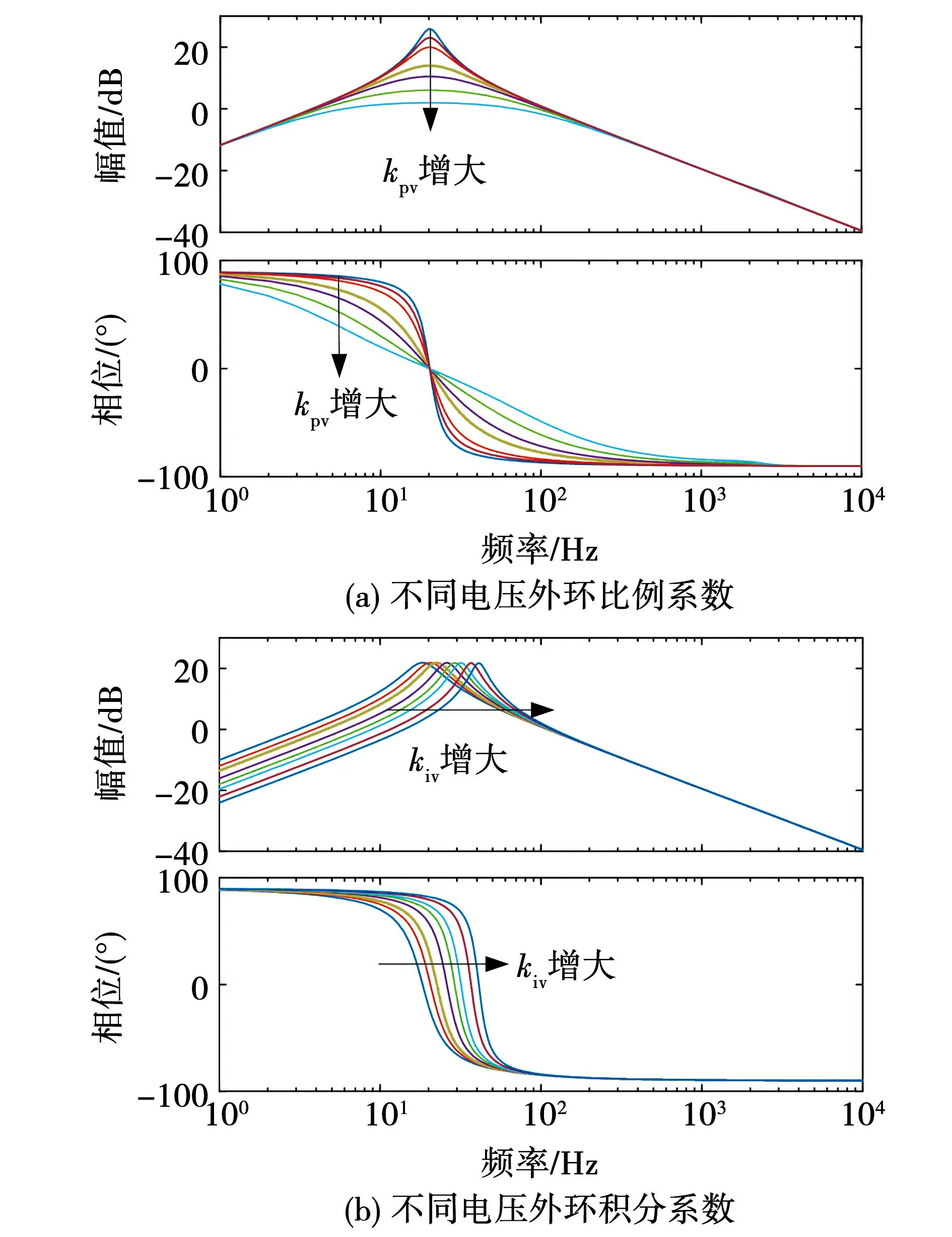
图10 不同控制参数作用下DAB输出阻抗伯德图Fig.10 DAB output impedance Bode diagram of different control parameters
综上所述,DAB电压外环控制器参数直接决定了其输出阻抗谐振峰值的大小及位置。其中,参数kpv与谐振峰幅值大小具有强相关性,适度增大参数kpv将显著降低DAB输出阻抗谐振峰,从而避免与逆变器输入阻抗发生交叉。据此可推断,参数kpv是作为影响级联系统稳定性的关键参数,对其进行优化设计可实现系统稳定控制,且设计过程也最为简单,相关分析及验证将在2.3节给出。
2.3 DAB电压外环比例系数对系统稳定性的影响
本节进一步讨论kpv对级联系统稳定性的影响。
根据式(11)可知系统的特征方程为
1+Tm=0。
(15)
将式(3)和式(10)代入式(15),可得
(16)
由于参数kpv直接体现在系统特征方程中,因此可结合基于闭环传递函数的根轨迹和开环传递函数的Nyquist图进行分析。
对式(16)进行等效变换,保证特征方程不变,得到系统等效的开环传递函数为
(17)
根据式(17),得到当参数kpv从0逐渐变化至+∞时系统闭环传递函数的特征根在复平面的变化轨迹如图11所示。此时DAB电流内环控制参数与表2中相同,电压外环积分系数为98.3。可以看出,当kpv<0.063 4时,级联系统存在右半平面极点,系统处于不稳定状态;当kpv>0.063 4时,系统方可稳定;当kpv=0.063 4时,复平面上出现位于虚轴上的闭环极点(0,±j251),说明系统处于临界稳定状态,这意味着系统中将会出现251 rad/s(约40 Hz)的振荡频率。
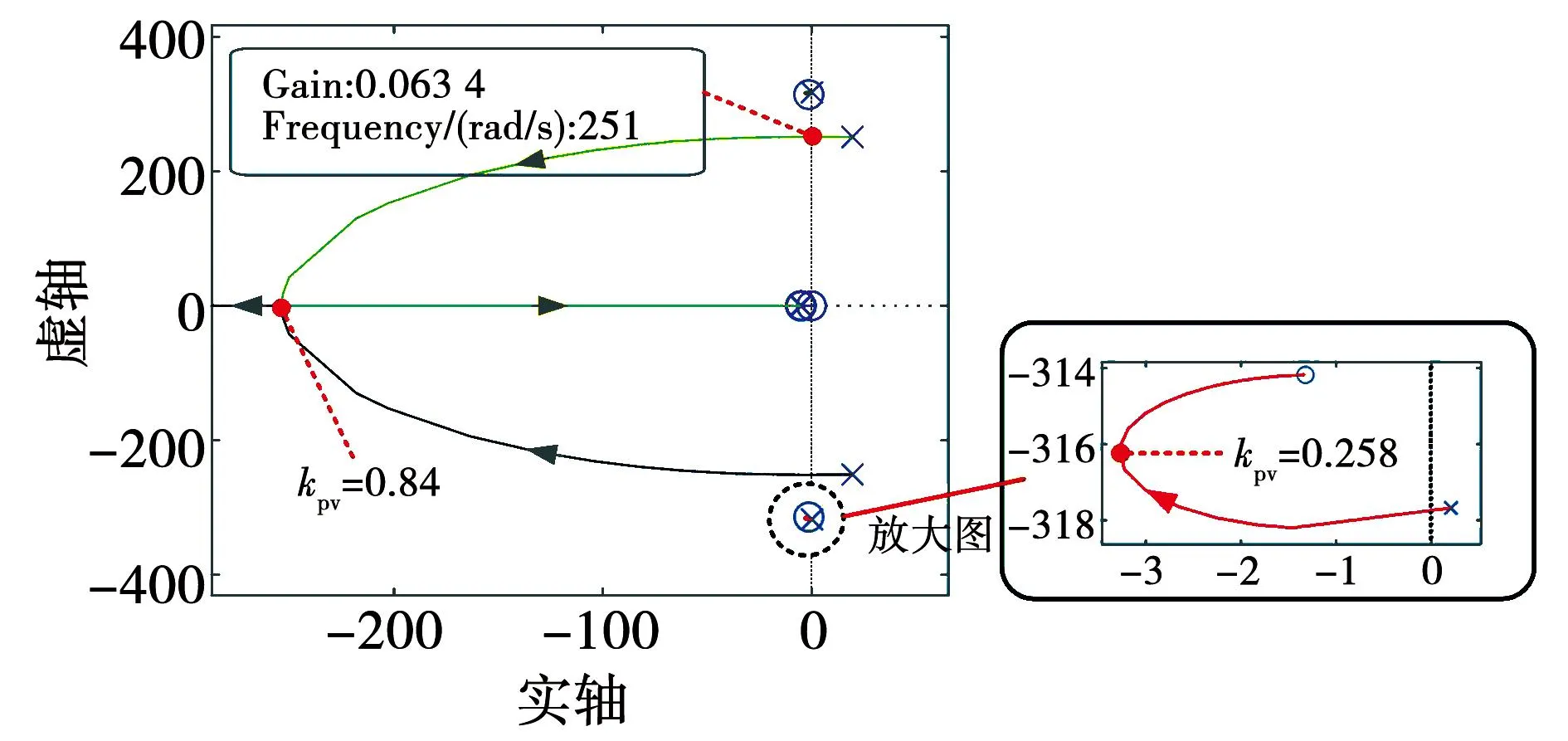
图11 系统关于参数的kpv的根轨迹图 Fig.11 Root trajectory diagram of the system with respect to the parameter kpv
图12给出了此临界稳定状态下系统开环传递函数Tm的Nyquist图,在此参数状态下,Nyquist曲线恰好穿越(-1,j0)点。分析结果说明,增大DAB电压外环比例系数kpv有助于增强级联系统稳定性,反之,将使级联系统稳定性变差。
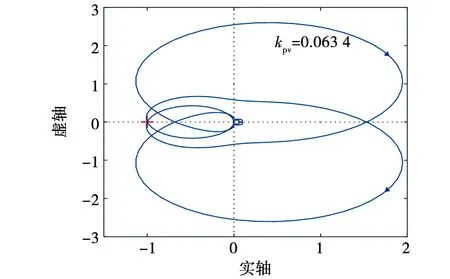
图12 系统开环传递函数的Nyquist图Fig.12 Nyquist diagram of the open-loop transfer function
为了验证上述分析结论,在MATLAB/Simulink中搭建DAB与单相并网逆变器级联系统的仿真模型。电路参数如表1所示。图13给出了当其余参数保持不变,DAB电压外环比例系数kpv分别为2、0.258、0.063 4和0.03时直流母线电压和交流侧输出电流的时域仿真波形。可以看出,当kpv为2和0.258时,系统运行在稳定状态;当kpv为0.063 4时,系统处于临界稳定状态;当kpv减小到0.03时,系统振荡失稳。这与图11中的参数根轨迹分析结果相符。
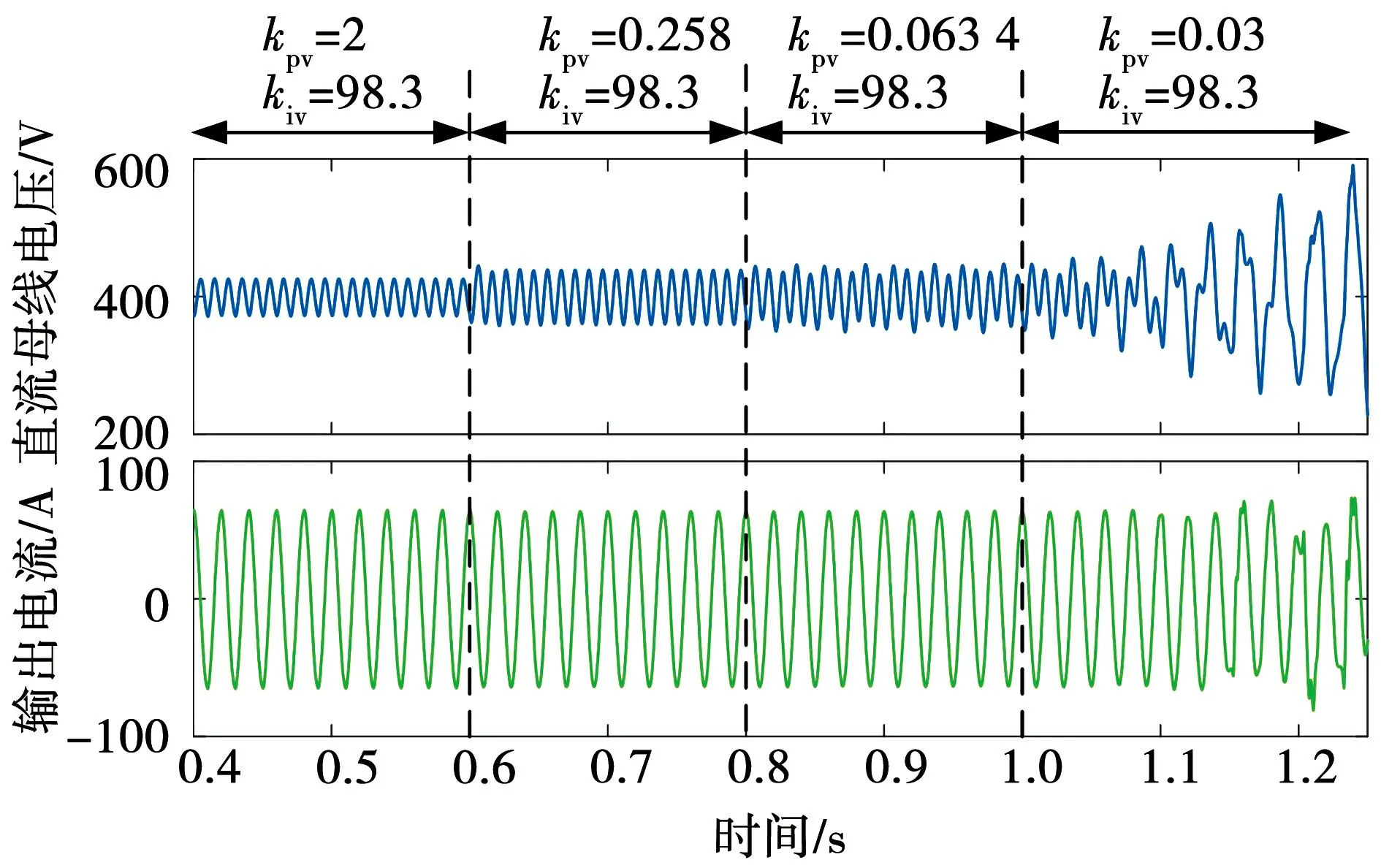
图13 kpv减小时直流母线电压和交流电流时域波形Fig.13 Waveforms of DC bus voltage and AC current when kpv decreases
取时间窗为0.2 s,对图13中各个时间段的直流母线电压的时域波形进行频谱分析,所得结果如图14所示。可以看出,当kpv>0.063 4时,直流母线电压主要含有直流分量和单相交直流系统中固有的二倍频分量;当kpv=0.063 4时,在直流母线电压中出现可观的40 Hz频率分量,与图11中临界稳定状态下的系统振荡频率基本吻合;当kpv<0.063 4时,直流母线电压中谐波分量杂乱繁多,系统失去稳定性。

图14 直流母线电压FFT分析Fig14 FFT analysis of DC bus voltage
此外,还需特别说明的是,系数kpv在影响系统稳定性的同时,也会影响系统动态响应速度。观察图11中根轨迹局部放大图可知,当kpv小于0.258时,随着kpv增大,主导极点的根轨迹从右半平面逐渐变化到左半平面并远离虚轴;当kpv大于0.258时,根轨迹方向转变并逐渐靠近虚轴。因此,当kpv=0.258时,系统具有最佳的动态性能。若kpv持续增大,越过最佳运行点,虽仍可保证稳定,但系统稳定速度将滞缓,这说明需兼顾稳定性和动态性能进行kpv的参数设计。
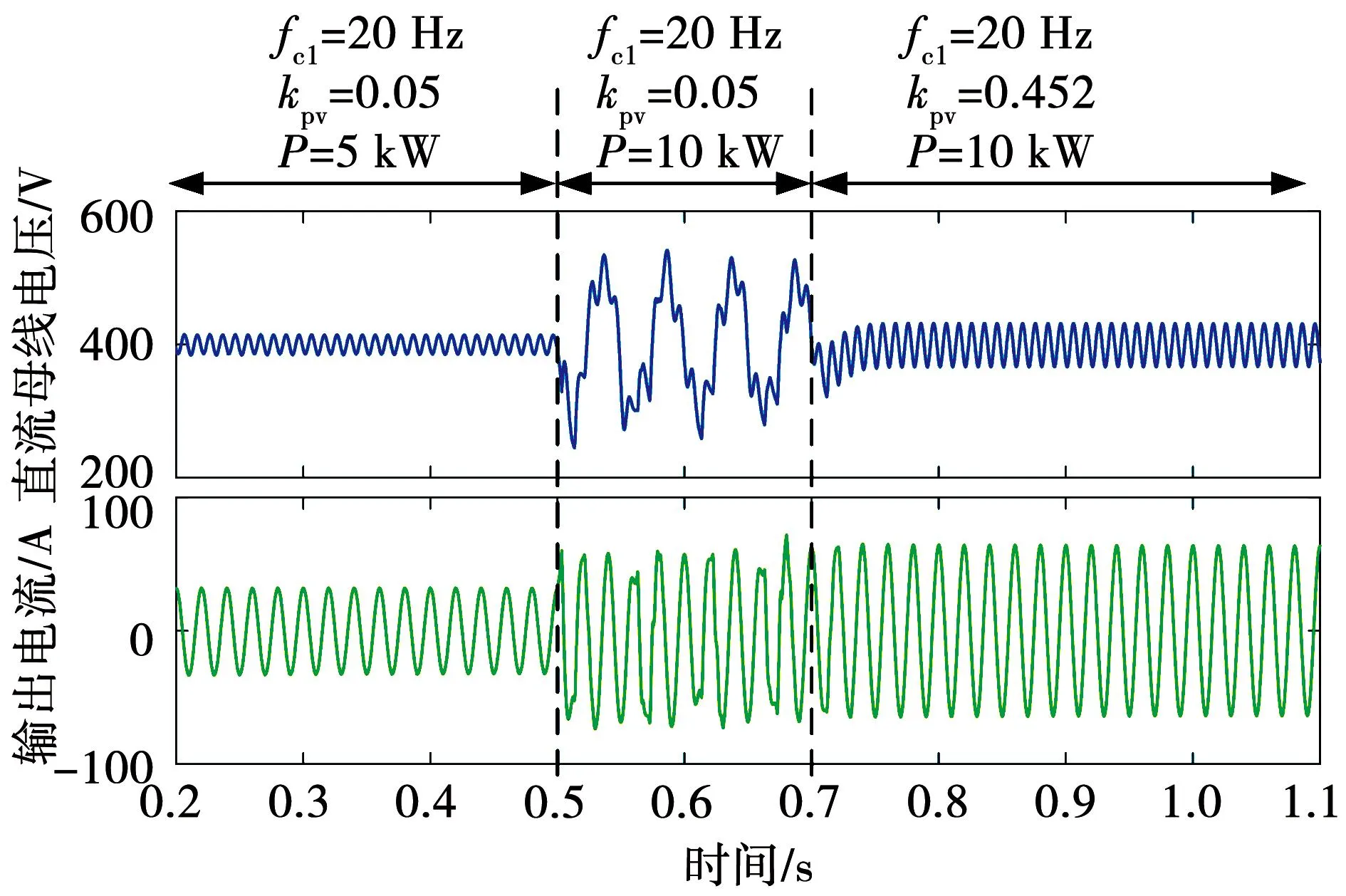
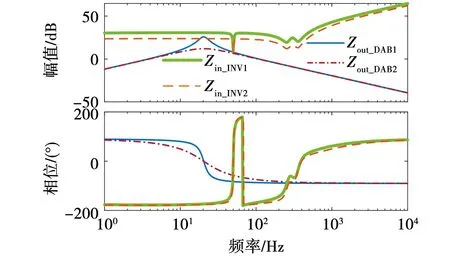
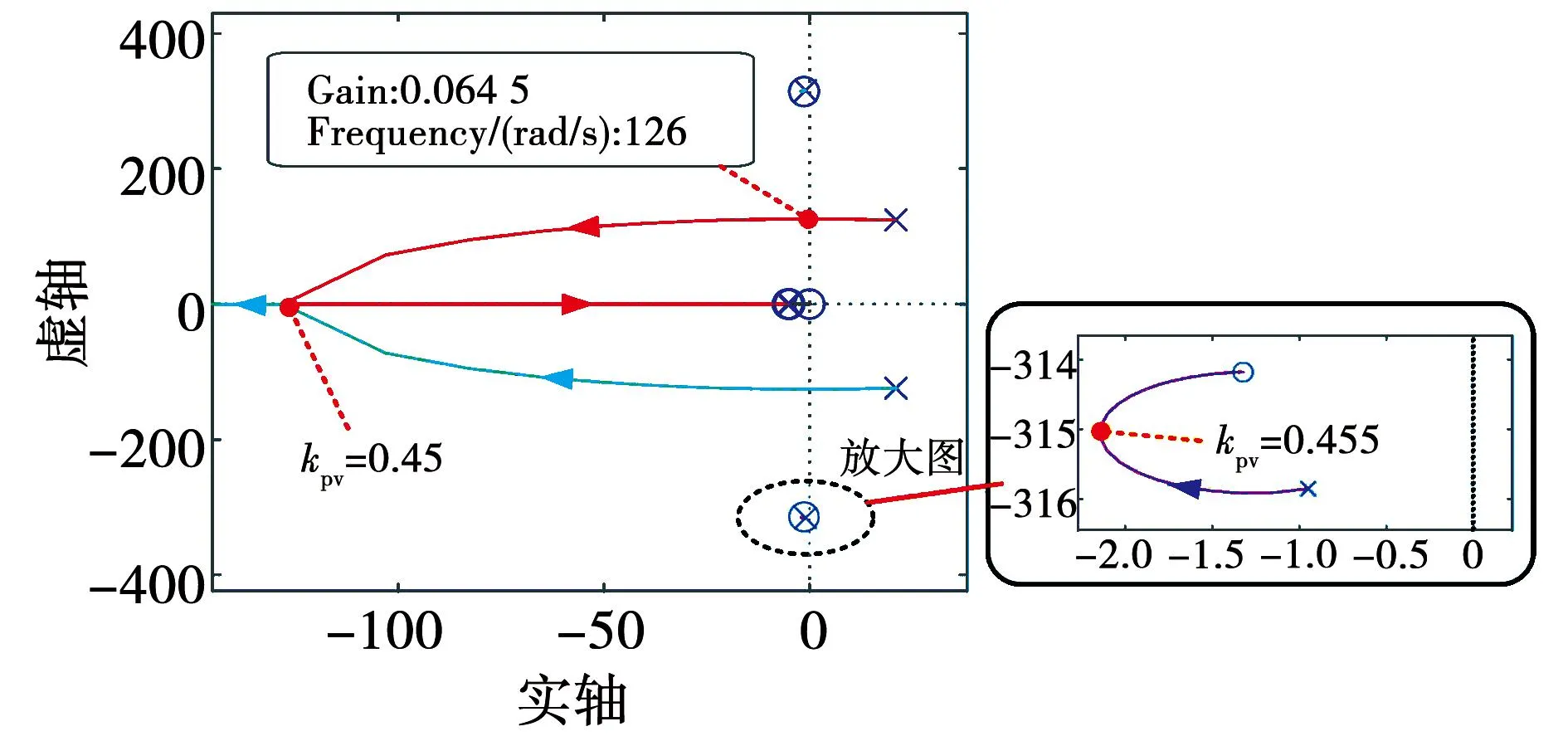
为了验证这一结论,图15给出了kpv取值变化时系统有功功率波形的变化,从有功功率角度说明系数kpv对系统稳定性及动态响应速度的影响。比较图15(a)、(b)和(c)可知,当0.063 4 图15 不同kpv作用下的有功功率曲线Fig.15 Active power waveforms with different kpv 第2.3节中的分析结论表明,增大DAB电压外环比例系数kpv将显著提高级联系统稳定性。因此,当级联系统面临振荡失稳问题时,一种简单而可靠并且无需任何额外的补偿器或控制回路的稳定性改善方法为:增大DAB电压外环比例系数kpv。 图16给出了算例中直流母线电压和交流电流时域波形,图17则给出了与之对应的级联系统阻抗伯德图。如图16中0.2~0.5 s时间窗内波形所示,当系统传输功率为5 kW时,系统稳定运行,直流母线电压包含400 V的直流分量和二倍频分量。若传输功率增加为10 kW,系统将发生振荡失稳,如图16中0.5~0.7 s的波形所示。图17中曲线Zin_INV1与Zin_INV2分别为功率改变前后逆变器输入阻抗伯德图。可以看出,负载的加重造成逆变器在低频段的阻抗幅值减小,因此与DAB输出阻抗发生交叉。 图16 稳定性改善前后的时域仿真波形Fig.16 Time domain simulation waveforms before and after stability improvement 图17 稳定性改善前后的级联子系统阻抗伯德图Fig.17 Impedance Bode diagram before and after stability improvement of the cascade subsystem 为了改善系统稳定性,应当增大DAB电压外环比例系数。图18为传输功率为10 kW时,级联系统关于参数kpv的根轨迹曲线。可以看出,要想保证系统稳定运行,kpv的取值必须大于0.064 5,并且当kpv取0.452时,系统具有最佳动态性能。观察图16中0.7~1.1 s时域波形可知,在0.8 s时,将DAB电压外环比例系数调整为最佳参数0.452,其余参数保持不变,由于DAB输出阻抗的谐振峰值降低,系统又重新恢复至稳定运行状态。 图18 传输功率为10 kW时系统闭环根轨迹Fig.18 Closed-loop root trajectory of the system at 10 kW transmission power 上述仿真算例进一步验证了稳定性改善方法的可行性。在系统控制器设计中,应当根据DAB和单相并网逆变器的阻抗特性,利用阻抗伯德图和系统关于参数kpv的闭环根轨迹进行直观判断,综合考虑系统的稳定性和动态响应速度,以确定适合的控制参数。 本文分别建立了DAB输出阻抗模型和考虑锁相环相位波动影响的单相并网逆变器的直流端输入阻抗模型,提高了模型的准确度,并通过扫频法对阻抗模型进行验证;此外,通过理论分析获得了DAB输出阻抗谐振频率及谐振峰值的计算公式,从原理上解释了DAB的电压外环比例系数kpv是影响输出阻抗谐振峰值的关键参数,且增大kpv能显著降低DAB输出阻抗谐振峰值;在此基础上,结合Nyquist图和系统闭环根轨迹进一步讨论kpv与系统稳定性之间的关联,综合分析了kpv对级联系统稳定性和系统动态性能的影响,进而提出了一种兼顾动态性能的级联系统稳定性改善方法。结合Simulink时域仿真算例,对本文所提稳定性改善方法的有效性进行了验证。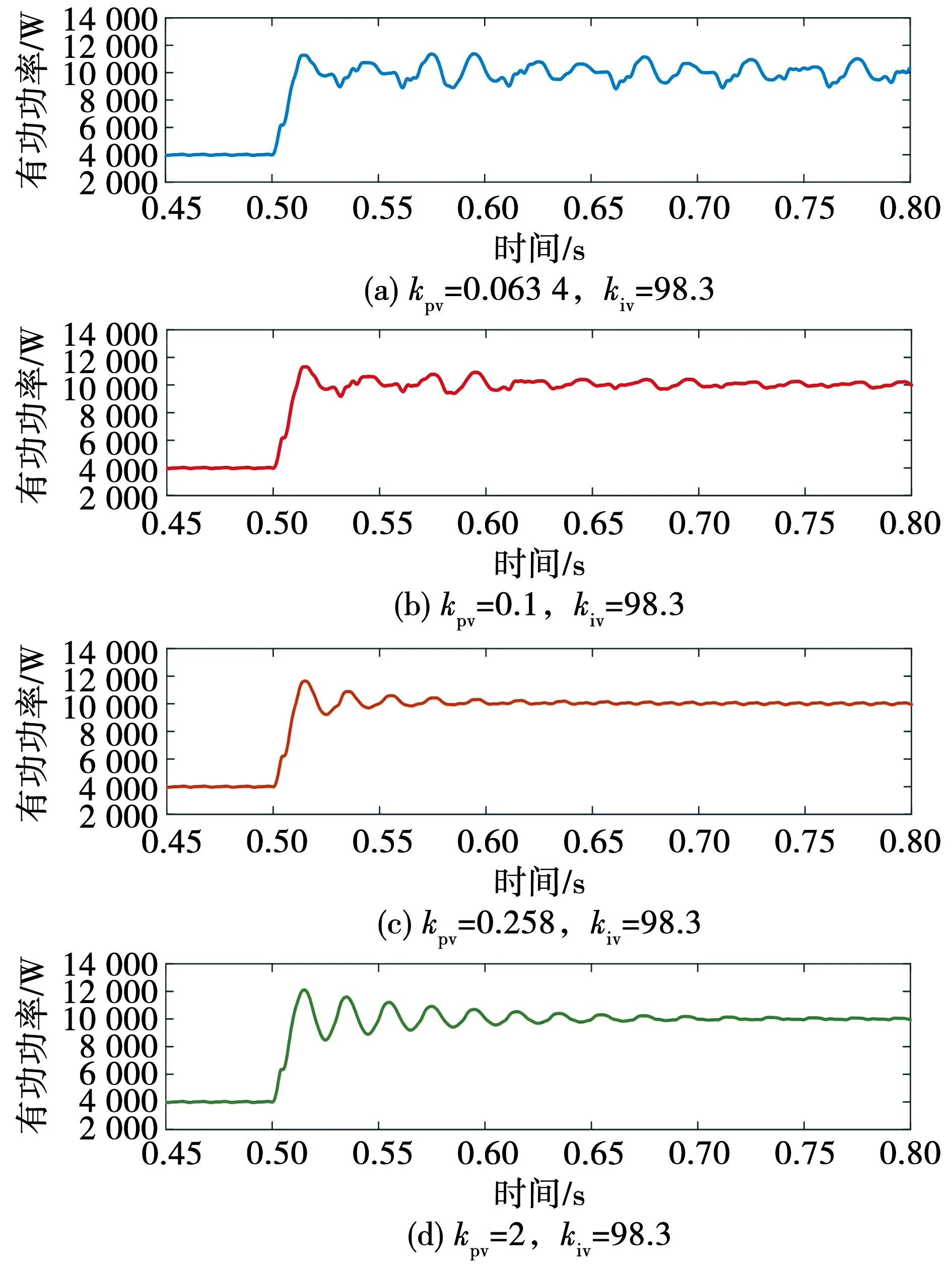
3 级联系统稳定性改善方法
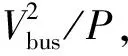
4 结 论
