高压电缆热机械效应分析与弧幅滑移量计算研究
2024-01-18倪一铭马宏忠段大卫薛健侗王健迮恒鹏万可力
倪一铭, 马宏忠, 段大卫, 薛健侗, 王健, 迮恒鹏, 万可力
(河海大学 能源与电气学院,江苏 南京 211100)
0 引 言
随着“双碳”政策的实施,高压电缆的建设快速发展,在城市输电设备中占据了重要地位。为了减少热机械应力的影响,大多数高压电缆采用蛇形敷设的方式[1],该方式在一定程度上可以减少热机械应力的影响。但由于弧幅滑移量参数选择不当或弧幅打弯半径缺少有效的标准等原因,蛇形敷设下的高压电缆表现出显著的热机械效应问题[2],例如绝缘层击穿、绝缘材料老化变质、接头破损等故障[3-4]。统计数据表明,2016~2021年,由于热机械效应导致的高压电缆故障约占总故障数量的60%。事后故障分析表明:高压电缆的热机械应力具有作用区域广、隐蔽性强、故障后果严重等特点[5-9]。
针对高压电缆的热机械效应,目前的研究集中在电缆材料的电气特性、物理场仿真等方面。文献[10]与文献[11]等研究了电缆在应力作用下绝缘层的性能,得出了绝缘性能与温度场、电场数值呈负相关的结论;文献[12]等通过高压XLPE电缆的热老化实验,研究了不同时间下的热机械振动产生的应力对绝缘层的损伤情况,得出了热机械振动会加速XLPE绝缘层老化的结论;文献[13]和文献[14]等通过建立电-热耦合模型,对故障电缆接头处的电场、温度场、应力场进行研究,分析了电缆接头处的物理场与接头结构损伤机理。综上,现阶段的研究集中于电缆热机械应力的宏观分析、绝缘层局部微观结构损伤、电缆及其接头物理场仿真等方面,在热机械效应下高压电缆应变的具体情况研究和能够用于实际工程敷设的参数计算方法等方面仍处于空白阶段。
本文首先分析高压电缆热机械效应与热机械应力机理,提出高压电缆应变计算方法和基于悬链线方程的弧幅滑移量计算方法;同时针对电压应变片的参数转化计算,提出一种基于直流电桥的电压应变片应变计算方法;其次采用有限元软件对高压单芯交流XLPE电缆进行建模,对热机械效应下温度场、应力和应变、弧幅滑移量进行仿真分析;再次通过高压电缆应变试验对其径向应变进行研究,验证应变计算方法的有效性,且热机械应力会使内部结构发生严重相互挤压;最后通过弧幅滑移量测量试验验证弧幅滑移量计算的结果,以试验测量值为基准,将新方法计算结果与有限元仿真结果、《城市电力电缆线路设计技术规定》(下文简称《规定》)计算结果进行对比分析,证明弧幅滑移量计算方法的准确性,为高压电缆敷设工程应用提供理论与数据支撑。
1 高压电缆热机械应力计算
常见的高压单芯交流XLPE电缆由内到外依次为导体、导体屏蔽、绝缘层、绝缘屏蔽、缓冲层、金属护层、电缆沥青和外护层组成[15],具体的截面示意图如图1所示。
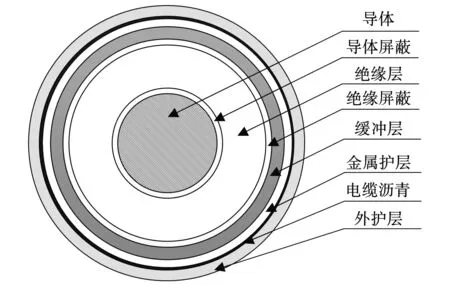
图1 高压电缆截面图Fig.1 High-voltage cable cross section
运行中的高压电缆由于内部材料性质不同,在负荷电流和环境温度的影响下,电缆会热胀冷缩产生热机械应力,使内部材料发生应变,称为热机械效应。考虑到高压电缆中导体、金属护层的密度、硬度远大于绝缘层等非金属材料,绝缘层等非金属部分材质产生的热机械应力可忽略不计[16],故重点研究导体、金属护层在负荷电流和环境温度影响下产生的热机械应力。
1.1 导体的热机械应力计算
负荷电流变化产生的导体热机械应力为
σC1=αCΔθC1ECAC。
(1)
式中:αC为导体的线膨胀系数,℃-1;ΔθC1为高压电缆正常运行时,导体的实际最高温度相对于当时环境温度的温升,℃;EC为导体的等值弹性模量,N/m2;AC为导体的横截面积,m2。
环境温度变化产生的导体热机械应力为
σC2=αCΔθC2ECAC。
(2)
式中:ΔθC2为高压电缆正常运行时,导体额定最高温度相对于当时环境温度的温升,℃;其余符号意义与式(1)中相同。
1.2 金属护层的热机械应力计算
负荷电流变化产生的金属护层热机械应力为
σM1=αMΔθM1EMAM。
(3)
式中:σM为金属护层的线膨胀系数,℃-1;ΔθM1为高压电缆正常运行时,金属护层的实际最高温度相对于当时环境温度的温升,℃;EM为金属护层的等值弹性模量,N/m2;AM为金属护层的横截面积,m2。
环境温度变化产生的金属护层热机械应力为
σM2=αMΔθM2EMAM。
(4)
式中:ΔθM2为高压电缆正常运行时,金属护层额定最高温度相对于当时环境温度的温升,℃;其余符号意义与式(3)中相同。
因此,高压电缆的热机械应力为
(5)
2 高压电缆应变计算
测量应变是将应变片直接与被测物体接触,根据应变片的电阻-应变效应以及相关计算公式推出物体的应变值。但现有公式在计算应变片面积变化时采用的是经验值估算[17],存在较大的估计误差。
针对现有方法的不足和高压电缆热机械效应中产生的应变,结合式(5)热机械应力的计算方法,提出一种基于直流电桥的电压应变片应变计算方法。
2.1 基于广义胡克定律的高压电缆应变计算
高压电缆内部各层结构可视为连续均匀的固体,且满足各向同性的假设条件[18]。根据广义胡克定律[19],各向同性材料的应变分量与应力分量之间满足方程:
(6)
(7)
(8)
式(6)~式(8)中:εx,εy,εz为线应变分量;E为等值弹性模量,N/m2;μ为泊松比;σx,σy,σz为正应力分量;τxy,τyz,τxz为切应力分量;γxy,γyz,γxz为切应变分量;G为切变模量,N/m2。
高压电缆产生的热机械应力在同一平面内,切应力分量为零[20],即τxy=τyz=τxz=0,故切应变分量为零。高压电缆由于温度升高产生应变,但高压电缆需满足安全运行要求,故应变不能无休止发生。考虑到高压电缆内部各结构间相互紧密约束,此时的应变量为
(9)
式中:α为外护层的线膨胀系数,℃-1;Δθ为高压电缆正常运行时,外护层的最高温度相对于当时环境温度的温升,℃。
2.2 基于直流电桥的电压应变片应变计算
直流电桥测量应变电路图如图2所示。当电压应变片发生如图3所示应变时,其电阻值会发生改变,此时该电桥的电压差值为
(10)
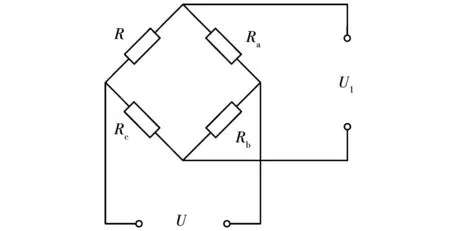
图2 直流电桥测量应变电路图Fig.2 Schematic of strain measurement based on DC bridge
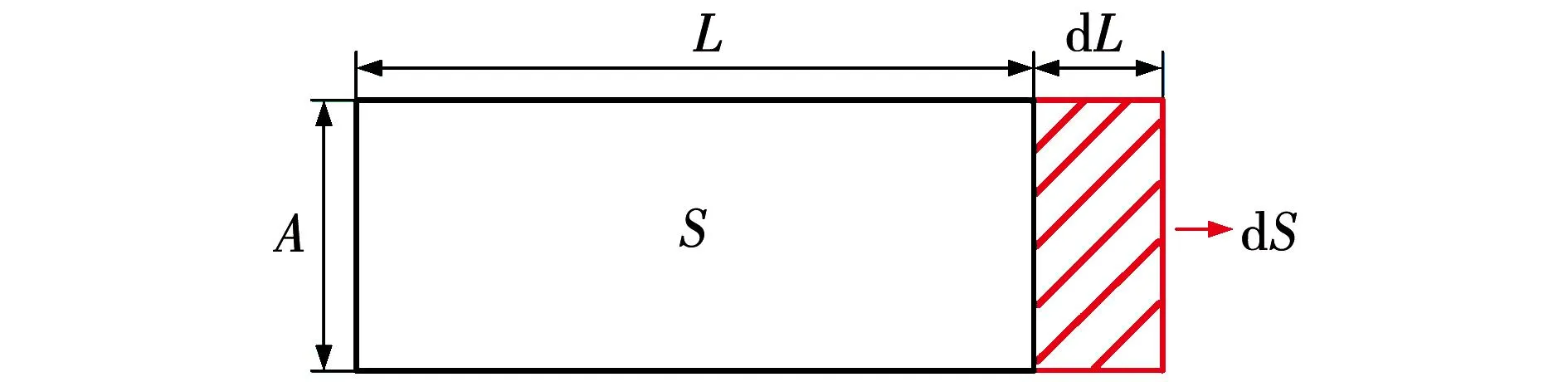
图3 应变片发生应变示意图Fig.3 Diagram of strain generation in strain gauges
式中:ΔU1为电压差值,V;R为应变片电阻,Ω;ΔR为应变片电阻的变化值,Ω;Ra、Rb、Rc为外接电阻,Ω;U为外接电源,V。
应变片电阻的计算公式为
(11)
式中:ρ为电阻率,Ω·mm;L为应变片长度,mm;S为应变片的面积,mm2。
式(11)两边同时取对数并微分:
(12)
式中dL/L为应变片长度的相对变化,可用应变ε表示,即ε=dL/L。
dS/S为应变片截面积的相对变化,即
(13)
式中μDMS为应变片的泊松比。
应变片的电阻率在测量过程中基本保持不变,即dρ/ρ=0。根据式(12)、式(13)可得,应变片的应变ε与电阻变化值ΔR近似满足:
ΔR≈dR=(1-μDMS)εR。
(14)
根据式(10)可求得ΔR,代入式(15)中即可求得应变:
(15)
3 高压电缆弧幅滑移量计算
蛇形敷设下的高压电缆在选择敷设参数时须考虑蛇形弧幅的滑移量,《规定》中提供了电缆的蛇形弧幅滑移量n的计算公式[21]:
(16)
式中:B为蛇形弧幅,mm;l为蛇形弧幅的水平长度,mm;m为电缆的热伸缩量,mm。
式(16)计算时需要已知电缆热伸缩量m,现有的测量仪器无法精确测出m的数值,且热伸缩量m涉及到摩擦系数,该系数是通过经验值进行估计,导致滑移量n的计算误差较大。针对现有计算方法的不足,提出基于悬链线方程的高压电缆弧幅滑移量的新计算方法。
3.1 悬链线方程
悬链线是一种常见的曲线,其物理意义为同一平面内,固定在水平两点间且受重力作用自然下垂的链条的形状[22],例如悬索桥等。以悬链线弧幅最低点为原点,建立如图4所示的平面直角坐标系,故可将悬链线方程设为y=f(x),固定悬链线的两点分别为点A和点B;设点D(x,y)为悬链线上任意一点,该点的切线方向与水平方向的夹角设为φ。
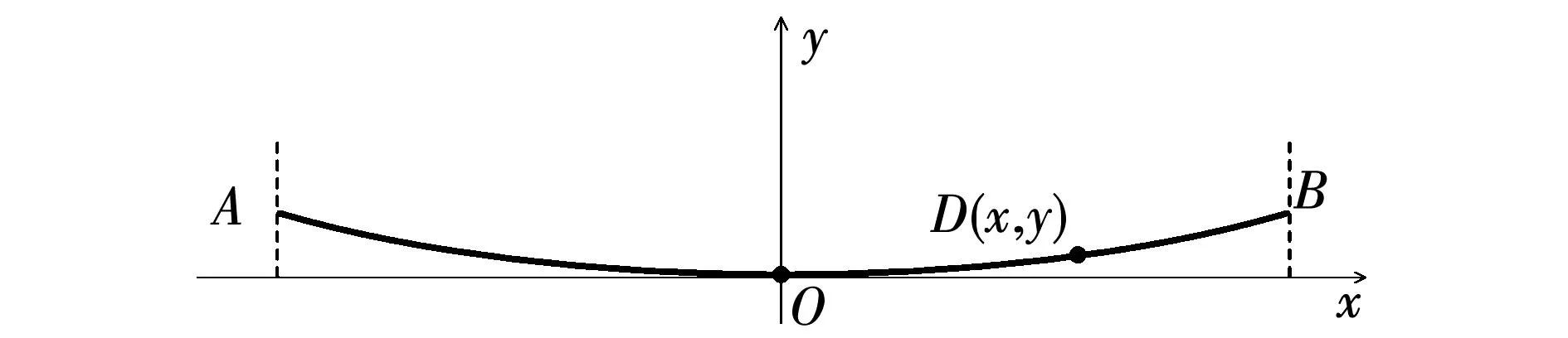
图4 悬链线Fig.4 Catenary
对点D进行受力分析可知,点D受到沿其切线方向的拉力F,铅锤方向上的重力G以及水平向左的拉力T,如图5所示。
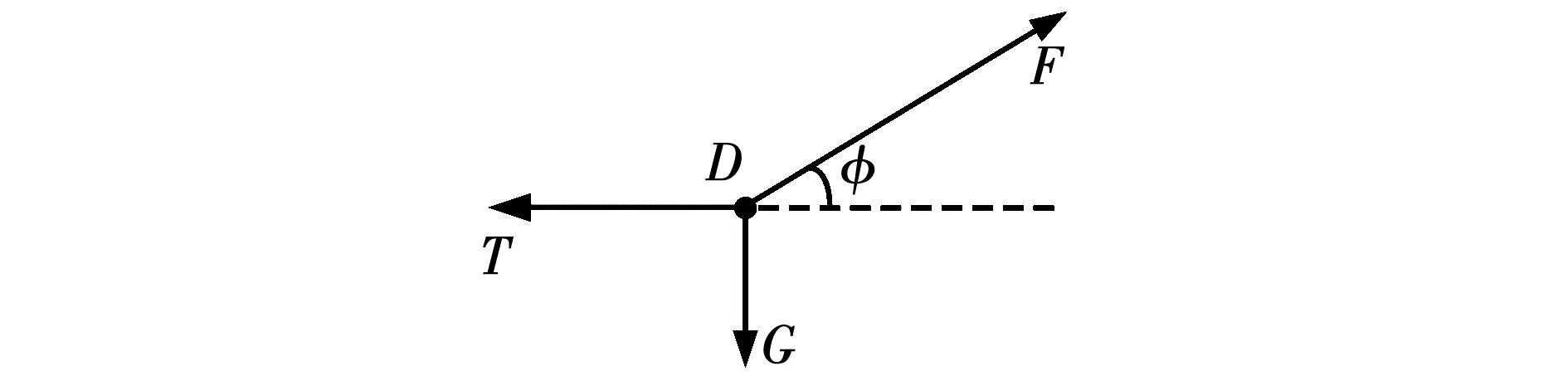
图5 受力分析Fig.5 Analysis of forces
由受力分析可知:
(17)
重力G和拉力T可表示为:
(18)
(19)
式中:k为链的自重比载,N/m·mm2;S为链的截面积,mm2;Lx为点O与点D间的弧长,m;ψ0为链中的压强,MPa;M0为每公里链的质量,kg/km。
任意点D的斜率可由tanφ表示,结合式(16)得
(20)
式(20)两边取微分可得
(21)
式(21)两边整理并积分可得
(22)
由双曲函数积分公式并结合式(22)化简,代入初始条件x=0,y=0时,tanφ= 0可得悬链线方程为
(23)
3.2 基于悬链线方程的高压电缆弧幅滑移量计算
蛇形敷设下的高压电缆两端受到夹具的固定,弧幅自然下垂,故可近似等效为一条悬链线,如图6所示。在热机械应力的作用下,蛇形弧幅会向下发生一定量的滑移。由于蛇形敷设下的高压电缆可看作是水平对称的,高压电缆的蛇形弧幅滑移即为图中的点O处产生的滑移量n。

图6 蛇形敷设的高压电缆Fig.6 Snake laying high-voltage cable
计算高压电缆的滑移量时,悬链线方程中的压强ψ0(MPa)可用式(24)的热机械应力σ(N)计算得到:
(24)
为计算点O处的滑移量,将式(24)代入式(23)并展开为x=0的麦克劳林级数:
(25)
考虑到实际蛇形敷设下的高压电缆夹具处电缆存在一定的弯曲半径且其水平长度远大于弧幅(d/l≤0.1),可略去式(25)中的高次项式[23],其精度可以满足敷设工程的需要,即
(26)
将x=l/2代入上式,可得高压电缆蛇形弧幅滑移量
(27)
式中l为高压电缆的水平长度,单位m。
4 高压电缆有限元仿真分析
4.1 高压电缆有限元建模仿真
高压电缆中的导体屏蔽、绝缘屏蔽以及电缆沥青厚度相对较小且材质与相邻层近似,考虑到建模中有限元网格划分,故将导体屏蔽、绝缘屏蔽与绝缘层合并,电缆沥青与外护层合并[24],故内部具体结构由内到外依次为:导体、绝缘层、缓冲层、金属护层、外护层,各结构具体参数如表1所示。在COMSOL Multiphysics中建立上述高压电缆的实物模型,相邻夹具之间的水平距离约为4 m,高压电缆弧幅约为0.20 m;在建模时高压电缆两端向外侧延伸1 cm并设置为固定约束,模拟高压电缆两端的夹具固定,如图7所示。
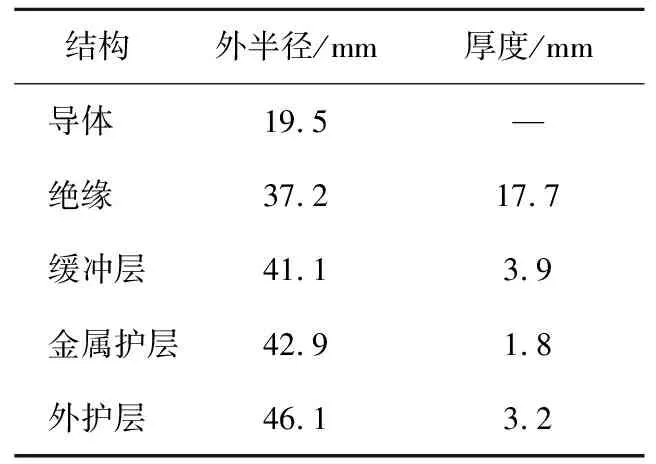
表1 电缆结构参数Table 1 Cable construction parameters
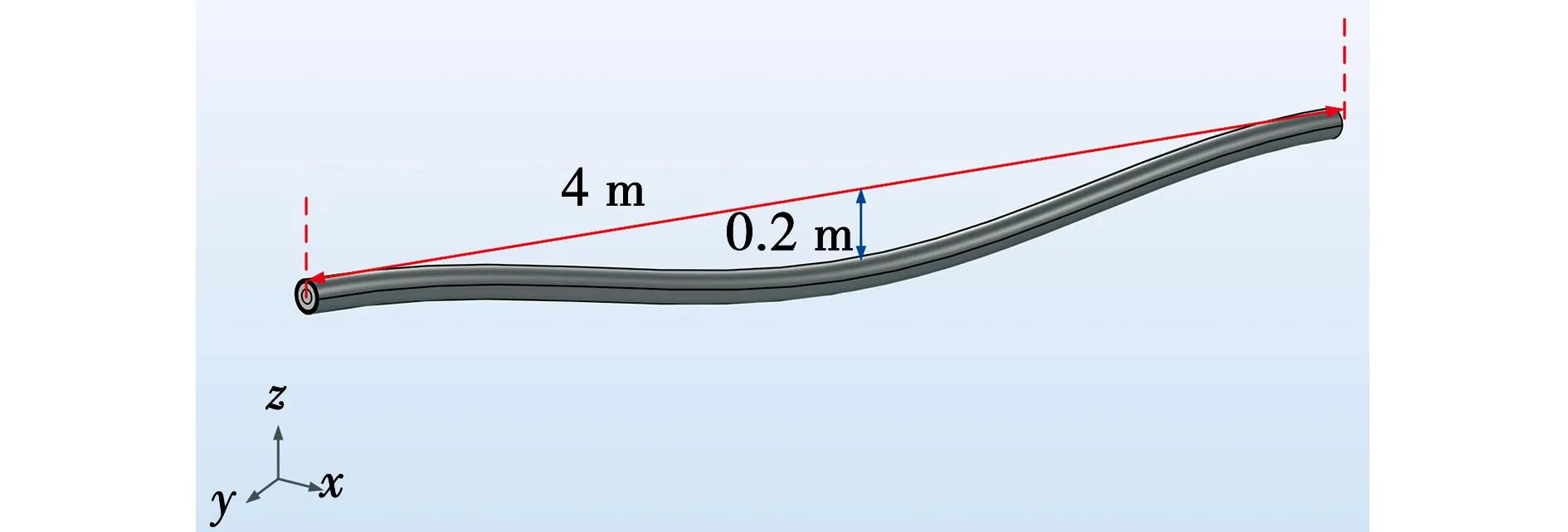
图7 有限元模型Fig.7 Finite element modelling
为了研究高压电缆的热机械效应与弧幅滑移量,模拟高压电缆在负荷电流下运行,但须确保导体的最高温度不超过90 ℃[25]。高压电缆产生的热量主要通过热传导方式传递到外护层表面[26],电缆外护层与外界换热主要通过热对流方式实现[27]。因此,在模型中设定边界条件:外护层与空气接触面传热系数10 W/(m2·K),外部温度与高压电缆初始温度均设置为293.15 K。
4.2 温度场仿真
模拟高压电缆实际运行后,高压电缆温度截面图和曲线图分别如图8、图9所示,其最高温度达到了68.1 ℃。由于导体、金属护层是高压电缆中的热源,金属材料具有良好的导热性,电缆温度在导体、金属护层区域无明显变化。高压电缆的整体温度随运行时间递增,绝缘层等非金属部分温度由内向外递减,近似呈线性减少趋势。

图8 高压电缆温度截面图Fig.8 High-voltage cable temperature cross section
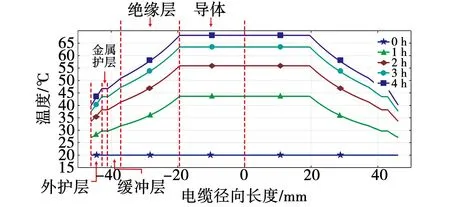
图9 不同运行时间下高压电缆温度图Fig.9 Temperature diagram for high-voltage cables at different operating times
4.3 应力与应变仿真
高压电缆中导体、金属护层产生的热机械应力远大于绝缘层等非金属部分产生的热机械应力如图10~图12所示。夹具处的热机械应力的最大值存在于金属护层与缓冲层的接触面,仿真中该接触面的压强已接近于金属护层材质铝的屈服强度最大值,金属护层可能会发生损坏。

图10 金属护层应力分布图Fig.10 Metal sheathing stress distribution diagram
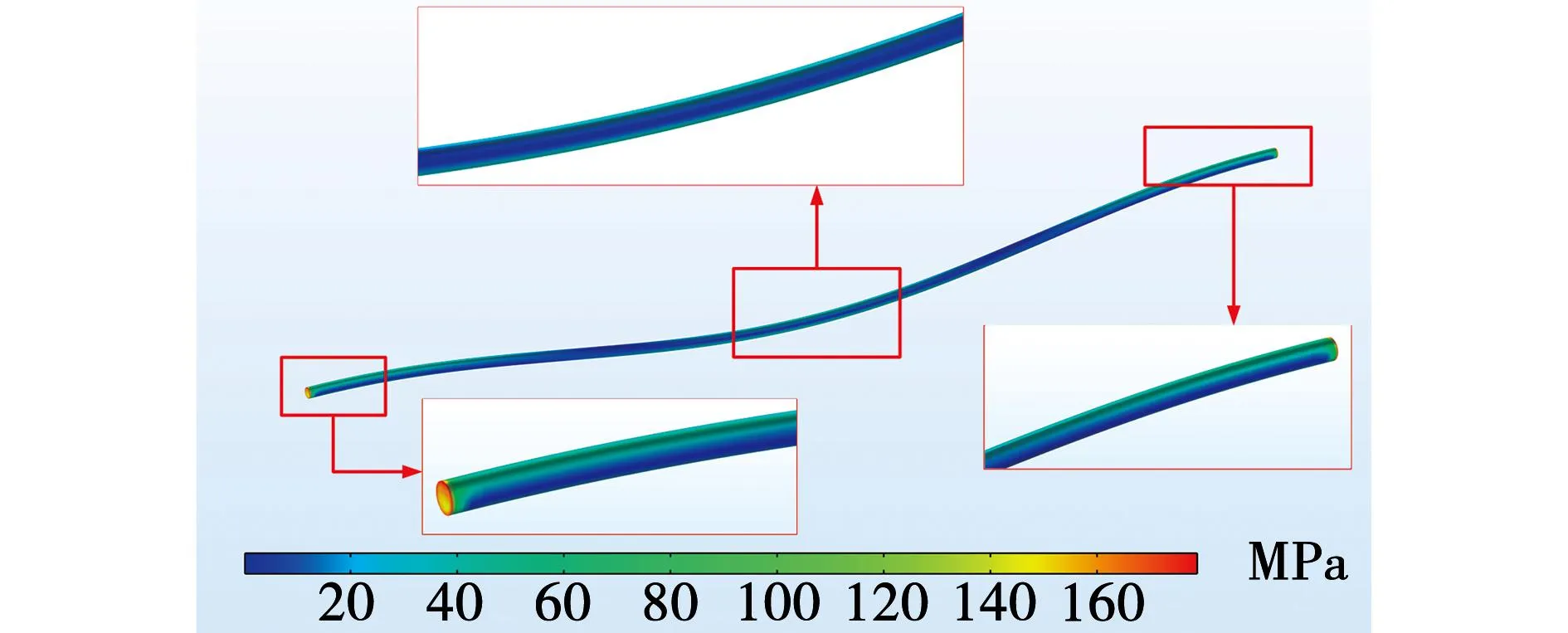
图11 导体应力分布图Fig.11 Conductor stress distribution diagram

图12 非金属部分应力分布图Fig.12 Stress distribution diagrams for non-metallic parts
高压电缆在热机械应力下会产生应变,选取高压电缆的应变截面图如图13所示。绝缘层、外护层会发生较为明显的热膨胀,其中绝缘层受热膨胀约1.4%,外护层受热膨胀约0.6%。导体产生的热量和热机械应力直接施加在导体与绝缘层的接触面上,在两者的共同作用下,该接触面的应变值最大。在这种情况下运行,绝缘层将加速老化,长时间后其内部结构将造成不可逆的热疲劳拉伸,存在安全隐患。

图13 应变截面图Fig.13 Strain section diagram
4.4 弧幅滑移仿真
高压电缆在夹具固定作用下,自身达到一种受力平衡的状态。但热机械应力打破了该平衡状态,高压电缆在热机械应力下产生滑移,滑移较大的部分集中于蛇形弧幅,夹具处的电缆几乎不发生滑移,如图14所示。
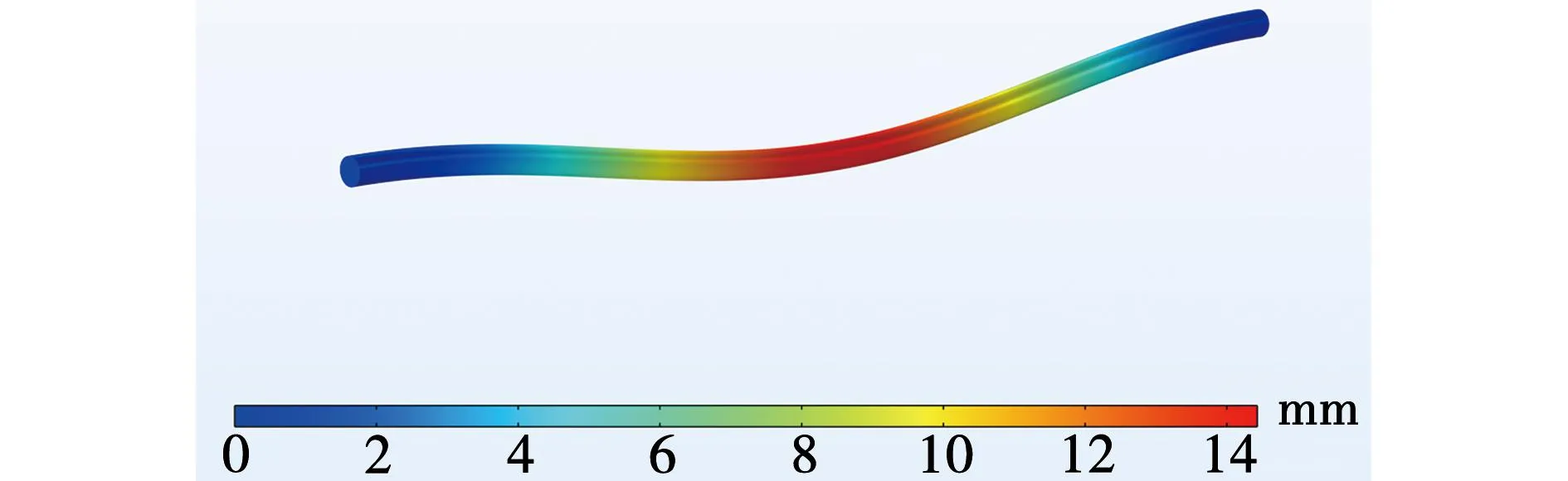
图14 电缆滑移分布图Fig.14 Cable slip distribution map
不同运行时间下电缆全长的滑移分布曲线如图15所示,所有时间下的滑移分布曲线均关于x=0对称且最大值出现在该处,故可判断最大滑移发生在蛇形弧幅的最低点。
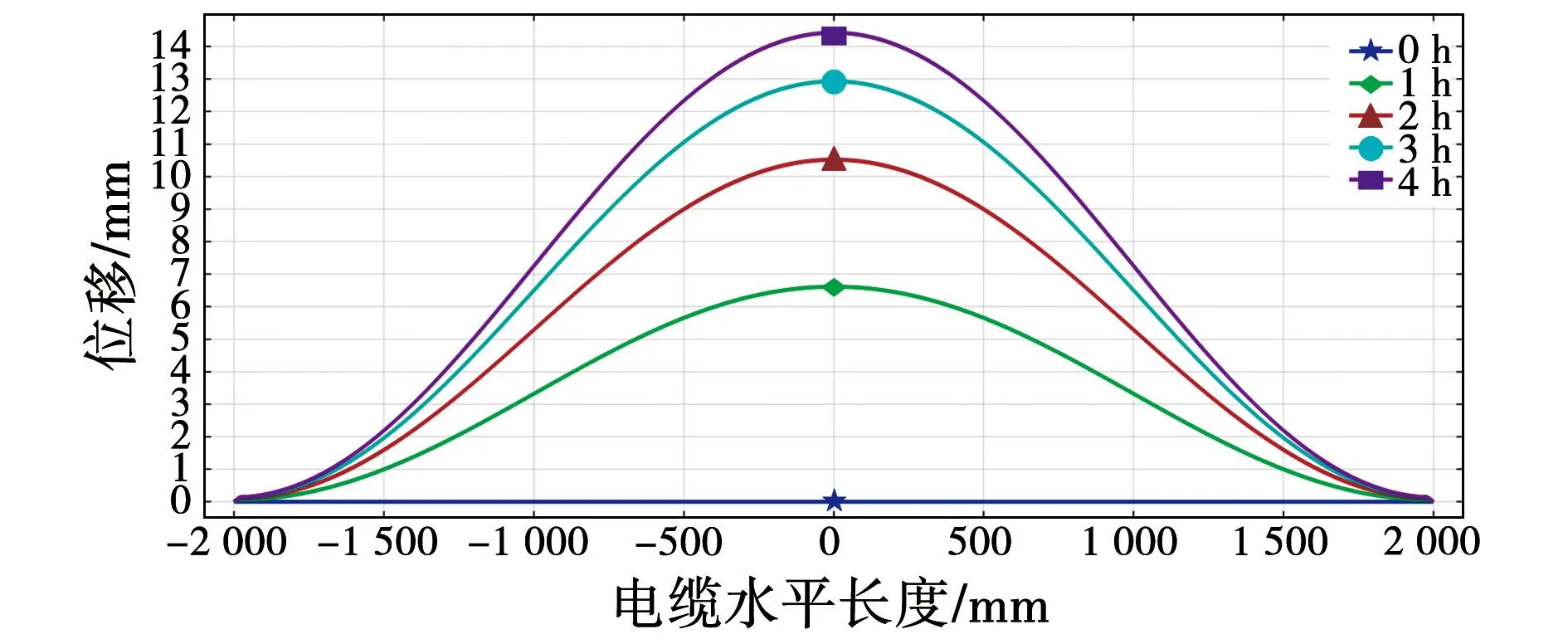
图15 不同运行时间下电缆全长滑移分布图Fig.15 Slip distribution of the full length of the cable at different operating times
5 试验验证与分析
国内某市高压单芯交流XLPE电缆实际敷设现场如图16所示。高压电缆敷设于专用的电缆隧道中,夹具之间水平距离为4.04 m,高压电缆处于自然下垂状态,初始弧幅最大处约为0.18 m。该隧道中的电缆规格为1 200 mm2的单芯电缆,具体结构参数同表1。为分析高压电缆热机械效应下电缆产生的应变与弧幅滑移量,在高压电缆敷设现场进行应变试验与弧幅滑移量测量试验。

图16 高压电缆敷设现场Fig.16 High-voltage cables laying site
5.1 应变试验与分析
高压电缆的应变在负荷电流较小时不易测量,为了确保试验分析的准确性,本次试验选择在日负荷电流较大的时段研究应变情况。当地的供电公司后台长期监测0~24时运行负荷电流的数值,日负荷电流较大时段约为10~14时,平均值约为550 A,故选取该时段进行应变试验。
在不改变高压电缆任何敷设参数的情况下,选取高压电缆蛇形弧幅段外表面上的某个位置进行应变测量。如图17所示,在该位置上布置四个应变片,该应变片可将应变量转化为电压值输出;应变量与始末输出电压差值成正比,可通过式(15)计算出应变值,并可判断高压电缆内部结构的应变状况,试验示意图如图18所示,试验现场如图19所示。
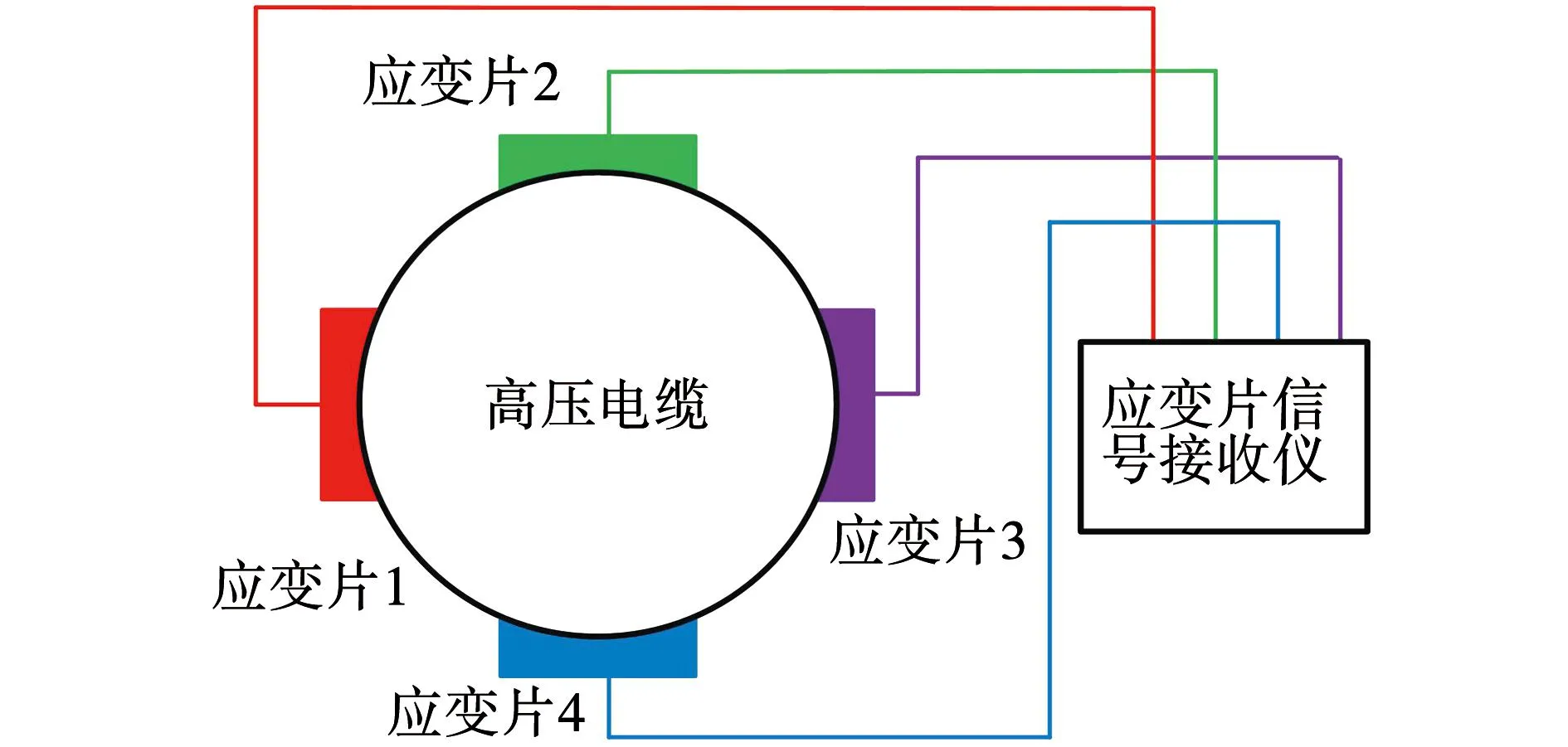
图17 应变片布置示意图Fig.17 Strain gauge arrangement diagram
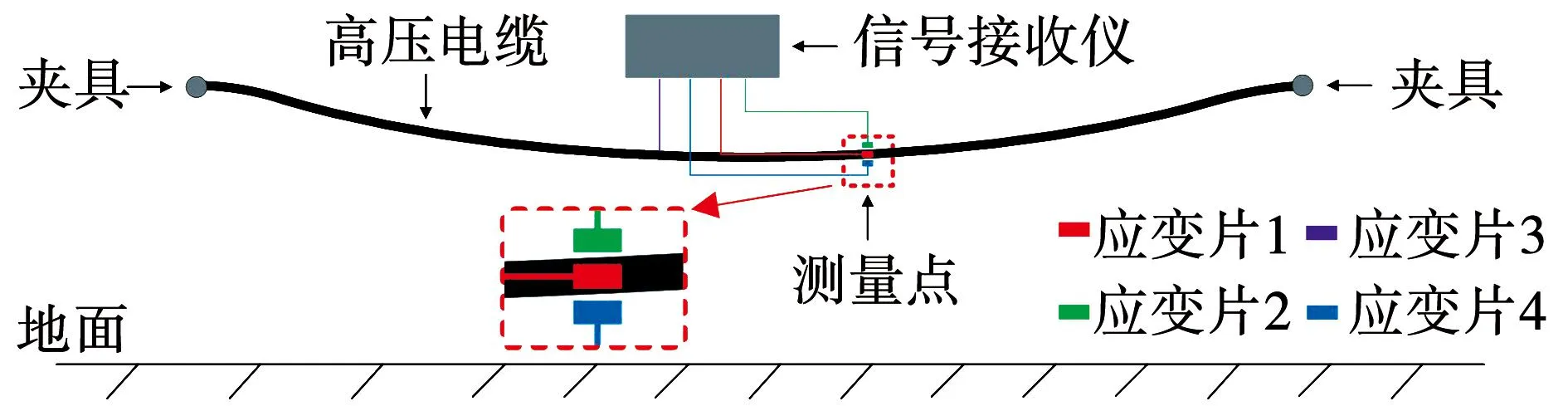
图18 试验示意图Fig.18 Schematic diagram of the experiment

图19 试验现场图Fig.19 Experimental site plan
试验开始测量时间选择为9时55分,结束测量时间为14时05分,当天0~24时的负荷电流如图20所示,试验测量时段的平均电流为551.69 A。不同位置上的应变片都要达到电压平衡的状态,所以应变信号接收仪中的调零电位器自动设置的初始输出电压值不同。测量结束后导出接收仪中记录的输出电压值,经小波降噪后得到输出电压波形如图21所示。
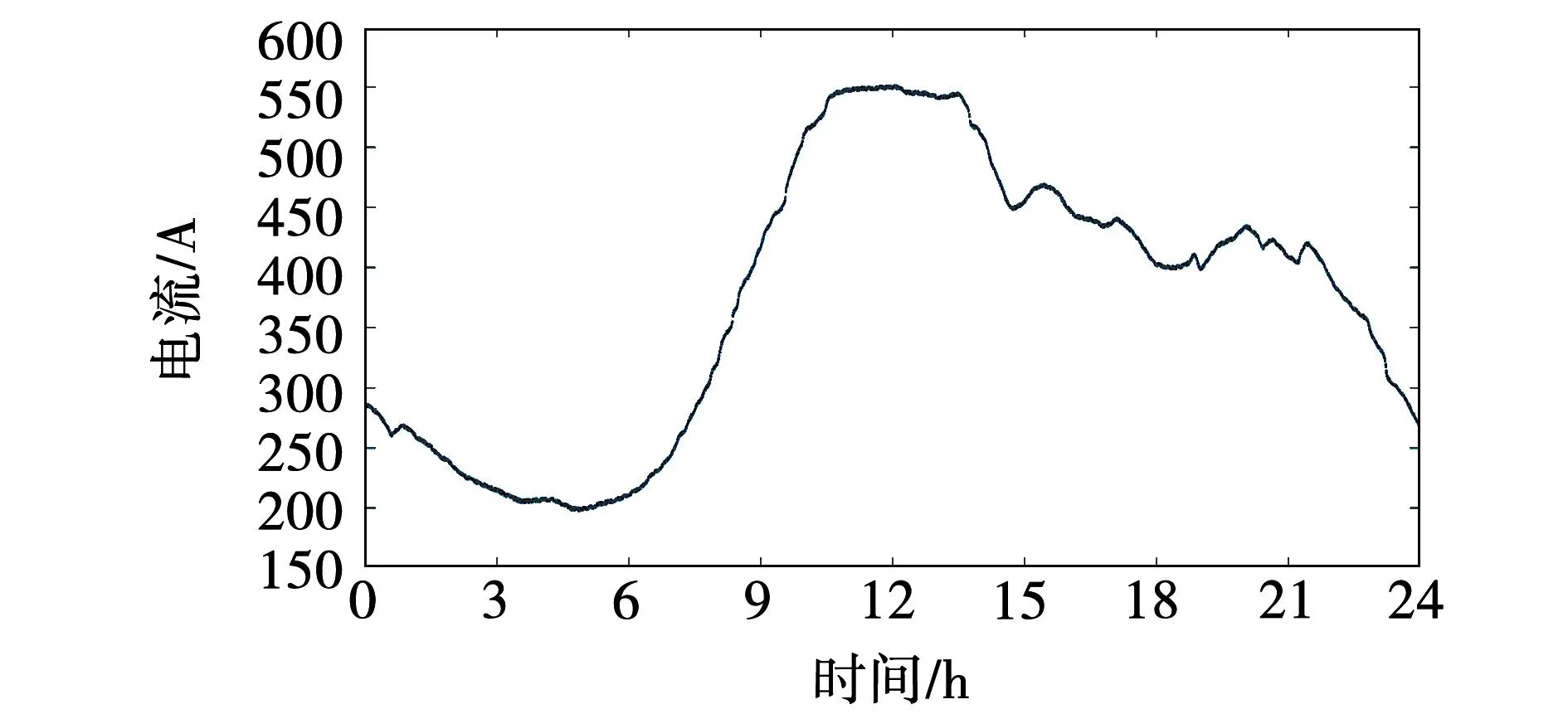
图20 当天0~24时的负荷电流Fig.20 Load current from 0 to 24 hours of the day
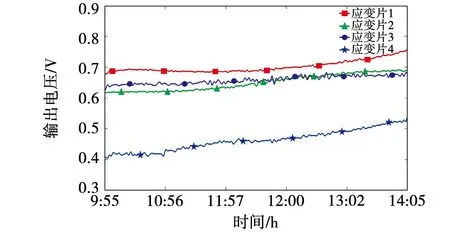
图21 应变片输出电压Fig.21 Output voltage of strain gauges
与图13仿真得到的应变图对比,在理想化的运行条件下,高压电缆运行会发生热膨胀,其内部各层均产生了应变。但试验过程中存在负荷波动、温度变化等因素,根据应变测量结果可以看出:高压电缆沿径向发生了不同程度的热膨胀,导致了内部各层发生了不同的应变。
通过试验分析和数据计算,各应变片的应变的数据如表2、3所示。根据式(15)计算得到应变片1~4的应变量为1.84、1.19、1.12、2.16 mm,试验中应变片4的位置发生了较大的应变。

表2 应变片数据Table 2 Strain gauge data 单位:V

表3 测量与计算数据Table 3 Measurement and calculation data 单位:mm
式(9)基于广义胡克定律的高压电缆应变计算结果为2.33 mm,结合应变片1和4产生的应变量相近,且两者明显大于应变片2和3的结果,可以推出由于高压电缆内部材料属性不同,导体、金属护层在热机械应力作用下在径向平面向左下方发生了相对偏移,即应变片1和4的中间位置,该位置存在应变量最大值,如图22所示。
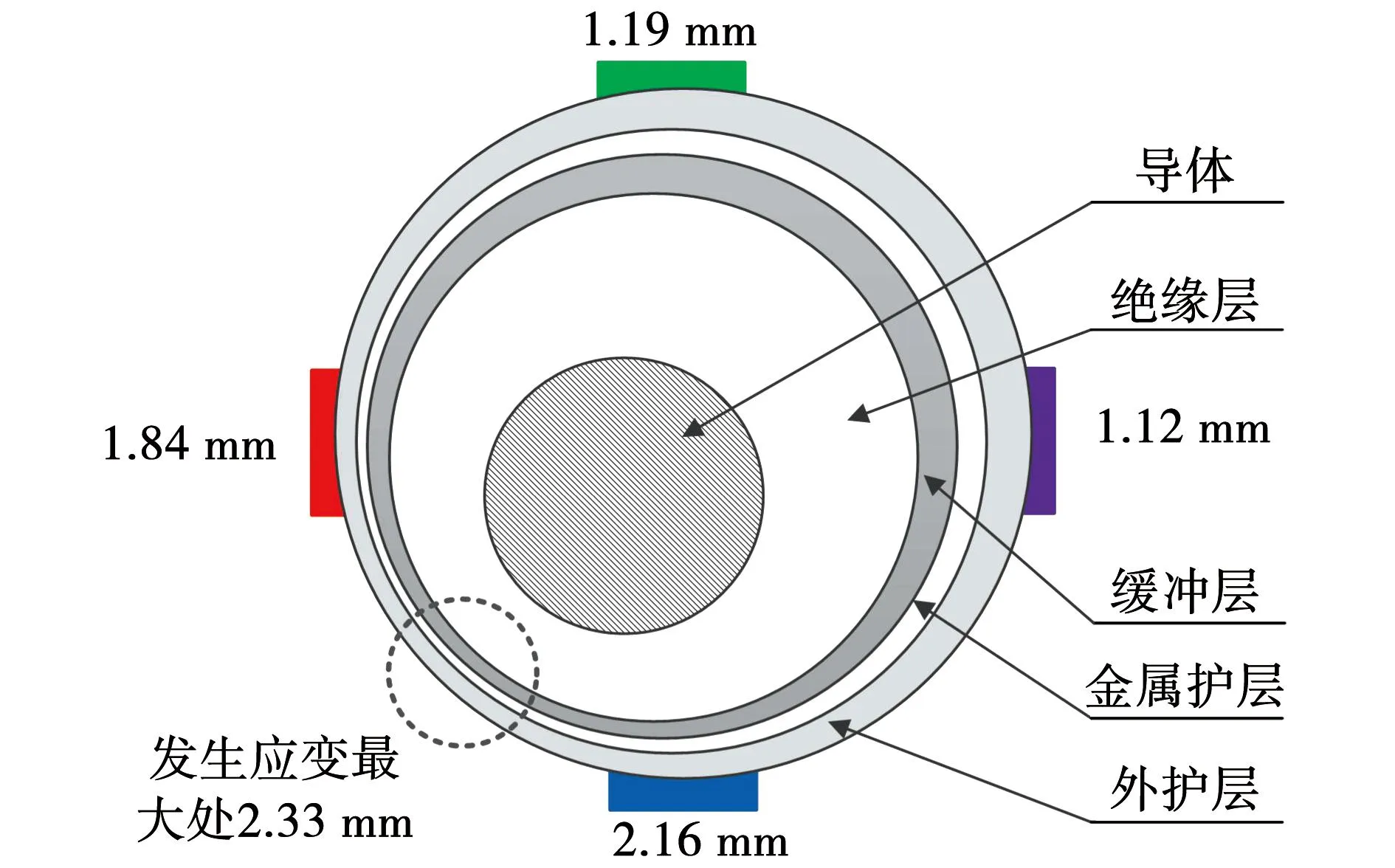
图22 内部结构偏移图Fig.22 Internal structure offset diagram
高压电缆是一个密封的整体,导体、金属护层产生的热机械应力直接作用于绝缘层、缓冲层、外护层产生应变,然后被外护层上布置的应变片测量得到。该试验结果表明:在热机械效应中,热机械应力会使高压电缆发生不均匀的应变,电缆内部的金属部分会严重向下挤压非金属部分。热机械应力长时间作用于绝缘层上,会造成绝缘的热拉伸、热老化等现象[4],导致分子键的断裂、绝缘击穿电压降低[12],可能造成高压电缆的运行事故。
5.2 弧幅滑移量测量试验与分析
本试验采用2个激光测距传感器,测量高压电缆产生的滑移量。通过测量不同时刻高压电缆蛇形弧幅距离传感器的高度可以得到滑移量的具体数值,试验示意图如图23所示。本试验采用的激光测距传感器测量精度较高,需在地面上架设一个辅助支架,从而将测量距离控制在传感器量程范围内,试验现场如图24所示。

图23 试验示意图Fig.23 Schematic diagram of the experiment

图24 试验现场图Fig.24 Experimental site plan
激光测距传感器测量了当天0~24时的高压电缆蛇形弧幅距离传感器的高度H的数值,如图25所示。设前一天运行结束24 h的H值为初始高度H0,经测量初始高度H0为17.90 cm。结合图17分析,0~7 h处于谷时用电阶段,负荷电流较小,此时高压电缆中产生的热量会相较于前一天晚上峰时用电时产生的热量大幅减少,电缆会因此向上“收缩”。随着8 h开始负荷电流的增大,H值开始减小,即蛇形弧幅开始向下产生滑移;在负荷电流增幅较大的7时30分~13时19分,H值减幅较大,并在15时42分时出现最小值Hmin为16.49 cm,即相对于初始高度H0滑移了1.41 cm。表4提供了部分时间点的负荷电流数与H值,表中滑移数值为正表示向下滑移,数值为负表示向上滑移。
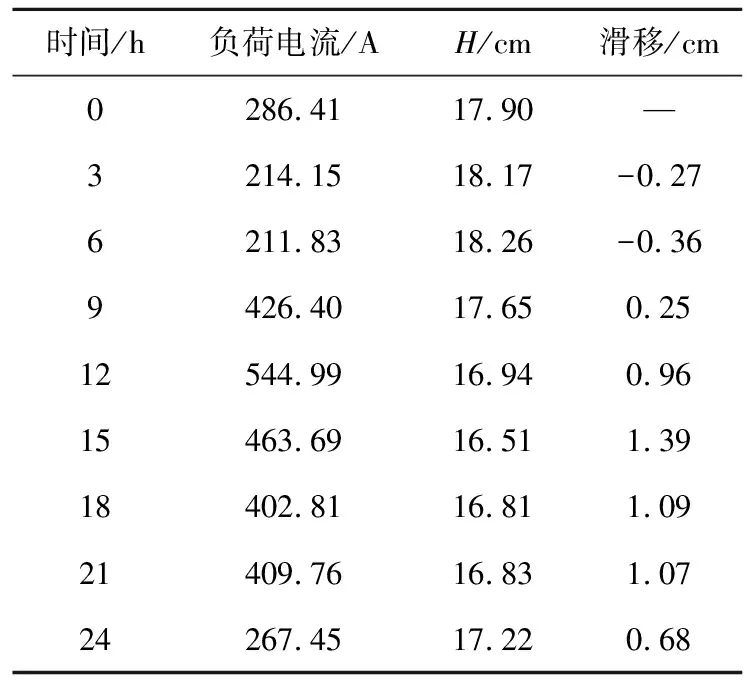
表4 部分时间点的负荷电流数与H值
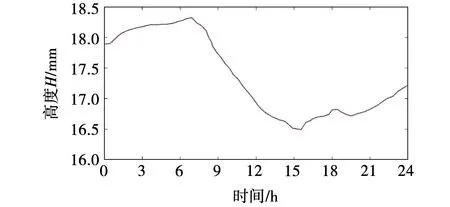
图25 当天0~24时的高度Fig.23 Height of the day from 0 to 24 hours
从上述试验过程中测得的数据可以得出,高压电缆在运行过程中产生的热机械效应会使高压电缆发生滑移,如图26所示,可以得出以下结论:负荷电流越大,产生的热机械效应越大,高压电缆在热机械应力作用下产生向下滑移,滑移量的大小会随着负荷电流的变化趋势产生相同的变化;瞬时的负荷电流波动不能产生明显的滑移,只有负荷电流大幅增大且持续一段时间后才发生滑移,说明高压电缆存在热惯性与机械惯性,热机械效应不是一个瞬时的过程,会随运行时间持续“叠加”。
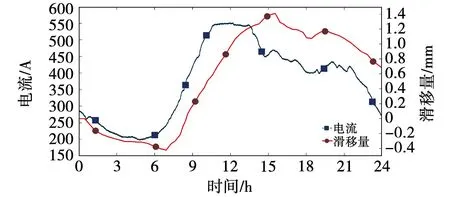
图26 时间-负荷电流-滑移图Fig.26 Time-load current-slip diagram
根据《规定》中的相关滑移量计算公式(16),计算得到弧幅滑移量为11.21 mm;用有限元软件对敷设隧道中的高压电缆进行1∶1建模仿真计算,其弧幅滑移量为14.43 mm,如图27所示。
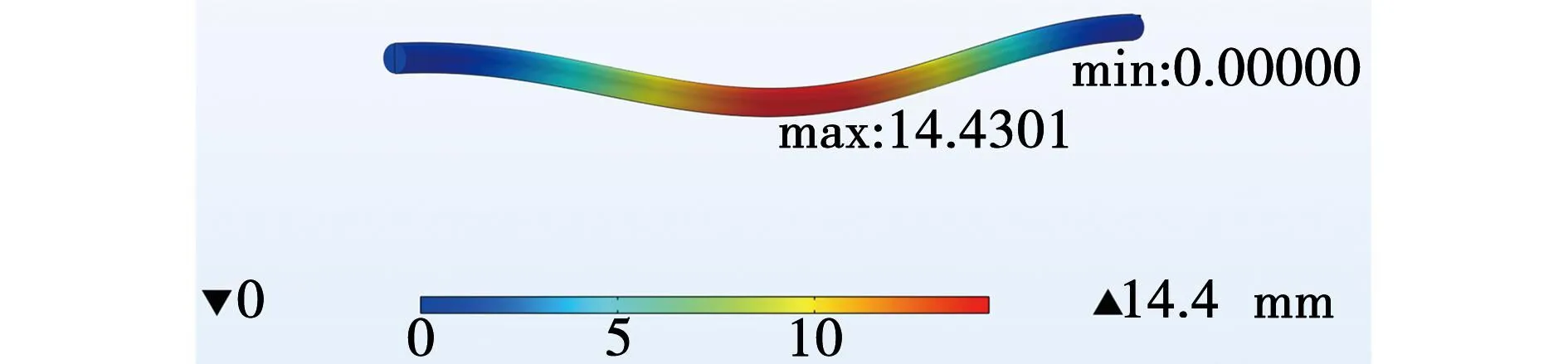
图27 有限元仿真结果Fig.27 Finite element simulation results
针对第3节中计算高压电缆弧幅滑移量所需参数如表5和表6所示,当时隧道内的温度约为21.2 ℃,该电缆的自重比载为0.38 N/m·mm2。将参数代入式(26),可得该电缆在热机械应力下产生的弧幅滑移理论计算值为14.26 mm。

表5 导体参数Table 5 Conductor parameters

表6 金属护层参数Table 6 Metal sheathing parameters
表7列出了不同方法得到的高压电缆弧幅滑移计算结果,以试验测量数据为基准值进行对比误差分析:由于有限元仿真中,高压电缆中流过的负荷电流的无法模拟实际运行中电流的数值波动,故存在一定量的仿真误差;基于悬链线方程的高压电缆弧幅滑移量计算方法的相对误差小于《规定》中的相对误差,且计算结果符合有限元仿真结果与试验测量数据,证明了本文提出的弧幅滑移量计算方法是较为准确的。
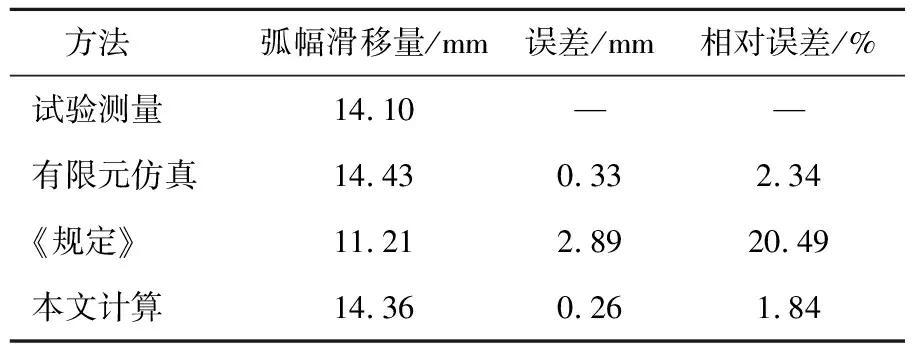
表7 不同计算方法及结果Table 7 Different calculation methods and results
6 总 结
本文对高压电缆的热机械效应进行研究,提出了热机械应力、应变和弧幅滑移量的计算方法,通过有限元仿真,分析了热机械应力下高压电缆的应变和弧幅滑移量,并通过现场试验验证了本文计算方法的有效性,总结如下:
1)基于广义胡克定律提出了一种适用于高压电缆热机械效应的最大应变计算方法,该应变计算方法符合高压电缆热机械效应的实际情况,且通过应变试验验证了本方法的可行性。
2)基于直流电桥的电压应变片应变计算方法详细分析了应变片的实际应变情况,对应变片面积的变化采用微分计算,该方法计算简便且具有良好的现场适用性,可用于其他电力设备的应变测量。
3)通过分析高压电缆径向平面的应变量,热机械效应下的导体和金属护层会严重向下挤压绝缘层、缓冲层、外护层,二者长期挤压会对高压电缆绝缘层、缓冲层、外护层产生不可逆的损伤。
4)基于悬链线方程的高压电缆弧幅滑移计算方法与有限元仿真、试验测量、《规定》进行结果对比分析,该方法符合实际运行情况且相对误差较小、计算便捷,为高压电缆的弧幅滑移量计算提供了理论支撑。此外滑移量也可作为高压电缆运行状态的监测量,可及时预防热机械效应下的潜在故障。
