基于UG和Ansys的塑料齿轮动态啮合分析

林梅彬

（福州职业技术学院 交通工程学院，福建 福州 350108）

齿轮传动系统常应用于车辆变速箱、工程机械等传动系统，是一种复杂的非线性系统，包含众多非线性因素，包括齿侧间隙、啮合刚度等[1].其中，以塑料材料为主的齿轮系统，由于具有质量轻、噪声低和成本低等优点，在汽车、家电和轻工业机械行业都得到了广泛应用.由于塑料齿轮的弹性模量和强度相比金属材料都低，因此传动系统采用塑料齿轮时，必须对塑料齿轮的动态啮合过程中的强度进行校核[2].齿轮系统的研究主要采用数学建模与仿真分析的方法，数学模型往往采用单自由度的模型[3]，塑料齿轮系统研究基于金属齿轮系统，一般也采用数学模型进行求解分析.多数学者以Matlab 作为研究工具，采用龙哥库塔法对齿轮系统动力学模型进行求解[4].随着计算机仿真技术的进步，对于齿轮系统的研究更多的采用动态分析方法.Anasys Workbench 作为大型通用的有限元仿真软件，已被广泛应用于动态系统的强度分析.云永琥等[5]利用仿真软件分析了不同载荷对塑料齿轮啮合传动的影响；谢卫兵[6]对比分析了塑料齿轮静态分析的有限元结果和试验结果，验证了仿真模型的正确性；周昊昊[7]对塑料齿轮进行了热-结构耦合分析，研究得出了不同载荷下的应力应变变化情况.以上研究中，学者们虽然采用了动态仿真技术分析得到了一些可靠的结论[8-11]，但在这些仿真分析中，特别是有限元的动态仿真中没有提及齿侧间隙参数.齿侧间隙是影响齿轮啮合传动的一个非常重要的非线性因素.齿轮啮合过程中，轮齿啮合的对数不断交替变化，齿侧间隙的大小将直接影响啮合周期内齿轮齿面接触的时间，进而影响啮合刚度的大小，对齿轮的动态啮合特性影响较大，包括轮齿受力情况、轮齿变形情况.

文中以塑料直齿轮作为研究对象，在UG中建立了考虑齿侧间隙的塑料齿轮系统三维模型，在Ansys Workbench 中设置合理的齿面摩擦系数和齿轮刚度，运用瞬态动力学仿真模块分析了塑料齿轮啮合中的应力分布和变形情况.

1 塑料齿轮动力学模型

建立单自由度的塑料齿轮系统动力学模型[12]如图1 所示.图中：T表示作用在齿轮上的扭矩；θ表示齿轮的扭转位移；R表示齿轮的基圆半径；I表示齿轮的转动惯量；e(t)为综合传递误差；km(t)为齿轮副的啮合刚度；cm为齿轮副的啮合阻尼；Ff为齿轮副的啮合摩擦力.

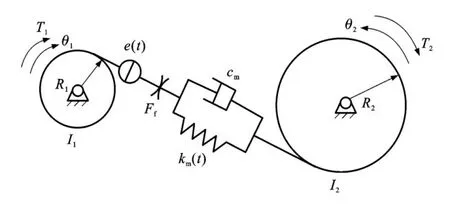
图1 单自由度齿轮系统模型

该系统模型的数学表达式为

式中：ζ为无量纲阻尼；ε为刚度波动系数；Fa为误差系数；Fem为无量纲扭矩；f(x)为间隙非线性函数，其表达式为

由间隙非线性函数表达式可知，齿侧间隙的大小会影响齿轮啮合接触状态，建模时要充分考虑模型的齿侧间隙，使得到的结果更符合实际情况.

2 模型建立

2.1 塑料齿轮三维模型的建立

文中应用UG 软件作为建模工具，采用软件自带的齿轮工具箱模块进行参数化建模.选用的塑料齿轮主要参数见表1.

表1 啮合齿轮参数表

需要注意的是，在UG中以啮合接触建立的塑料齿轮模型默认的齿侧间隙2b=0 mm.实际上，在齿轮啮合过程中，过小的齿侧间隙会加剧齿轮的损耗甚至出现卡死现象，故需要对齿轮模型的间隙进行调整，通过改变齿轮的中心距离改变齿侧间隙.将齿轮间隙2b调整为0.072 04 mm，调整后的齿轮模型如图2.

图2 含齿侧间隙的齿轮模型

2.2 塑料齿轮有限元模型的建立

通过有限元材料设置模块将塑料齿轮的材料设置为PA66.将塑料齿轮3D 模型通过UG 软件导入Ansys Workbench 中进行材料设置并进行网格划分，完成的有限元模型如图3 所示，网格划分的节点数量为107 361个，单元数量为21 800个.

图3 塑料齿轮有限元模型

主要材料属性：密度为1 140 kg·m-3；泊松比为0.41；弹性模量为1 480 MPa.

2.3 边界条件及载荷施加

为便于齿轮系统的动态啮合仿真分析，将主、被动齿轮的内圈进行body-ground转动副设定，如图4所示.文中不考虑传动轴、轴承支撑刚度和轴承阻尼的影响，将主动轮的转速设置为50 r·min-1，被动轮受到的负载扭矩设置为100 N·mm.将吃面摩擦系数f设置为0.1，啮合阻尼系数ξ设置为0.15.接触方式选择faceto-face，保证接触条件设置正确.为了便于观察齿轮动态啮合的变化情况，将处理设置的变形量开关设置为大变形量.

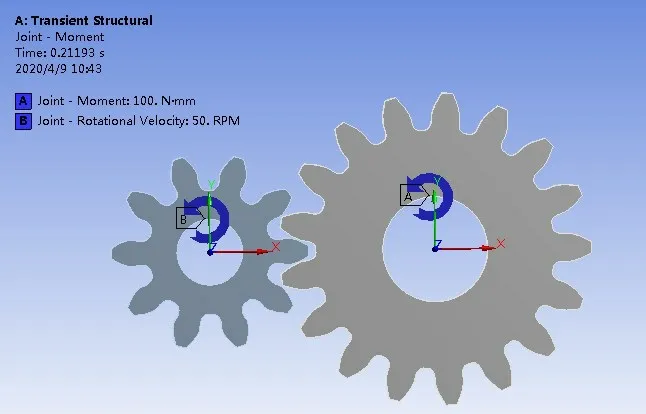
图4 边界条件的设定

3 瞬态动力学强度分析

3.1 塑料齿轮齿面应力结果分析

Equivalent（von-mises）stress 的应力分布图如图5 所示.从图中可以看出，主、被动齿轮的齿根部位处的应力较大，其应力最大值可以作为该齿所受到的弯曲应力.由分析可知，塑料齿轮在啮合动态过程中，若承载较大，易出现轮齿折断现象，这是塑料齿轮失效的形式之一.在设计塑料齿轮传动系统时，要特别注意避免齿根断裂现象的出现.

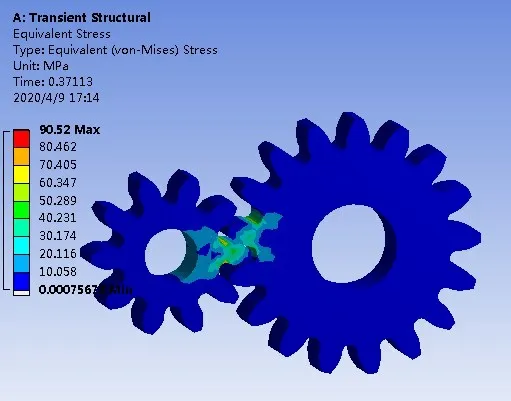
图5 齿轮Von-mises应力分布

塑料齿轮动态啮合过程中的最大应力值随着啮合时间变化的曲线如图6所示.由于齿轮重合度的原因，齿轮表面始终在双齿啮合区→单齿啮合区→双齿啮合区进行往复循环.从图中可以看出，齿轮齿面在啮合区改变的时候会出现最大应力的突变，由于齿侧间隙和啮合刚度的共同作用，出现齿面冲击现象，齿面冲击易造成齿轮折断损坏.在每个啮合接触区域内，最大应力都会出现两次突变点，这是因为齿侧间隙的存在，导致啮合齿轮在进入或退出啮合区时，存在非接触时刻，系统的接触刚度变化，进而导致应力出现突变.齿侧间隙对塑料齿轮系统有显著影响，是塑料齿轮系统的非线性因素之一.对比单齿啮合区和双齿啮合区的最大应力情况，从图中可知，双齿啮合区最大应力值相对单齿啮合区最大应力值较低，因此在设计塑料齿轮传动系统中，选择合理的参数增加双齿啮合区的时间范围，必然会降低单齿啮合区的时间范围，对塑料齿轮传动系统更有利，使得塑料齿轮啮合过程中的应力分布更加均匀，延长使用寿命.

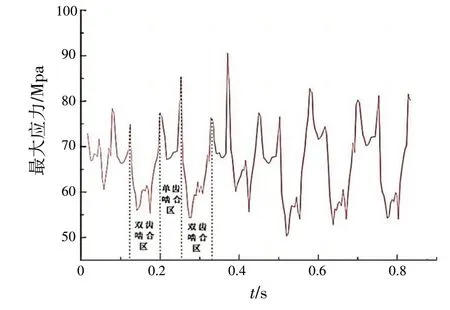
图6 齿面最大应力随着啮合时间变化

3.2 塑料齿轮齿面变形量分析

选取被动齿轮的齿面作为求解跟踪面.被动轮齿面三方向变形量随着时间的变化曲线如图7所示.图中可知齿面在轴向（Z向）变形量几乎为0，变形主要表现在横向（X向、Y向）.在设计塑料直齿轮齿轮传动系统时，往往可以忽略轴向振动，主要考虑横向振动.在塑料齿轮啮合过程中，横向变形量（Y向）随着时间的增加先增大后减小，主要是因为啮合齿轮对数的变化导致刚度的变化.塑料齿轮系统由于材料自身的原因，弹性模量和强度都较小，无法适用于重载或扭矩大的场合.在机械传动中，塑料齿轮更适用于轻载场合且由于变形量大，往往会导致传动比的改变，进而造成输出转速或者转矩无法满足使用要求.在设计塑料齿轮传动系统中，需要考虑因为齿面变形导致的齿轮传动比变化.

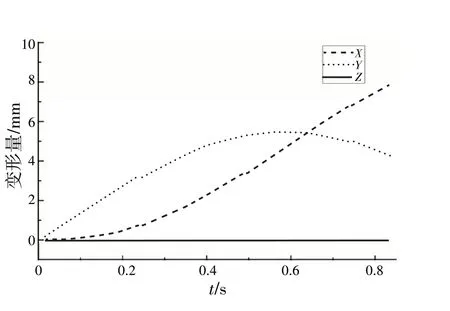
图7 齿面变形量随着啮合时间变化的曲线

4 结论

文中通过UG 软件建立了包含齿侧间隙的塑料齿轮系统模型并导入Ansys Workbench 进行瞬态动力学分析，通过设定齿面摩擦和啮合刚度参数，得到塑料齿轮的动态啮合特性.仿真分析表明，塑料齿轮啮合过程中的齿根应力最大，易发生齿根断裂现象，也易出现齿面冲击现象.由于齿面横向变形量大，设计过程中需要考虑由于齿面变形导致的传动比改变.

[责任编辑 郭 涓]