基于最佳滑移率的摩托车转弯制动系统设计

张晓东，潘 茹

（1.宁德师范学院 信息与机电工程学院，福建 宁德 352100；2.国网宁夏电力有限公司 超高压公司，宁夏 银川 750010）

汽车极大方便了人们的出行，然而汽车数量的增加也引发了城市交通拥堵、停车困难等诸多问题.摩托车因轻便灵活、占地面积小，在拥堵的城市中具有更高的机动性和出行效率，现已成为群众短途出行的重要交通工具之一.根据中国公安部交通管理局发布的数据，2021年全国摩托车新注册登记1 005万辆，比2020年增加了179万辆[1].摩托车的平均行驶速度高达80 km·h-1，然而摩托车结构类似于倒单摆，属于静态不稳定系统，在转弯情况下具有较大的侧倾角，存在车辆侧翻的风险.如果在转弯工况下施加制动，则侧翻风险急剧增加.近年来，随着智能控制技术的发展，主动安全系统如电子稳定程序(electrical speed controller,ESC)、车辆稳定控制(vehicle stability control,VSC)等已广泛应用于汽车，有效提高了汽车的安全性，然而在摩托车领域应用较少.在中国制造向高质量发展的大背景下，摩托车由量产转向高端制造已成必然趋势，而且民众的骑行安全意识也在逐渐提高，研究和开发摩托车主动安全系统，提高摩托车的安全性具有重要的现实意义[2-3].

制动系统是摩托车主动安全系统的重要组成部分，用于摩托车的防抱死制动系统(antilock brake system，ABS)于20 世纪80 年代末推出，通过在硬制动时保持车轮旋转从而缩短制动距离.试验表明：ABS 通常提供更短的停车距离，增加制动稳定性，防止摩托车手摔倒[4].为进一步提高制动性能，诸多学者开展了相关研究.Ganesh 等[5]提出了变制动力系统，该系统根据轮胎与地面之间的垂直载荷改变有效制动盘半径来调整制动力；Thomas 等[6]提出了摩托车稳定控制(motorcycle stability control,MSC)系统，该系统结合了ABS、电子制动系统、牵引力控制和惯性传感器，根据车辆状态，调整制动或者牵引力以提高车辆安全性；Baumann 等[7]使用模型预测控制算法(model predictive control,MPC)在前轮和后轮之间分配制动力，以减少转弯时的转向力矩，以保持车辆方向稳定性；More 等[8]基于线性PID 控制策略，设计了用于摩托车的防抱死制动系统，电子控制单元根据轮速、车速计算滑移率，并反馈给PID 控制器，PID 控制器调整制动力矩以控制轮胎的滑移率为参考滑移率（-0.2）；吴龙辉[9]通过分析摩托车制动器制动力、地面制动力与附着力之间的关系提出了摩托车在不同附着系数路面上前后轮制动器制动力理想分配曲线；Soni 等[10]通过分析直线与转弯工况中的车辆侧倾角、车身和路面摩擦系数的影响，确立前后轮制动力分配方法，并设计了联合制动系统，最后利用BikeSim 和Simulink 软件进行联合仿真，验证其合理性；Melnikov 等[11]提出的制动控制策略通过识别地面对车轮侧向作用力的导数产生控制信号，当侧向作用力导数为负，则轮胎出现侧滑，有失稳的趋势，应重新调整制动力，该系统类似于汽车的电子稳定控制系统(electronic stability program,ESP)，增加了摩托车的制动稳定性和可控性；Lin 等[12-13]基于自适应控制算法提出了可变联合制动系统，前后轮的制动器制动力分配比通过自适应算法进行调整；Fernandez 等[14]提出了基于模糊逻辑的防抱死制动系统，摩托车参数经过扩展性卡尔曼滤波器估测出滑移率与路面附着系数.将当前滑移率与最佳滑移率的偏差及偏差变化率、路面附着系数输入至模糊逻辑产生控制命令，为改善模糊逻辑控制性能，采用协同进化算法进行控制参数优化；Phalke等[15]考虑悬架的影响，提出了前后轮联合制动时的制动力最佳分配方法.

综合上述研究现状：文献[6，7，9，10，12，13]只是基于防止轮胎抱死的角度，提出了摩托车制动系统，缺少对轮胎模型的系统研究.轮胎是车辆的重要组成部分，轮胎与地面的接触力对车辆制动时的稳定性起着关键作用.文献[8]基于轮胎滑移率进行制动控制，直接将最佳滑移率定义为纵向力最大时的对应值（-0.2），该制动策略在直线行驶制动时具有较高的制动性能，但是在转弯情况下，可能会因侧向力不足造成失稳.文献[11]提出基于侧向力变化率的制动系统保证了车辆的稳定性，但是对制动性能缺少相关分析.文献[14]和[15]提出的制动系统主要适用于直线制动情形.Pacejka[16]的研究表明：当摩托车转弯制动时，除了纵向制动力外，还存在由地面施加的侧向力来抵消离心力.充足的侧向力是保证车辆稳定的重要因素，但纵向力和侧向力受摩擦椭圆的影响.鉴于此，文中通过轮胎模型分析纵向与侧向特性并建立最佳滑移率决策模型，基于模糊PID 算法建立制动系统，最后利用Matlab/Simulink 和BikeSim联合仿真对所提出的转弯制动系统的制动性能进行仿真以验证其合理性.

1 摩托车轮胎建模

车辆通过轮胎与地面接触，地面对轮胎的作用力直接影响车辆的驱动、制动和转向过程中的操纵稳定性.地面对轮胎的作用力与轮胎运动情况相关，轮胎建模旨在建立轮胎运动与地面作用力之间的数学模型.轮胎模型的输入与输出变量如图1所示.

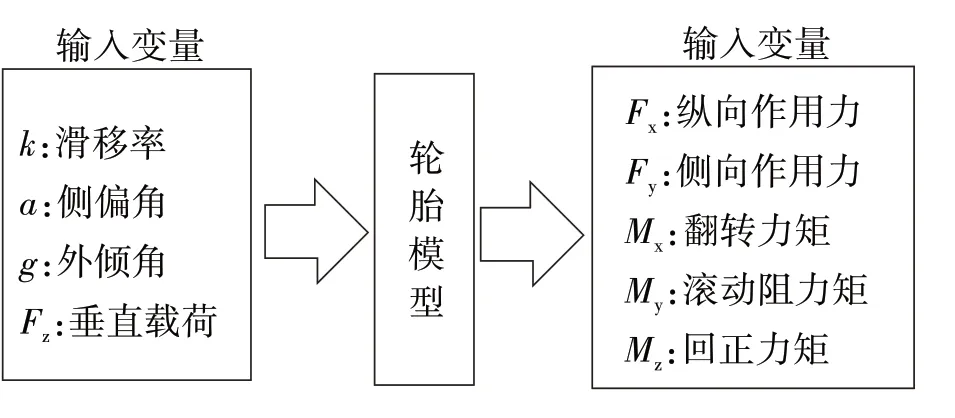
图1 轮胎模型的输入与输出变量

为描述轮胎的运动学与力学参数，建立轮胎坐标系如图2所示.坐标系原点O为轮胎面和地面的交线与车轮旋转轴线在地平面上投影线的交点；车轮面与地面的交线为x轴，向前为正方向；z轴垂直于地面，向上为正方向；根据右手定则，y轴方向随之确定.相关运动学与动力学参数如图2标注所示.

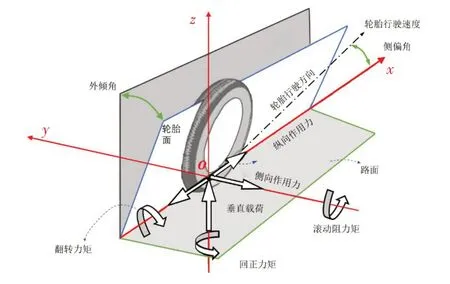
图2 轮胎坐标系与相关参数

轮胎行驶方向示意图如图3 所示.轮胎受到路面侧向倾斜、侧向风力或离心力作用时，地面对轮胎产生侧向作用力（Fy），由于轮胎侧向弹性的因素，行驶速度方向偏离轮胎面，发生侧偏现象，速度方向与x轴的夹角为侧偏角（α）.侧偏角是影响轮胎侧向力的重要因素.行驶速度（V）在x轴和y轴的投影分别为纵向速度（Vx）和侧向速度（Vy）.当摩托车在转向制动情况下，除了存在侧偏现象外，胎面与地面发生一定程度的相对滑动，轮胎处于边滚边滑的状态，即存在纵向滑移速度（Vsx）与侧向的滑移速度（Vsy），其中侧向滑移速度等于（Vy）.

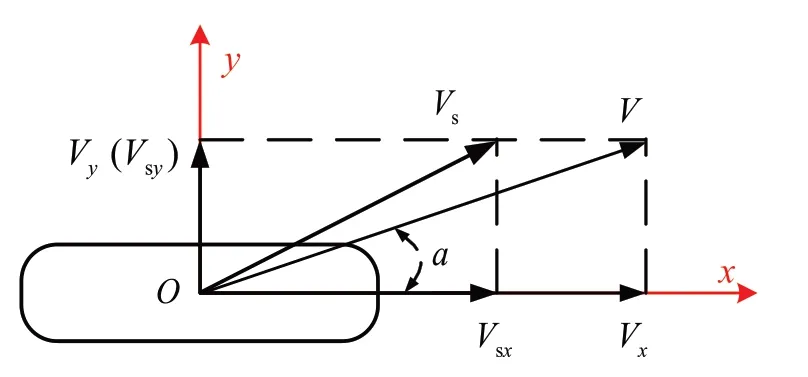
图3 轮胎速度示意图

纵向滑移率是轮胎产生纵向力的重要因素.纵向滑移率（κ）和侧偏角（α）的计算式如下

在地面对轮胎的作用力中，纵向作用力直接影响车辆制动性能，侧向力对车辆稳定性具有重要影响.当摩托车转弯制动时，地面对轮胎同时施加纵向力与侧向力，其中侧向力用于抵消曲线运动产生的离心力，以保持车辆平衡，因此轮胎纵向和侧向特性对车辆转弯制动至关重要.为此首先需要建立轮胎力学模型，轮胎模型具有高度非线性，目前具有代表性的轮胎力学模型有：刷子模型、Filala模型、统一轮胎模型和魔术公式.其中，刷子模型、Fiala 模型和统一模型以汽车轮胎为研究对象，针对摩托车轮胎的研究较少.相比于汽车轮胎，摩托车轮胎具有较大的侧倾角，Pacejka[16]提出的魔术公式是一种经验模型，通过三角函数的组合拟合轮胎实验数据，模型精度高、形式统一、鲁棒性强，对摩托车轮胎也进行了深入研究.魔术公式已经有较为成熟的应用，如美国MSC 开发的BikeSim 软件集成大量的轮胎实验数据.魔术公式正在成为轮胎行业的标准.鉴于此，采用魔术公式建立轮胎模型.

当轮胎只有纵向滑移，没有侧向滑移时，纵向力计算式为

式中：Bx为刚度因子；Cx为形状因子；Dx为峰值因子；Ex为曲率因子.水平位移SHx和垂直位移SVx分别表示帘布层转向效应、圆锥度和滚动阻力的影响.

当轮胎同时存在纵向与侧向滑移时，引入权重因子Gxα表征侧向滑移对纵向力的影响.纵向力计算式为

同理，在纯侧向滑移工况下，侧向力计算式为

对于联合滑移工况，引入权重因子Gyκ表征纵向滑移对侧向力的影响.联合滑移时的侧向力计算式为

在式(3～6)中，刚度因子、形状因子、峰值因子和曲率因子受滑移率、侧偏角、外倾角等运动学和动力学参数的影响.以180/55ZR17 摩托车轮胎为研究对象，借助BikeSim 软件得到该轮胎的魔术公式参数.通过Matlab 软件建立轮胎模型，并将BikeSim 中的参数代入模型中.令滑移率、侧偏角和垂直载荷取不同的值，分析轮胎的纵向与侧向特性.

轮胎纵向特性如图4 所示.由图可知：当滑移率为0.15～0 时.纵向力随着滑移率绝对值的增加而增加，当滑移率进一步增加，纵向力下降.因此在制动工况下，滑移率绝对值过大会导致制动性能减弱.当车辆处于转弯制动工况时，轮胎同时存在纵向滑移和侧偏现象.由图4（a）可知：侧偏角度越大，纵向力越小，摩托车在制动过程中前后轮会发生荷载迁移，造成前后轮垂直载荷的变化；由图4（b）可知：不同垂直载荷时的最大纵向力所对应的滑移率约为-0.15，摩托车与汽车最大的不同在于外倾角，汽车外倾角较小，摩托车转弯工况下具有较大的外倾角；由图4（c）可知：轮胎倾斜一定程度上导致纵向力减小.

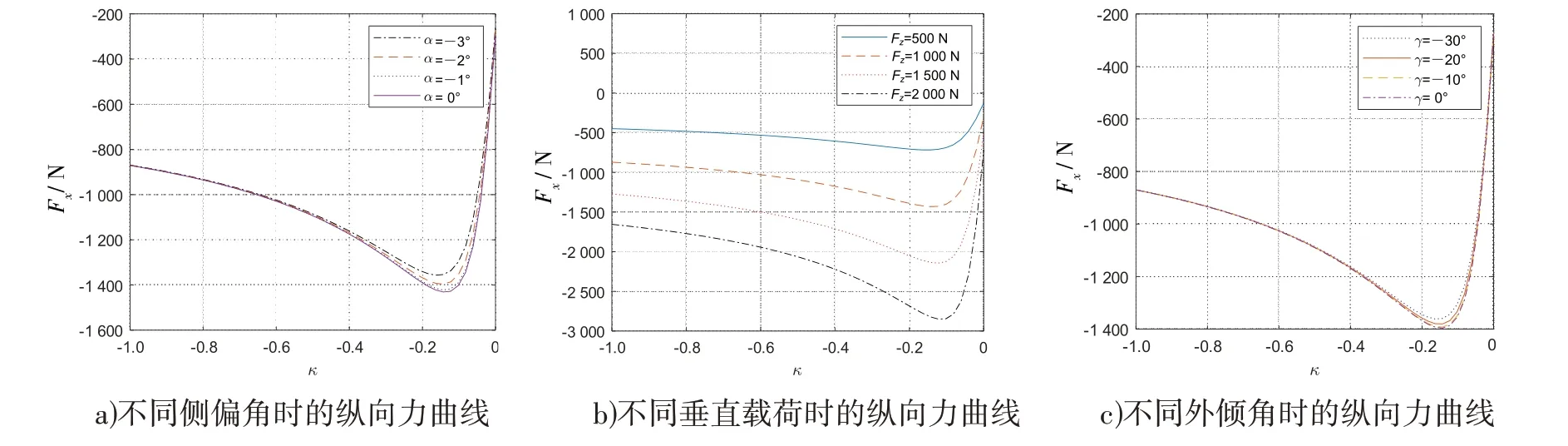
图4 轮胎的纵向特性

轮胎侧向特性如图5 所示.在转弯制动工况下，侧偏角较小时，地面对轮胎的侧向力与侧偏角呈线性变化.侧偏角超过5°，侧向力趋于定值，轮胎发生侧滑.由图5（a）可知：滑移率越大，地面能够提供的侧向力越小，当轮胎抱死，滑移率为-1，侧向力几乎为0，此时车辆将发生严重的侧滑；图5（b）为外倾角γ取不同值时对侧偏特性的影响，外倾角越大，地面能够提供的侧向力越小，摩托车在转弯工况下存在较大的外倾角，应注意防止侧滑现象；纵向力对侧偏特性的影响如图5（c）所示，纵向力与侧向力组成的摩擦椭圆，在侧偏角一定的情况下，随着纵向力的增加，由于轮胎侧向弹性的改变，侧向力有所减小.当纵向力很大时已经耗去大部分附着力，而侧向能利用的附着力减少.因此在转弯制动工况下，片面追求制动性能容易导致侧向力不足造成侧滑，需要保证侧向稳定的前提下进行制动.

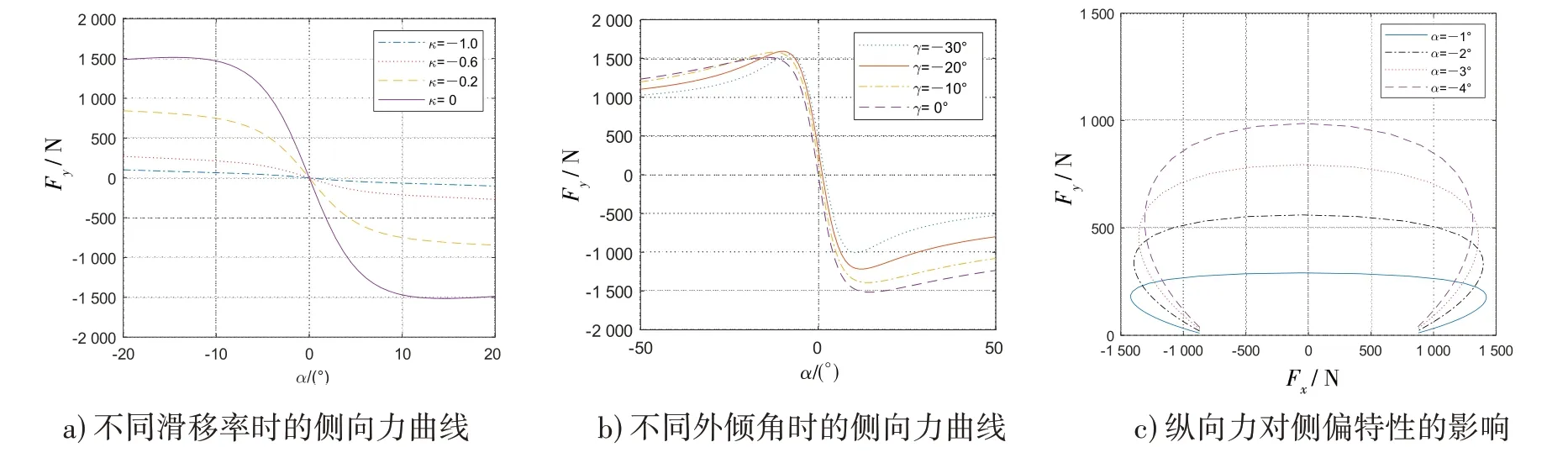
图5 轮胎侧向特性

综合上述轮胎特性分析可知：地面对轮胎的作用力受到滑移率、侧偏角、外倾角、垂直载荷的影响，其中滑移率可控性强，通过调整滑移率可以同时控制纵向力与侧向力，滑移率越靠近0，侧向力越大.当滑移率为-0.15时，纵向力最大，侧向力有所减小.摩托车转弯制动过程中，既需要侧向力保持车辆稳定，又要有纵向力确保车辆制动停车，滑移率可以作为转弯制动控制系统的输入，实现对车辆稳定性与制动性的控制.

2 最佳滑移率决策模型

摩托车转弯工况下的受力如图6 所示，车身倾斜一定角度以平衡离心力.车身倾斜角（φ）导致轮胎产生外倾角（γ）.在稳定转弯的情况下，车身侧倾角与轮胎外倾角相同，根据力平衡原理，作用在车轮上的离心力的计算式为

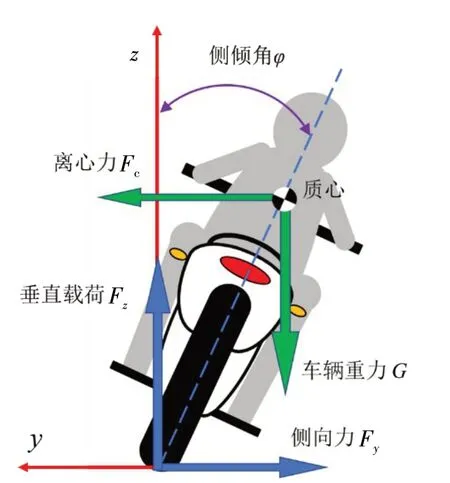
图6 摩托车转弯受力示意图

式中:FC为离心力；φ为侧倾角.车身侧倾角越大，产生的离心力越大，需要地面提供更大的侧向力（Fy)来保持车辆稳定.

当摩托车在转弯刹车时，两个车轮同时受到纵向力和侧向力的作用.纵向力属于制动力，决定了制动性能，侧向力则关系到车辆的稳定性.轮胎模型分析表明：横向力和纵向力受滑移率的影响，因此这两个力可通过改变滑移率来控制.适当的滑移率可以让车辆安全稳定的制动.摩托车失稳主要表现为侧倾角急剧增大发生倾覆，因此对轮胎制动的最佳滑移率由较大时，摩托车有倾覆的危险，应减小滑移率，让地面提供足够的侧向力保持车辆稳定.当较小时，摩托车相对安全，可适当调整滑移率接近-0.15，地面提供足够的制动力.鉴于前轮侧滑导致的倾覆风险高于后轮，经过反复试验，令常数C取3，前轮采用高斯隶属函数确立前轮最佳滑移率，高斯隶属函数如式(8).前轮控制策略如图7所示.

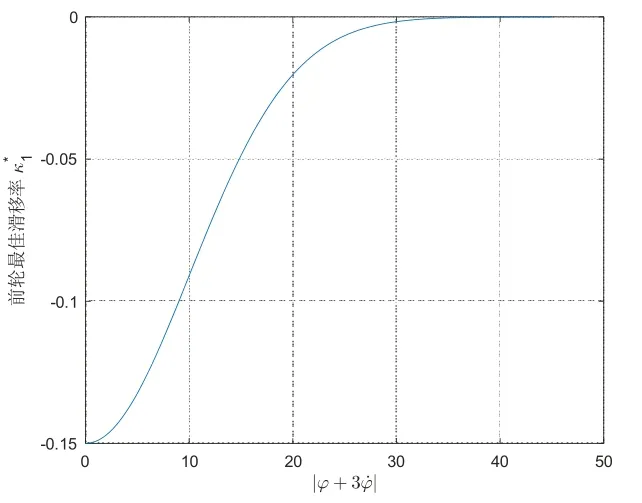
图7 前轮最佳滑移率决策模型

后轮控制策略如图8所示.后轮采用线性函数确定最佳滑移率，即

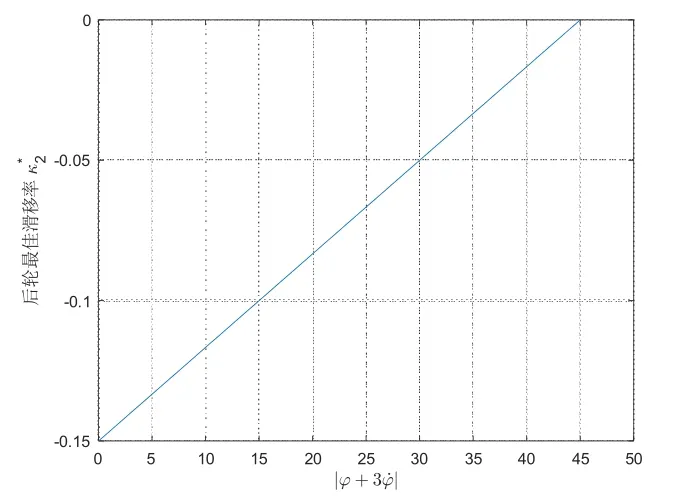
图8 后轮最佳滑移率决策模型

3 转弯制动系统设计与仿真

摩托车转弯制动控制系统结构如图9 所示.该系统由3 部分组成：前后轮最佳滑移率决策模型、控制系统和摩托车动力学模型.摩托车侧倾角与侧倾角速度输入至前后轮最佳滑移率决策模型产生最佳滑移率，最佳滑移率与当前滑移率差值输入至控制系统，控制系统产生控制信号控制前后轮滑移率，车辆动态反馈至滑移率决策模型和控制系统，形成了闭环控制.

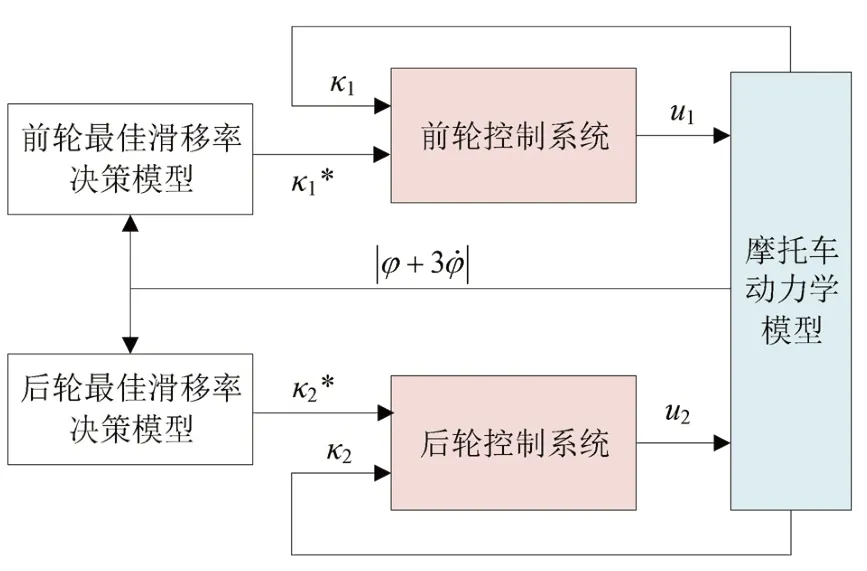
图9 摩托车转弯制动系统示意图

摩托车在静止状态不能保持稳定，转弯工况下侧倾角较大，是一个高度非线性系统.鉴于BikeSim 软件在仿真摩托车动力学方面的成熟应用，采用BikeSim 模拟图9中的摩托车动力学模型.摩托车属于非线性系统，控制策略应该具备自适应、学习、推理功能[17].智能控制技术如模糊逻辑控制、神经网络、滑模控制等为控制系统设计理论依据.其中，模糊逻辑控制原理如图10 所示.该控制策略不依赖被控对象的数学模型，而是以人对被控对象的控制经验和知识为依据，建立数据库和规则库.控制系统可以根据知识库与规则库进行模糊推理，向被控对象给出控制命令.模糊控制适用于传统控制方式难以解决的问题，如建模困难、多变量强耦合、高度非线性等，对高度非线性系统具有鲁棒性.然而，模糊控制的精度在很大程度上取决于数据库和反复测试的规则库，不易消除静态误差.

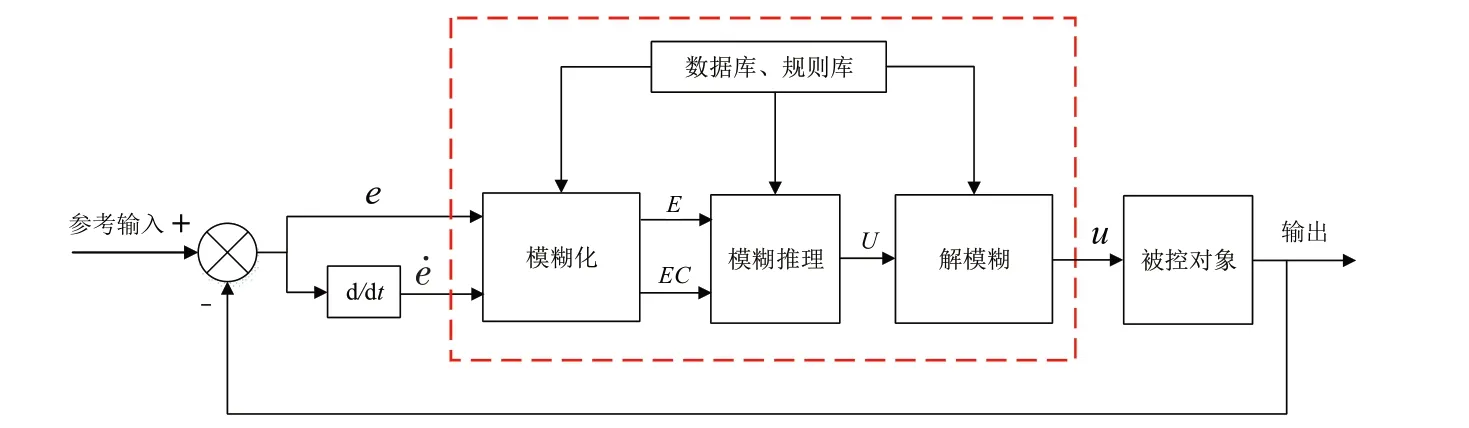
图10 模糊控制原理

针对模糊控制容易存在稳态误差的不足，采用模糊PID 控制策略对摩托车进行控制，模糊PID 控制由模糊逻辑和PID 控制器组成.PID 控制器由于其简单、精确等优点，在许多领域得到了广泛的应用.然而，对于数学模型未知的高度非线性系统，传统PID控制参数如比例系数、积分系数、微分系数等固定不变，影响控制性能.模糊逻辑为PID参数自整定提供了可能，模糊PID控制系统原理如图11所示.根据输入误差和及其变化率，采用模糊逻辑对PID 参数进行调整，既消除了稳态误差，又提高了控制系统的自适应性.

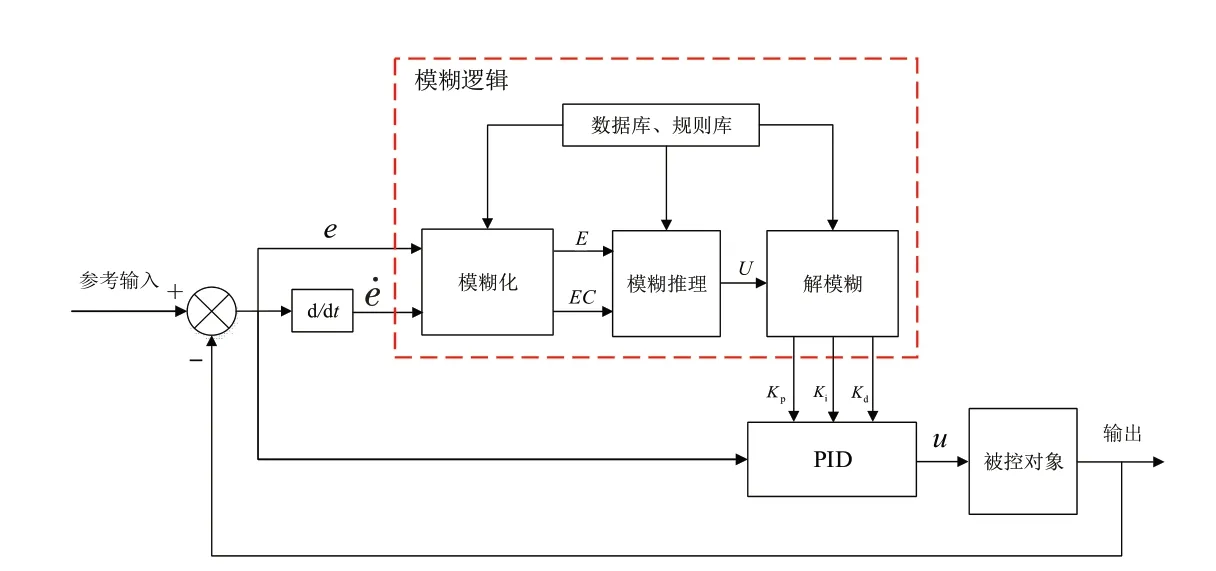
图11 模糊PID控制系统

为验证转弯制动系统的合理性，根据图9 在Matlab/Simulink 环境中创建转弯制动系统仿真模型，包括最优滑移率决策模型和模糊PID 控制器.BikeSim 仿真的摩托车动力学参数通过交互接口传输至Simulink，由此形成BikeSim与Matlab的联合仿真.

基于最佳滑移率的制动系统仿真结果如图12所示.摩托车初始状态如图12（a）所示，所示初始速度为80 km·h-1，初始侧倾角为-21°.摩托车开始制动，其动力学参数变化曲线如图12(b～f).在3.5 s内车身侧倾角〔图12(b)〕逐渐减小至5°，同时车速〔图12(c)〕也降低至0，摩托车平稳停车.当车速较小且侧倾角也较小的情况下，轮胎抱死，制动效率高.在3.3 s时，速度小于5 km·h-1，两个轮胎抱死，轮速存在一定的突变.前后轮侧偏角变化曲线如图12(d)所示，侧偏角在-2°和2°之间，因此制动系统具有较好的方向稳定性.制动减速度和制动距离如图12(e)和图12(f)所示，平均制动减速度为-6.6 m·s-2，制动距离为40 m，验证了制动系统具有优良的制动性能.前后轮滑移率变化曲线如图12(g)和图12(h)所示，由于侧倾角与侧倾角速度的变化，前后轮最佳滑移率随之实时调整，兼顾了制动性与方向稳定性，轮胎滑移率与最佳滑移率保持一致，模糊PID控制性能良好.

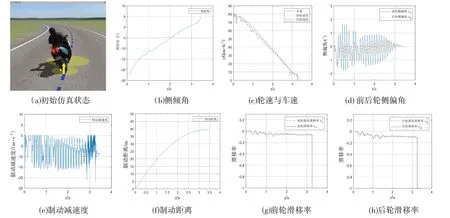
图12 基于最佳滑移率的制动系统仿真

根据轮胎动力学分析，最大附着系数出现在滑差率在-0.15 至-0.2 之间，传统的防抱死制动系统往往将制动系统的最佳滑移率固定为-0.2.为了进行对比分析，应用文献[8]的ABS对转弯的摩托车进行制动仿真，该制动系统的最佳滑移率为固定值（-0.2）.除了最佳滑移率不同外，设定相同的仿真条件：初始车速为80 km·h-1，初始侧倾角为-21°，仿真结果如图13 所示.由图13（a）可知：1 s 内车身侧倾角度迅速增大到80°左右，摩托车突然发生侧翻；由图13（b）可知，由于侧向力不足，两个轮胎侧滑角发生较大变化，导致侧滑翻车，将滑移率固定为-0.2不适用于转弯制动情形，最佳滑移率宜根据车辆动态实时调整，通过对比两种制动系统的性能，验证了所提出的转弯制动系统提高了摩托车的制动性和方向稳定性.

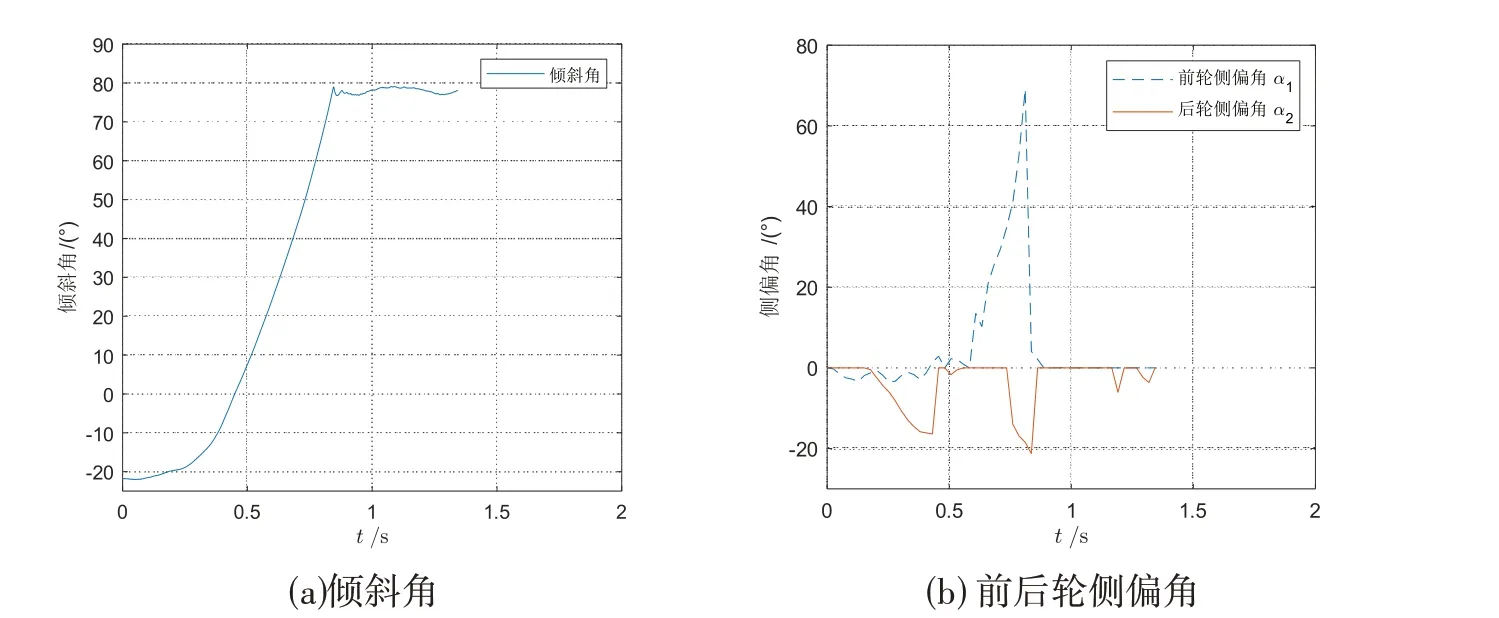
图13 基于固定滑移率的制动系统仿真

4 结论

摩托车是日常生活中常用的短途交通工具，但固有的不稳定性导致转弯和制动过程中存在安全隐患.因此，对摩托车主动安全系统的研究具有重要的现实意义.通过分析摩托车轮胎模型特性确立了最佳滑移率决策模型，提出了基于模糊PID 的转弯制动控制系统.通过Matlab 与BikeSim 联合仿真验证了控制系统的有效性，并与传统ABS进行了对比研究，得到如下几点主要结论.

1）分析了滑移率、侧偏角、外倾角和垂直载荷对轮胎纵向与侧向特性的影响.结果表明：通过调整滑移率可以同时控制纵向力与侧向力，滑移率越靠近0，侧向力越大；当滑移率为-0.15时，纵向力最大，侧向力有所减小.确立滑移率作为转弯制动控制系统的控制变量.

2）基于轮胎特性分析，借助高斯函数与线性函数确立了最佳滑移率决策模型，模型的输入为车身侧倾角与侧倾角速度加权和，输出为最佳滑移率.由此实现最佳滑移率随着摩托车运动参数的变化而调整，是兼顾制动性能和车辆稳定性的最优解.

3）提出基于模糊PID 的转弯制动系统，该系统由最佳滑移率决策模型和模糊PID 控制器组成.最佳滑移率决策模型根据车辆运动参数及时调整最佳滑移率并输入至模糊PID 控制器，控制器产生控制力矩作用于轮胎，以控制滑移率，进而控制车辆动态，车辆动态再反馈至制动系统形成闭环控制.Matlab与BikeSim 联合仿真结果表明：所提出的转弯制动系统能合理调整最佳滑移率，车速在3.5 s内从80 km·h-1降为0 km·h-1，而且轮胎侧偏角不超过2°，没有发生侧滑，制动系统具有良好的制动性和方向稳定性.

转弯制动系统需要车速、侧倾角和侧倾角速度，然而目前的传感器很难直接准确测量以上参数，可通过惯性测量单元得到的运动学参数进行状态估测，从而获得制动系统所需的车速、侧倾角等信息.未来将开展车速和车身侧倾角估测方面的研究.

[责任编辑 郭 涓]