具变指数非线性项的强阻尼波动方程的爆破

李海霞, 曹春玲

(1. 长春师范大学 数学学院, 长春 130032; 2. 吉林大学 数学学院, 长春 130012)

0 引 言

考虑如下具变指数非线性项的半线性强阻尼波方程的初边值问题:

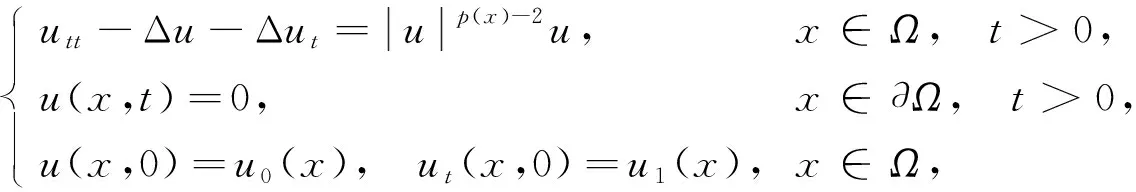
(1)

其中Ω⊂n(n≥1)是具光滑边界∂Ω的有界区域,p(x)是Ω上的可测函数,

目前, 关于初边值问题

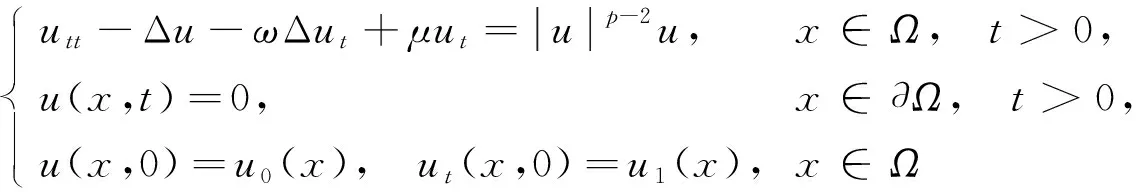
(2)

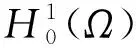
另一方面, 具变指数的发展方程近年来也备受关注[6-9]. 关于具变指数的弱阻尼波动方程的爆破结果, Messaoudi等[10]考虑了如下波动方程:

(3)

其中a和b是正常数,m(·)和p(·)是可测函数.在对问题(3)建立了弱解的存在唯一性之后, 文献[10]得到了一个负初始能量时的有限时刻爆破结果.Messaoudi等[11]将上述爆破结果推广至如下拟线性弱阻尼波动方程上:

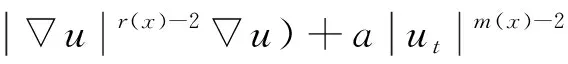
(4)

此外, 还将上述问题的爆破条件推广为适当小的正初始能量.

对具变指数项的半线性或拟线性强阻尼波动方程的爆破研究目前也有一些结果. 例如: Antontsev[12]研究了拟线性波动方程

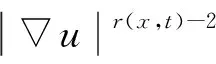
(5)

当参数和变指数满足一定条件时, 证明了该问题弱解的局部存在性以及负初始能量条件下弱解的有限时刻爆破, 但当初始能量非负时, 对问题(5)是否存在有限时刻爆破解未给出回答; Park[13]研究了问题(5)的一个特例, 即问题(1)的爆破性质, 利用Levine[14]的凹方法, 得到了当初始能量有正上界时问题(1)的一个爆破结果.

1 预备知识

设p:Ω→[1,∞)是一个有界可测函数, 并记

变指数Lebesgue空间Lp(x)(Ω)定义为

该空间在被赋以范数(Luxemburg范数)

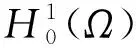
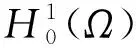
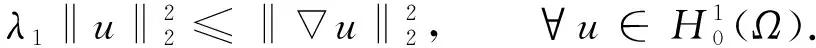
(6)

引理1[15]设p:Ω→[1,∞)是有界可测函数, 且满足

2≤p(x)<∞,n=1,2;

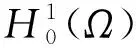
本文考虑问题(1)在下述意义下的弱解u(x,t).在不产生歧义时,u(x,t)也常被简记为u(t).弱解的局部存在和唯一性可通过适当修改文献[4,10]中的方法得到.

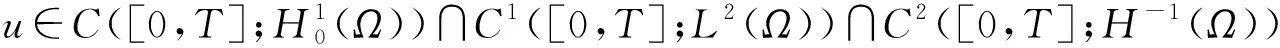
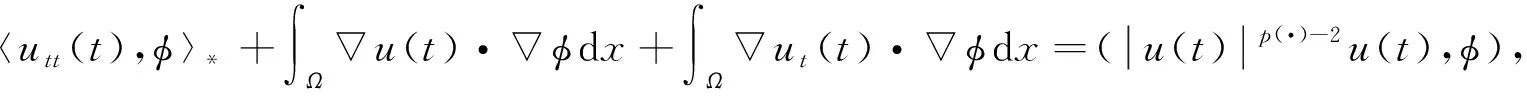
(7)

则称u(x,t)为问题(1)在[0,T]上的一个弱解.

假设条件:

(H2) 对数型Hölder连续性条件: 存在A>0及δ∈(0,1), 使得对几乎所有满足|x-y|<δ的x,y∈Ω, 均有

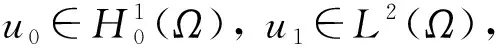
记Tmax为问题(1)弱解u=u(t)的最大存在时间, 并定义能量泛函、 Nehari泛函与不稳定集分别为

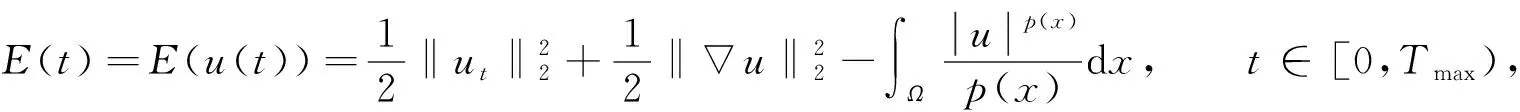
(8)

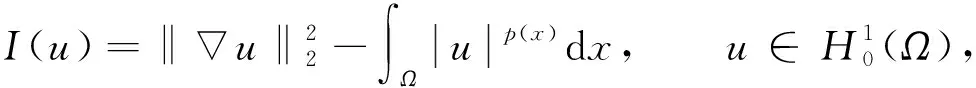
(9)

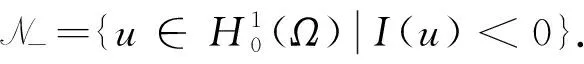
(10)

在式(7)中取φ=ut可得能量恒等式:

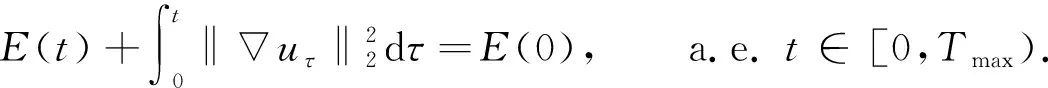
(11)

式(11)表明E(t)关于t在[0,Tmax)上是单调不增的.

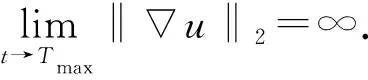
事实上, 利用与文献[4]中证明定理3.1类似的讨论和连续延拓定理[16]可知, 如果Tmax<∞, 则

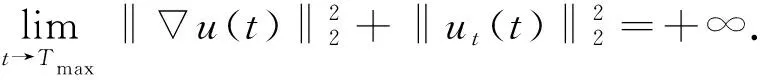
(12)

于是, 由式(8),(11)和Sobolev不等式可得

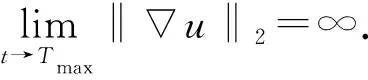
定义2设u(t)是问题(1)的弱解,Tmax是它的最大存在时间.若Tmax<∞, 则称u(t)在有限时刻爆破, 并称Tmax是u的爆破时间.若Tmax=∞, 则称u(t)是整体存在的.

2 主要结果

引理2[14,17]假设ψ(t)是一个正的二次可微函数, 且满足

ψ″(t)ψ(t)-(1+θ)(ψ′(t))2≥0,

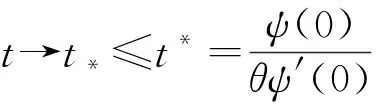
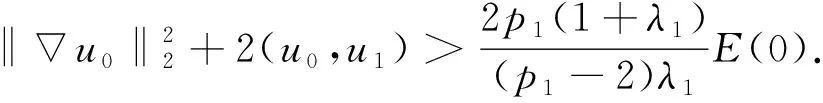
(14)

则问题(1)的解u(t)在有限时刻爆破, 且爆破时间Tmax的上界满足如下估计:

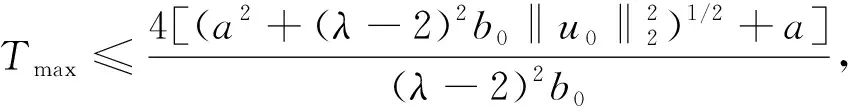
(15)

其中λ,a,b0是确定的常数.

证明: 证明过程分为4步.

表明F(t)在(0,Tmax)上严格单调递增.

2) 证明u(t)∈N-,t∈[0,Tmax).若不然, 则由连续性及假设条件I(u0)<0可知, 存在t0∈(0,Tmax), 使得

I(u(t))<0,t∈[0,t0),

(17)

I(u(t0))=0.

(18)

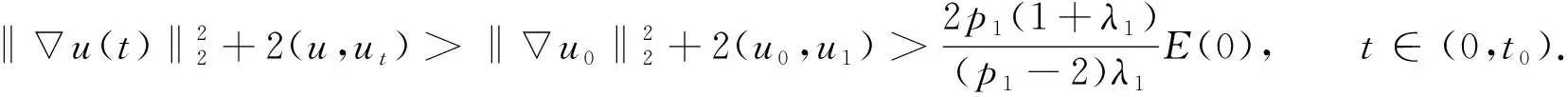
(19)

注意到F(t)的连续性和单调性, 由式(19)得

(20)

另一方面, 由式(8)和式(9)得

由式(6),(11),(18),(21)和Cauchy-Schwarz不等式, 可得

与式(20)矛盾.故结论成立.

3) 通过选取适当的参数并结合Levine凹方法证明Tmax<∞.若不然, 假设u是问题(1)的整体解, 则Tmax=∞.类似于文献[13]中的证明, 对任意T>0,b>0,η>0, 定义

(23)

则G(t)>0,t∈[0,T],

由式(24)得

利用Cauchy-Schwarz不等式知

(u,ut)≤‖u‖2‖ut‖2,

(27)

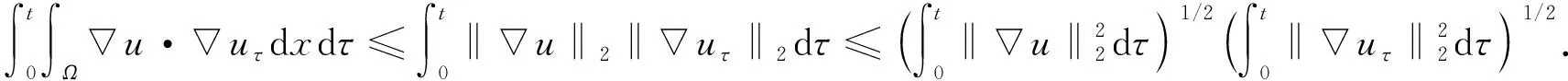
(28)

将式(27),(28)与Cauchy不等式相结合, 进一步可得

对任意的λ∈(2,p1).注意到式(23),(25),(29)可得

其中

由式(6),(8),(11),(9)知

下面取

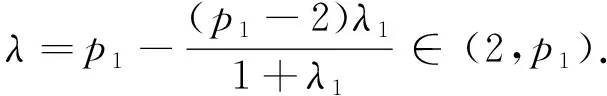
(32)

由式(31)及F(t)的单调性知, 对任意的

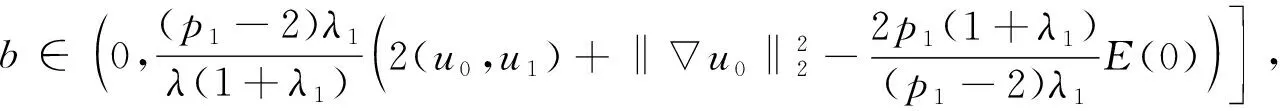
(33)

均有

于是, 结合式(30)和式(34)可知, 对任意满足式(33)的b, 均有

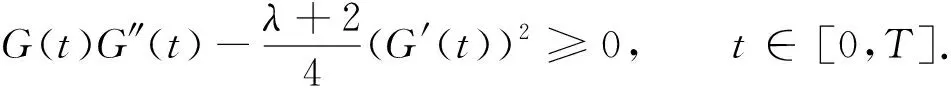
(35)

选取不依赖于T的η满足

(36)

则

且对充分大的T有

(37)

对G(t)应用引理2可知, 存在t*>0满足

(38)

使得

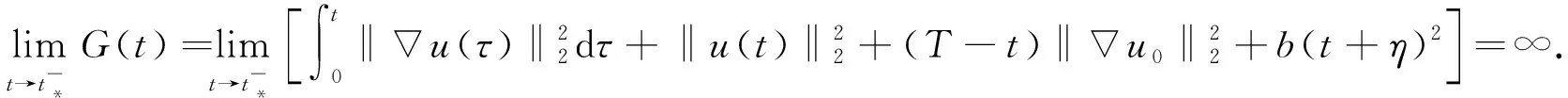
(39)

由式(39)易知

(40)

由注1知, 式(40)表明u(t)在t*时刻爆破.这与u(t)是问题(1)的整体解矛盾.故Tmax<∞.

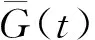
利用平行于3)的证明, 可得

其中

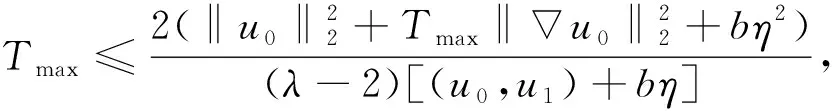
(41)

λ仍由式(32)给出,b满足式(33).如果仍要求η满足式(36), 则式(41)可改写为

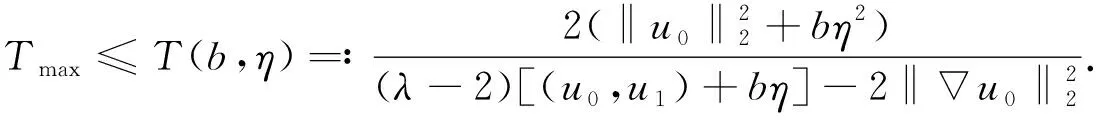
(42)

固定b满足式(33).记

直接验证易知T(b,η)在η=η0处取到其在

上的最小值, 且

最后, 令函数T(b,η0)关于b在式(33)上取最小值, 得

其中

综上, 由式(42)可知

证毕.

此外, 对任意的D>0, 存在α2>0, 使得

根据定理2知, 问题(1)以(u0,u1)为初值的解u(x,t) 在有限时刻爆破, 且初始能量满足E(0)=D.

下面给出问题(1)爆破时间的一个下界估计.由于爆破时间的下界可以为所考虑的系统提供一个安全(稳定)区间, 所以在实际应用中非常重要.

定理3若p(x)满足假设条件(H1)和(H2),u(x,t)是问题(1)的一个在Tmax时刻爆破的弱解.则Tmax可从下方估计为

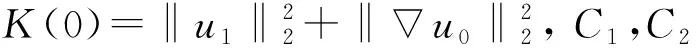
证明: 先利用特定泛函满足的一阶微分不等式得到爆破时间的一个下界估计.为避免证明过程冗长, 这里只给出n≥3时的证明(n=1,2时类似可证).记

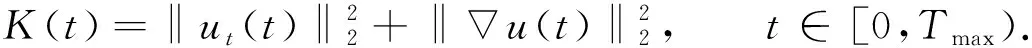
(43)

由于u(x,t)在Tmax时刻爆破, 因此由式(12)知

(44)

直接计算可得

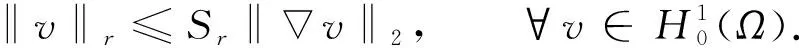
(46)

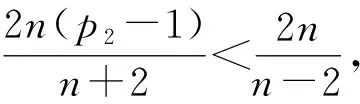
K′(t)≤C1+C2Kp2-1(t),

(48)

表明对任意的t∈[0,Tmax)均有

(49)

令t→Tmax并注意到式(44), 得

(50)

由于p2-1>1, 故式(50)右端项是有限的.证毕.