基于干耦合横波超声换能器的钢丝长度检测及缺陷定位

肖生玉，赵仲杰，顾盛，潘永东

(1.同济大学航空航天与力学学院，上海 200092；2.昆山市建设工程质量检测中心，江苏苏州 215337)

0 引言

主缆和斜拉索分别为悬索桥和斜拉桥的关键承载构件，主要由高强镀锌钢丝制成的平行钢丝束构成。桥梁服役过程中，平行钢丝受到复杂的交变载荷作用，如风载荷与车辆载荷的耦合，不可避免地产生疲劳裂纹及断裂损伤，同时，当拉索的防腐系统被破坏后，暴露在侵蚀性环境下的钢丝会与酸雨及氯化物等产生腐蚀效应。物理和化学环境的综合作用加大了桥梁的安全隐患，有必要采用无损检测技术对钢丝的服役状况进行实时监测和定期检测[1]。

装配式建筑中预制构件之间采用浆锚连接方式，浆锚的连接质量直接决定结构的整体力学性能，其中连接节点处钢筋的插入长度是重要的安全指标之一。在预制构件的安装过程中，存在钢筋截断及偏位现象，会削减钢筋的有效插入长度，因此有必要在灌浆施工前对钢筋的插入长度进行检测[2]。

超声无损检测是有效的技术手段，其中超声导波(Ultrasonic Guided Wave,UGW)在杆状构件中表现出弱衰减及长距离传播的特性[3]。Beard等[4]对带肋钢筋进行导波模态分析，发现当波长与肋的特征尺寸的比足够大时，模态特征几乎不受肋的影响，可将带肋钢筋等效为光滑钢丝。潘永东等[5]选用2.5 MHz纵波探头研究了斜拉索锚固区钢丝损伤的高阶导波检测方法，钢丝长度及缺陷位置的预测结果具有较高精度。Li 等[6]采用UGW 技术监测钢筋混凝土结构中钢筋的腐蚀损伤演化过程，通过理论频散曲线分析了不同导波模态特性并开展了腐蚀试验，结果表明，随着损伤程度的增加，第1 个UGW 幅度先增大后减小，并能够完整反映腐蚀过程。

值得注意的是，已有研究工作常选用压电晶片或纵波换能器在涂抹了耦合剂的杆状构件底面激发超声导波。耦合剂的残留会腐蚀在役构件，同时，桥梁结构中，服役状态下的主缆和斜拉索无法拆卸，装配式建筑中，预制构件安装完成后只能穿过灌浆孔道或出浆孔道接触到钢筋的侧面，这两种工况下均无法将超声发射源放置在杆状构件的底面开展检测工作。为了提高UGW技术的适用性，本文提出了基于干耦合横波超声换能器的钢丝长度及缺陷检测方法。该方法具有非频散、易操作、高灵敏度等优点，且无需耦合剂，能在杆状构件的侧面实施检测，适用于桥梁缆索、灌浆套筒、钢绞线、砂浆筒等工程场景[7-8]。

1 理论分析

1.1 低阶导波模态分析

建立柱坐标下的无限长圆柱模型如图1所示。根据Navier方程，超声导波在圆柱中传播的运动方程[9]为

图1 柱坐标下的圆柱模型Fig.1 Cylindrical model in the cylindrical coordinates

式中：ϕ代表体积不变量；ωr,ωz,ωθ代表旋转矢量的三个分量；ur,uz,uθ代表r,z,θ方向上的位移；t为时间；λ,μ为拉梅常数。该方程满足应力边界条件时，可得到频率方程，进而能对各阶纵向、扭转及弯曲模态的理论群速度进行求解。

对于半径为R的圆柱模型，三种类典型超声导波模态纵向模态L、扭转模态T、弯曲模态F 的应力边界条件为

钢丝的材料参数如表1所示。根据表1中钢丝的材料参数进行数值求解，得到在频率范围0～100 kHz内的理论群速度频散曲线如图2所示。图2中的结果表明：低频段内仅存在低阶纵向模态L(0,1)、扭转模态T(0,1)及弯曲模态F(1,1)，且T(0,1)的理论群速度恒为3 142 m·s-1，与频率无关。

表1 钢丝的材料参数Table 1 Material parameters of steel wire

图2 钢丝中超声导波的理论群速度频散曲线Fig.2 Theoretical group velocity dispersion curves of ultrasonic guided wave in steel wire

1.2 超声导波检测原理

1.2.1 钢丝的长度检测

图3为超声导波检测钢丝长度的示意图。将干耦合横波超声换能器放置于钢丝侧面近端部，其轴向x垂直于法平面α，激振力F(F的方向为换能器激发方向)位于法平面α内，与钢丝轴向z形成夹角θ。干耦合横波超声换能器激发出的超声导波在钢丝中传播，模态成分与方向角θ及钢丝的几何尺寸有关，是各阶纵向、扭转及弯曲模态的组合。以纵向模态L(0,1)为例，声波从钢丝端部A出发，以群速度v向右传播，抵达钢丝端部B后发生反射，底面回波传回自发自收式干耦合横波超声换能器后被接收，利用底面回波的飞行时间t便可评估出钢丝长度L=vt/2。

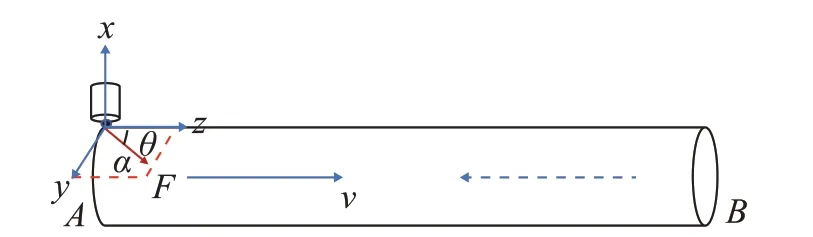
图3 干耦合横波超声换能器检测钢丝长度的示意图Fig.3 Schematic diagram of the dry-coupled ultrasonic shear wave transducer for steel wire length detection

1.2.2 钢丝的缺陷定位

超声导波与缺陷作用会产生反射及透射现象。反射回波包含缺陷的位置信息，通过解析反射回波的飞行时间及幅度变化能够实现缺陷评估。利用缺陷回波的飞行时间推算缺陷到激振源的距离：l=vt1/2，其中t1为缺陷回波的飞行时间。

2 数值模拟

2.1 钢丝有限元模型

为了探究基于干耦合横波超声换能器的钢丝长度检测的可行性，以及确定换能器的最优激发角度，采用多物理场仿真软件COMSOL Multiphysics 5.5 进行有限元数值模拟。钢丝测长及缺陷检测的有限元模型如图4所示。

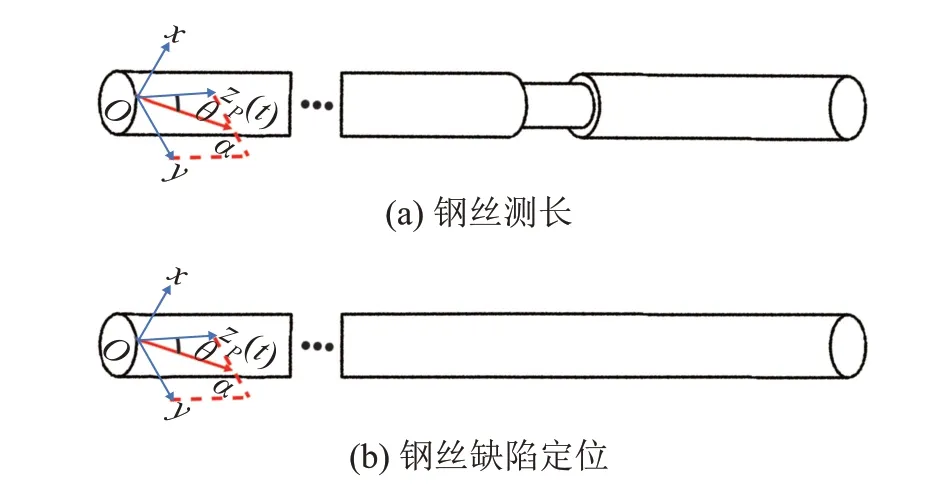
图4 钢丝测长及缺陷定位的有限元模型Fig.4 Finite element models of wire length detection and defect localization

圆柱底面半径为R，长为L。点源形式的脉冲力P(t)经汉宁窗调制后施加于圆柱侧面近端部O点。P(t)的激发方向位于法平面α内，与轴向Z形成夹角θ，数学表达式为

式中：f为工作频率，N为循环数。接收信号的采集点及接收方向分别与脉冲力P(t)的激发点及激发方向一致，即模拟了自发自收式干耦合横波超声换能器的工作原理。有限元模型的计算时间步长Δt和网格尺寸Le[10]为

式中：λmin为最小波长。钢丝的参数见表1 中，有限元仿真的各项参数值如表2所示。

表2 有限元仿真的参数Table 2 Parameters of finite element simulation

为了探究基于干耦合横波超声换能器的钢丝缺陷定位方法，在图4(b)中的有限元模型中距离O点l=2 000 mm处设置缺陷，缺陷的轴向长度为1 mm，径向深度为3 mm。

2.2 确定最优激发角度

钢丝无缺陷，激发角度θ分别为0°、45°及90°时，点O处采集的位移波形如图5所示。由图5(a)可知，波包A为初始脉冲信号，波包C、D发生部分干涉叠加，波包B、C的飞行时间分别为1 224、2 375 μs，则对应的仿真群速度分别为4 902、2 526 m·s-1。参考1.1节图2中的理论群速度频散曲线可知：频率50 kHz下的纵向模态L(0,1)、扭转模态T(0,1)及弯曲模态F(1,1)的理论群速度分别为5 033、3 142、2 559 m·s-1。比较群速度的理论值和仿真值能够确定：激发角度θ=0°时，波包B对应L(0,1)，波包C对应F(1,1)，波包D的飞行时间是波包B的两倍，对应L(0,1)的二次底面回波。同理，激发角度θ=45°时，B1～D1波包分别对应L(0,1)、T(0,1)和F(1,1)，其中F(1,1)和L(0,1)的二次底面回波发生部分干涉叠加；激发角度θ=90°时，B2、C2波包分别对应T(0,1)和F(1,1)。超声导波模态分布的仿真结果与理论一致，这也验证了有限元模型的正确性。

图5 不同激发角度θ时，点O处采集的位移波形Fig.5 Displacement waveforms at point O under different excitation angles θ

实际工况下，接收信号易受环境噪声干扰，同时钢丝中传播的超声波存在吸收衰减及散射衰减，这使得底面回波能量大幅降低，影响底面回波的识别准确度。为了让底面回波能量尽可能大，利用灵敏系数Q研究干耦合横波超声换能器的最优激发角度，其定义为

其中：Arefl为底面回波幅度，Ainc为始脉冲激励信号幅度。

图6 为不同激发角度(0°≤θ≤90°)下纵向模态L(0,1)、扭转模态T(0,1)的灵敏系数。图6 中的拟合曲线结果表明：随着激发角度的增加，L(0,1)、T(0,1)的灵敏系数皆呈现先增大后减小的变化特征，峰值分别为0.19、0.81。由于θ=75°附近的T(0,1)灵敏系数远大于θ=15°附近的L(0,1)灵敏系数，因此宜选取75°附近的激发角度。另外由图5(c)可知，当θ=90°时，L(0,1)消失，T(0,1)一次底面回波成为首波，这大大降低了导波模态和接收信号的复杂度。综上，选取90°作为干耦合横波超声换能器的最优激发角度，即换能器激发方向垂直钢丝轴向。

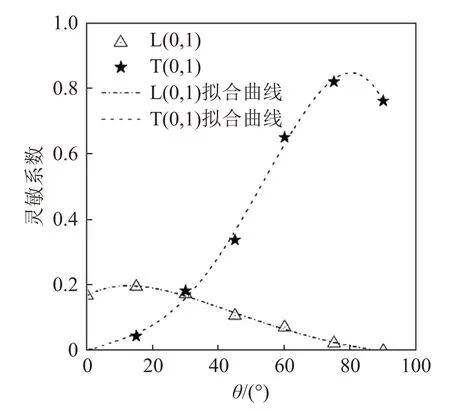
图6 不同激发角度θ时，L(0,1)、T(0,1)的灵敏系数Fig.6 The sensitivity coefficients of L(0,1)and T(0,1)under different excitation angles θ

2.3 超声导波检测的仿真结果

在最优激发角度下，由图5(c)可知，T(0,1)一次底面回波的飞行时间为1 969 μs，结合50 kHz下T(0,1)的理论群速度3 142 m·s-1可预测出钢丝长度为3 093 mm，相对误差为3.1%。由此，在理论上证实了基于干耦合横波超声换能器的钢丝长度检测的可行性。

当钢丝存在缺陷时，缺陷回波先于底面回波到达自发自收式干耦合横波超声换能器被接收到。图7为含缺陷工况下点O处采集的位移波形，B3、C3波包的飞行时间分别为1 319、1 599 μs，对应的仿真群速度分别为3 032、2 502 m·s-1，参考1.1节中的理论群速度频散曲线(图2)可知：B3波包为T(0,1)的缺陷回波，C3波包为F(1,1)的缺陷回波。结合50 kHz下T(0,1)的理论群速度3 142 m·s-1和缺陷回波的飞行时间1 319 μs 可预测出缺陷距离激发点2 072 mm，相对误差为3.6%。以上结果，在理论上验证了基于干耦合横波超声换能器的钢丝缺陷定位的可行性。

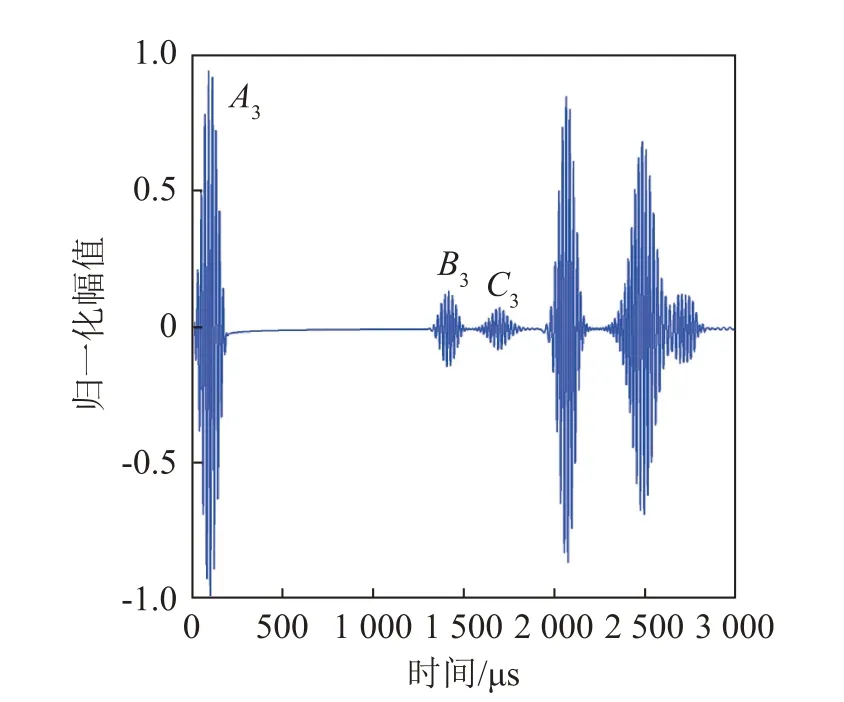
图7 含缺陷工况下，点O处采集的位移波形Fig.7 Displacement waveform at point O under defective condition

3 试验研究

3.1 超声检测系统

超声检测系统由信号发射及接收模块、50 kHz自发自收式干耦合横波超声换能器(产自德国，型号为ACS S1802)、试验钢丝、示波器及便携式电脑组成。系统组成如图8所示。换能器接收到由信号发射模块触发的电脉冲后，电能由逆压电效应转换为机械能，并以超声导波的形式辐射进入被检试验钢丝。在钢丝中传播的超声导波在端部或缺陷处会发生反射，底面回波或缺陷回波被换能器捕获并由压电效应转换为电信号，经信号接收模块放大处理后传输至示波器，最后操作便捷式电脑调取示波器展示的超声信号进行处理及分析。

图8 超声检测系统组成Fig.8 Composition of ultrasonic testing system

选定钢丝的任意端部为激发端，手持干耦合横波超声换能器垂直作用于钢丝侧面近激发端处，旋转换能器调整至最优激发角度90°，即激发方向垂直钢丝轴向。针对钢丝有无缺陷，共设置了A、B两种试件，C试件用于标定超声导波的群速度。试件尺寸如表3所示，其中缺陷位置为缺陷到激发端的距离。

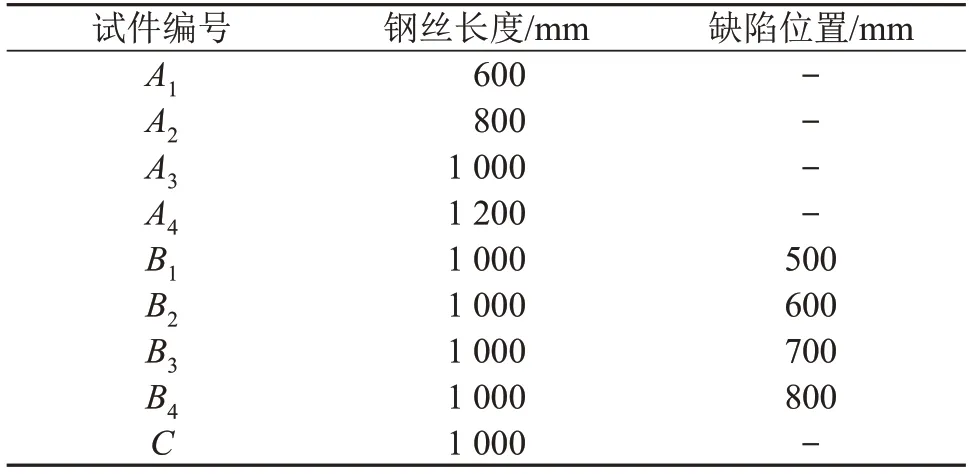
表3 试验钢丝的长度及含缺陷位置Table 3 Lengths of test wires and the locations containing defect

3.2 超声导波检测的试验结果

图9(a)、图9(b)分别为试件C和B1对应的超声信号，结果表明：试件C的底面回波表征明显，其飞行时间为622 μs，结合钢丝长度可标定出该波包的群速度为3 215 m·s-1，与理论解及仿真解吻合，由此确定干耦合横波超声换能器在钢丝中以最优激发角度激发出的导波以扭转模态T(0,1)为主。试件B1的缺陷回波飞行时间约为底面回波飞行时间的一半，且相对于无缺陷工况，有缺陷时的回波能量明显降低。

图9 检测试件C和B1得到的超声信号Fig.9 Ultrasonic signals obtained from detecting specimen C and B1

对超声信号经带通滤波及希尔伯特变换，得到距离-幅度曲线图。以试件A3和B1为例进行说明，其对应的距离-幅度曲线如图10(a)及图10(b)所示，横坐标表示导波反射位置(钢丝的端部或缺陷处)到激发端的距离。结果表明：试件A3的导波反射位置(钢丝的端部)距激发端998 mm，约等于钢丝的实际长度。试件B1的一次导波反射位置(钢丝的缺陷处)距激发端504 mm，约等于钢丝的实际缺陷位置。其他试件的预测结果如表4和表5所示，相对误差均小于2%。

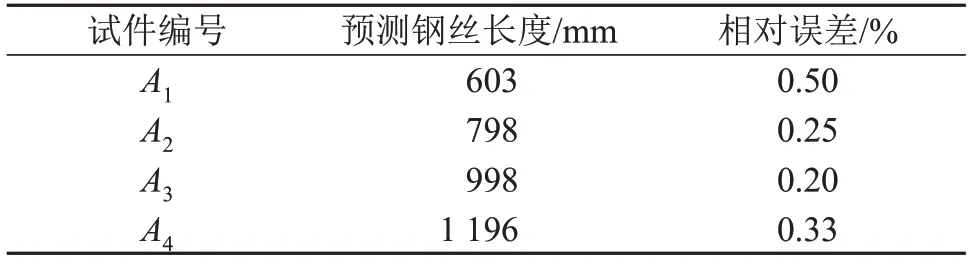
表4 试验钢丝的长度预测结果Table 4 Experimental results of steel wire length

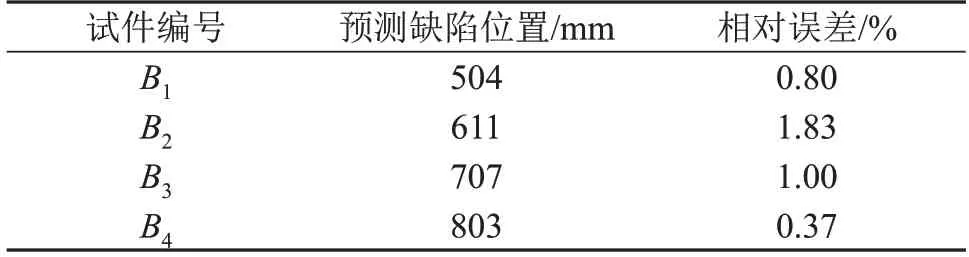
表5 试验钢丝的缺陷位置预测结果Table 5 Experimental results of steel wire defect location

图10 试件A3和B1检测信号对应的距离-幅度曲线图Fig.10 CDistance-amplitude plots corresponding to specimen A3 and B1 detection signals

4 结论

基于干耦合横波超声换能器，本文提出了在杆状钢丝侧面进行长度检测及缺陷定位的方法，得出了以下结论：

(1)建立了超声导波在钢丝中传播的有限元模型，并分析不同激发角度下超声导波的模态成分，最终确定干耦合横波超声换能器的最优激发角度为90°，即换能器激发方向垂直于钢丝轴向。

(2)提出了钢丝测长和缺陷定位的超声导波法，对于长度为3 000 mm 的钢丝，仿真结果中的钢丝长度预测相对误差为3.1%，对于带缺陷钢丝，缺陷距离钢丝端部2 000 mm，仿真结果中的缺陷位置预测相对误差为3.6%。

(3)利用频率为50 kHz干耦合横波超声换能器搭建了超声检测系统，标定了超声导波在钢丝中传播的群速度为3 215 m·s-1，并对多根不同长度和不同缺陷位置的钢丝开展长度检测和缺陷定位，试验结果中的预测相对误差均小于2%。