基于连续谱特征的被动声呐跟踪方法
2024-01-17王卓然王鲁军谢亮王佳囡
王卓然,王鲁军,谢亮,王佳囡
(1.声纳技术重点实验室,浙江杭州 310012;2.杭州应用声学研究所,浙江杭州 310012;3.中国船舶集团有限公司军工部,上海 200011)
0 引言
被动声呐目标跟踪是利用多波束测量信息对目标的方位和运动状态进行估计预测的过程,在战场指挥决策以及定位、识别等处理中发挥着重要作用。常规的极大值跟踪方法通过划定搜索窗长,搜索窗内能量的最大值所对应波束为下一时刻的预测波束。这种方法简单,适用范围广,但是对于目标的信噪比和轨迹的连续性要求较高,稳健性差。考虑目标方位随时间的变化特性,研究人员提出了一些基于目标运动特性的跟踪算法。贝叶斯理论的滤波方法在被动跟踪领域中的广泛应用,在线性系统假设下,卡尔曼滤波算法(Kalman Filter,KF)[1]表现出最优的跟踪性能,但是对于非线性、非高斯系统,卡尔曼滤波算法性能下降。为了提升非线性场景下的跟踪性能,研究人员又提出了扩展卡尔曼滤波[2-3]和无迹卡尔曼滤波,粒子滤波[4-6]等算法。这些算法依靠建立目标运动模型和量测模型,通过贝叶斯滤波对目标状态的后验概率密度进行估计进而求出目标的运动状态。
最邻近关联、联合概率互联(Joint Probabilistic Data Association,JPDA)[7]、多假设跟踪(Multiple Hypothesis Tracking,MHT)[8]等算法通过与滤波算法结合实现了目标的跟踪与关联,然而这些方法仅利用了目标的运动信息,在解决目标长时间交叉的情况下关联分辨效果不佳。邱伟等[9]使用线谱特征作为辅助信息对概率数据关联滤波(Probability Data Association,PDA)算法进行了改进,提高了跟踪性能,但是该方法仅能在目标具有明显线谱特征情况下使用。钱宇宁等[10]提出了一种利用历史运动特征和支持向量机(Support Vector Machine,SVM)进行频谱分类进而实现目标关联的跟踪方法,该方法虽然能解决目标交叉跟踪的问题,但其实现目标关联需要依靠样本进行学习,在一定程度上增加了运算量以及算法的复杂度。
现有基于频谱特征的跟踪方法大都使用线谱作为主要特征,而连续谱作为表征连续谱宽带结构的重要组成部分,已用于目标的识别[11],在跟踪领域的使用较少。同时,现有的算法大多假设目标的特征表现稳定,而较少考虑到环境和目标工况对特征谱的影响和变化。本文提出了一种基于连续谱特征的被动目标跟踪方法,构建了连续谱特征表征方式以及相似匹配方法,使用动态更新特征谱实现了目标的长时间交叉关联跟踪。
1 基本原理
在多目标跟踪过程中,当测量点相距较近而难以分辨时,特征辅助方法利用测量的特征量与已有的目标特征进行匹配,可以实现测量与目标的关联。为了能够获得稳定、准确的关联效果,特征辅助算法要求选取的特征具有稳定持久,可分性强的特点。
在被动跟踪和识别领域,目前被广泛使用的特征主要来自于目标辐射信号的频谱[10]。目标舰船在航行过程中辐射的噪声由水动力噪声、机械噪声以及螺旋桨噪声构成,其中占据主导地位的是螺旋桨噪声和机械噪声。舰船辐射噪声可以描述为连续谱和线谱的叠加。连续谱主要来自于目标的螺旋桨噪声,由目标空化现象或螺旋桨机械振动产生,在频谱上表现为宽带信号。线谱主要来自于目标机械部件的振动,在频域上表现为离散的窄带信号。现有的算法大多选取线谱作为特征量,然而在实际情况中通常会遇到目标不表现出线谱特征或线谱比较微弱难以提取的情况。连续谱作为功率谱中的宽带特征量,决定了功率谱的形状结构,包含了丰富的目标特征信息,可以作为目标跟踪和分辨的特征量。各个波束对应的功率谱P可表示为
式中:Pi(f)对应第i个波束的功率谱,其中i=1 2…,m,m为波束个数。目标波束s对应的功率谱Ps(f)可以表示为目标舰船辐射噪声功率谱S(f)与海洋环境噪声N(f)的叠加,而未出现目标的波束b对应的功率谱可表示为海洋环境噪声N(f),表达式分别为
受到目标舰船辐射噪声的影响,目标方向上的谱与目标未出现方向上的谱存在差异,对于同一目标发出的舰船辐射噪声,这种特征具有相似性[11]。由于不同目标的舰艇类型,航行速度、工况、机械结构等存在着差异,其对应的功率谱与背景噪声的差异也有所不同。在目标航迹交叉前后,同一目标对应的功率谱将保持相似的特征。因此目标功率谱的结构特征具备稳定且可分的特点,可以作为特征量用于跟踪。
目标功率谱的结构特征主要由连续谱和线谱共同构成。连续谱决定了目标功率谱的宽带结构,提取出连续谱的方法一般有折线法[12]、拟合法[11,13]、频带能量法[12]等。折线法主要通过提取连续谱的谱峰频率、低频上升斜率和高频下降斜率来对连续谱的基本形状进行描述。这种连续谱提取方式较为粗糙,会导致连续谱信息的丢失。拟合法是使用例如Savitzky-Golay 滤波器、双向α滤波等平滑算法对功率谱滤波以实现连续谱形状的提取。这种提取方式对连续谱的形状有较高的拟合精度,但是完全剔除了线谱的影响,不利于从整体上考虑目标的功率谱结构。频带能量法通过将功率谱划分成为若干子带,通过计算各子带的能量构建向量以实现连续谱结构特征的提取。这种方法综合考虑了目标的线谱和连续谱对功率谱结构的影响,因此本文将使用频带能量法作为连续谱特征的提取方法。
2 基于连续谱特征的目标跟踪方法
由第1节可知,目标的连续谱在频域上具有较稳定的特征,在交叉过程中仍能保持稳定,可以通过在局部搜索窗内与目标特征谱最为相似的波束作为跟踪波束来实现跟踪。因此本文利用连续谱特征作为特征量,提出一种基于连续谱特征的被动目标跟踪方法。本文所提方法的跟踪流程如图1所示,主要由特征谱表征模块、特征匹配模块、交叉判断模块、特征谱更新模块构成。

图1 基于连续谱特征的被动目标跟踪方法流程图Fig.1 Flowchart of passive target tracking method based on continuous spectrum features
2.1 连续谱特征的表征
为了提高宽带连续谱结构特征的显示性能,降低向量长度,本文使用频带能量法对各波束的频谱进行处理。设声呐工作的频率范围为[fmin,fmax],波束数为M,将其等间隔划分为n个频带,得到:L=[L1(u)L2(u)…Lm(u)],其中u=1,2,…,n,为频带序号,m=1,2,…,M,为波束序号,对于Li(u),设其第u个子频带的带宽为[fu,min,fu,max],则有:
选取的子频带的带宽会影响到连续谱结构的表征能力以及运算量。过宽的子频带会导致连续谱结构特征信息的丢失,而过窄的子频带则会增大运算量,一般将子带带宽选择为20~40 Hz。经分频段处理后,宽带连续谱特征被集中显示,并且频带内的线谱特征也可以通过Li(u)进行表征。Li(u)包含了背景噪声成分,为了降低背景噪声对目标信号特征的影响,提取出较为稳定的谱结构特征,需要对每时刻的背景噪声进行估计。本文使用排序截断平均(Order Truncate Average,OTA)算法[14]对目标各个频点周围的背景进行估计。经OTA 算法处理后,得到各波束的背景谱估计为
其中:Lbi(u)表示第i个波束使用OTA算法计算的得到的背景谱在第u频段上的取值。使用各波束的原始谱L减去估计的背景谱LB,并将小于0的值置为0,得到去背景谱LC=[Lc1(u)Lc2(u)…Lcm(u)]。
对于目标出现的波束s,其去背景谱Lcs会在具有连续谱特征的频段上表现出较大的谱值并且具备一定的形状,而不含目标特征频段的谱值将接近于0。为了进一步提升目标特征在波束域上的集中性,对Lc的各频段进行峰值提取,得到经过峰值提取处理的特征谱Lp:
根据目标峰值分布的空间一致性,在经过峰值提取后得到的特征谱将会在目标波束处出现大量的峰值。峰值的个数,位置以及幅度反映了该目标的特征,可以用来进行目标的关联与跟踪。
2.2 相似度计算方法
计算得到各波束的特征谱后,需要根据目标的跟踪位置划定搜索窗,选择窗内特征谱与跟踪目标特征谱最为相似的波束作为本时刻的跟踪方位。
定义特征谱Lpt(u),其表征了跟踪目标的特征,与目标特征谱做相似度运算的谱为待比较谱,记为Lpc(u)。将目标特征谱Lpt(u)中值为0的频段记为F0,将待比较谱Lpc(u)中的对应频段置为0,得到投影谱L'pc(u)。计算Lpt(u)和L'pc(u)的广义杰卡德(Jaccard)系数V:
由于信号的能量大小也是其特征的一种表示,考虑引入能量作为辅助特征量,计算待比较两个谱的能量相似比对V进行加权:
为了便于描述,后续把上述计算Lpc(u)和Lpt(u)相似度的过程表示为Vw=sim(Lpc,Lpt)。
2.3 特征谱更新
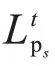
(1)当目标未开始交叉时,每次更新目标方位之后,将目标特征谱更新为当前方位对应的特征谱。
(2)当目标进入交叉后,计算关联特征谱Lpst并保存,依据特征谱各频点谱值的统计特性,选取关联特征谱Lpst为到t时刻为止未交叉状态所有目标特征谱的平均。同时按式(9)将目标特征谱更新为当前方位对应的特征谱。
(3)当目标结束交叉时,将目标特征谱替换为保存的关联特征谱Lpst:
在判断为结束交叉之后,目标从交叉状态变为分离状态,此时将目标特征谱更新为Lpst,即可完成交叉目标的关联。
2.4 目标状态判定
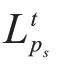
图3表示目标未进入交叉的状态时,其部分特征泄漏至相邻的波束,在这种情况下存在:
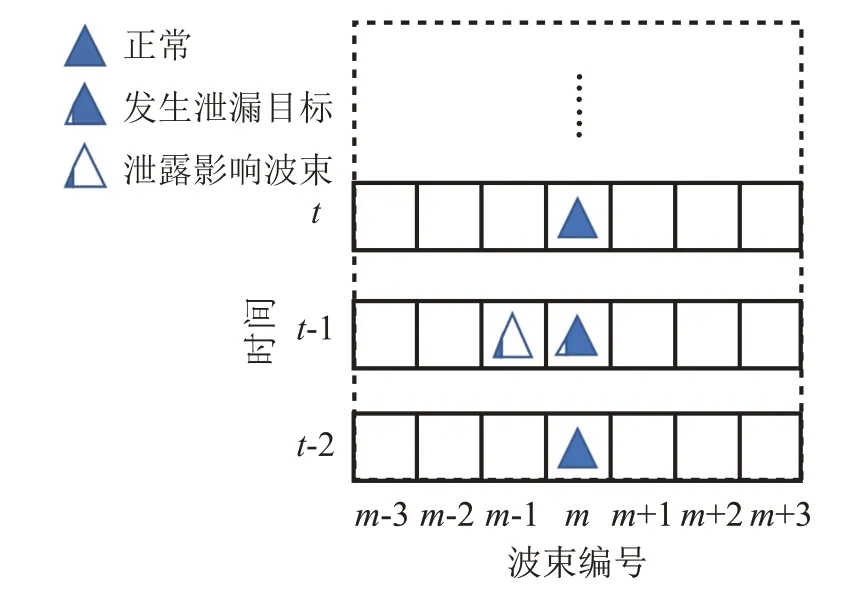
图3 目标特征泄露示意图Fig.3 Schematic diagram of target feature leakage
其中:ε为阶跃函数,表达式为
式中:T1为设定的0~1之间的门限值,T1的选取与交叉前后目标特征谱的变化程度有关,对于未处于交叉状态的目标,其前后帧特征谱的相似度一般大于0.2,通常选取0.2作为交叉判决门限。在判定为交叉之后,对交叉前所有目标特征谱进行平均并保存,得到保存关联特征谱Lpst。在目标进入交叉之后,需要按照交叉后叠加的特征谱进行匹配跟踪,同时使用Lpst对当前跟踪波束的左右K2个波束进行相似度计算,得到:
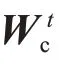
设定T2为重新关联门限值,T2的选取与目标特征谱的相似度有关,因此重新关联门限值T2可以依据T1的值进行设置。结束交叉状态的判断条件为
综上所述,基于连续谱特征的被动目标跟踪算法的具体步骤为:
(1)设定基本参数,基本参数包括:目标跟踪搜索窗长K,交叉重新关联搜索窗长K2,频谱划分的段数n,交叉判决门限T1,交叉重新关联门限T2,目标初始方位θ0。
(2)按照2.1节的特征提取方式计算得到各方位对应的特征向量Lpi(u)。
(3)对当前搜索窗内的特征向量与目标特征谱进行相似度匹配计算,得到相似度向量:
(4)计算交叉判别指标,按照式(13)、(18)进行目标轨迹状态判断。
(5)根据步骤(4)得到的目标状态,按照2.3节所述进行特征谱更新,输出当前时刻更新的目标跟踪结果,重复步骤(2)~(5)。
3 仿真实验分析
假设等间隔布阵的均匀线阵的阵元数为64,阵元间距为1.2 m,采样率为5 kHz,工作带宽为200~800 Hz。设置三个交叉远场目标,目标1初始方位为48°,目标辐射信号的连续谱在500 Hz处出现谱峰,信噪比为-20 B;目标2初始方位为61°,辐射信号的连续谱在600 Hz表现出谱峰,信噪比为-18 dB;目标3 初始方位为77°,辐射信号的连续谱在300 Hz出现谱峰,信噪比为-12 dB。
图4所示为目标1~3的频谱。目标1和目标3在15 s处长时间交叉,保持交叉15 s后彼此分离,目标2与目标3在第6 s交叉。
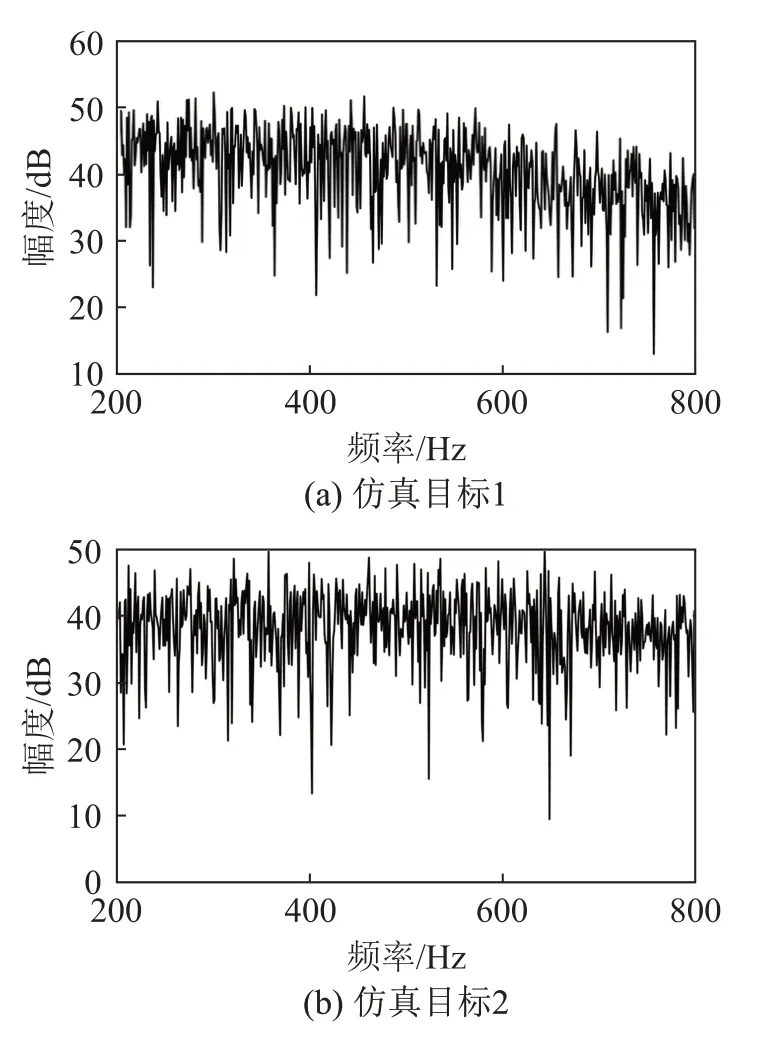
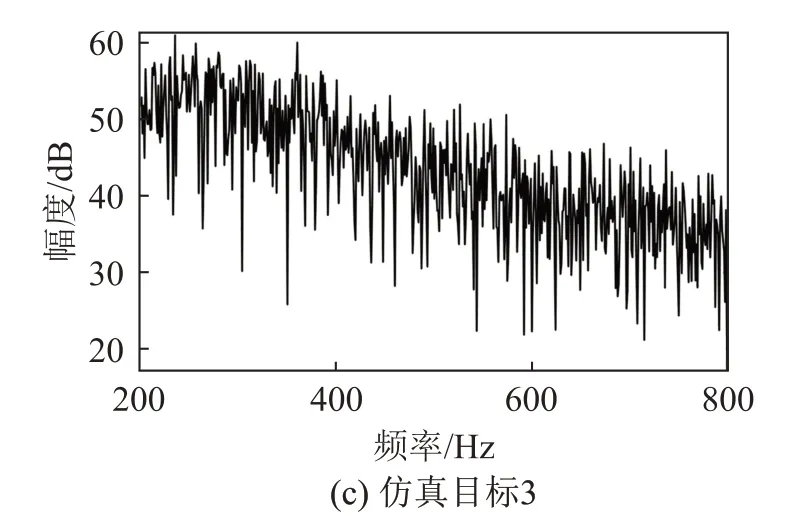
图4 仿真目标的频谱Fig.4 Spectrums of simulated targets
图5为使用频带能量法提取出的各波束宽带能量谱以及使用OTA 方法估计出的该波束位置对应的背景谱。图5(a)~5(c)为目标1~3宽带能量谱与背景谱,可以看出,目标谱均高于背景谱,并且不同的目标其高于背景谱部分的形状也各不相同,表现出了各目标连续谱的特征。图5(d)为未出现目标波束的频带能量谱和背景谱,可以看出其频带能量谱与背景谱基本重合。

图5 各波束宽带能量谱及对应的背景谱Fig.5 Broadband energy spectrum of each beam and the corresponding background spectrum
图6所示为使用本文方法处理,经过谱特征表征过后,得到的三个目标特征谱,采用20Hz 为带宽进行频带划分,可见三个目标的特征谱各自表现出特征,可以用相似度匹配方式来彼此区分,实现交叉关联。
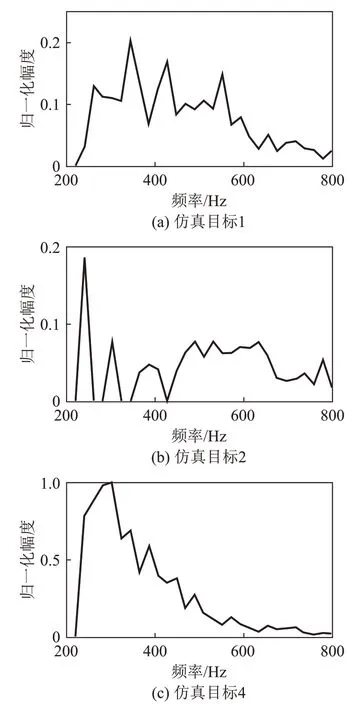
图6 仿真目标的特征谱Fig.6 Characteristic spectrums of simulated targets
仿真生成的数据经过常规能量检测过后,将方位历程数据作为输入,分别使用粒子滤波(Particle Filtering,PF)[4]和KF+JPDA 关联处理的方法进行跟踪。PF 方法是一种检测前跟踪的方法,使用方位历程作为输入,具有避免关联,适应低信噪比跟踪的特点。KF 是一种常规的跟踪算法,使用过阈值的能量检测结果作为输入,JPDA算法是一种经典的测量关联算法,通过计算匹配概率矩阵来对航迹和测量进行关联,通过使用JPDA 联合KF 滤波解决交叉目标场景下的跟踪问题。使用以上两种算法跟踪,得到的跟踪结果如图7(a)、7(b)所示,本文跟踪方法处理得到的结果如图7(c)所示。

图7 不同跟踪算法的跟踪结果Fig.7 Tracking results of different tracking algorithms
表1为采用不同算法对三个目标交叉位置的跟踪关联结果。PF算法和KF+JPDA算法均能够正确关联目标2 和目标3 航迹在第10 s 处的短时交叉,但是无法对目标1和目标3的长时间交叉精确跟踪。PF 算法由于在交叉区域保持长时间相同的似然函数,导致目标1和目标3的粒子权重趋同,从而造成在目标结束交叉的时候两目标的跟踪方位趋于一致。由于目标1和目标3的轨迹在交叉处完全重合,而JPDA算法只允许单个目标关联单个测量,因此在二者交叉过程中,目标3能够正常跟踪,而目标1始终无法与测量关联,导致其跟踪位置偏离正确方位。使用本文的方法能够依据不同目标的连续谱特性,对目标的交叉状态进行判断,动态地选取匹配目标特征谱,实现了目标在长时间交叉航迹分裂后的重新关联,能够有效解决多目标交叉情景下的跟踪问题。
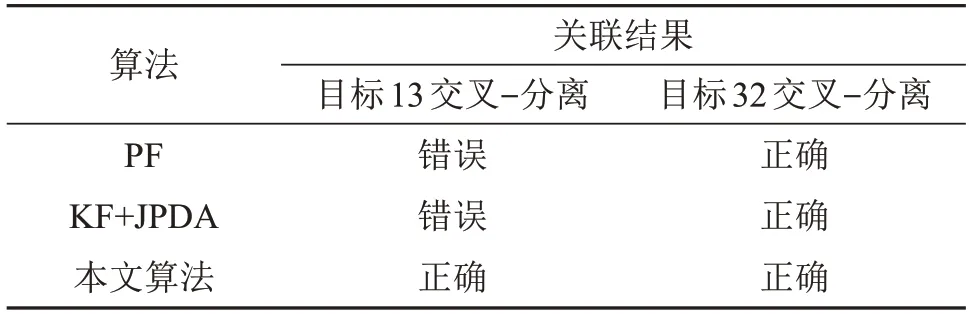
表1 目标交叉关联结果Table 1 Result of target crossing correlation
表2和表3分别为仿真的三个目标在交叉之前以及全程的跟踪误差比较。跟踪误差为观测时间内,跟踪算法输出方位估计值和真值的均方根误差。由表2可知,当目标未表现出交叉时,三种算法对三个目标的跟踪误差均小于1°。本文所提算法的跟踪误差均小于0.5°,表现出比其他方法更高的跟踪精度。由表3可知,考虑目标的交叉,由于存在错误关联的情况,使用PF 和KF+JPDA 算法对目标1的跟踪误差较大;对于目标2的跟踪,三种算法的跟踪误差均小于0.5°,其中PF的跟踪精度要略高于本文算法的精度。由于目标3的运动轨迹并非直线运动,而本文仿真采用的PF 方法和KF+JPDA方法均基于直线运动建立运动模型,两种方法对于目标3的跟踪发生了模型失配,因此跟踪精度均低于本文所提算法的跟踪精度。
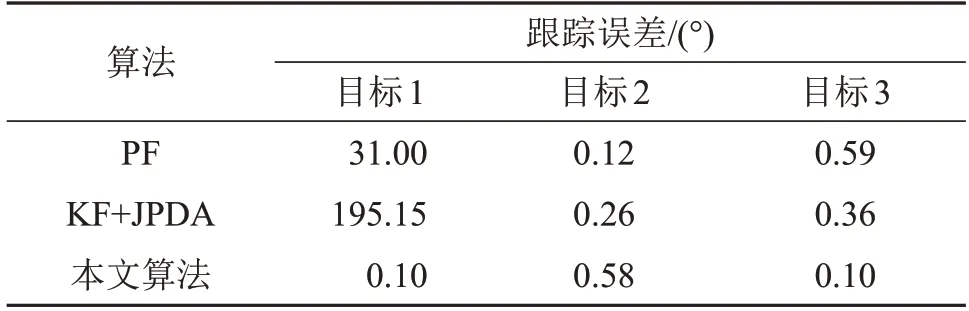
表3 目标全过程跟踪误差比较Table 3 Comparison of tracking errors in the entire target process
为了比较各方法运算速度,本文计算了各方法处理单帧数据的运算时间,结果如表4所示。由表4可以看出,基于蒙特卡洛(Monte Carlo)的PF方法由于需要使用大量的粒子对目标状态的后验概率密度进行估计,其运算时间较长。KF+JPDA 方法的运算量主要来自于互联矩阵以及关联概率的计算,当目标数目和量测数目增加时,其计算量会显著增大。本文所提的基于连续谱特征的被动声呐跟踪方法的运算量主要来自于特征谱表征以及相似度的计算,在仿真实验中其运算时间略小于KF+JPDA 方法的运算时间。

表4 各算法单帧运算时间比较Table 4 Comparison of single frame operation time of various algorithms
4 海试数据分析
为了验证基于连续谱特征的目标跟踪方法的有效性,利用某段海试验数据进行分析,接收处理带宽为200~1 000 Hz。图8(a)为海试数据的方位历程图。从图8(a)可以看出,起始位置位于120°附近的两个目标在该段时间内存在交叉-分离-交叉-分离的复杂运动态势,图8(a)中标注的交叉1、交叉2、交叉3为其中关键的交叉位置。起始位置为145°的目标则与右侧两个目标分别交叉,出现了交叉4、交叉5的交叉位置。使用不同的算法分别对这5个目标进行跟踪处理,图8(b),8(c),8(d)分别为使用PF,KF+JPDA 跟踪算法以及本文所提算法得到的跟踪结果,不同目标的跟踪轨迹使用不同的线形和颜色加以区分。

图8 海试数据时间方位历程图及不同跟踪算法的跟踪结果Fig.8 Time-azimuth history charts and tracking results with different algorithms of sea trial data
表5中记录了不同算法对海试数据中目标的跟踪关联结果。从表5中可以看出,PF方法对交叉2、交叉3以及交叉5的跟踪出现了错误关联。这是因为粒子滤波算法采用能量值作为似然函数的输入,当存在一强一弱目标交叉且交叉时间较长时,粒子的权值受到能量较大目标的影响,导致位置的估计偏向强目标,最终造成跟踪错误。使用KF+JPDA算法在交叉2和交叉3处出现了跟踪错误。这是由于在交叉2处的弱目标受到强目标的遮蔽作用,其表现为峰值的有效量测未能落入关联门内,从而导致了跟踪错误;由于无法正确处理交叉2,在交叉3处两目标的跟踪状态基本一致,对于出现的两个有效量测,二者只对其中一个符合运动状态模型的量测进行争夺,最终导致了跟踪交叉3的跟踪关联错误。

表5 海试数据目标交叉关联结果Table 5 Results of target crossing correlation of sea trial data
根据图8(d)以及表5所示,使用本文提出的基于连续谱特征的被动目标跟踪方法的跟踪能够正确处理海试数据中的五个交叉问题,通过特征谱对每个目标的连续谱特征进行表征,选择与跟踪目标特征谱最为相似的波束作为跟踪波束,实现了对各个目标的有效跟踪。本文所提算法使用交叉状态判断以及特征谱更新策略,能够有效解决目标的交叉-分离关联问题,由于不需要事先假设运动模型,对于较为复杂的目标运动轨迹能够表现出较好的适应性。
5 结论
本文提出了一种基于连续谱特征的目标跟踪方法。该算法利用目标信号连续谱特征稳定的特性,通过利用频带能量法结合OTA 及峰值提取算法提取出目标连续谱的特征向量,采用特征相似度匹配的方法实现了交叉目标的有效跟踪。本文通过仿真对比分析了该方法的跟踪性能,并利用海上试验数据验证了算法对多目标跟踪的有效性。本文通过研究得到以下结论:
(1)目标具有较为稳定的连续谱特征,可以作为辅助特征用于被动目标跟踪,提取出的连续谱特征结合目标特征谱更新策略能够在目标长时间交叉后依旧保持较高的相似性。
(2)根据仿真和实测数据结果,与PF 算法和KF+JPDA 算法相比,在目标航迹交叉的条件下,本文算法能够有效对目标进行关联跟踪,跟踪精度较高,具备解决多目标长时间交叉跟踪的能力。
(3)本方法不需要构建运动模型,能够用于具有较为复杂航迹的跟踪,其计算量相比PF 方法以及机器学习类算法较小,并且不会随着目标和测量的增多发生计算量的急剧升高,能够满足实时性要求,物理过程清晰。
