Pekeris波导环境中的水下运动声场仿真研究

姚舟磊，于晓林，许伟杰

(1.中国科学院声学研究所东海研究站，上海 201815；2.中国科学院大学，北京 100049)

0 引言

Pekeris 波导是Pekeris 提出的由一个均匀海水层和一个液体半无限空间组成的波导环境[1]。Pe‐keris波导可以看作是浅海环境的一个合理的简化模型，研究该模型中的声传播问题具有重要的理论和实际意义[2-3]。

波数积分方法是声场建模的主要方法之一，适用于水平分层的波导环境。Pekeris[1]在1948年首次将波数积分方法引入到水声学中，利用波数积分方法来处理Pekeris波导中的声传播问题。骆文于等[4]通过合理的归一化，提出了一种数值稳定的波数积分方法。

国内学者对水下静止声源的声场已有较多的研究[5-7]，但对运动声源的声场研究较少。如今鱼雷等水下武器装备的运动速度能达到80 m∙s-1[8]，这对水下目标跟踪提出了更高的要求。对水下运动声源的声场研究能为声呐测速和测距提供理论基础，具有现实意义。国外对水下运动声源的声场特性研究已有不少成果，但多数是用简正波方法[9-10]和射线方法[11]进行分析。Schmidt 等[12]给出了水平不变环境中声源和接收器联合运动时的波数积分和简正波表达式，并用修改的SAFARI模型进行仿真。

本文对Pekeris 波导中的运动声源声场进行分析，给出运动声源二维波数积分的一维近似表示，并利用文献[4]提出的数值稳定波数积分方法对声场进行求解。首先在自由空间验证了近似的一维波数积分表示的准确性，再分析Pekeris 波导中运动声源的声场特性。

1 理论推导

1.1 Pekeris波导中运动声源的波数积分解

Pekeris波导环境示意图如图1所示，海水的密度和声速为ρ1,c1,海水深度为D，海底的密度和声速为ρ2,c2。声源为单频点源，以速度vs匀速运动。由于声源的运动会破坏柱面的对称性，因此引入笛卡尔坐标系。

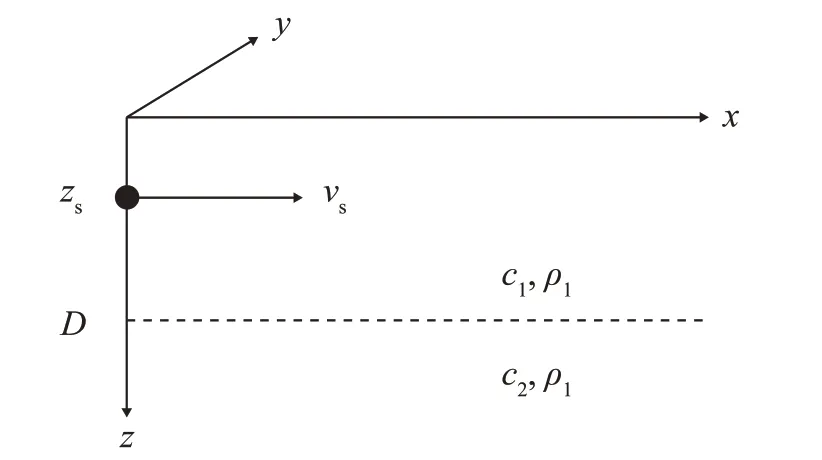
图1 Pekeris波导环境示意图Fig.1 Schematic diagram of Pekeris waveguide environment

为了计算方便，令x-y平面为海平面且x轴正方向为声源运动方向，在t=0时刻声源正处于z轴，位置记为(0,0,zs)。该声源满足如下的波动方程[9]：

式中：ψ表示t时刻的声压，Ω为声源的圆频率，δ函数为狄拉克函数。利用傅里叶变换对：

可以得到运动点源波动方程对应的亥姆霍兹(Helmholtz)方程：

式中：k=ω/c，是频率ω对应的波数。

使用二维空间傅里叶变换可将Helmholtz 方程在空间-波数域上进行转换，其中x域的傅里叶变换对为

对式(4)进行空间傅里叶变换可将x域转换到kr波数域：

利用δ函数的性质可对式(7)进行化简，可以得到：

再将式(8)从y域变换到ky域可得：

式(9)是三维笛卡尔坐标系下运动点源深度分离的波动方程，其解的表达式为

其中：G(kx,ky,z,ω)是频率为ω时的深度格林函数。对式(10)进行傅里叶逆变换就能得到声场的时域解：

将式(11)代入式(10)并化简，可得：

式(12)为运动点源声场的二维波数积分解。式(12)中的双重积分一般只能通过数值方法求解，而在远场的情况下，为了提高解的精度需要增大水平波数kx、ky的采样数量，但会大大增加运算时间。

因此在远场条件下，假设声源与接收器都位于x-z平面，且声源与接收器的水平距离远大于垂直距离，可认为声源与接收器距离是匀速变化的。利用稳相法[16]可将式(12)的二维波数积分解近似为远场条件下的一维波数积分：

式中：Ω±kxvs表示声源运动产生的多普勒频移对深度格林函数造成的影响，当声源靠近接收器时多普勒频移大于0，符号为正；相反当声源远离接收器时取负号。式中R(t)=R0∓vst为t时刻时声源与接收器的水平距离，R0为t=0时声源与接收器的初始水平距离，当声源接近接收器时取负号，声源远离接收器时取正号。

1.2 数值稳定格林函数的表示

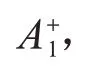
在之前的研究中，文献[13]和文献[14]给出了两种Pekeris 波导中点源声场的深度分离格林函数表达式：

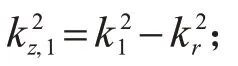
文献[4]指出，式(17)和式(18)理论上是正确的，但是在求解待定系数矩阵方程时，由于上下行波选取的参考点不合理，导致在实际仿真中系数矩阵容易产生数值溢出的情况，会使求解得到的深度格林函数不稳定。文献[4]通过合理的归一化，将深度格林函数表示为

代入边界条件(14)～(16)，可得线性方程组：

通过求解式(20)中的方程组，可得到Pekeris波导中数值稳定的深度格林函数，在计算过程中再将频率替换成由声源运动所产生的多普勒频移Ω±kxvs并代入式(13)，便可得到运动声源数值稳定的一维时域波数积分近似解。

2 仿真算例

第1 节给出了运动点源声场的二维波数积分解。但由于二维解的计算量较大，因此在远场情况下引入一定的假设，将解近似为一维波数积分解。本节先模拟自由空间下运动点源的声场，通过对比远场条件下的一维波数积分解与解析解，来验证式(13)的准确性；再根据式(13)和式(20)的方程组对Pekeris 波导环境下的水下运动声源的声场进行研究。

2.1 运动声源声场一维波数积分数值解的验证

自由空间中单频运动点源所产生的声场存在解析解。假设点源频率为f0，以速度v沿x轴匀速运动，t=0时刻位于原点，则声场解析解为[15]

其中：

式中：M为声源运动速度v与介质声速c的比v/c。

模拟自由空间参数如下：空间的介质声速为1 500 m∙s-1，介质密度为1 000 kg∙m-3,运动点源的频率为100 Hz，从原点(0,0,0)开始沿x轴正方向、以100 m∙s-1速度匀速运动，接收器坐标为(10 000,0,50)。

图2(a)、图2(b)、图2(c)分别是在0、20、40 s时计算解析解和数值解得到的声压幅值，对应的是声源与接收器距离10、8和6 km的时刻。图2(d)是0～80 s接收器接收声压级的变化曲线。图2(d)中解析解与数值解得到的声压级变化曲线吻合，误差为0.3 dB左右。图2中蓝色实线是解析解，黄点是式(13)计算的数值解。可以看出在自由空间中，声源与接收器相距较远的远场条件下，一维波数积分数值解和解析解的计算结果符合的比较好。

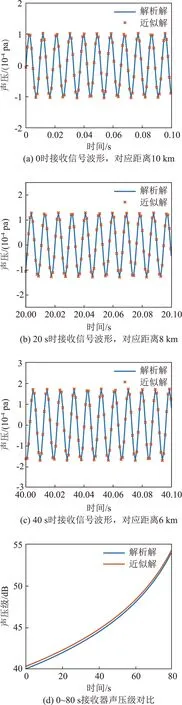
图2 不同时刻的接收波形和接收声压级的解析解与数值解对比Fig.2 Comparison between analytical and numerical solutions of the received waveforms and sound pressure levels at different times

因此，在远场条件下，一维波数积分的数值解的精度较高，能满足运动声源声场的计算。在自由空间下运动声源多普勒频移的理论值为

式中：f0为声源的频率，θ(t)为t时刻声源、接收器连线方向与声源运动方向的夹角。当水平距离远大于垂直距离时可忽略角度θ的影响，计算得到距离较远时的多普勒频移理论值为107.14 Hz。图3对比了0～99 s接收信号解析解、近似解的瞬时频率和上式计算得到的多普勒频移理论值，可以看到接收信号的瞬时频率与理论值吻合较好。

图3 信号瞬时频率解析解、近似解和理论值的对比Fig.3 Comparison of the analytical and approximate solutions of signal instantaneous frequency and the theoretical values

2.2 Pekeris波导运动声源数值稳定解的仿真

将Pekeris 波导中数值稳定深度格林函数代入式(13)，并进行数值仿真。Pekeris波导仿真环境如图4所示，其中海水声速为1 500 m∙s-1，密度为1 000 kg∙m-3，海深为100 m，海底声速为1 800 m∙s-1，密度为1 800 kg∙m-3，海底的吸收系数为0.2 dB∙λ-1。在初始时刻声源位于z轴，深度为36 m，坐标为(0,0,36)。声源频率为50 Hz，以100 m∙s-1速度沿x轴正方向运动。接收器深度为46 m，与声源水平距离10 000 m，坐标为(10 000,0,46)。

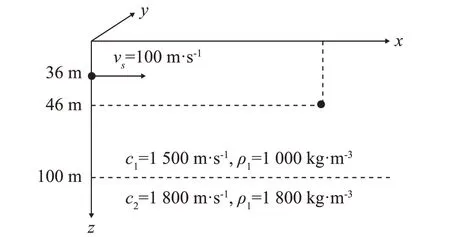
图4 Pekeris波导环境的仿真Fig.4 Simulation of Pekeris waveguide environment

当声源静止时，直接求解式(20)中的方程组得到该波导环境下静止声源的深度格林函数的幅度，结果如图5所示。用KRAKENC声场仿真软件仿真该波导环境，计算得到该波导环境共会产生4阶简正波。表1 是图5 的4 个峰值幅度对应的波数kx与KRAKENC求解得到的各阶简正波水平波数值。表1显示该波导环境下静止声源的深度格林函数峰值对应的波数与各阶简正波的水平波数相符合。

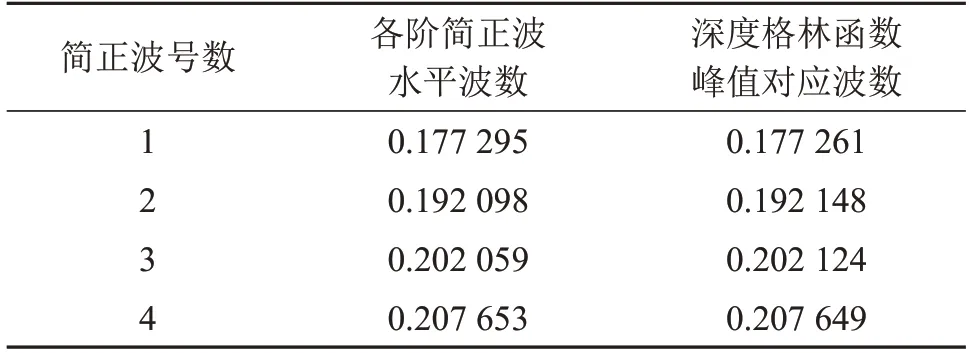
表1 各阶简正波水平波数与深度格林函数峰值对应波数对比Table 1 Comparison of the horizontal wavenumber of each order of normal waves and the corresponding peak wavenumber of depth Green's function

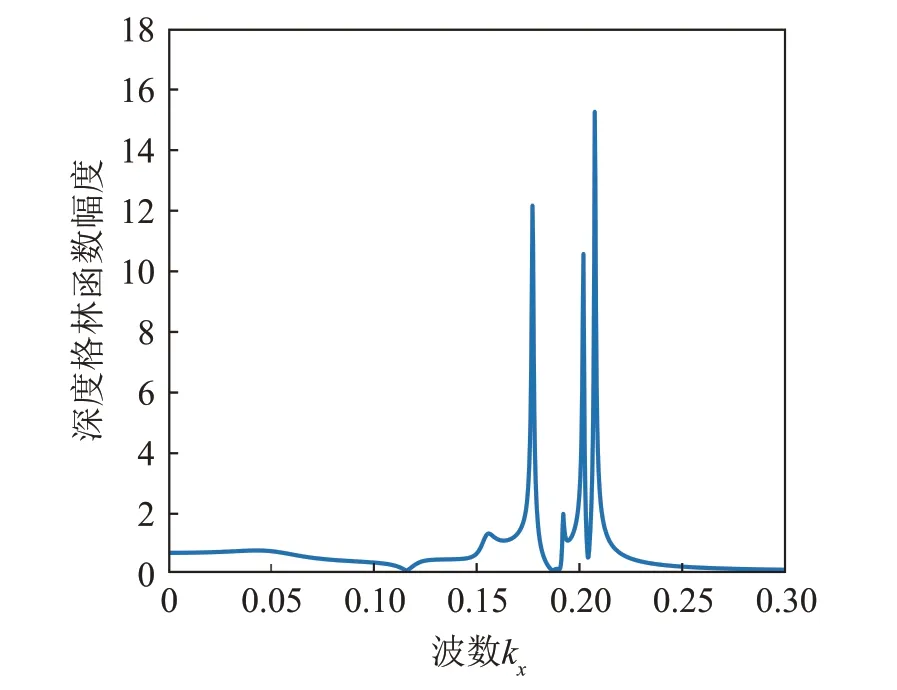
图5 静止声源的深度格林函数幅度Fig.5 The amplitudes of the depth Green's function for the stationary sound source

当声源运动时，深度格林函数需要加上多普勒频移，即式(13)中的Ω±kxvs，当声源靠近接收器时取负号，远离接收器时取正号。图6是该波导环境下声源不同运动状态时深度格林函数的幅值，其中实线是声源静止时的深度格林函数的幅值，虚线是声源以100 m∙s-1速度远离接收器时深度格林函数的幅值，点划线是以100 m∙s-1速度接近接收器时深度格林函数的幅值。由图6可以看出，当声源接近接收器时多普勒频移使深度格林函数峰值对应的波数增大；声源远离接收器时深度格林函数的峰值波数减小。

图6 声源不同运动状态时深度格林函数的幅度Fig.6 Amplitudes of the depth Green's function under different motion states of a sound source

求解式(13)得到时间区间为0～80 s时接收声压信号的波形，结果如图7所示。其中蓝线是声源静止时的接收信号波形，红线是声源以100 m∙s-1速度匀速靠近接收器时接收的信号。

图7 在0～80 s时间内的接收波形Fig.7 The received waveform from 0 to 80 s

图8(a)～8(c)分别对应0、20、40 s时刻接收器的声压时域波形。由图8可以看出，由于声源与接收器水平距离随时间发生变化，接收声压的幅度会发生起伏，并随着声源的接近幅度增大。由于声源向接收器运动产生多普勒频移，接收信号的频率大于声源静止时接收信号的频率。

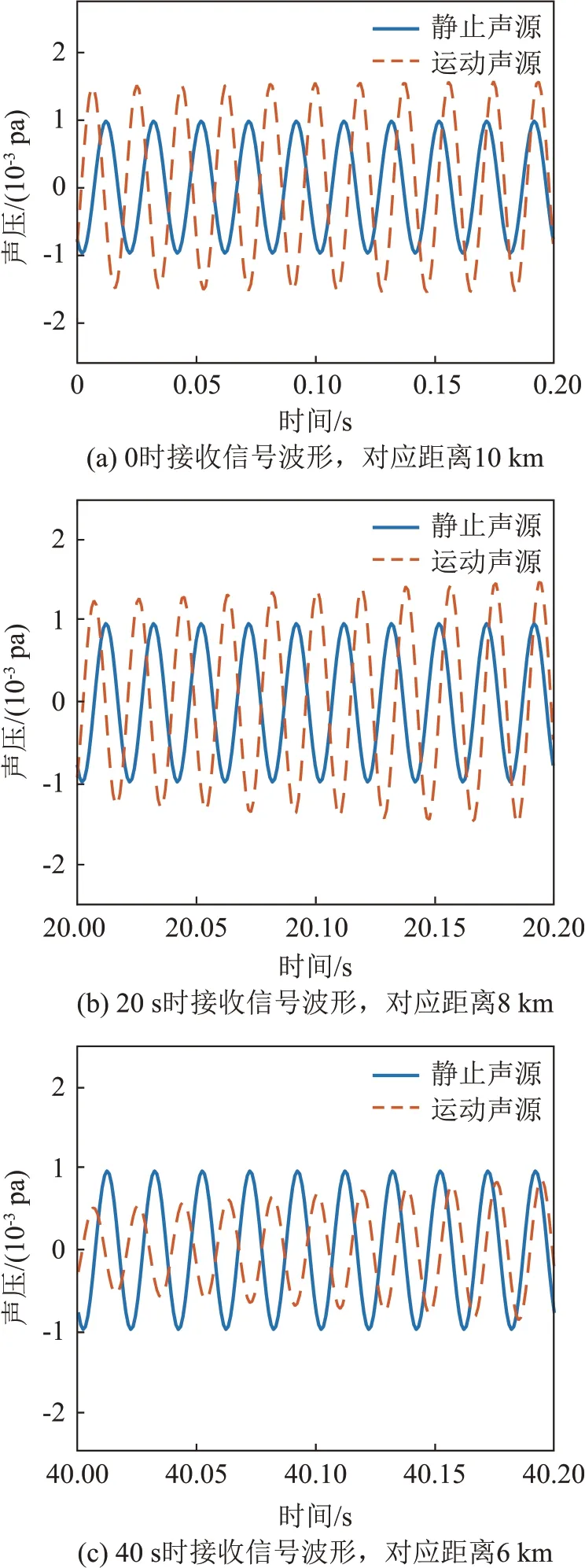
图8 不同时刻浅海Pekeris波导接收信号的时域波形Fig.8 Received signal waveforms in the shallow-sea Pekeris waveguide environment at different times

在浅海Pekeris 波导中，声源产生的声波会沿不同的路径到达接收器，除了直达声波外，还存在经过海面和海底多次反射后的声波。由于声源的运动，不同传播路径的声波会产生不同的多普勒频移，2.1 节的多普勒频移求解公式仅适用于对直达声波的求解。

图9 为计算得到声源通过接收器正上方的50～150 s 时间区间接收信号的瞬时频率与直达声波的多普勒频移理论值的比较，可以看到当声源靠近接收器时接收信号频率大于原始频率，远离时小于原始频率。由于直达声波具有最大的多普勒频移，沿其他路径传播的声波多普勒频移小于直达声波，因此当声源接近接收器时仿真得到接收信号的瞬时频率略小于直达声波的多普勒频移。由于在Pekeris波导中运动声源与接收器的水平距离随时间发生变化，接收信号的幅度会随时间发生起伏。在幅度较小处的瞬时频率会发生较大的变化，因此在图8中可以看到计算得到的瞬时频率存在突变。

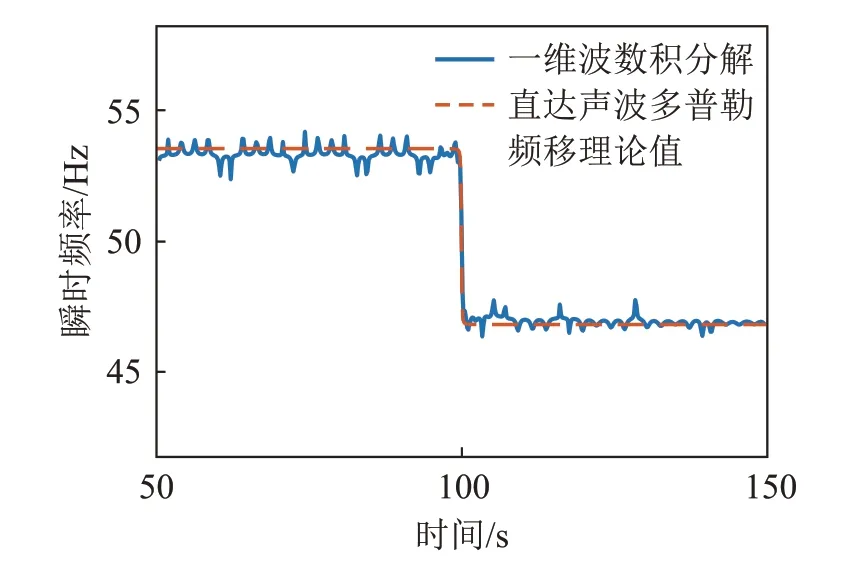
图9 一维波数积分解得到的信号瞬时频率与理论值对比Fig.9 Comparison between the signal instantaneous frequency obtained by the one-dimensional wavenumber integration solution and the theoretical value

截取并放大70～80 s 时刻的时域波形和瞬时频率，如图10所示。由图10中的仿真结果可以看到瞬时频率突变的时刻与波形幅度极小值相吻合。

对0～80 s的接收信号进行傅里叶变换得到接收信号的频谱，如图11所示。可以看到接收信号的频谱有多个谱峰，这是由于Pekeris 波导中存在多途效应，声波沿多条路径到达接收器。通过KRAKENC模拟得到该波导环境下50 Hz的声源会产生4 阶简正波，不同的简正波有不同的相速度，因此也就有不同的多普勒频移[9]，当声源的运动轨迹通过接收器的正上方，各阶简正波的频移不会发生改变，因此接收的信号为多个单频信号，在图11中显示了多个谱峰，谱峰的位置是由波导条件决定的。

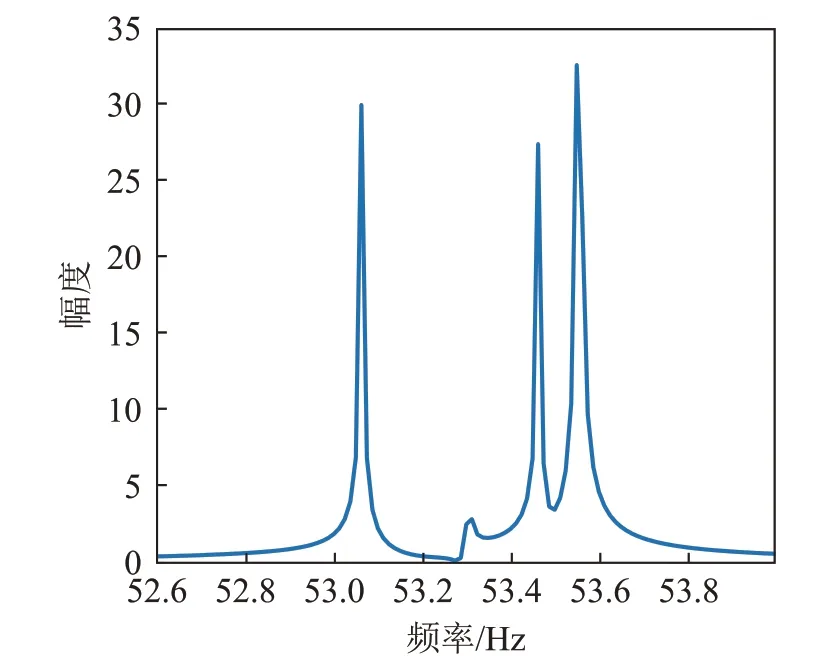
图11 在0～80 s时间内接收信号频谱Fig.11 The spectrum of the received signal from 0 to 80 s

改变接收器的深度，并计算接收信号的频谱，得到的结果如图12所示，图中橙色虚线和紫色点划线分别为接收器在66 m、86 m 深度时接收信号的频谱。可以看到谱峰的高低发生了变化，但是对应的频率并没有改变。将声源频率改为35 Hz，接收信号的频谱如图13所示。利用Krakenc计算该波导环境的简正波函数，可以得到3阶简正波，与图13中的3个谱峰相对应。

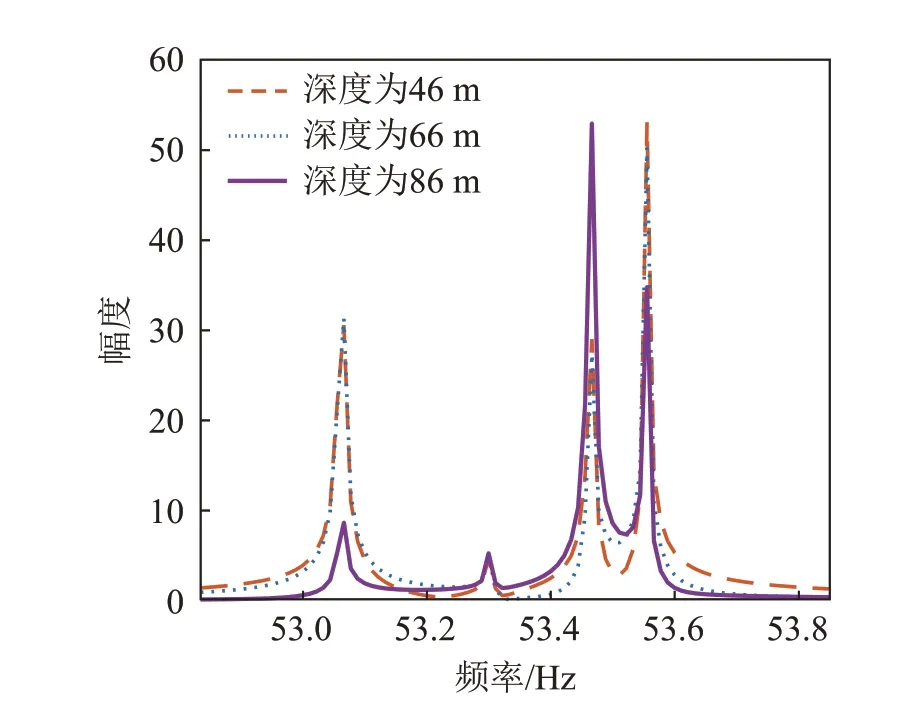
图12 不同深度接收信号的频谱Fig.12 Spectrums of the received signals at different depths

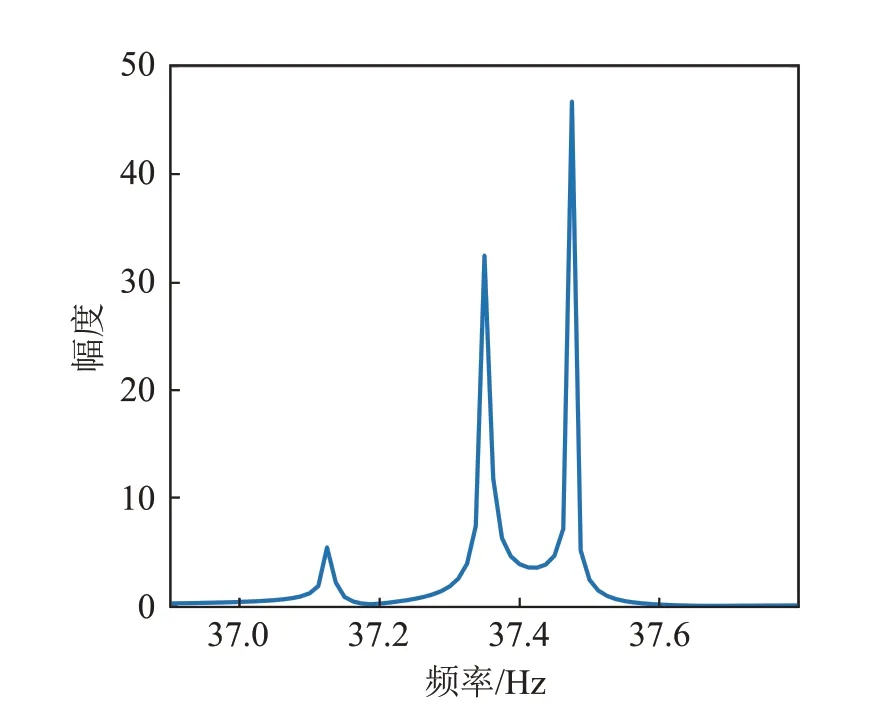
图13 声源频率为35 Hz时接收信号的频谱Fig.13 The spectrum of the received signal at the sound source frequency of 35 Hz

目前水下航行器和水下武器的运行速度还难以达到100 m∙s-1，因此在相同波导环境下对相对低速运动的声源进行仿真。声源声速为50 m∙s-1和20 m∙s-1时仿真得到0～80 s 接收器接收信号的时域波形如图14所示。与图7 相比，声源运动速度减小，接收信号幅度的变化速度也变缓。

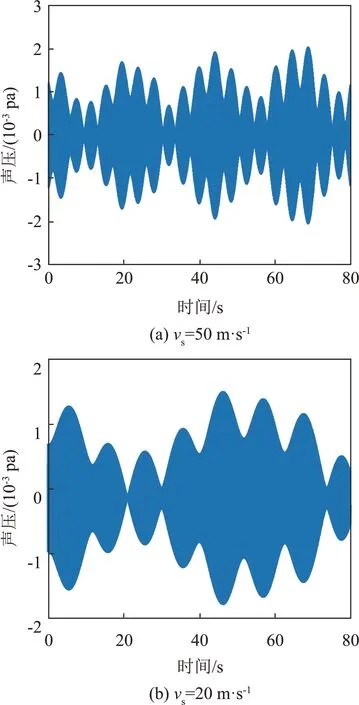
图14 声源不同速度运动时接收器的时域波形Fig.14 The time domain waveforms of the received signals when the sound source moves at different speeds

图15 为不同运动速度时接收信号的时频图，可以看到当声源运动速度减小时，接收信号的多普勒频移也会减小。从图15 中的颜色深浅变化也能看出速度越快接收信号变化得越快。

图15 声源不同速度运动时接收信号的时频图Fig.15 Time-frequency diagrams of the received signals when the sound source moves at different speeds

3 结论

本文为求解Pekeris 波导中运动声源的声场提供一种新思路，将Pekeris 波导中静止声源的数值稳定波数积分解应用到运动声源的声场分析中。在仿真实验中，验证了二维波数积分的一维近似数值解的正确性，并仿真分析了Pekeris 波导下运动的单频点源产生的声场。波数积分方法是直接数值求积分的方法，本文只在远场条件下引入较小的误差。利用数值稳定的计算方法来求解运动声源的深度格林函数，不存在数值溢出的问题。因此本文的方法可以作为研究Pekeris 波导中运动单频点源的远场特性的参考模型来应用。