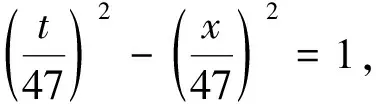关于椭圆曲线y2=(x+47)(x2+472)的整数点
2024-01-16华程
华 程
(泰州学院 数理学院,江苏 泰州 225300)
1 主要结论
许多学者关注椭圆曲线
y2=(x+P)(x2+P2)
(1)
的整数点问题,这里P为奇素数.其中文献中,Weger利用较高深的方法对P=167,223,337,1201找到了(1)的全部整数点,分别是
当P=167时,(1)仅有整数点(x,y)=(-167,0);
当P=223时,(1)仅有整数点(x,y)=(-223,0);
当P=337时,(1)仅有整数点(x,y)=(-337,0),(-287,±3130),(2113,±105910)和(56784,±13571615);
当P=1201时,(1)仅有整数点(x,y)=(-1201,0),(599,±56940),(1999,±131920)和(58849,±14424010)。
本文利用初等方法研究了P=47的整数点,获得如下定理
定理椭圆曲线
y2=(x+47)(x2+472)
(2)
仅有整数点(x,y)=(-47,0)。
2 一些引理
引理1 设P为素数,a为任一整数,则p|a或(P,a)=1。
证明:参见文献(p27,定理1.17)。
引理2 不定方程x2+y2=z2适合条件(x,y)=1,2|x的全部正整数解可表示为
x=2ab,y=a2-b2,z=a2+b2,其中a>b>0,(a,b)=1,2+(a+b)
证明:参见文献(p110,定理3.4)。
引理3 设p为素数,e≥0,则不定方程
(2epy2-1)2-2z2=-1
仅有正整数解z=1,5和p=2.
证明:参见文献(p69,习题2)。
引理4 不定方程x2+y2=z2适合条件(x,y)=1,x>y的全部正整数解可表示为
x=m2-n2+2mn,y=|m2-n2-2mn|,z=m2+n2
其中m>n>0,(m,n)=1,2⫮(m+n)。
证明:参见文献(p117,习题5)。
引理5 设p是一个素数,若不定方程u2-Dv2=±p有整数解,则当p|2D时,有1个结合类;当p⫮2D时,有2个结合类.
证明:参见文献(p33,定理4)。

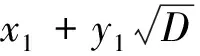
证明:参见文献(p32,定理3)。
引理7 不定方程
x2-2y4=47
(3)
仅有正整数解(x,y)=(7,1)。
证明:由引理5、引理6知,方程X2-2Y2=47的一般解可由以下2个非结合类给出

这里n∈,是方程X2-2Y2=47的基本解,为Pell方程U2-2V2=1的基本解。
若方程(3)有整数解,必有n,使得
y2=±(un+7vn)或y2=±(un-7vn)=±(u-n+7v-n)
当n≥0时,un+7vn>0;当n<0时,un+7vn<0.因此可以归结为
y2=un+7vn,n≥0
(4)
或
y2=-un+7vn,n>0
(5)
易知,有
un+2=6un+1-un,u0=1,u1=3
(6)
vn+1=6vn+1-vn,v0=1,v1=2
(7)
u2n=un2+2vn2=2un2-1=4vn2+1,v2n=2unvn
(8)
un+2km=(-1)kun(modum),vn+2km≡(-1)kvn(modum)
(9)
先讨论(5)式(约定:用“T”表示取模所得剩余序列的周期)。
对(5)式取模8,得T=4,且当n≡0,1,2,3(mod4)时,-un+7vn≡7,3,3,7(mod8)均为模8的平方非剩余,故(5)式不成立。
再讨论(4)式。
对(4)式取模8,得T=4,且当n≡2,3(mod4)时,un+7vn≡5(mod8)为模8的平方非剩余,故排除,剩n≡0,1(mod4)。
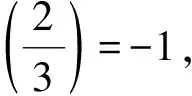
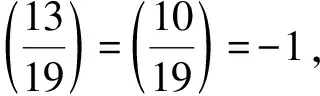
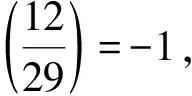
当n≠0时,可令n=2×2t×5×(2k+1),t≥1,且令
则2m≡2(mod3)。
由(9)式可得
y2≡±(u2m+7v2m)≡±7v2m(modu2m)
(10)
注意到2|m时,um≡1(mod8),u2m≡1(mod8)。令2s‖vm结合(8)式,则(10)式成为
(11)
因为{un}模7的剩余序列的周期为3,1,3,3,1,3,3,…,且当2m=2(mod3)时,u2m≡3(mod7),u2m≡3(mod7)所以(11)式变为
矛盾。因此n=0,此时y2=u0+7v0=1,故y=1,从而x=7,于是(3)仅有正整数解(x,y)=(7,1)
证毕。
3 定理的证明
设(x,y)是(2)式的任意整数点.因为x2+472>0,所以由(2)式知,x≥-47。
当x=-47时,可得(2)式的整数点为(x,y)=(-47,0),
当x=0时,(1)式可化为y2>473,显然没有整数解。
因此,下面只需考虑-47
情形Ⅰ -47 表1 椭圆曲线-47 综上,此情形,椭圆曲线(2)无整数点。 情形Ⅱx>0 令(x+47,x2+472)=d,则d=(x+47,2×472),所以d|2×472,即d∈{1,2,47,2×47,472,2×472}。 ①当d=1时,(2)式可化为 x+47=s2,x2+472=t2,y=±st (12) 其中s>0,t>0,(s,t)=1。 x=2uv,47=u2-v2,t=u2+v2 (13) 其中u>v>0,(u,v)=1,u,v为一奇一偶。 由(13)的第2式得(u+v)(u-v)=47,所以u+v=47,且u-v=1。解得 u=24,v=23,代入(13)的第1式得x=1104。 此时,y2=52×132×172×1151,显然无整数解。 ②当d=2时,(2)式可化为 x+47=2s2,x2+472=2t2,y=±2st (14) 其中s>0,t>0,(s,t)=1。 如果47|x,则由(14)知47|s且47|t。令x=47x1,s=47s1,t=47t1,代入(14)得 x1+1=2×47s12,x12+1=2t12 其中x1>0,s1>0,t1>0,消去x1, 得 (2×47s12-1)2-2t12=-1 (15) 根据引理3,方程(15)无正整数解。 如果47⫮x,即(47,x)=1,则由(14)的第2式知,x,t都是奇数。根据引理4,可得 47=m2-n2+2mn,x=|m2-n2-2mn|,t=m2+n2 (16) 或 x=m2-n2+2mn,47=|m2-n2-2mn|,t=m2+n2 (17) 其中m>n>0,(m,n)=1,2⫮(m+n)。 先讨论(16)式。 由(14)式的第1式及(16)知,当x=m2-n2-2mn时,有 s2=m2-n2 (18) 考虑到2⫮s,由(18)式及引理2可得 s2=f2-g2,n=2fg,m=f2+g2 (19) 其中f>g>0,(f,g)=1,2⫮(f+g)。 将(19)式的后两式代入(16)式的第一式整理得 47=f4+4f3g-2f2g2+4fg3+g4,2⫮(f+g) 对上式两边取模8,得-1≡1(mod 8),显然不可能。 当x=-m2+n2+2mn时,有s=2mn.因(m,n)=1,故得 m=f2,n=2g2 (20) 或 m=2g2,n=f2 (21) 将(20)代入(16)式的第一式整理得 47=f4-4g4+4f2g2 上式两边取模8,得-1≡1(mod8),显然不可能。 将(21)代入(16)式的第2式整理得 47=-f4+4g4+4f2g2 即 (2g2+f2)2-2f4=47 (22) 根据引理7,由(22)式得出2g2+f2=7且f=1。 于是g2=3,无整数解。 再讨论(17)式。 由(14)式的第一式及(17)知,当47=m2-n2-2mn时,有s2=m2-n2.类似(18)的讨论可得 47=f4-4f3g-2f2g-2f2g2-4fg3+g4,2⫮(f+g) 对上式两边取模8,得-1≡1(mod8),不可能。 当47=-m2+n2+2mn时,有s2=2mn,类似(20)与(21)式的讨论可得 47=-f4+4g4+4f2g2 即(22)式无整数解。 ③当d=47时,(2)式可化为 x+47=47s2,x2+472=47t2,y=±47st (23) 其中s>0,t>0,(s,t)=1。 由(23)式可知 47|x且47|t.设x=47x1,t=47t1,代入(23)得 x1+1=s2,x12+1=47t12 (24) 其中x1>0,t1>0。 若2|t1,对(24)的第二式取模4,知不可能,故2⫮t1由(24)的第一式代入第二式可得 47t12=s2-2s2+2,2⫮s 对上式两边取模8得-1≡(mod8),也不可能。 ④当d=2×47时,(2)式可化为 x+47=2×47s2,x2+472=2×47t2,y=±2×47st (25) 其中s>0,t>0,(s,t)=1。 若2|t1则(26)的第二式得出x12≡7(mod8),不可能,因此2⫮t1,由(26)的第一式代入第二式得 47t12=2a4-2a2+1 对上式取模8得-1≡1(mod8),也不可能。 ⑤当d=472时,(2)式可化为 x+47=472s2,x2+472=472t2,y=±472st (27) 其中s>0,t>0,(s,t)=1。 由(27)可知 47|x,设x=47x1(x1>0),代入(27)的第二式得x12+1=t2,推出x1=0。从而x=0,与x>0矛盾。 6)当d=2×472时,(2)式可化为 x+47=2×472s2,x2+472=2×472t2,y=±2×472st (28) 其中s>0,t>0,(s,t)=1。 由(28)可知,47|x。设x=47x1(x1>0)代入(28)得 x+1=2×47s2,x12+1=2t2 于是有(2×47s2-1)2-2t2=-1.根据引理3,此方程无正整数解。 综上,椭圆曲线(2)仅有整数点(x,y)=(-47,0)。 证毕。