基于NSM 分析双线隧道下穿对既有隧道影响
2024-01-16江思岑柴天建颜建伟
江思岑,柴天建,颜建伟
(华东交通大学土木建筑学院,江西 南昌330013)
随着城市轨道交通的快速发展,地下空间中隧道间的交叉不可避免[1-2],双线隧道下穿既有隧道施工工程日益增多, 为确保既有隧道的运营安全,进行对隧道下穿施工引起既有隧道沉降预测问题的研究十分重要[3-5]。
目前,国内外学者对新建隧道穿越既有隧道工程方面展开大量研究,取得了丰硕的成果,一般采用数值模拟[6-9]、模型试验[10]以及理论解析[11-13]等方法。 胡秋斌[14]通过三维有限元数值模拟,分析了新建盾构隧道既有暗挖隧道的受力变形状态。 张治国等[15]基于位移控制Schwarz 交替法和复变函数理论,提出了双线盾构隧道在任意布置方式下开挖引起周围地层变形的计算方法。 于霖等[16]将既有隧道简化成Pasternak 地基模型上的Euler-Bernoulli 梁,基于两阶段法分析既有隧道力学响应。 蔡光伟等[17]基于当层法原理,考虑既有隧道与新建隧道轴线间夹角对沉降的影响,结合既有结构的刚度分析,推导出隧道斜交下穿既有隧道在任意地层沉降变形曲线计算公式。 Li 等[18]考虑剪切效应,将Timoshenko梁模型运用到隧道变形分析中,发现大直径盾构隧道的剪切效应更为明显且适用。 冯国辉等[19]在新建隧道下穿既有隧道引起的隧-土相互作用时, 采用修正的高斯公式解得土体自由位移,将既有隧道简化成Kerr 地基模型上的Euler-Bernoulli 梁,求得既有隧道受力变形解析解, 分析了新旧隧道夹角、地层损失率及新建隧道埋深变化对既有隧道变形响应的影响。 结果表明:新建隧道地层损失率增大,既有隧道沉降增大;新旧隧道轴线夹角、高差的增大,既有隧道沉降减小。
本文基于零空间法(Nullspace Method),对计算步骤进行简化,与深圳地铁9 号线下穿地铁4 号线实测数据进行对比,进一步研究新建双线隧道间距与土体损失对既有隧道沉降变形影响,可为实际工程设计与施工提供理论参考。
1 基本计算方程建立
1.1 既有隧道纵向沉降
既有隧道假定为Pasternak 双参数地基上具有等效纵向抗弯刚度EeIe的Euler-Bernoulli 梁, 其微分控制方程为
式中:w(x)为既有隧道的位移函数;G 为弹性地基剪切层参数;EeIe为既有隧道等效纵向抗弯刚度;q(x)为土体自由场竖向位移产生的荷载;DO为既有隧道外径;k 为地基弹性系数。
控制方程式(1)两边乘以位移并对全长积分得
式中:l 为既有隧道全长。
隧道件自由放置在土体中,端部弯矩和剪力为0,边界条件数学描述如下据此,式(2)转化为
式中:KL为土体刚度矩阵;M 为边界条件约束矩阵;P 为新建双线隧道施工引发的土体位移荷载;f 是f 的矢量形式。 从式(11)上式可以发现初始假设的场函数与边界约束无关,解决了边界条件对场函数选择的限制问题;式(11)下式是边界条件对场函数权重系数选择的限制,即权重系数存在线性相关,称为零空间法。 通过MATLAB 零空间法Z=null (M) 解出约束矩阵M 的零空间解集,有

1.2 土体自由场竖向位移
1998 年,Loganathan[20]提出自由土体竖向位移半解析式,本文用于计算隧道开挖对周围土体及既有构筑物作用。 依据该方法,第一、二条隧道开挖引起的土体自由场竖向位移U1(x)和U2(x)分别为
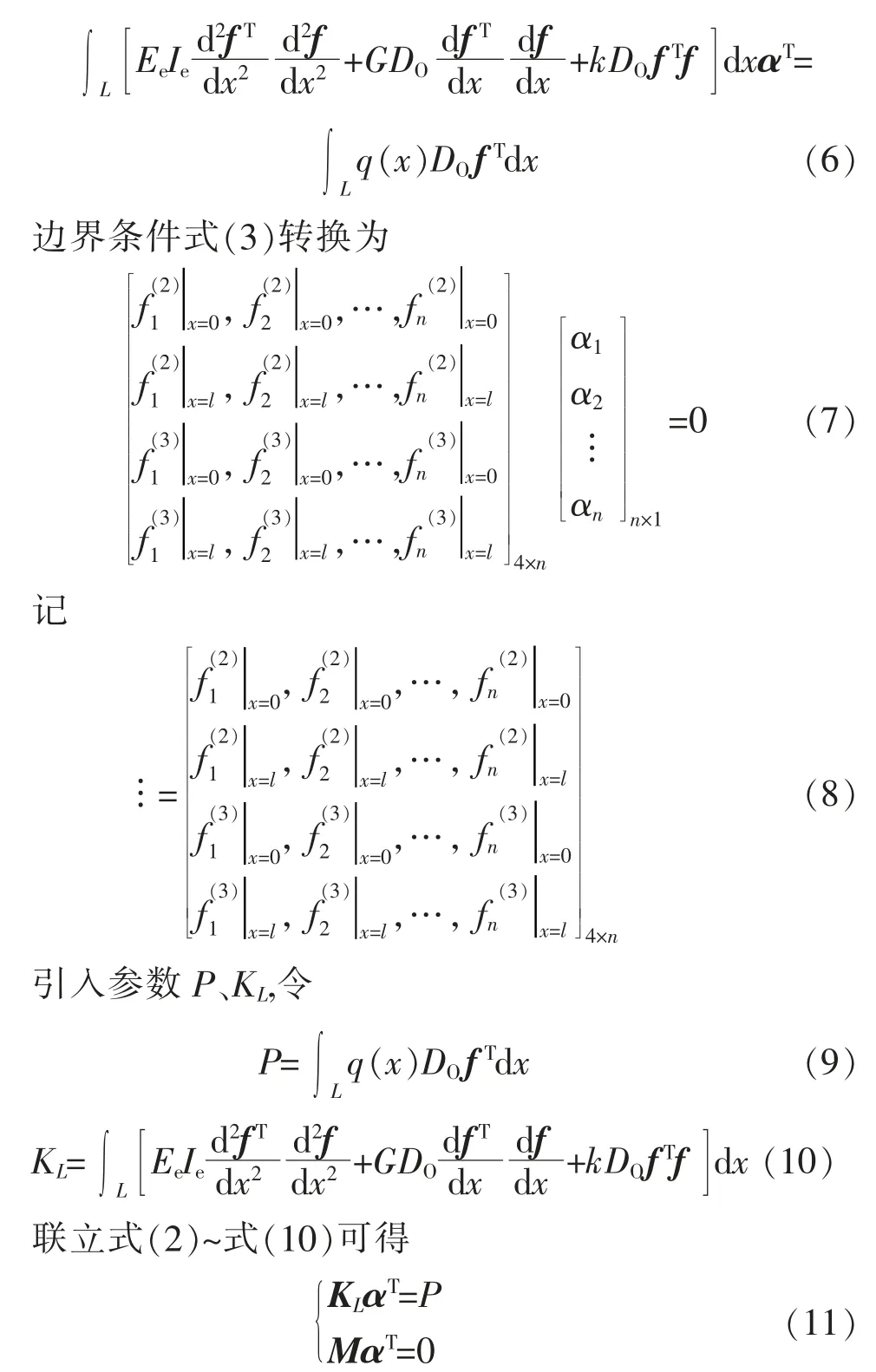
式中:R 为新建隧道的开挖半径;L 为双线隧道轴线之间的水平距离;ε1,ε2分别为第一条隧道和第二条隧道开挖时引起的土体损失。 计算模型图如图1 所示,图中z 为既有隧道轴线埋深;H1,H2分别为第一、第二条隧道轴线埋深;υ 为土体泊松比;a 为新建隧道轴线与既有隧道轴线之间的夹角。依据叠加原理可知双线隧道开挖引起的土体自由场竖向位移U(x)为
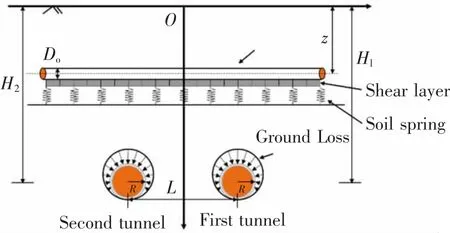
图1 计算模型示意图Fig.1 Diagram of the calculating model
1.3 土体损失
新建双线盾构隧道施工过程中,第二条隧道开挖引发的土体损失大于第一条开挖的隧道,其原因是第一条隧道的开挖会对周围土体造成扰动。 双线隧道间距越小,土体损失差值越大;反之间距越大,差值越小。 据Jin 等[21]整理的实验数据可知,双线隧道土体损失满足以下关系
式中:c 为开挖扰动系数;D 为新建隧道外径。
1.4 剪切层参数及地基基床系数
基于Tanahashi 等[22]给定的Pasternak 地基模型剪切层参数G 如下
式中:Es为土体弹性模量;t 为土体剪切层厚度,依据徐凌[23]研究,t 的取值为
根据Vesic[24]提出的经验公式及Attewell 等[25]的修正,俞剑等[26]考虑到地基弹性系数受埋深深度的影响,在此基础上引入深度参数η,完善后的地基弹性系数k 的计算公式为
2 算例验证
选取深圳地铁9 号线下穿既有地铁4 号线工程[27]为例对本文零空间法进行验证。 该工程剖面图与平面图分别如图2,图3 所示,其中为既有隧道内径。 新旧隧道夹角为83°,轴线埋深分别为20.5 m 和12.0 m,其余参数参考甘晓露等[28]取值,如表1 所示。

表1 隧道计算参数Tab.1 Tunnel calculation parameters
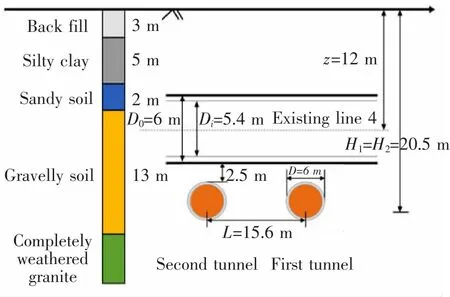
图2 既有隧道及新建隧道剖面图Fig.2 The cross-sectional view of the existing and new tunnels
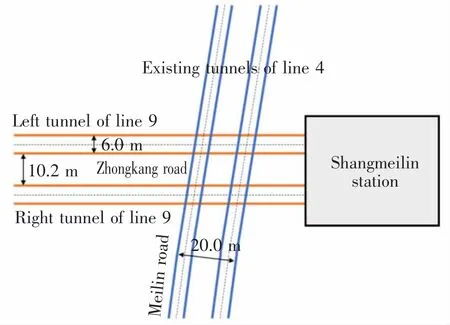
图3 既有隧道及新建隧道平面图Fig.3 The plan view of the existing and new tunnels
零空间法计算结果与工程实测数据的对比情况如图4 所示。 由图4 可知,零空间法呈现规律与实测基本一致,线性吻合,两条隧道发生沉降的范围均与实际测得范围相符。 实测第一条隧道的最大沉降变形为5.34 mm,预测最大沉降变形为5.67 mm;第二条隧道的最大沉降变形为6.93 mm, 预测最大沉降变形为6.72 mm,预测结果与实测值吻合,且最大沉降处坐标位置相同。 由于第一条隧道开挖后存在土体扰动现象,造成第二条隧道的土体损失率增大,因此第二条隧道开挖引发的纵向位移明显大于第一条隧道开挖,预测结果与工程实测数据依然吻合的很好,再次证实了本方法的准确性。
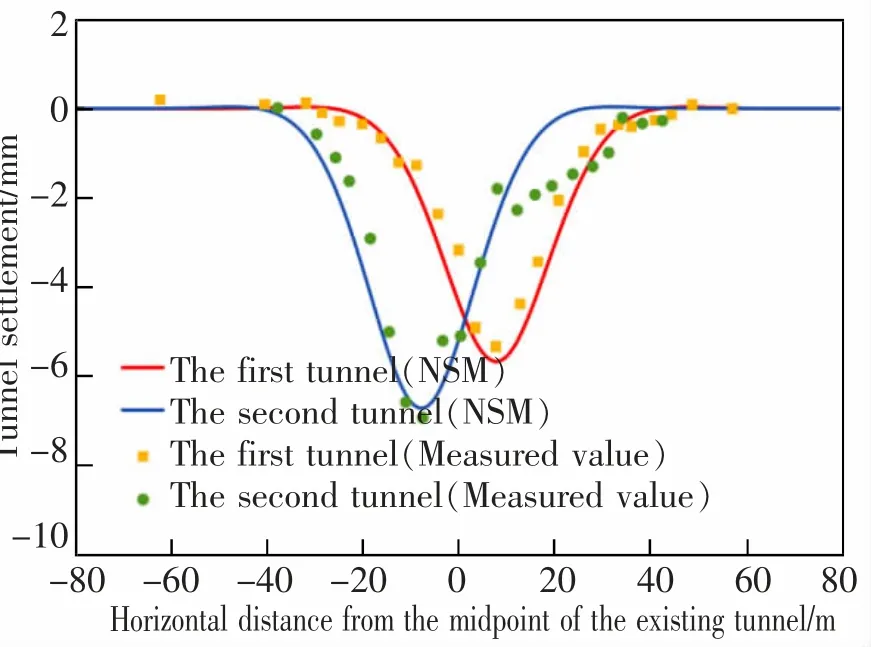
图4 沉降计算结果对比图Fig.4 Comparison of settlement calculation results
3 参数分析
考虑不同物理参数变化对既有隧道纵向位移的影响,采用前文建立的模型基础及参数,分别改变新建隧道间距L,土体损失ε1,新旧隧道轴线夹角a以及新建隧道埋深H1,进行计算分析,研究隧道沉降规律。
3.1 新建隧道间距L 变化对既有隧道沉降影响
为探究新建隧道两线间距离L 对既有隧道纵向位移的影响, 研究新建隧道外径D 的10 倍范围内的影响规律,计算结果如图5 所示。
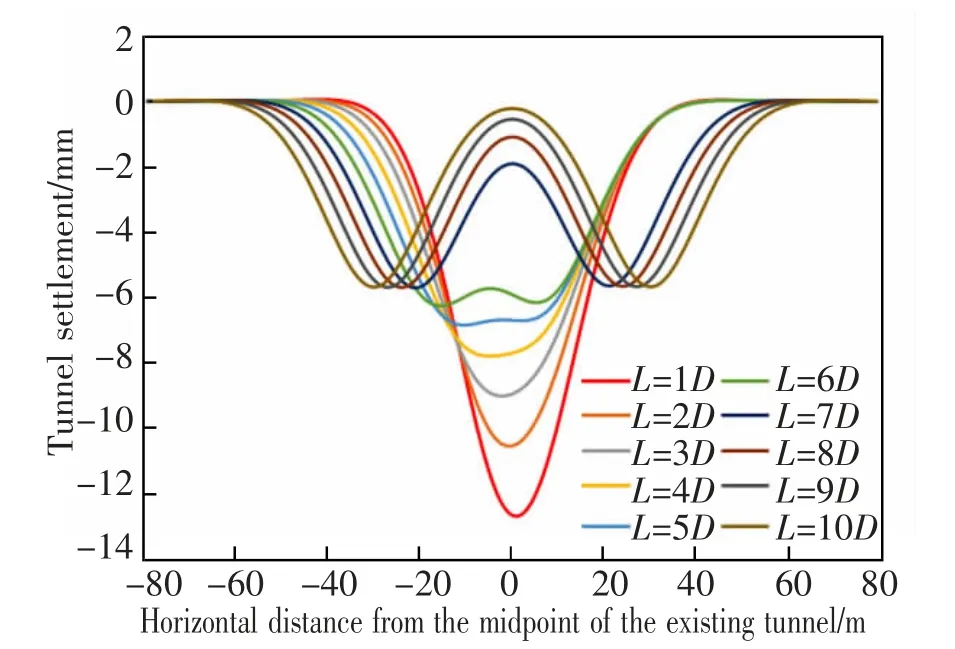
图5 不同隧道间距对应既有隧道竖向位移Fig.5 Vertical displacement with different tunnel distance
从图5 可以看出, 增大新建隧道两线间距,既有隧道沉降形态由“V”形变化为“U”形进而转变为“W”形。 随着间距的增大,沉降范围扩大,既有隧道纵向沉降不断减小。 继续增大间距,双线隧道间影响越来越弱, 沉降形态趋于稳定, 呈近乎标准的“W”形,第一条隧道开挖与第二条隧道开挖所引发既有隧道的纵向位移几乎相等,即两条隧道的开挖无相互影响。 如图6 所示,从右至左分别为新建隧道间距L 为D~10D 的既有隧道最大竖向位移,可知近距离的双线开挖会引发较大的沉降,易对实际工程产生很大风险。 在施工合理范围内,适当增大双线间距离能有效减少沉降,间距在7 倍新建隧道外径范围中,沉降由12.69 mm 减至5.70 mm,该减少沉降方法效果显著。 大于7 倍外径后,双线隧道间干扰甚微,沉降量稳定在5.70 mm 左右。
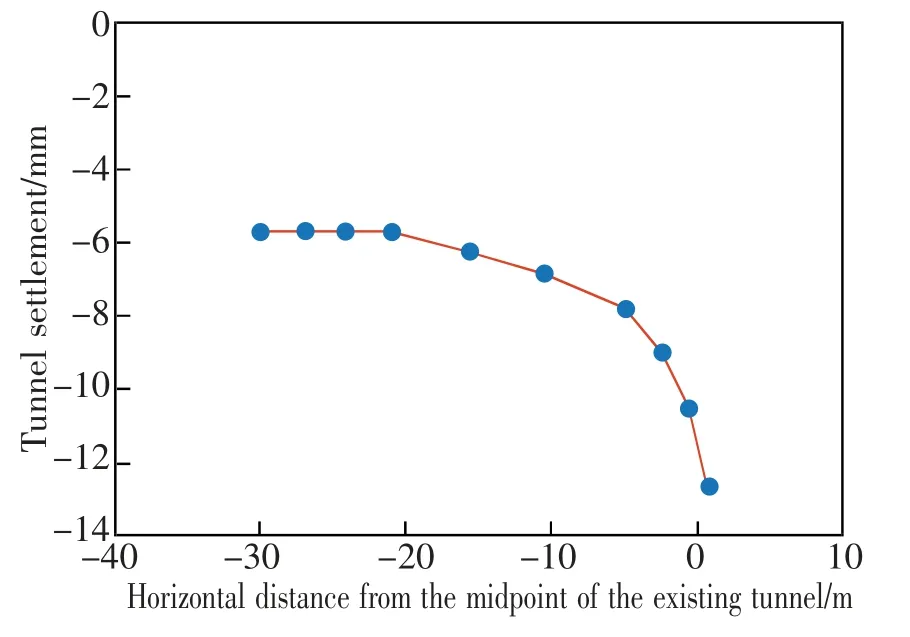
图6 不同间距下新建隧道最大沉降Fig.6 Maximum settlement with different tunnel distance
3.2 土体损失ε1 变化对既有隧道沉降影响
控制其它参数不变,取5 组土体损失ε1研究其对既有隧道纵向位移的影响, 分别为0.25%,0.50%,1.00%,1.50%和2.00%, 计算结果如图7 和图8 所示。由图7 可知,随着土体损失ε1增大,既有隧道沉降范围无明显变化, 纵向位移最大值增大,由4.79 mm 变化为38.30 mm。 由图8 可知,在离既有隧道模型中点特定位置处的纵向位移也是随土体损失ε1增大而增大。 此外,随着土体损失率的增加,所受附加应力呈线性增加,因此距离中点处0,20 m 处的纵向变形亦呈现近似线性变化。 显然,在实际工程中减小土体损失是控制隧道沉降的重要举措之一。
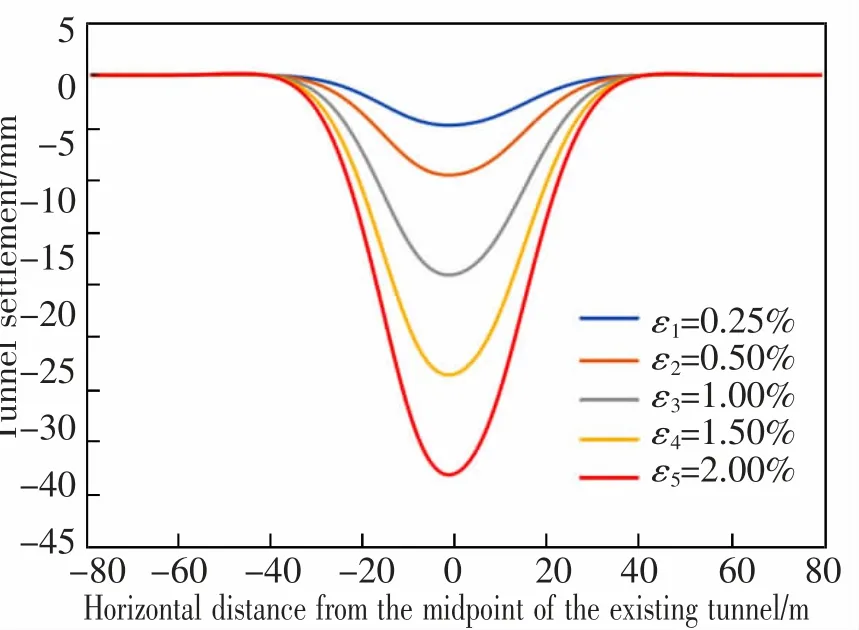
图7 不同土体损失对应既有隧道竖向位移Fig.7 Vertical displacement with different ground losses
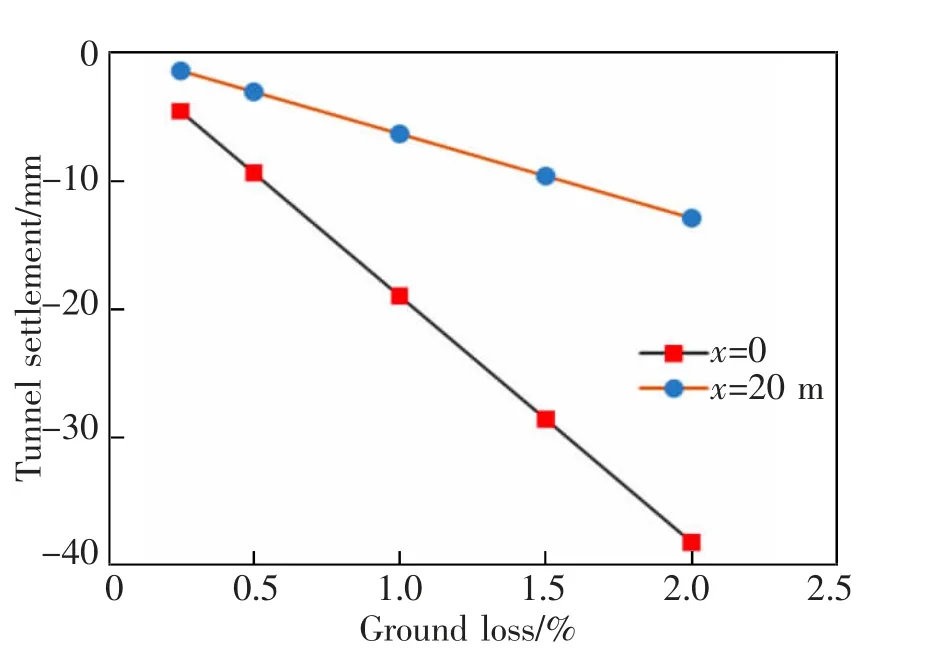
图8 不同土体损失下既有隧道特定位置处位移Fig.8 Specific position displacement of tunnel under different ground losses
3.3 新旧隧道夹角a 变化对既有隧道沉降影响
取6 组不同新旧隧道夹角a 分析其对既有隧道沉降变形的影响, 分别为15°,30°,45°,60°,75°,90°,计算结果如图9 与图10 所示。 由图9 可知,随着新旧隧道轴线夹角的增大,既有隧道沉降范围变窄, 且纵向位移减小。 当新旧隧道轴线夹角为15°时, 既有隧道模型在-80~80 m 范围内均存在明显沉降,发生沉降的范围很广且沉降量大,最大沉降值达14.46 mm; 当新旧隧道轴线夹角为90°时,主要沉降范围集中在-40~40 m 之间, 最大沉降减小为9.53 mm。其原因为新旧隧道间相交范围变小(如图11),相交形态由近乎“重合”向正交形态转变,作用范围减小。 由图10 可知,既有隧道最大竖向位移在15°~45°近乎线性变化, 继续增大新旧隧道轴线夹角,既有隧道沉降变化速率减缓。 因此,在工程设计中,在实际工况允许的情况下尽量将新建隧道与既有隧道设计为正交形式,能够大幅度缩小既有隧道发生沉降的区间且减小最大纵向位移,降低工程施工风险。
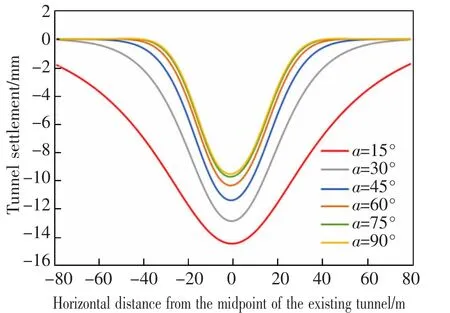
图9 不同夹角对应既有隧道竖向位移Fig.9 Vertical displacement with different skew angles
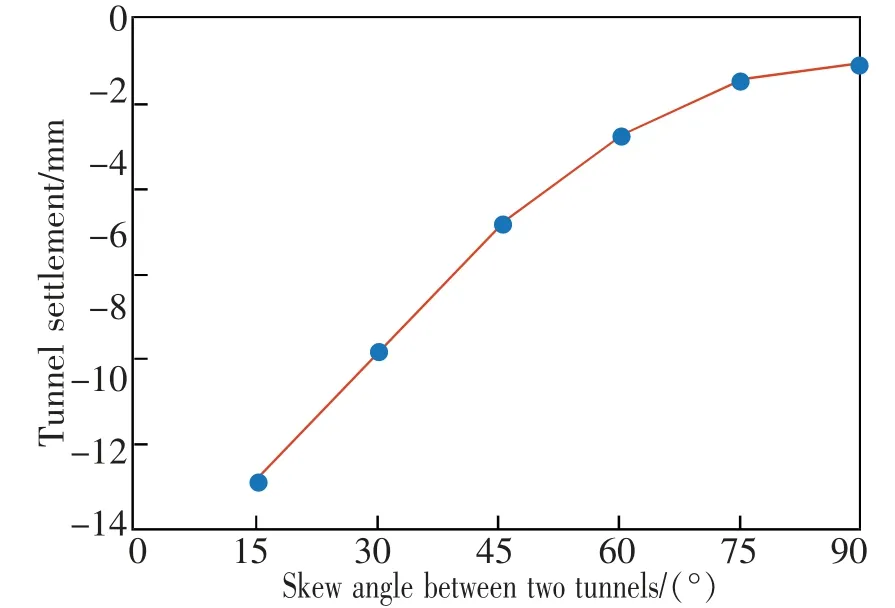
图10 不同夹角对应既有隧道最大竖向位移Fig.10 Maximum settlement with different skew angles between two tunnels
3.4 新建隧道埋深H1 变化对既有隧道沉降影响
为探究新建隧道在不同埋深深度下对既有隧道沉降变形的影响,本文取6 组埋深进行计算分析,取值分别为:20,22,24,26,28,30 m,计算结果如图12 和图13 所示。如图所示,当埋深为20 m 时,沉降曲线窄而深,沉降主要发生在-40~40 m 范围内,最大沉降为9.63 mm;当埋深为30 m 时,沉降范围扩大,主要沉降区间为-60~60 m,最大沉降为8.09 mm。因此在实际工程设计与施工中,应当综合考虑沉降范围与最大沉降的影响,权衡出最为安全且经济的施工方案。

图12 不同新建隧道埋深对应既有隧道竖向位移Fig.12 Vertical displacement with different depth of the new tunnel
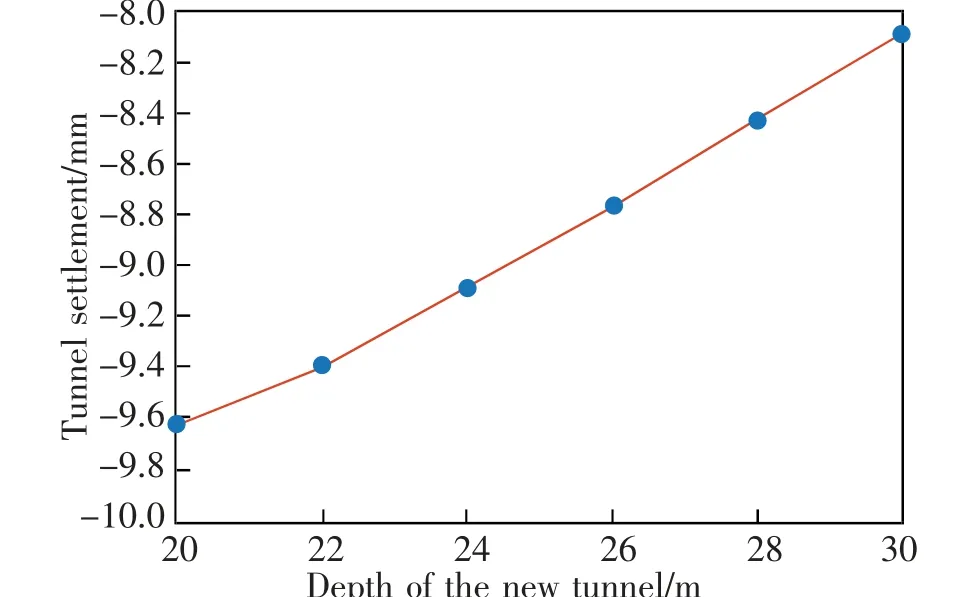
图13 不同埋深对应既有隧道最大竖向位移Fig.13 Maximum settlement with different depth of the new tunnel
4 结论
1) 双线隧道水平间距增加在其外径1~7 倍范围内可以有效控制既有隧道沉降,沉降形态由最初的“V”形变化为“U”形进而转变为“W”形。超过7 倍后,沉降形态趋于稳定且标准的“W”形,沉降量也保持稳定。
2) 既有隧道沉降变形会随着土体损失增大,沉降范围无明显变化,最大纵向位移呈线性变化。
3) 随着新旧隧道轴线夹角增大,既有隧道发生沉降的范围变窄,最大纵向位移减小。
4) 随着新建隧道埋深的增大,既有隧道最大纵向位移减小,沉降范围变广。
