基于模型预测控制的风储联合电场参与电网二次调频策略

刘传斌, 矫文书, 吴秋伟, 陈 健, 周 前

(1.山东大学 电气工程学院,济南 250061; 2.清华大学 清华伯克利深圳学院;清华深圳国际研究生院,广东 深圳 518055; 3.国网江苏省电力有限公司电力科学研究院,南京 211100)

随着电力电子技术的发展,风力发电(简称风电)技术取得了迅速进步,风力发电机结构已从最开始的定桨距结构发展为变桨距结构.变桨距结构捕获风能效率较高,在高风速下风能利用率更高,变桨距调节逐渐成为兆瓦级以上风力发电机参与二次调频的研究重点.储能系统由于快速响应、精准跟踪的特性,配合风电机组参与电网调频,能够有效提高电网二次调频的效果.

双馈异步风力发电机(Doubly Fed Induction Generator,DFIG)通常运行在最大功率点跟踪(Maximum Power Point Tracking,MPPT)控制状态,风力发电机转子转速与电网频率完全解耦,不具备类似于同步发电机的惯性响应和长时间调频能力.因而,高渗透率风电接入电力系统时会引起电网调频能力不足等问题[1].针对这些问题,国内外的电网并网导则中均明确指出并网风力发电机须提供调频服务[2].因此在电网进行二次调频时,风力发电机需运行在减载模式,以便及时响应系统频率变化,维持频率稳定.目前,风力发电机参与调频的基础控制方式包括虚拟惯性控制、转子转速控制和桨距角控制3种[3].高渗透率风电的电力系统面临严峻的调频负担,而且风场可以提供的调频容量有限,因此亟需新的调控手段.例如,风电场辅以储能系统,借助储能系统的快速响应能力,可以减少风场的减载备用功率,快速响应电网二次调频的要求[4].

近年来,研究者对风力发电机参与电网频率调节进行大量研究并取得了可观成果.文献[5]中利用风力发电机中电力电子器件对功率的快速控制能力为频率的偏移提供了短时有功支撑.文献[6-7]中利用变流器快速的功率调节能力,通过释放风力发电机转子的动能,增强系统惯性.但是最大功率跟踪会影响虚拟惯性控制,转子动能提供频率支撑能力有限,因此转子控制策略只能提供短时的有功功率支撑并容易产生频率的二次跌落问题.为了提升风力发电机持续提供有功功率的能力并解决频率二次跌落问题,研究者提出了桨距角控制方案和风储联合调频控制方案.文献[8]中提出了一种根据上级系统命令控制桨距角的调频控制策略,使风力发电机具备在复杂工况下连续运行的能力;文献[9]中提出将储能系统加入风电场中进行频率控制,解决频率的二次跌落问题.文献[10]中在考虑储能单元荷电状态(State of Charge,SOC)基础上提出风储控制策略,此方案结合风力发电机桨距角的功率调节能力与储能系统的快速响应能力,提高了风电并网稳定性,为本文选取桨距角控制方法提供了借鉴.现有储能系统参与电网二次调频的控制策略包括:基于SOC实施功率分配,在满足储能系统总体功率调节需求的同时,确保各储能单元SOC满足预期目标[11];基于SOC采用部分储能单元以最优SOC运行,其他储能单元最大出力运行的方式实施功率分配[12].文献[13]中基于SOC对电化学储能系统的各单元进行控制,与风力发电机协调进行一次调频.这些策略都是分别考虑风力发电机和储能系统参与电网一次调频,没有对风场和储能系统统一进行二次调频,而且上述控制策略处理约束条件的能力较差,不具有最优性.模型预测控制(Model Predictive Control,MPC)是一种最优控制技术,可以很好地解决多约束条件下的优化问题.

综上所述,现有研究多关注风电场的一次调频,关于二次调频的研究很少.因此,合理解决风电场的频率控制问题,在兼顾稳定性的前提下使得风力发电机具备充足的二次调频能力,并且实现风电场和电化学储能系统协调参与电网二次调频,是需要进一步深入研究的内容.

通过分析风力发电机的机械特性和电化学储能系统的运行特性,利用风力发电机在桨距角减载运行方式下输出功率的可调性,本文建立基于风力发电机和储能系统参与电网二次调频的预测模型,提出一种基于MPC的风储联合电场参与电网二次调频策略.该控制策略在保证风电场支撑电网频率调整的基础上,更好地分配了风电场内各风力发电机的有功出力,避免风力发电机的桨距角过度变化,减少了风能损失.此外,该控制策略充分发挥了电化学储能系统的辅助调频能力,进一步减少了风能损失,保障了对电网频率的支撑.

1 双馈风力发电机参与电网二次调频控制方式

通常,风力发电机运行于最大功率跟踪模式,当电网频率发生跌落时,无法提供额外的有功功率支撑来参与电网二次调频.因此,风力发电机须采用减载措施以获取足够的有功备用[14].

桨距角控制的调节能力较强,调节范围也较大,可以实现全风速下的功率控制,而且变桨距控制系统可以提高风力发电机的风能利用率,可以减小阵风、载荷波动对风力发电机造成的影响,并与二次调频的时间尺度吻合.风电场运行在最大功率跟踪模式下,提供二次调频的功率裕量极少,因此为了实现风力发电机获得足够有功备用的目标,依据风力发电机所处的风速,采取设置初始桨距角的方法,使风力发电机运行于减载模式下.

双馈风力发电机通过调整桨距角和转速,可在较大风速范围内实现20%～100%额定容量的有功调节,调节范围如图1所示,其中v为风速,WTG表示风力发电机.

桨距角控制是在保持叶尖速比始终在最优值时通过调节风力发电机叶片桨距角,控制风力发电机捕获得到的机械能,从而实现风力发电机有功功率控制.图2为桨距角控制下风力发电机的运行点变化过程,其中Pm为机械功率,ωr和ωmax为转子转速及其最大值,θ1～θ4为风力发电机桨距角.当风力发电机工作于最大功率跟踪模式时,风力发电机工作于运行点A,对应桨距角为0°,捕获的机械功率为Pmax.当风力发电机的有功控制指令下降至Pcmd1、Pcmd2和Pcmd3时,风力发电机应上升桨距角使得其捕获的机械功率下降,对应的运行点为B、C、D.当风力发电机有功控制指令在Pmax与Pcmd3之间时,风力发电机应工作于曲线ABCD上,且所有调节过程均为可逆.

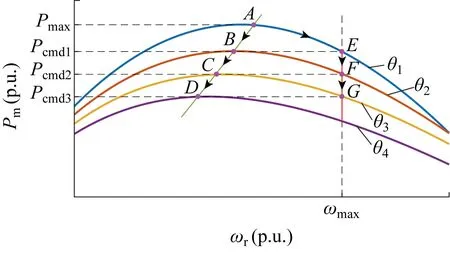
图2 恒定风速下风力发电机机械功率曲线

由上可知,可通过调整桨距角来改变风能利用系数,这种控制方式能够稳定地改变风力发电机输出功率,从而为二次调频提供有功支撑.本文建立基于桨距角控制的风电场的预测模型和储能系统的预测模型,在控制过程中,MPC控制器收集来自各个风力发电机和储能系统的测量值,预测其动态变化,并调节风力发电机和储能系统的有功功率输出,以实现控制目标.根据上级系统的有功功率指令值和风力发电机实际输出功率之间的差值对桨距角控制进行修正,使得风力发电机在二次调频期间能够更好地调整桨距角来改变风力发电机出力,以此达到上级系统的功率指令值.

2 风储联合电场的预测模型

2.1 风力发电机的模型

根据空气动力学模型,风力发电机捕获的机械功率为

(1)

λ=wrR/v

(2)

式中:ρ为空气密度;θ为桨距角;R为风轮机半径;λ为叶尖速比;Cp为风能利用系数,可表示为[15]

(3)

考虑桨距角控制时,在风速变化的同时,风力发电机转速也随之变化,叶尖速比在小范围内变化,因此可以将叶尖速比设为定值.对式(3)进行简化,得到Cp关于θ的数学表达式:

Cp=0.22 (1 450θ-1-4.06θ-3-

0.4θ-5)e-12.5(12.5θ-1-0.035θ-3)

(4)

将式(4)代入式(1),可得:

0.4θ-5)e-12.5(12.5θ-1-0.035θ-3)]

(5)

当风电场处于中高风速下采取桨距角控制时,调频的时间尺度较短,为了简化模型,设定风速一直保持在某个较高的值不变.当风速一定时,可以得到风力发电机捕获的机械能和桨距角近似的线性关系为[16]

Pm=k0θ+b

(6)

式中:k0为线性关系的系数;b为常数.

在一个桨距角控制周期内,桨距角可表示为

θ=θ0+Δθ

(7)

式中:θ0为初始桨距角;Δθ为桨距角变化量.

进而式(6)可以表示为

ΔPm=k0Δθ

(8)

式中:ΔPm为风力发电机机械功率变化量.

风力发电机桨距角控制的响应较缓慢,其传递函数可等效为一阶传递函数,即

Gθ(s)=1/(1+Tθs)

(9)

式中:Tθ为桨距角控制响应时间常数;s为自变量.

进而可以得到Δθ和桨距角变化量参考值Δθref之间的关系:

Δθ=ΔθrefGθ(s)

(10)

风力发电机内部损耗等问题导致风力发电机捕获的风能不能全部转化为电磁功率,两者之间的转化关系可以用一阶传递函数表示:

(11)

式中:ΔPe为电磁功率变化量;T为时间常数.

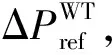
(12)

风场内的每台风力发电机i的预测模型可以表述为

(13)

(14)

(15)

式中:Ai、Bi、Ci为参数矩阵;Δxi为状态变量矩阵;Δyi为输出变量矩阵,包括桨距角、风力发电机机械功率、电磁功率的变化量;Δui为控制变量矩阵,包括桨距角和电磁功率变化量参考值.

2.2 储能系统的模型

为研究储能系统分配的调频功率与储能单元SOC的关系,建立储能系统的预测模型.在充放电过程中储能单元的SOC一直变化,可由下式表示:

(16)

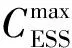
(17)

(18)

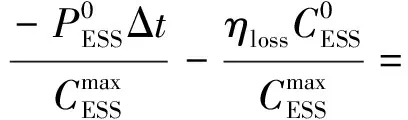
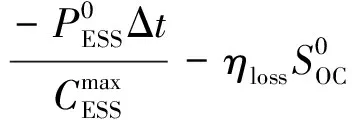
(19)

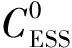
(20)

(21)

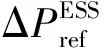
(22)

(23)

(24)

式中:AE、BE、CE和EE为储能系统的参数矩阵;ΔxE为储能系统的状态变量矩阵;ΔyE为储能系统的输出变量矩阵,包括电池SOC、储能系统输出功率的变化量;ΔuE为储能系统的控制变量矩阵,包括储能系统的输出功率变化量参考值.

2.3 风储联合电场的模型

基于风力发电机和储能系统的模型,风储联合电场的连续状态空间模型可以表述为

(25)

(26)

式中:A、B、C和E为风储联合电场的模型的参数矩阵;下标NC和E分别表示风电机组的数目和储能系统.

基于连续状态空间模型,转化为采样时刻为ΔTP的离散时域状态空间模型:

(27)

(28)

式中:G和H为离散时域状态空间模型的参数矩阵;Δu(k)为k时刻的控制变量.

3 基于MPC的调频优化控制策略

风电场在响应二次调频指令之前,需要保持减载运行模式,留有足够的有功备用,故风电场中各风力发电机根据所处位置的风速以不同初始桨距角运行.在二次调频过程中,如果风电场控制器向风力发电机调度相同的有功功率指令值,会出现桨距角变化过大情况,造成更多风能资源损失.因此需要优化各风力发电机的有功分配,设计合适的控制策略.在此基础上,为了进一步减少风能损失,减小桨距角变化量,引入储能系统减少风力发电机的减载备用功率,提出一种基于MPC的优化分配控制策略.

3.1 MPC控制原理

MPC是一种应用广泛的控制方法[19-22],在每一个采样时刻,根据获得的当前测量信息,在线求解一个有限时间开环优化问题,并将得到的控制序列第一个元素作用于被控对象.在下一个采样时刻,重复上述过程,用新的测量值作为此时预测系统未来动态的初始条件,刷新优化问题并重新求解,MPC的原理如图3所示,t0为初始时间.为了准确预测风电场的动态变化,需要设置合适的控制周期Tc和预测周期Tp.控制周期要小于预测周期,而且大于采样时间间隔ΔTP,预测周期由风电控制系统的动态性能决定.

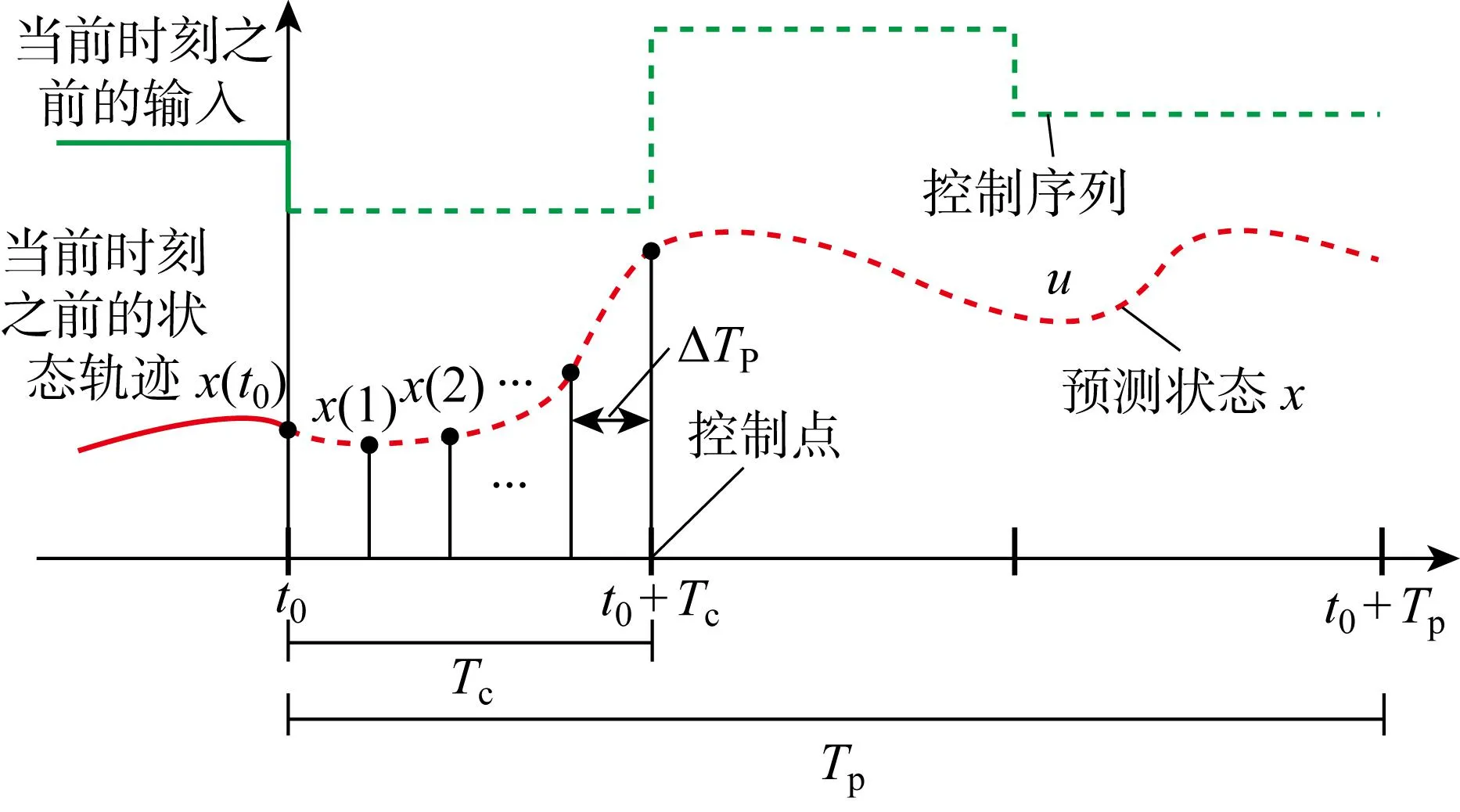
图3 模型预测控制的原理

3.2 MPC优化策略

建立基于MPC的桨距角控制策略的优化问题,包括约束条件和目标函数.第1个控制目标为最小化风力发电机之间桨距角的差距以保证风电场中每一台风力发电机的稳定运行.在只采用第一个控制目标的情况下,即风力发电机之间的桨距角差异最小化,这意味着所有风力发电机的桨距角都收敛到同一值.第2个目标函数为减小风力发电机自身的桨距角变化量,目的是最大限度地减少风能损失[8].第3个目标函数为使储能系统留有足够的充放电功率裕量,结合储能电池SOC,基于SOC初始值、实际充放电时间和SOC期望值等,可以维持储能电池在较好的SOC内,有效改善调频效果,且在一定程度上降低了储能电池辅助调频的容量配置需求,对储能电池规模化应用到电网调频中具有一定意义[23-24].

风电场的两个目标函数分别为

(29)

(30)

电化学储能系统的目标函数为

(31)

总的目标函数是风场和储能系统的目标函数按照权重系数划分后相加:

(32)

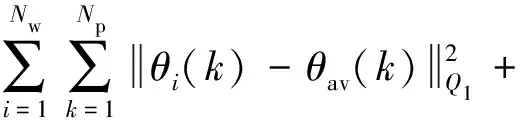
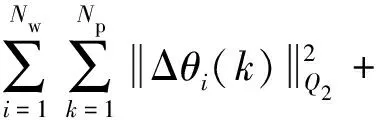
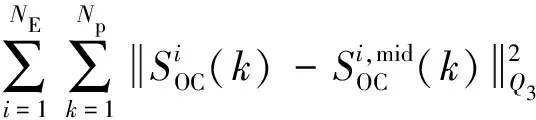
(33)

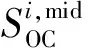
(34)

(35)

(36)

(37)

3.3 桨距角结构的改进

为准确达到上级系统的功率指令值,采用桨距角修正方案,通过引入桨距角补偿值,使风力发电机能响应频率变化达到上级系统下达的指令值.采用如图4的控制结构,简化了利用桨距角进行调频的控制方案.

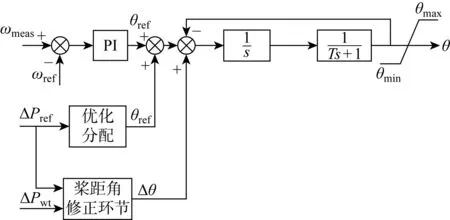
图4 桨距角控制结构

传统桨距角的控制指令是转子的额定转速ωref和实际转速ωmeas,为了严格追踪上级下达的有功功率指令值,桨距角控制方案在传统桨距角控制的基础上添加了桨距角响应功率指令环节和桨距角修正环节,其中桨距角修正环节的控制指令是风力发电机的有功功率参考值ΔPref和实际输出的有功功率值ΔPwt.控制过程为:首先根据当前风速下的ΔPref值确定机组完成调频任务所需桨距角变化量参考值Δθref;由于模型的简化会产生误差,所以引入桨距角修正环节,然后根据当前风速下风力发电机的ΔPref和Δpwt的差值,确定桨距角修正量Δθ,从而调节风力发电机的桨距角值θ.

当需要风电场参与调频时,上级系统根据频率恢复至额定值所需的功率缺额给风电场下达有功功率指令值,使风电场在不影响到电网稳定的前提下对电网提供有功支撑,完成二次调频的任务.

4 案例分析

图5为典型风储联合电场的结构图,风电场经由33 kV/110 kV变压器,再由20 km、110 kV的架空线连接到外部110 kV的交流电网中.风电场由10台风力发电机、两条馈线组成,每条馈线上连接5台额定容量为5 MW的风力发电机,并且每台风力发电机之间的距离为2 km.风场中每台风力发电机的风速为13 m/s,初始桨距角为5°,电化学储能系统的储能容量为5 MW,二次调频功率参考值为35 MW.

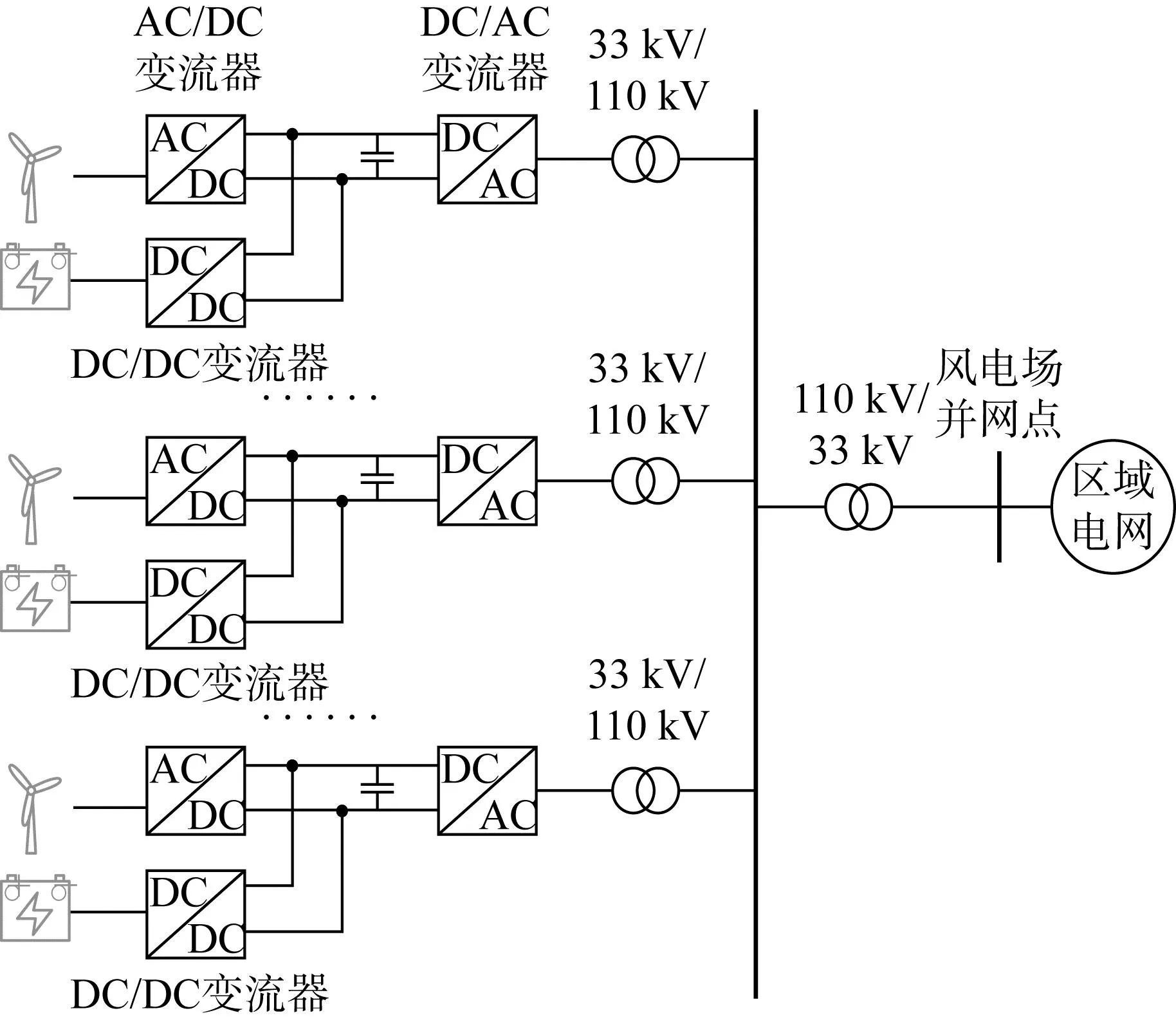
图5 风储联合电场结构

图6为在平均分配策略下,风电场内每台风力发电机分配到上级系统发出的有功功率追踪指令值均为0.7(p.u).图7为平均分配策略下各风力发电机的桨距角参考值,由于上级系统发给每台风力发电机的有功功率指令值是相同的,所以风力发电机的桨距角均将收敛至同一值.

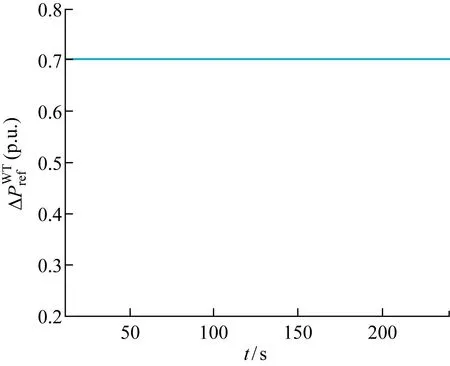
图6 平均分配策略的各台风力发电机的功率指令值

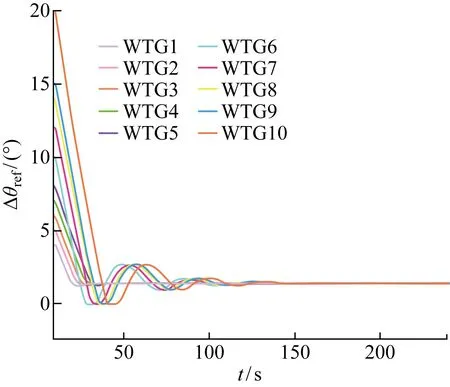
图7 平均分配策略下的桨距角参考值

图8为风电场在接受到上级系统下达的有功功率追踪指令值后,根据不采用MPC的一步优化分配策略得到各风力发电机所分配的有功功率指令值,此时功率指令值根据优化策略中目标函数1和目标函数2得到.图9为各风力发电机在一步优化策略下的桨距角参考值.

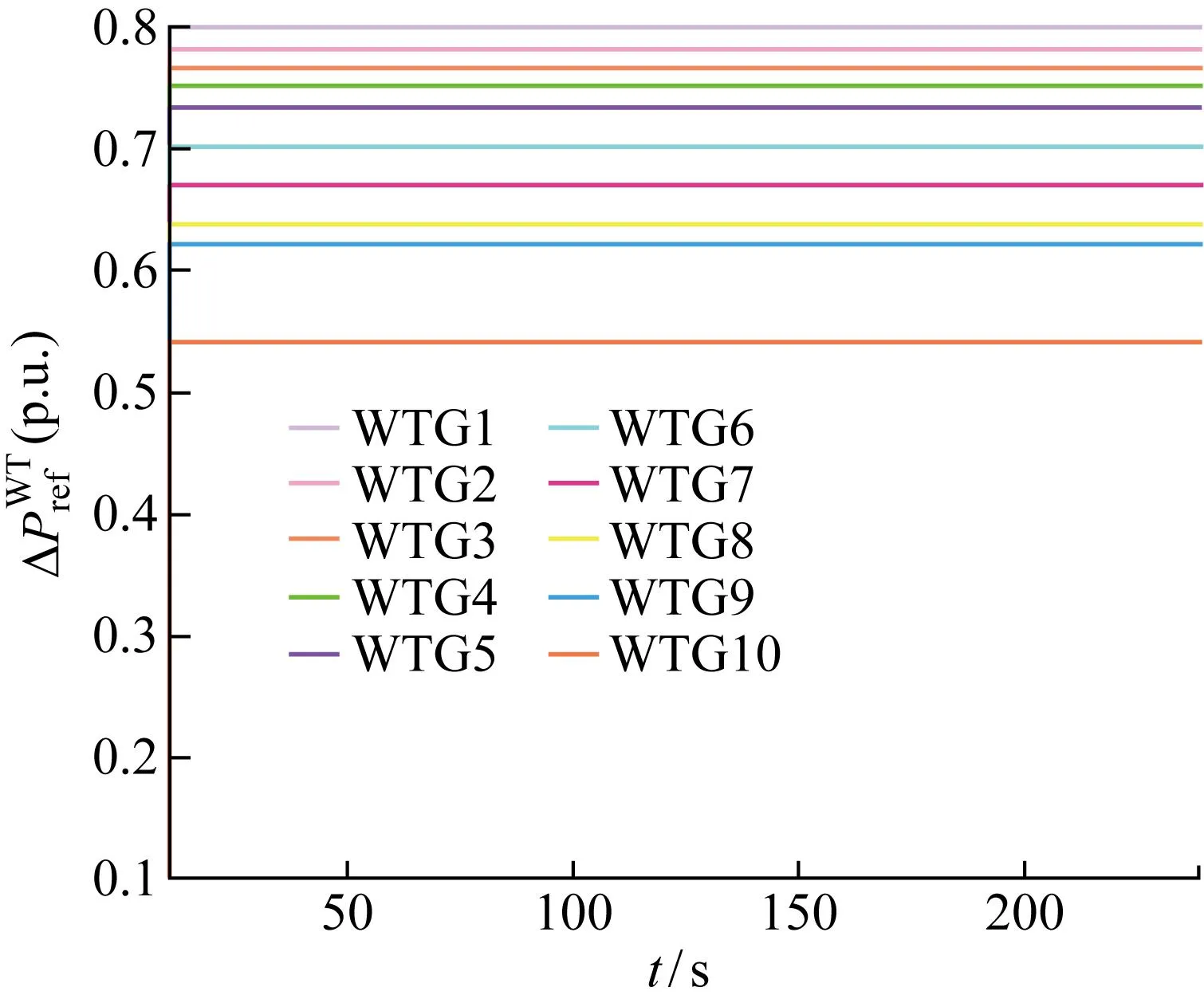
图8 优化分配策略下的风力发电机有功功率指令值

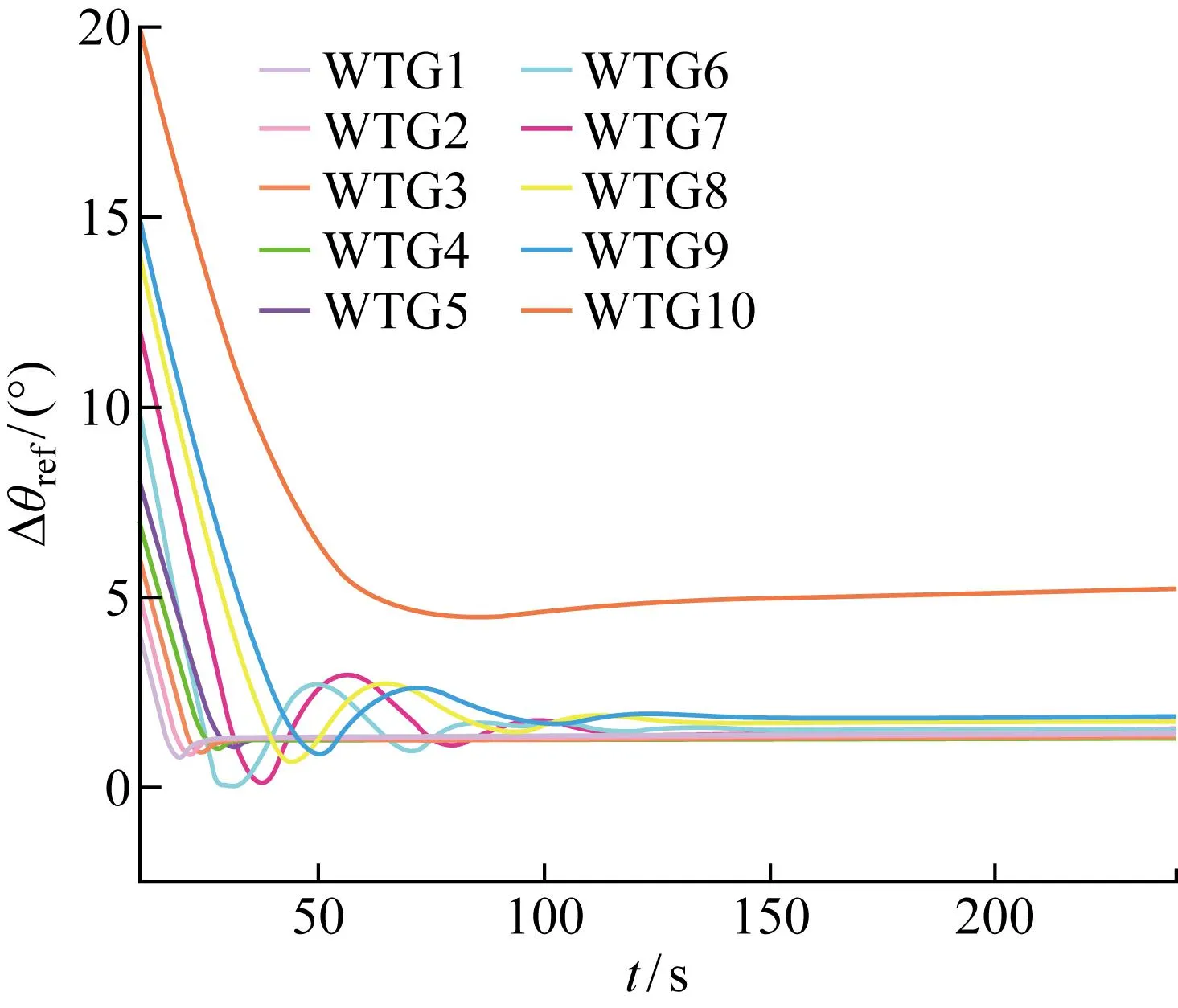
图9 优化分配策略下的桨距角参考值

图10和图11分别为基于MPC优化策略当不考虑储能系统时风电场各风力发电机的有功功率参考值和桨距角参考值.

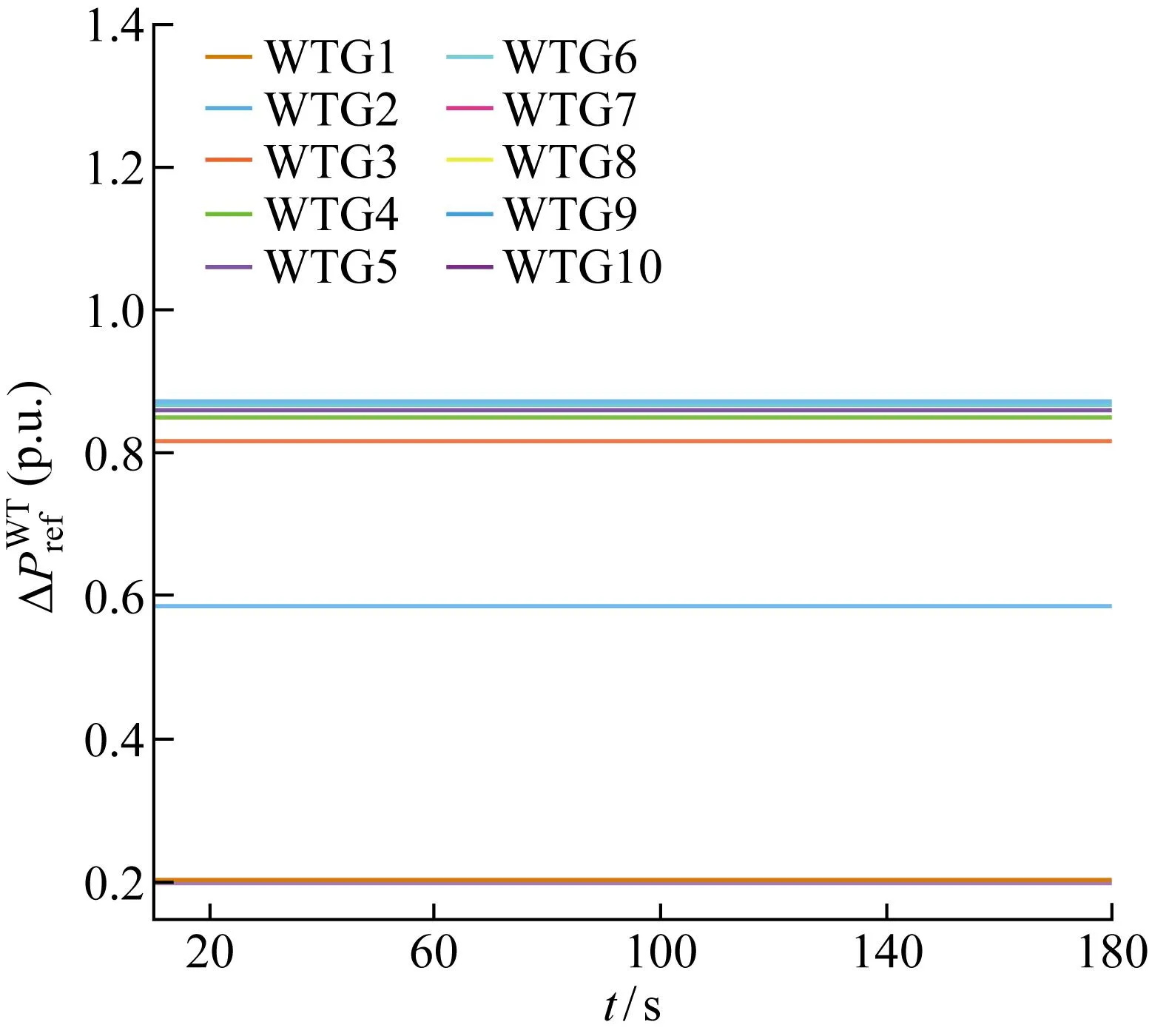
图10 基于MPC不含储能的风电场优化策略的有功功率参考值

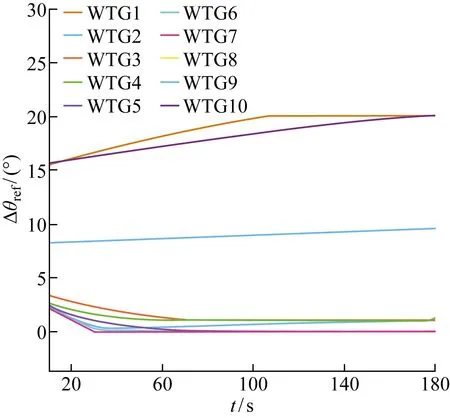
图11 基于MPC不含储能的风电场优化策略的桨距角参考值

因为电网下发的功率指令值超过储能系统的容量,所以需要风电场和储能系统联合参与电网的二次调频,此时3个目标函数的权值设置为:Q1>Q3>Q2.图12和图13分别为在基于MPC含储能风电场优化策略下有功功率参考值和风力发电机的桨距角参考值,图14为基于MPC优化策略的储能系统有功功率值.由图14可知,储能系统留有足够的充放电功率裕度,由于储能系统的变流器响应时间常数比风力发电机变桨结构响应时间常数更小,所以储能系统的响应速度比风力发电机更快.

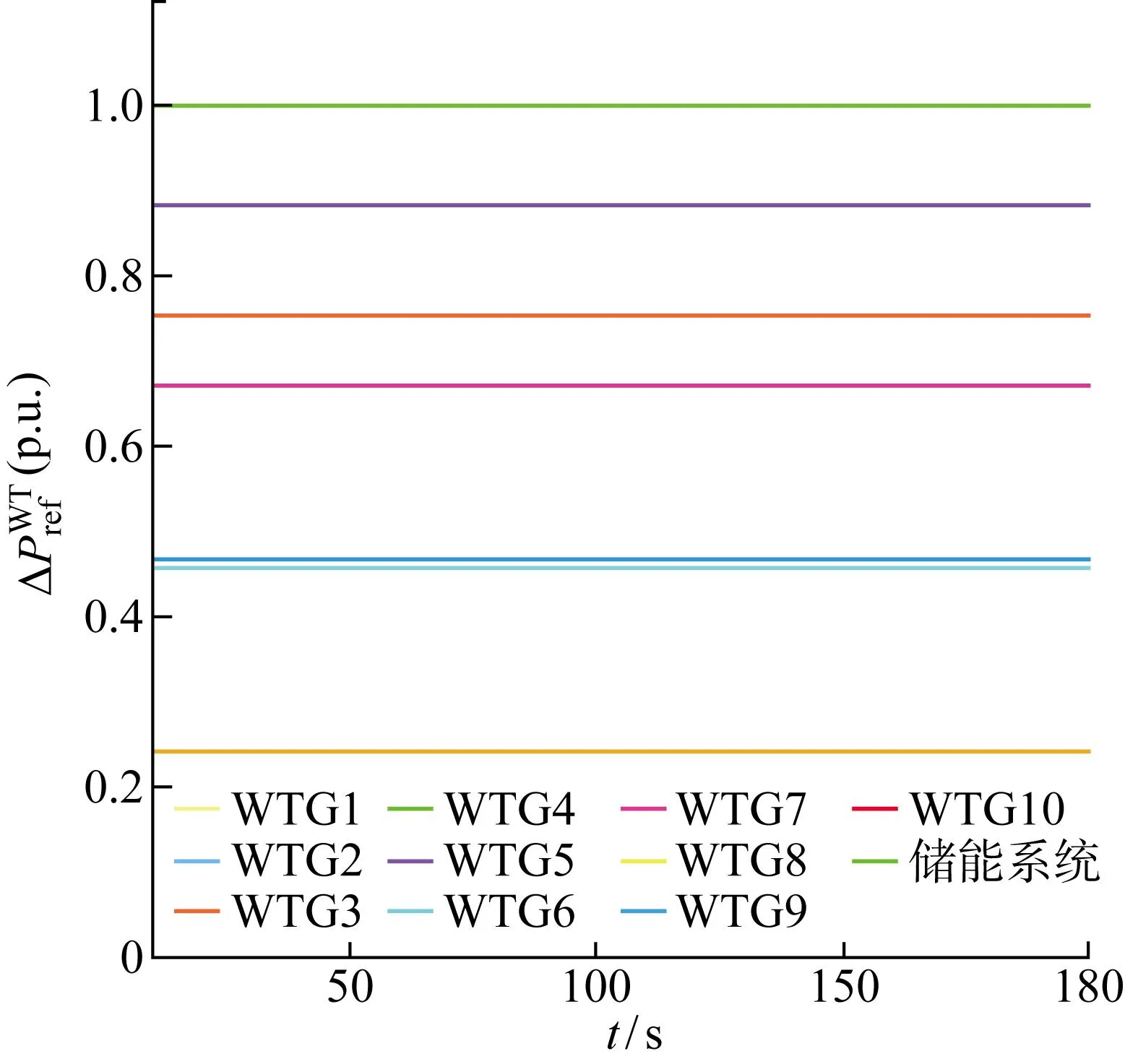
图12 基于MPC含储能的风电场优化策略的有功功率参考值

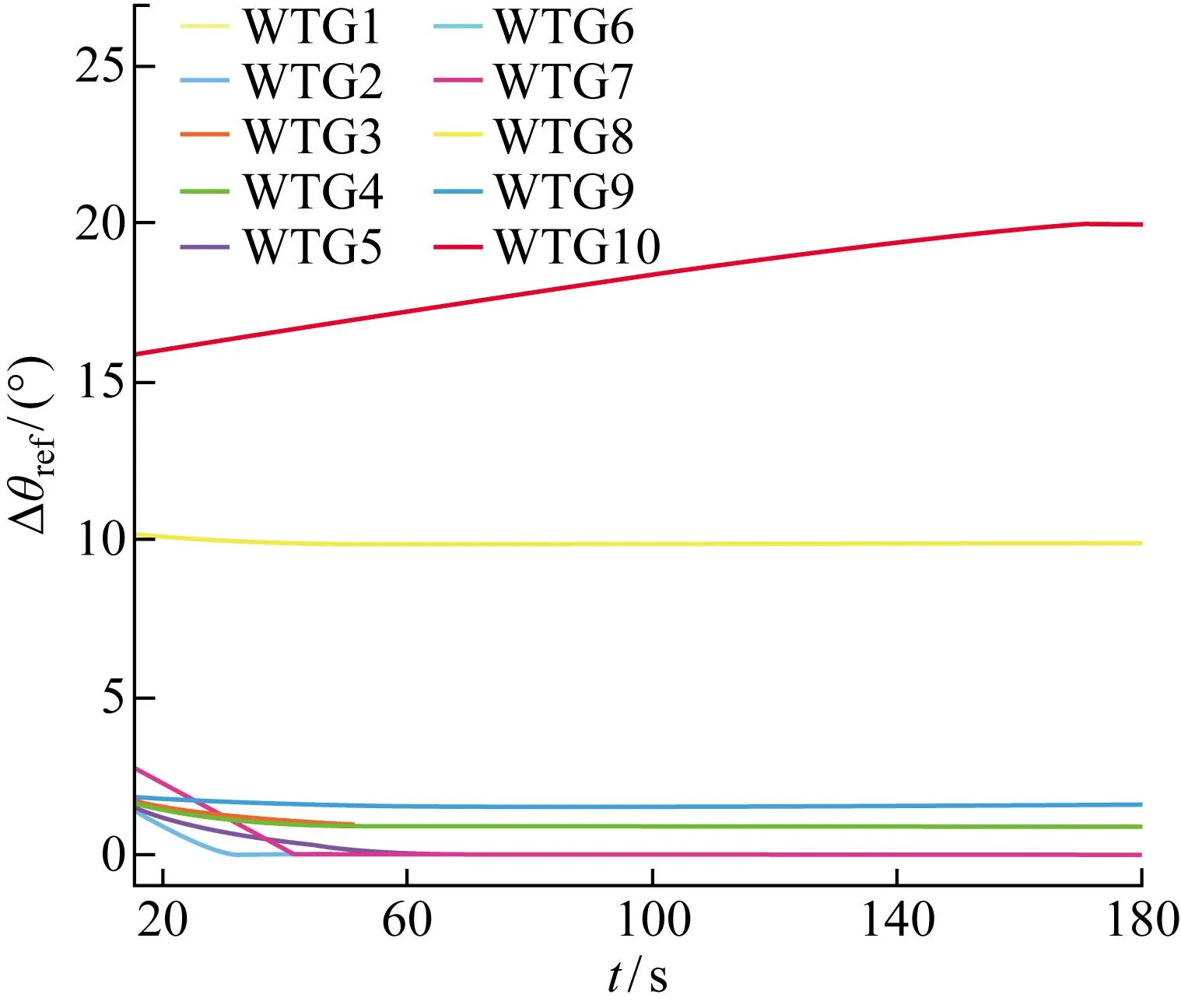
图13 基于MPC含储能的风电场优化策略的桨距角参考值

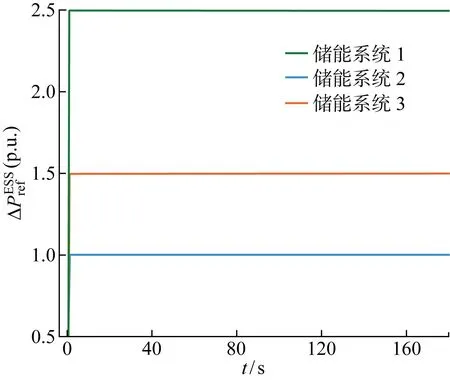
图14 基于MPC优化策略的储能系统有功功率

根据图15可知,基于MPC含储能优化策略的桨距角变化量不仅少于平均分配策略和一步优化策略下的桨距角变化量,同时还少于基于MPC不含储能风电场优化分配策略下的桨距角变化量.在基于MPC含储能风场的优化分配策略下,储能系统快速响应、精确跟踪的能力减少了桨距角的变化量,节省了调节时间,加快了控制速度,进而减缓了桨距角机械机构的损耗.而在图16中的仿真结果可以看出,风力发电机采用平均分配、一步优化分配、基于MPC不含储能风电场的优化分配和基于MPC含储能风电场的优化分配策略追踪到功率参考值用时分别为120 s左右、100 s左右、80 s和50 s,基于MPC含储能风电场的优化分配控制策略达到指令值速度更快的同时功率追踪过程比其他3种策略的功率追踪过程更加稳定.

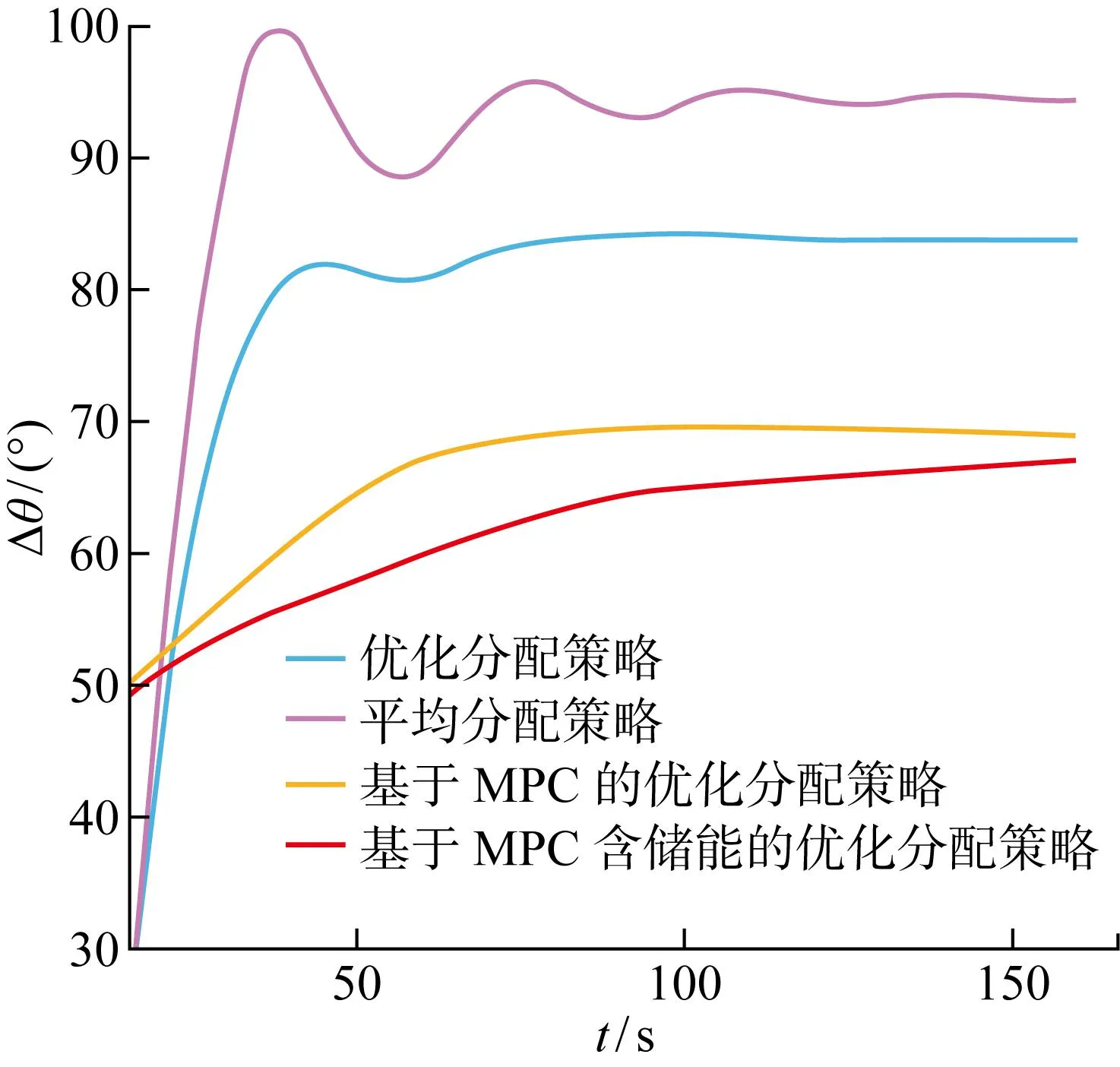
图15 四种的桨距角变化量

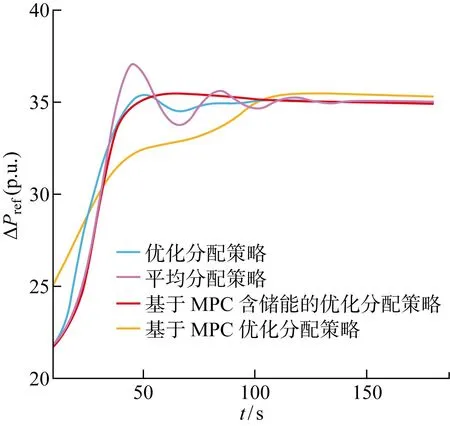
图16 四种策略有功功率追踪结果

5 结语

提出一种基于MPC的风储联合电场参与二次调频控制策略,利用风力发电机可控的二次调频能力和储能系统快速响应、精确跟踪的特性,优化风电场内储能系统以及各风力发电机的有功分配.仿真结果表明,与传统有功功率参考值平均分配策略和一步优化分配策略相比,本文基于MPC含储能的桨距角优化策略可以更好地追踪上级系统下达的有功功率指令值,避免风力发电机的桨距角过度变化,实现最小化风能损失的目标,更好实现风储联合电场完成二次调频的任务.