直动式机电运动装置的改进磁路-运动耦合模型及快速仿真

江 鹏, 关振群, 赵国忠, 张 群, 秦志强

(1.大连理工大学 工程力学系,辽宁 大连 116024; 2.英特工程仿真技术(大连)有限公司,辽宁 大连 116023; 3.大连工业大学 艺术与信息工程学院,辽宁 大连 116400)

有限元方法和等效磁路方法已被广泛用作电磁系统优化设计的工具[1].有限元方法具有计算精度高、适用于复杂几何结构和非线性问题的优点,但是在计算较大规模的问题时,求解效率较低,往往不能适应机电装置动态性能的快速评估和优化设计的需求[2-5].等效磁路方法[6-12]通过集总参数将复杂的系统简化为简单的数学模型,具有求解速度快、易于实现的优点,但它可能缺乏准确性,难以应用于一些具有复杂几何形状的模型,无法给出磁场的具体分布,常常局限于近似分析中.磁阻网络法[13-18]是在等效磁路模块基础上发展而来适用于电磁机构分析和优化的方法,该方法保持了磁路法求解速度的优势,但是为了准确计算漏磁需要建立较复杂的磁阻网络模型[19].

等效磁路法和有限元法具有优势互补的特点,因此空间映射技术综合了磁路法和有限元法的优点,通过建立磁路模型与有限元模型间的映射关系,实现模型的快速计算[20-23].翟国富等[2]将空间映射方法首先应用在继电器上,通过有限元模型数据修正磁路法的结果,在保证计算精度的同时提高了计算效率,并采用遗传算法对电磁继电器的动态特性进行优化.Yang等[24]在此基础上针对继电器设计提出一种基于补偿矩阵的快速算法,该方法使用二维补偿矩阵,对不同衔铁位移、线圈电流下磁路法计算忽略的漏磁和饱和进行修正,具有计算速度快和精度高的特点.

文献[2,24]中基于空间映射原理的电器快速仿真算法具有较广泛的通用性,有效综合了磁路法和有限元法的各自优势,可以应用于一般电器产品的快速计算和优化设计.但是对于固定几何结构、未磁饱和的电磁阀和继电器等电器,还可以通过改进磁路模型的磁阻假设,在大幅减少有限元数值仿真次数的同时,获得高精度的非饱和磁路模型,从而实现高效、准确的电器产品仿真计算.常规等效磁路模型常对铁芯和气隙的磁阻采用理想假设,虽然能解释机电运动机构所受到的磁吸附效应,但是难以准确预测实际的仿真结果.本文在磁路模型中采用机构运动位移的3次多项式表示总磁阻,并通过上、下运动极限处的静态磁力和电感值标定4个待定系数;改进的磁路模型可更加准确地预测磁吸力和电感随机构运动位移的变化,进而联合机电装置的机构运动方程,实现电磁制动器、电磁阀等机电运动装置的准确快速动态仿真.

1 直动式机电运动装置的磁路-运动耦合模型

图1所示为单边励磁的直动式机电运动装置简化模型[25],包含了机电系统的基本元件,即外端电系统、机电能量转换系统和外端机械系统.在该模型中,外端电系统由电压源U和电阻R串联而成,该电阻R包括机电能量转换系统自身电损耗在内的所有电损耗,如电压源的等效电阻、机电能量转换系统的绕组电阻等;e为电端口处的电压即线圈感应电势.设机械系统的机构运动位移x范围为x1≤x≤x2,其中x1和x2分别为运动位移上、下极限.在机电能量转换系统中,常设有气隙结构,能量通过气隙的开合实现转换.

考虑机电装置中的电磁-运动耦合问题,该机电装置中的电路方程[25]为

(1)

式中:λ为磁链;i为线圈电流;Lw为线圈自感;t为时间.该机电装置中的机械系统简化为一个劲度系数为K的弹簧和一个质量为M的质量块,所受到的磁力为Fm,则机械系统的动力方程[25]为

(2)

式中:x0为弹簧在自然松弛状态下的x值.引入速度变量v,将电磁运动耦合系统的微分方程式(1)和(2)表示为积分形式[25],得到:

(3)

根据式(3),对于任意输入电压U,可以求解出结构运动位移x和线圈电流i等.

2 多项式表示总磁阻的改进模型

在直动式机电运动装置模型中,参照文献[25],线圈自感Lw和机构所受磁力Fm可表示为

(4)

式中:N为线圈匝数;Rt(x)为非饱和磁路的总磁阻;Rc(x)为铁芯磁阻;Rg(x)为气隙磁阻.当机构运动位移x变化时,运动气隙边缘及相邻铁芯端部的磁场变化一般较为复杂,Rc(x)往往不是常值,Rg(x)与气隙厚度或运动位移x也不满足简单的线性关系.为了更加准确地预测Fm和Lw随x的变化规律,对Rt(x)采用x的n次多项式表示为

Rt(x)=(A+Bx+Cx2+Dx3+…)ν0

(5)

式中:A、B、C和D等为多项式的待定系数,其中A为机构初始状态(运动位移为0)时的磁阻,Bx为磁阻的线性变化部分,Cx2+Dx3+…表示运动位移引起磁阻变化的高阶量;ν0为空气磁阻率常数,作为多项式的比例因子.将图2(a)中分布的铁芯磁阻和气隙磁阻集中为式(5)中多项式表示的总磁阻Rt(x),得到图2(b)的磁路模型.

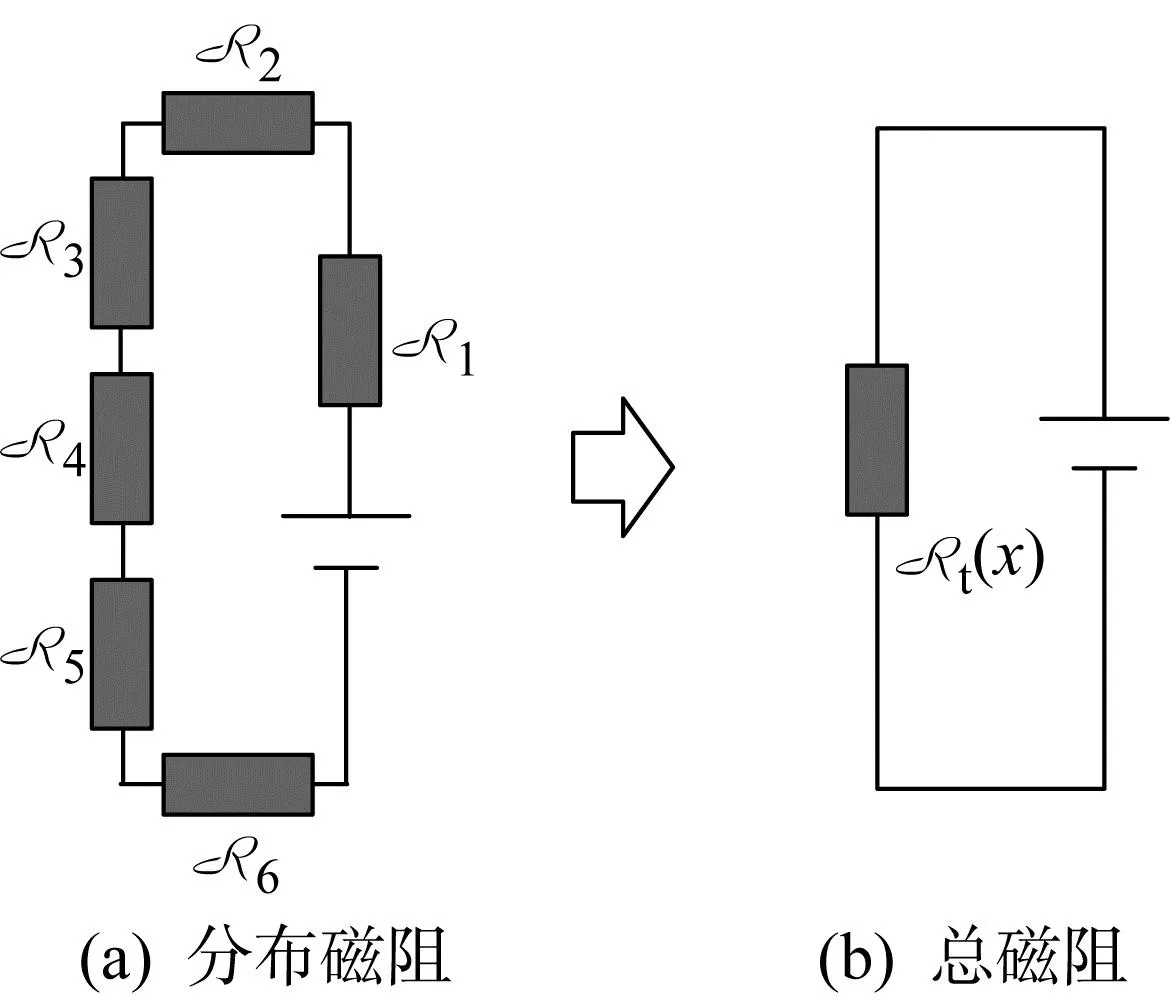
图2 直动式机电装置的磁路模型

由式(4)和总磁阻表达式(5),Lw和Fm可以进一步表示为

(6)

(7)

由式(6)和式(7)可知,可利用不同位移x处的线圈电感Lw或机构所受磁力Fm的仿真值标定系数A、B、C、D等.虽然式(5)中多项式的阶次越高,对总磁阻的拟合精度也越高,但是过高的阶次对改善精度的作用较小,同时,过多的待定系数需要较多的数值仿真进行标定.本文限定式(7)中的多项式阶次n≤3,且仅利用直动式机构在运动上、下极限处的静态线圈电感和磁吸力的仿真值标定待定系数.Lw(x1)和Fm(x1)是对应x1的电感和磁力数值仿真解,分别简记为L1、F1;Lw(x2)和Fm(x2)是对应x2的电感和磁力数值仿真解,分别简记为L2、F2.

当选择多项式次数n=1时,式(5)中的总磁阻是机构运动位移x的1次多项式:

Rt(x)=(A+Bx)ν0

(8)

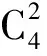
当选择多项式次数n=2时,总磁阻是机构运动位移x的2次多项式:

Rt(x)=(A+Bx+Cx2)ν0

(9)

当选择多项式次数n=3时,总磁阻是机构运动位移x的3次多项式:

Rt(x)=(A+Bx+Cx2+Dx3)ν0

(10)

由于可利用的标定值有4个,所以仅有1种标定方式,需要利用全部L1、F1、L2、F2来标定系数:

(11)

相比1次和2次多项式磁阻模型,3次多项式磁阻模型可以表示机构运动引起的更复杂的磁阻变化,同时3次多项式磁阻模型充分利用上、下运动位移极限处的静态线圈电感和磁力仿真值标定未知系数,因而一般具有更高的精度.

3 基于改进3次磁路-运动耦合模型的快速仿真

非饱和磁阻多项式的系数由静态线圈电感和机构所受磁力确定,可适用于直动式机电运动装置不同运行工况的动态分析.将式(10)中改进的磁阻Rt(x)代入式(6)可得到改进的电感Lw(x)和电感梯度dLw(x)/dx,进一步代入式(3),可得到改进的磁路-运动耦合模型.基于改进的3次磁路-运动耦合模型仿真流程如图3(a)所示,主要包括以下几个步骤:首先,采用数值仿真手段获得运动位移上极限处x1的磁力F1和电感L1,以及运动位移下极限处x2的磁力F2和电感L1;然后,利用两个运动极限处的磁力和电感仿真值,根据式(11)计算式(10)中的系数A、B、C和D,从而确定Lw(x)和dLw(x)/dx的表达式;最后,通过搭建的Simulink系统计算动态特性方程(3),并绘制i和x等变量的时间历程曲线.图3(b)为动态特性方程(3)在Simulink系统中的实现,图中的3个积分器分别对应式(3)中的3个积分方程.

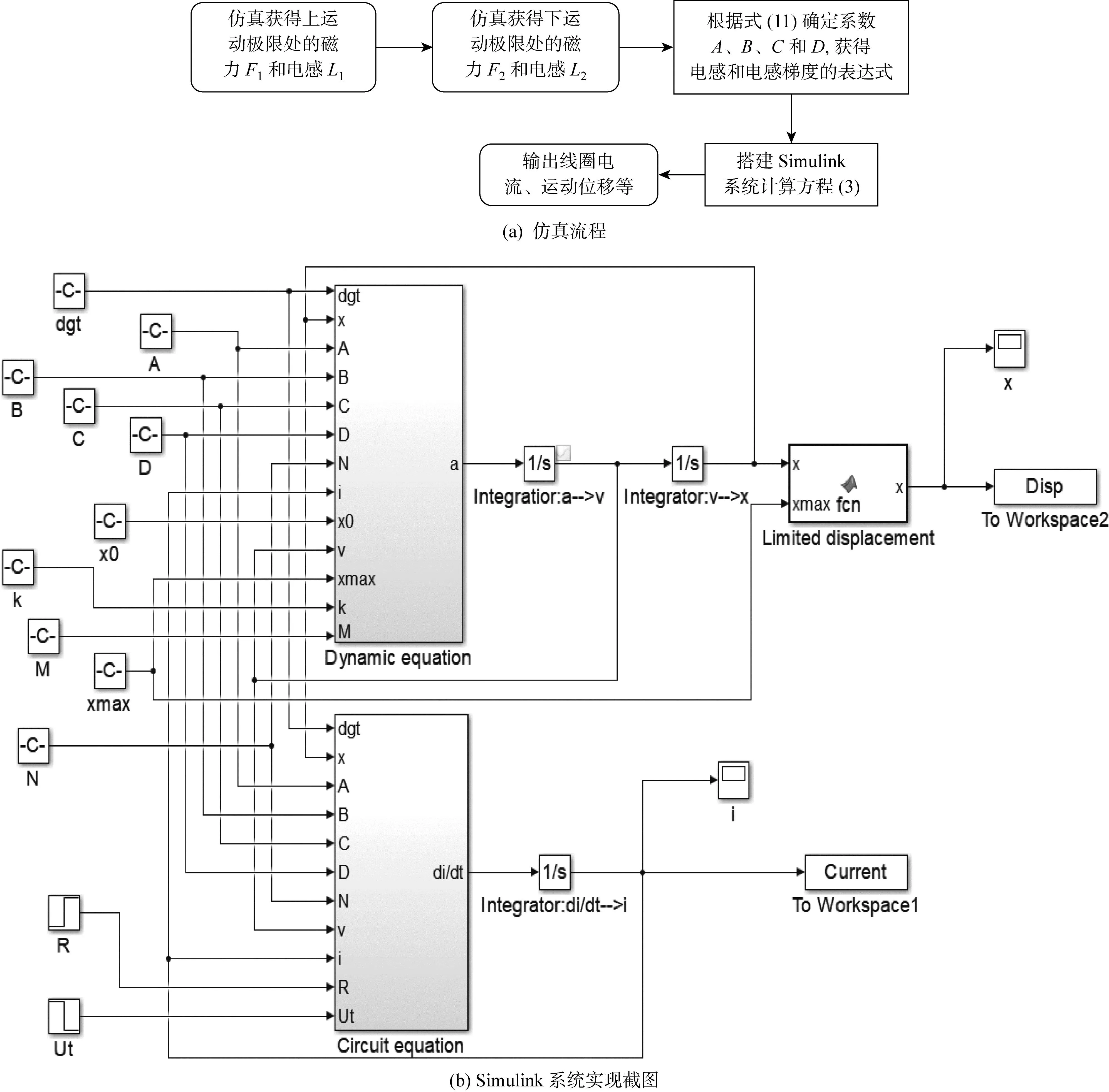
图3 基于改进磁路-运动耦合模型的快速动态仿真流程

4 算例验证

4.1 电磁制动器动态特性的快速仿真

图4所示为制动器主体的轴对称几何模型和外电路.在图4(a)的主体结构中,上端运动衔铁与弹簧相连,衔铁下方为静止的护铁.定义衔铁向上运动为正方向,当衔铁与护铁接触时位移为0,并限定衔铁的运动上、下极限位移分别为0.5和2.5 mm,衔铁初始位移为2.5 mm.在图4(b)的电路模型中,绞线圈作为电路中的一部分,与24 V的电源及开关构成回路,并与续流电阻和二极管并联,续流电阻Rf为100 Ω.绞线圈匝数N为2 548,线圈电阻Rw为50 Ω,衔铁和护铁的相对磁导率分别设为 2 000 和 1 000,衔铁质量M为0.25 kg,弹簧劲度系数K为1 kN/m,初始拉伸长度为0.01 m.仿真总时长为0.2 s,开始时电源开关闭合,在0.1 s时断开.

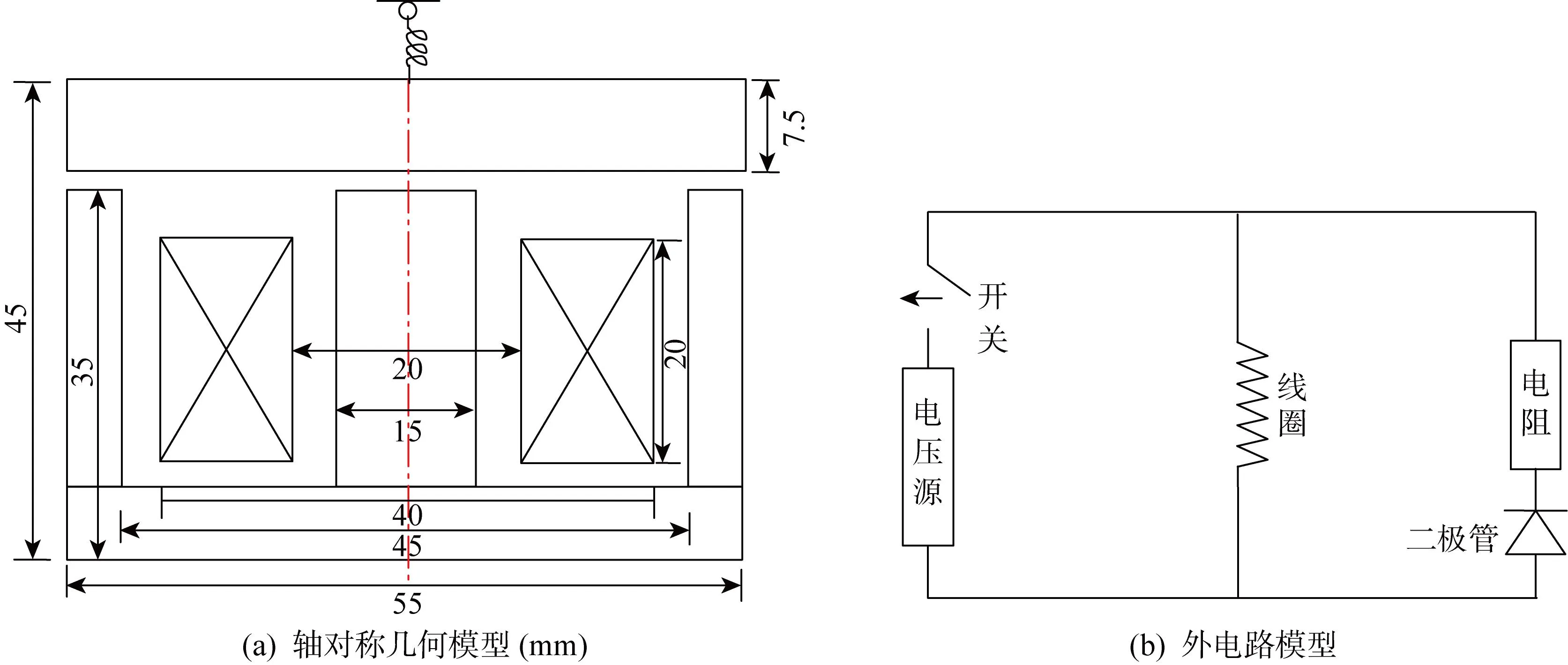
图4 电磁制动器轴对称几何模型和外电路模型

在对该电磁制动器进行动态仿真前,对比数值模型和不同磁路模型计算得到的磁力和电感随气隙厚度变化曲线,验证改进的3次磁路模型具有较高的精度.设定线圈稳态电流大小为0.48 A,利用上、下运动极限处静态电感和磁力的数值仿真结果标定不同阶次总磁阻磁路模型的待定系数,得到表1中的待定系数值.图5对比了理想磁路模型、改进的磁路模型以及有限元模型计算得到的磁吸力和电感随气隙厚度或运动位移的变化曲线.其中有限元模型采用三角形网格划分,网格总数为 3 708,当衔铁运动时,气隙网格会发生挤压变形.可以发现,改进的3次磁路模型具有最高的精度,准确地预测了不同气隙厚度的磁力和电感的有限元仿真结果,说明3次多项式表示的总磁阻磁路模型充分考虑了气隙厚度变化引起的气隙边缘及铁芯端部磁场变化.

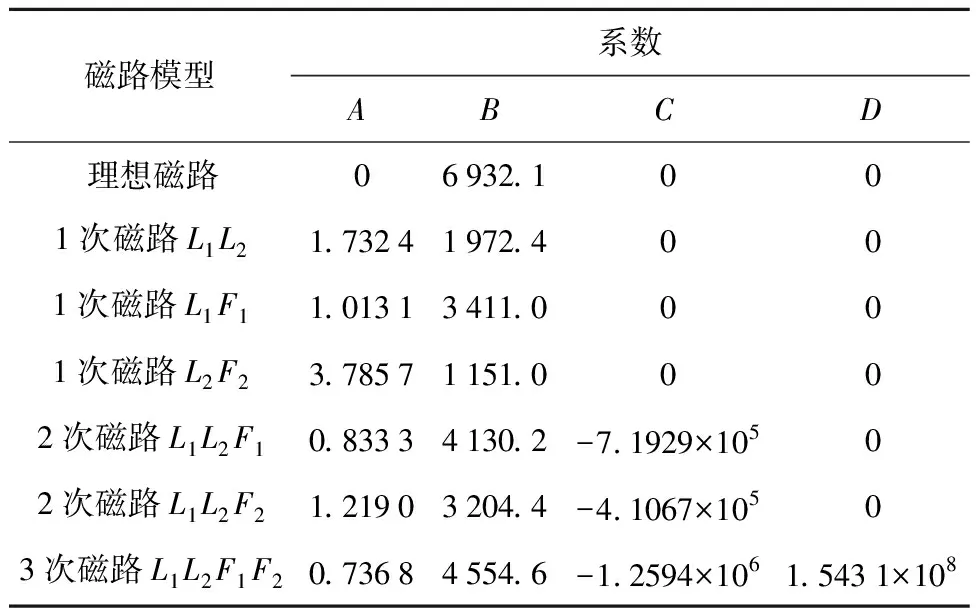
表1 电磁制动器磁路模型系数值

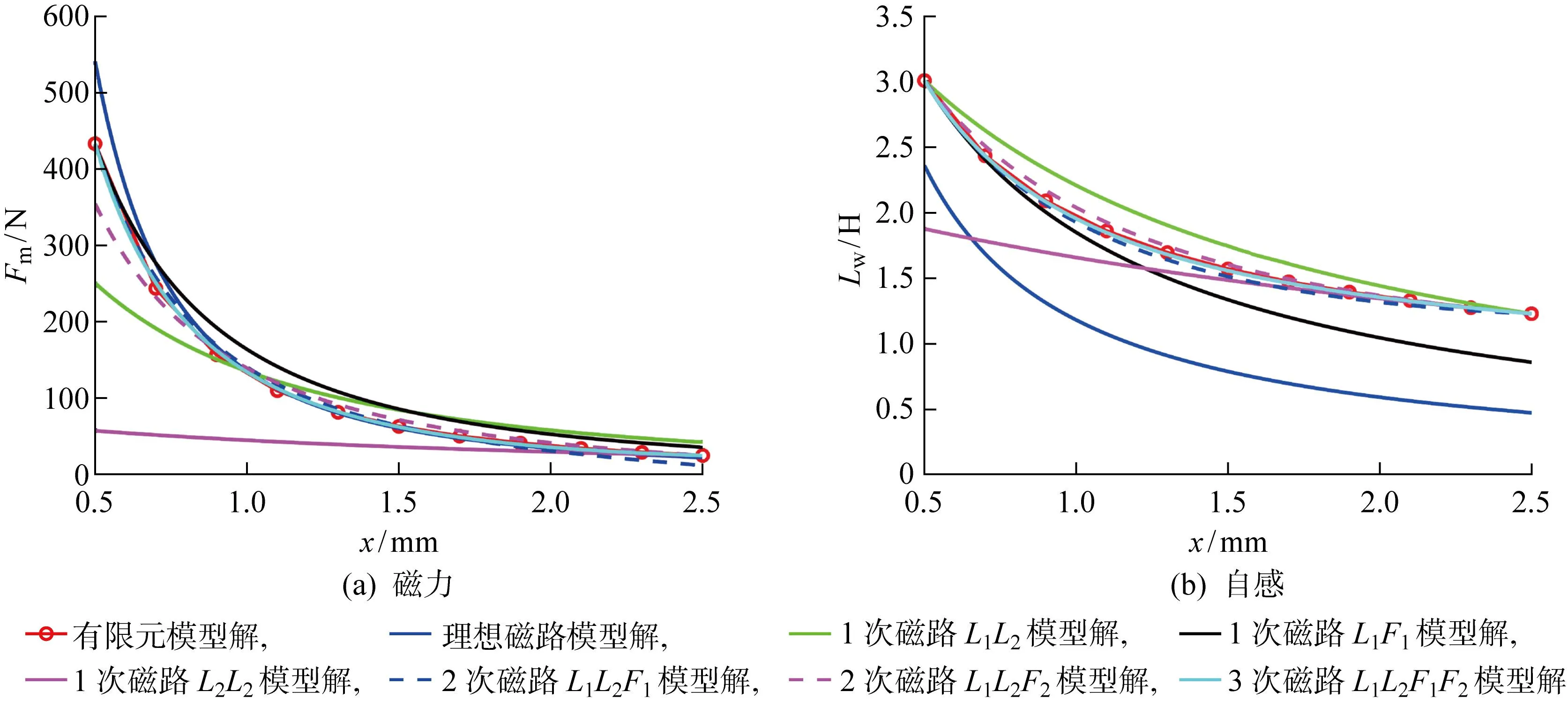
图5 电磁制动器中磁力与自感对比

利用不同阶次的磁路-运动耦合模型,在Simulink系统中对该电磁制动器的动态过程进行仿真.图6为线圈电流、线圈感应电势e、衔铁磁力及运动位移的时间历程曲线,并且与有限元-运动耦合模型的仿真结果进行对比,发现只有改进的3次磁路-运动耦合模型能够准确预测该制动器动态过程的各个输出量.此外,改进的3次磁路-运动耦合模型将有限元仿真所需的223 s缩短为1.6 s,大幅提高了电磁制动器动态特性计算的效率.

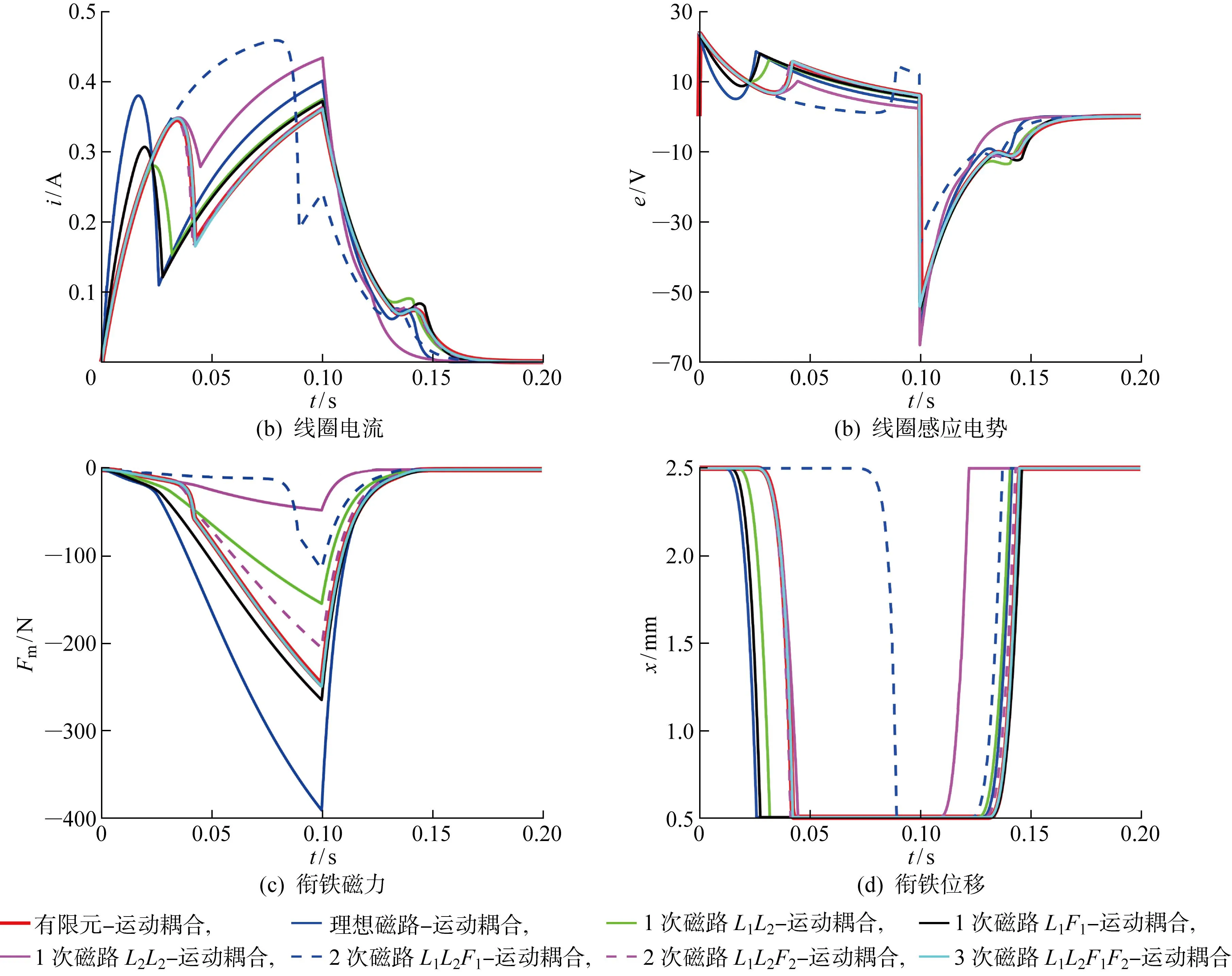
图6 电磁制动器中改进的磁路-运动耦合模型与有限元-运动耦合模型的结果对比

4.2 伺服阀动态特性的快速仿真

图7为某伺服电磁阀的轴对称几何模型示意图.铁芯材料的相对磁导率为 4 000,Rw为55 Ω.电磁阀外电路采用图4(b)中的电路模型,Rf为 100 Ω.在初始时刻打开开关,然后在0.05 s闭合开关,因此在0.05 s时,式(3)中的电压U从初始24 V变为0,电路总电阻R从55 Ω变为150 Ω.

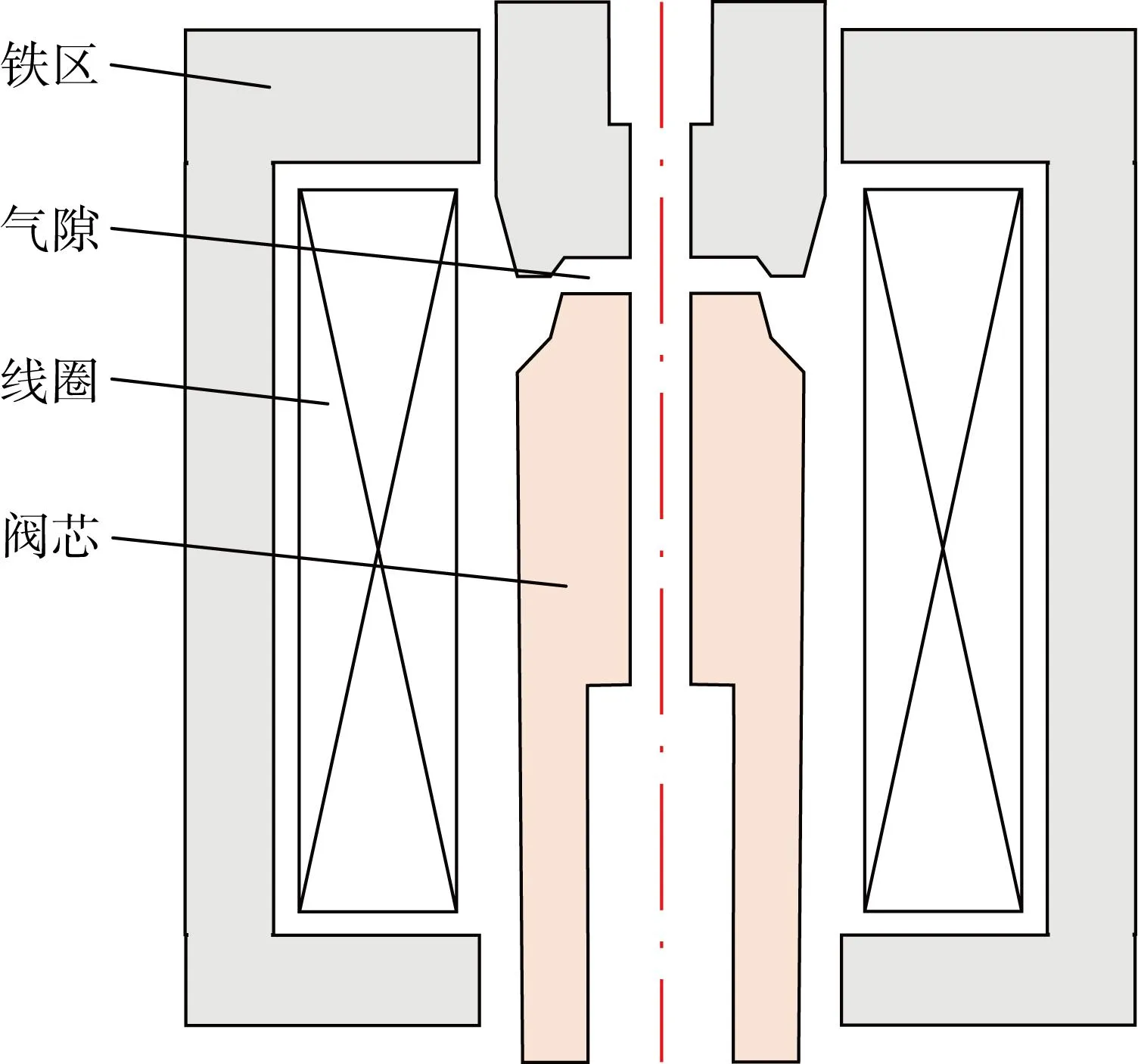
图7 电磁比例阀轴对称几何模型示意图

利用改进的3次磁路-运动耦合模型对电磁比例阀进行快速动态仿真.首先,通过将上、下运动极限处电磁阀的静态电感和阀芯所受磁力的有限元仿真结果代入式(11),确定式(10)中总磁阻3次多项式的4个系数,得到电感和电感梯度表达式,从而确定动态特性方程(3);然后,对方程(3)采用图3(b)中搭建的Simulink系统进行快速求解,得到图8中线圈电流、线圈感应电势、阀芯磁力及位移的计算结果.有限元-运动耦合模型采用三角形网格划分,网格总数为12 284,当衔铁运动时,采用气隙动网格技术求解.通过与有限元-运动耦合模型的计算结果对比,可以发现两者结果曲线较吻合,说明改进的磁路-运动耦合模型可以准确反映有限元仿真结果;此外,改进的磁路-运动耦合模型将有限元仿真所需的626 s缩短仅为1.5 s,大幅提高了电磁比例阀动态特性计算的效率.

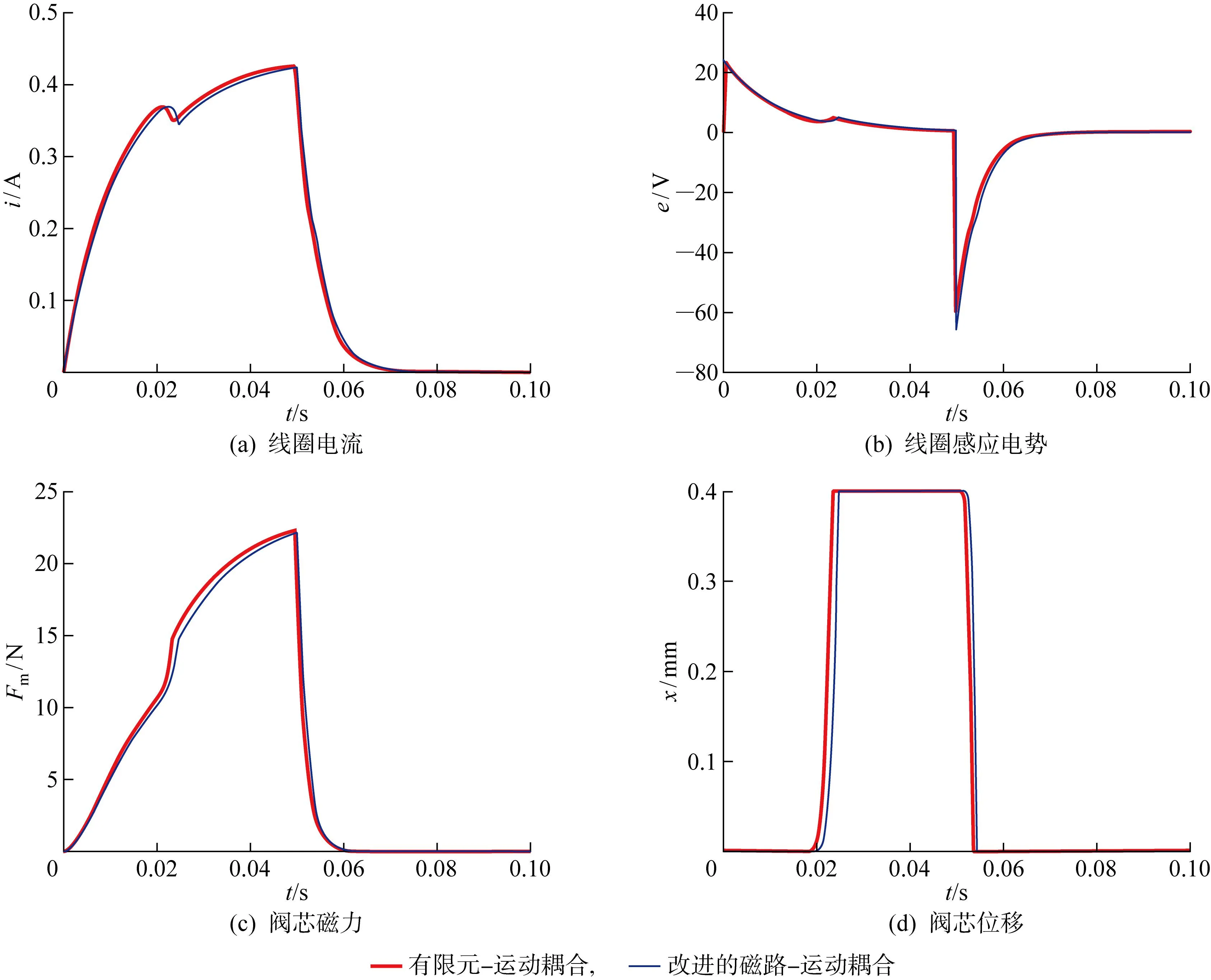
图8 电磁比例阀中改进的磁路-运动耦合模型与有限元-运动耦合模型的结果对比

改进的3次磁路-运动耦合模型与有限元-运动耦合模型并非完全吻合,这主要由于:一方面磁路模型采用3次多项式描述总磁阻,仍然存在一定拟合误差;另一方面改进的3次磁路-运动模型与有限元-运动模型采用了不同的时间离散方案,其中有限元-运动耦合模型中的电磁场模型采用一阶向后Euler法,而改进的3次磁路-运动耦合模型采用Simulink自带的4阶Runge-Kutta法.

5 结语

对未磁饱和的直动式机电运动装置提出一种改进的磁路-运动耦合模型,该模型对非饱和磁路总磁阻采用机构运动位移的3次多项式描述,可更加准确地反映磁力和电感随机构运动位移变化的规律.该模型无需定义铁芯部件和气隙的等效长度和横截面积等,利用机构运动极限处电感和磁力有限元仿真结果或实测值确定总磁阻的3次多项式系数.所得到的改进磁路-运动耦合模型在保证计算精度的同时,实现未磁饱和直动式机电运动装置的秒级快速动态仿真,可有效替代计算耗时的有限元-运动耦合仿真.