提花机拉刀疲劳寿命分析及优化*
2024-01-15瞿书涯
宋 涛,潘 梁,阮 见,瞿书涯,张 波
(南京玻璃纤维研究设计院有限公司,南京 210012)
0 前言
三维机织物[1]具有织造工艺稳定、可设计性强、整体性好、生产成本低等优点,在航空航天领域受到广泛的应用。三维机织物的成型包含送经、开口、引纬、打纬、卷取五大运动[2,3],开口作为机织五大运动的关键一环,采用提花机开口方式,是实现三维机织物的结构变化、自动化织造的重要机构。在生产过程中,提花机拉刀出现周期性的断裂现象,如图1 所示,增加设备使用和维护成本,同时影响生产效率。经动力学分析,拉刀的受载小于材料屈服强度,从而推测拉刀在长时间使用过程中,受周期载荷作用发生应力疲劳失效。

图1 拉刀疲劳失效
通常设备在周期载荷下的疲劳失效主要有应力疲劳和应变疲劳2 种,因疲劳带来的性能损失和使用维护成本提高已越来越受到关注[4]。白传辉[5]等使用多轴疲劳理论分析副车架疲劳破坏问题;黄伟[6]等建立输送带与滚筒接触模型,并分别从厚度和内撑两种方式优化滚筒疲劳寿命;朱茂桃[7]等通过循环系数修正法,采用nCode预测膜片弹簧疲劳寿命。拉刀传动机构一般有曲柄滑块传动和凸轮传动两种,本文主要分析曲柄滑块传动拉刀应力疲劳问题,首先基于Workbench对拉刀在工况下的单周期进行动力学分析,提取拉刀的应力历程,由于拉刀所受应力远小于材料屈服强度,推测发生高周应力疲劳破坏,之后采用nCode基于累计损伤理论[8]分析拉刀疲劳寿命,最后采用等截面积优化方案,提高拉刀疲劳寿命、织物生产效率和设备运行稳定性,降低设备维护使用成本。
1 拉刀动力学分析
1.1 拉刀受力分析
提花机拉刀在一对耦合的曲柄滑块机构驱动下实现拉刀在竖直方向的循环往复运动,如图2 所示。输入端由伺服电机经减速器减速后将动力传递给惯性轮,在稳定运行状态下可以视为匀速运动。在传动末端,拉刀受综丝的拉力,在弹簧作用下,载荷呈线性变化。
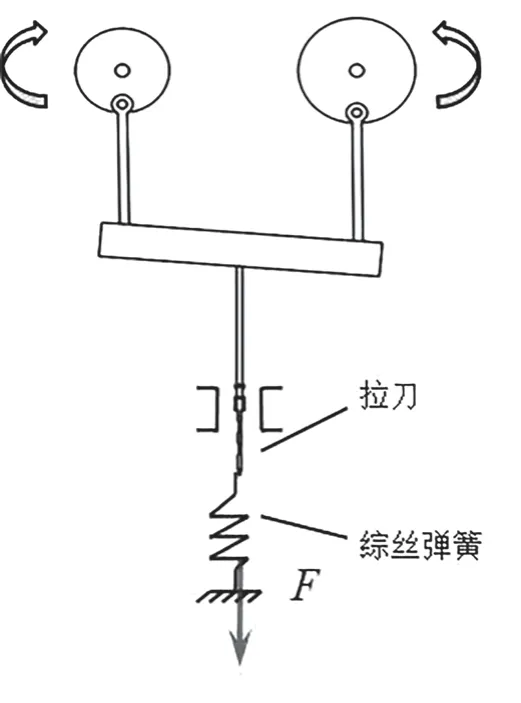
图2 拉刀传动原理图
1.2 基于有限元单周期动力学仿真
以拉刀传动机构为研究对象,建立机构动力学模型,拉刀采用铝合金6061 材料,在曲柄处施加匀速驱动,拉刀受综丝拉力作用,由于断裂失效敏感位置靠近拉刀中间处,故在Workbench中仿真计算拉刀中点的速度、加速度曲线,并提取拉刀应力云图,如图3 和图4 所示。

图3 拉刀中点速度、加速度曲线

图4 拉刀应力云图
由结果可知,拉刀在竖直方向运行速度平稳,沿正弦规律运动。但在初始阶段,拉刀受到冲击载荷作用,加速度发生波动后趋于稳定。在一个运行周期中,拉刀受到最大应力为37.095 MPa,远小于铝合金的屈服强度,可见拉刀并非发生屈服失效,提出猜测可能因疲劳发生失效断裂,需对拉刀作进一步研究。
2 拉刀疲劳寿命分析
2.1 累积损伤模型
为了验证拉刀的疲劳失效形式,通过损伤对拉刀的疲劳做出定量的研究,损伤描述的是从材料初期出现微观上的细纹到后期出现宏观的裂纹扩展过程,拉刀在工况下持续受循环载荷作用,任何一个周期都会对拉刀造成损伤,损伤具有累积效应,疲劳失效可以看作是拉刀的损伤累积到一定值的过程。
目前主要的累积损伤理论主要有线性法[9]和指数法两种,本文采用线性Miner法对拉刀进行疲劳分析。假设拉刀的加载应力顺序依次为σ1、σ2、……σl,对应次数为n1、n2、……nl,加载应力下的寿命为N1、N2、……Nl,那么损伤可以描述为公式(1):
式中:
D——拉刀的损伤;
ni——对应次数;
Ni——加载应力下的寿命。
那么,可以得到拉刀的疲劳寿命,如公式(2)所示:
式中:
L——拉刀的疲劳寿命。
2.2 拉刀疲劳寿命仿真
本文应用有限元法进行疲劳分析,定义铝合金6061 材料的S-N曲线作为疲劳分析的材料属性,根据动力学仿真获取拉刀的载荷-时间历程,计算出载荷激励下的应力响应。根据求取的载荷-时间历程与节点处的激励乘积,经叠加后求得整个应力-应变响应,如公式(3)所示。将上述条件在nCode中计算得结果,如图5 所示。
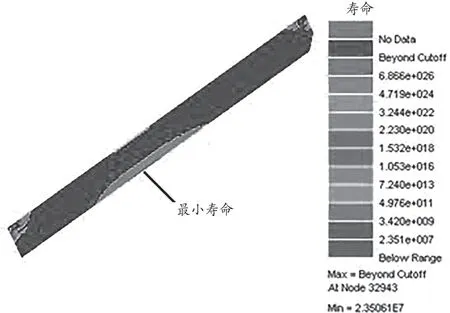
图5 拉刀疲劳寿命结果
式中:
σij——叠加后的应力-应变响应;
l ——载荷数量;
σij,k——激励下节点应力响应;
Fk——载荷-时间历程。
由结果可知,拉刀疲劳危险区域分布于拉刀安装位置和中间下端位置,实际使用时安装位置较可靠,未发生过断裂,而中间下端处为疲劳寿命最低点,循环2.35×107后易在此处发生疲劳破坏,与拉刀实际破坏区域吻合。根据设备的运行时间,寿命约为1.49 年,与班组的拉刀更换时间相符。
3 拉刀结构疲劳寿命优化
3.1 等面积优化方案
为了提高拉刀的疲劳寿命,减少更换零部件造成的宕机损失,降低设备的维护成本,对拉刀结构进行优化设计。根据疲劳寿命结果云图可知,拉刀从下端开始发生疲劳破坏,而两端区域并未受到影响,综合拉刀的外形特点、加工成型工艺以及现有设备的互换性,采用等面积方案对其优化。
拉刀结构可以近似看作为一个薄壁长方形,拉刀端面面积为S,增强寿命最低点处刚度,降低应力集中。以三角形稳定结构强化拉刀寿命薄弱区域,保证整体的面积不变,为优化准则,通过设计高h,避免总体质量增加,如图6 所示。

图6 等面积优化方案
3.2 优化结果
根据等面积优化方案,选取一组高度值,作为拉刀备选结构,施加相同的材料属性、边界条件以及载荷进行仿真计算,如表1 和图7、图8 所示。


表1 等面积优化参数及疲劳寿命

图7 参数h拉刀疲劳寿命
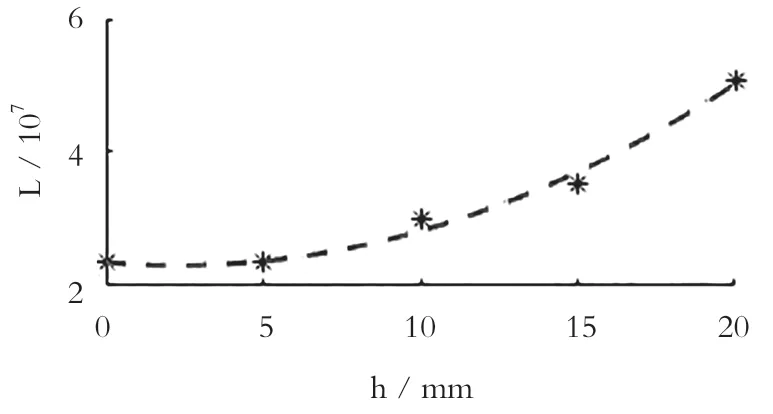
图8 等面积优化疲劳曲线
由图8 可知,随着h增加拉刀疲劳寿命增加幅度呈二次曲线增加,说明等面积优化方案能够有效地提高拉刀的疲劳寿命。然而,参数h受结构尺寸和成型工艺约束并不能无限增加,最大值取20 mm,选取此结果作为最优方案,此时对应的拉刀疲劳寿命为5.092×107次,相较于初始拉刀的寿命增加了一倍。
4 结论
本文针对提花机拉刀在使用过程中出现周期性的断裂现象,经动力学校核后发现拉刀最大应力远小于材料屈服强度,根据拉刀受到的周期性载荷规律,做出拉刀发生疲劳断裂的推测。通过nCode疲劳分析,发现拉刀疲劳破坏部位与断裂部位相吻合,拉刀寿命也与更换时间相符,验证推测有效性。为提高拉刀的使用寿命,提出等面积优化方案,并通过仿真计算不同高度值的疲劳寿命,得到高度值与疲劳寿命呈二次曲线关系的规律。最终选取h=20 mm为优化方案,疲劳寿命相较原先提高一倍。
由结果可知,等面积优化方案能够有效地提高提花机拉刀的疲劳寿命,避免因定期更换拉刀导致设备宕机造成的损失,提高了生产效率和设备运行稳定性,以及降低设备在使用过程中维护的人力与设备成本,为立体织物的稳定生产与高效制备提供了一种理论支撑。
