基于PID 参数的时滞电力系统稳定性研究*
2024-01-15刘晓桂周湘杰蒋逢灵刘小勇
刘晓桂 周湘杰 蒋逢灵 刘小勇
(1.湖南铁路科技职业技术学院铁道供电与电气学院 株洲 412006;2.湖南铁道职业技术学院轨道交通电务技术学院 株洲 412001)
1 引言
随着现代电力工业的飞速发展和互联电网运行规模的不断扩大,电力系统的运行已不能仅依靠局部反馈信号来保持[1]。近年来,基于相量测量单元的广域测量系统的发展与应用为互联电网的协调控制和分布式同步测量带来了新的机遇[2]。广域反馈控制信号虽然能提高系统的动态性能,但其远距离的信号接收与发送存在较明显的时滞现象。大量试验研究表明,时滞现象的存在会降低电力系统的控制性能,使区域电网动态失稳,甚至出现大面积停电现象,所以确保互联电网的安全稳定运行至关重要。众所周知,频率是衡量电能质量的一个重要指标[3]。电力系统稳定运行的要求是确保电网频率始终维持在某个固定值或在某个固定值上下小范围内浮动,而负荷频率控制(Load frequency control,LFC)就是实现这一要求的最常用方法。因此,研究时滞LFC 系统对确保电网的安全稳定运行具有十分重要的价值与意义[4]。
目前,用于时滞电力系统稳定性分析的方法很多,但由于电力系统本身具有时变性与参数不确定性,因此,基于Lyapunov 稳定理论分析法成为最主要的分析方法[5-6]。该方法主要通过构造一个合适的Lyapunov-Krasovskii 泛函,并对泛函进行求导运算,有效处理泛函导数中存在的积分项,从而导出系统渐近稳定的充分条件[7]。它的优点是泛函的解析过程一般可以有效转化为凸优化问题进行求解,缺点是得出的结论具有较大的保守性,有待进一步改善[8]。因此,如何有效降低结论的保守性成为学者们一直努力的方向。文献[9]对时滞电力系统的稳定域进行了分析,由于在Lyapunov-Krasovskii 泛函中引入的自由变量较少,所以运算效率高,但未考虑时滞变化率对电力系统稳定域的影响。文献[10]在构造 Lyapunov-Krasovskii 泛函基础上应用了Wirtinger 积分不等式方法对电力系统稳定域进行分析,在一定层面上改善了结论保守性。文献[11]在应用Wirtinger 积分不等式的基础上引入松散项,推导了含不确定性参数的多时滞电力系统稳定性判据。文献[12]使用PI 控制器研究了在定常时滞与时变时滞情况下含LFC 控制方案的电力系统稳定性。尽管上述文献研究的时滞电力系统稳定性判据的保守性在一定程度上得到了降低,但是构造的泛函都仅考虑引入常实数矩阵,且对泛函导数进行界定时未采用扩展逆凸二次不等式方法,所以使得结论保守性依然明显。
基于上述分析,本文建立了系统矩阵中含PID参数的时滞LFC 系统数学模型。通过构造一个时滞乘积型Lyapunov-Krasovskii 泛函,并应用文献[13]中提出的扩展逆凸二次不等式方法来精确界定泛函导数中的积分项,推导出具有更小保守性的系统稳定新判据。采用典型二阶系统数值算例进行试验仿真,仿真结果表明新判据的有效性。同时,还将新判据应用于系统矩阵中含PID 参数的电力系统LFC系统模型中,分析了系统在不同控制增益参数KP、KI的情况下,KP、KI参数与系统时滞稳定裕度之间的关系。
2 LFC 系统模型建立
在系统的稳定性探讨中,为了分析复杂高阶系统,一般从简单低阶系统着手研究,本文从电力系统中简化的LFC 模型结构入手,分析了系统的稳定性问题,其模型结构如图1 所示[14]。
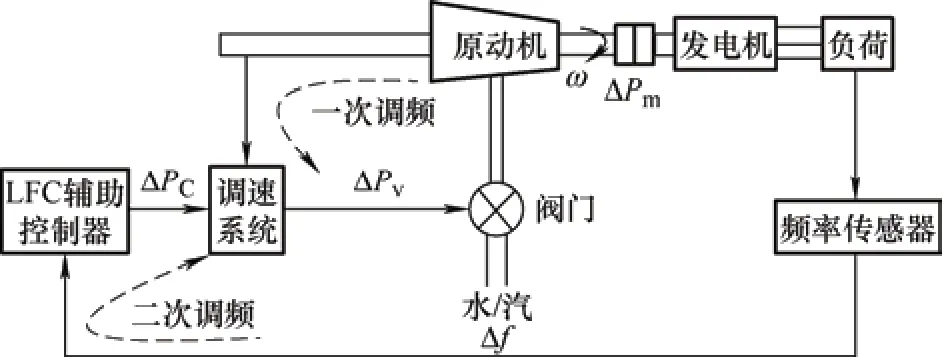
图1 频率调节系统
从图1 可看出,LFC 系统模型结构由五个子模型组成。各模型的简化传递函数式如下所示。
(1) 原动机模型。简化的传递函数式为[15-16]
式中,TT为原动机的惯性时间常数。
(2) 发电机-负荷模型。该模型存在如下关系[14]
式中,ΔPm为发电机机械功率的变化量;ΔPd为负荷端功率的变化量;Δf为频率的变化量;D为发电机的阻尼系数;M为转动惯量。
(3) 辅助模型。目前电力系统中的电能频率控制一般采用PID 控制器来实现,其模型的传递函数为[14]
式中,KP、KI与KD分别为PID 控制器的比例、积分与微分增益;u和ACE 分别为控制输出量和控制误差量;ACE 可定义为[17]
式中,β为偏差因子,可表示为
(4) 调速模型。其模型函数式可表示为
式中,ΔPC是负荷参考值;R是调速器的速度跌落系数;TG为调速器的惯性时间常数。
(5) 时滞模型。时滞主要体现在测量信号的收集与发送中,常采用函数式exp(-s)τ来表示,τ反映了时滞的大小。
综合上述所示,可得出简化的时滞LFC 系统结构框图如图2 所示[17]。
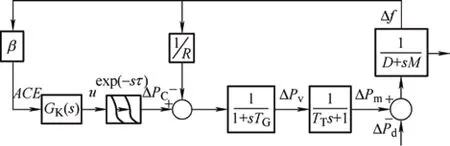
图2 考虑通信延迟的LFC 系统结构框图
定义x(t)和y(t)分别为系统的状态变量和输出变量,由图2 可知
则系统状态空间模型可以表示为
同时,PID 控制器可描述为
假定系统的虚拟变量为
由于CB=0,结合式(8)、(9),可得出如下静态输出反馈控制系统模型
对上述系统进行简化,可得出如下时滞线性系统
假设为系统的平衡点,则存在
则线性时滞系统数学模型为
式中,As与Ads为系统矩阵;τ(t)是时变时滞函数且满足0≤τ(t)≤τ,≤u,φ(t)是系统的初始状态。
3 稳定新判据
3.1 主要引理
为推导出本文新判据,需要用到以下三个引理。其中,Rn×m表示实数域的n×m阶矩阵空间,Rn表示n维向量空间;N为非负整数(即自然数);Sn×n表示n×n的实对称矩阵,上标“T”为矩阵的转置;0 代表合适维度的零矩阵;P>0 表示矩阵P为正定对称;diag{…}表示对角矩阵;Sym{X}=X+XT。
引理1[18]:给定一个n×n实对称正定矩阵R,如果存在标量α、β(α<β)和向量值函数ω,则有以下积分不等式成立
引理2[13]:对于一个n×n实对称正定矩阵R和标量α∈(0,1),如果存在实对称矩阵X1、X2、X3、X4∈Sn×n和任意实矩阵Y1、Y2、Y3、Y4∈Rn×n,满足不等式
则有
引理3[7,13]:给定函数f(s) =a2s2+a1s+a0,其中s∈[0,τ]且α2,α1,α0∈Rn。如果有以下条件成立,则f(s)<0 成立。
(1)f(0) < 0。
(2)f(τ) < 0。
其中,N∈ N,i= 1,2, …, 2N。
3.2 主要结论
本节应用扩展的逆凸二次不等式技术,推导出系统矩阵含PID 参数的时滞LFC 系统稳定新判据。为了简化表示,首先定义如下向量和矩阵。
基于构造的时滞乘积型泛函和逆凸二次不等式方法,得到以下稳定性准则。
定理1:给定两个标量u和τ>0,若存在对称矩阵Q1(∈S4n×4n)>0,Q2(∈S4n×4n)>0,P11∈S5n×5n,P12∈S5n×5n,P21∈S5n×5n,P22∈S5n×5n,Z(∈Sn×n)>0,对称矩阵X1、X2、X3、X4∈S3n×3n和任意矩阵Y1、Y2、Y3、Y4∈R3n×3n,当 式(17)满 足 时 滞 约 束 条 件τ(t) ∈ [ 0,τ],≤u时,则有
则数学模型为式(17)的系统是渐近稳定的。
证明:首先,选取如下Lyapunov-Krasovskii 泛函
式中,P1(t)=P11+τ(t)P12,P2(t) =P21+(τ-τ(t))P22。
注释1:V1(t)中的耦合矩阵包含时变矩阵P1(t)和P2(t)两部分,此时不需要P11、P12、P21和P22均大 于 0 , 只 需 要P11+τ(t)P12>0和P21+[τ-τ(t)]P22>0即可,这增大了矩阵P12和P22的自由度,从而降低了稳定性条件的保守性。当P1(t)>0、P2(t)>0、Q1>0、Q2>0 和Z>0 时,则V(t)>0,即该泛函正定。
然后,对V(t)沿着系统轨迹进行求导运算可得
基于引理1 可得
基于引理2,式(29)右边的逆凸项可以被处理为
其中
综合式(26)~(30)可以得出
式中,ϒ0、ϒ1和ϒ2定义在定理1 中。
因 此,时 滞 在 满 足 约 束 条 件τ(t) ∈[0,τ]和≤u时,若式(24)成立,则有<0成立,从而可以证明数学模型为式(17)的系统是渐近稳定的。
注释2:由于式(23)和式(24)分别是关于α和τ(t)的二次函数,因此需要采用二次函数不等式处理方法将其转化为LMI 形式的稳定性条件。基于引理3 可以得到以下稳定性条件。
定理2:给定两个标量u和τ>0,若存在对称矩阵Q1(Q1∈S4n×4n)>0,Q2(Q2∈S4n×4n)>0,P11∈S5n×5n,P12∈S5n×5n,P21∈S5n×5n,P22∈S5n×5n,Z(Z∈Sn×n)>0,对称矩阵X1,X2,X3,X4∈S3n×3n和任意矩阵Y1,Y2,Y3,Y4∈R3n×3n,当系统满足时滞约束条件τ(t) ∈ [ 0,τ]、≤u且满足式(21)、(22)时,则有
则式(17)是渐近稳定的。
4 数值算例分析
针对文献[19]中提出的PID 控制器的时域性和鲁棒性与两个参数有关的结论,本节深入分析了 PID 参数对电力系统中 LFC 系统稳定性的影响。
4.1 典型二阶系统
本文通过两个常用二阶系统算例来验证新判据的有效性,通过试验仿真证明了新判据在改善系统保守性方面与其他方法相比具有显著优越性。
二阶系统矩阵方程算例一
借助Matlab 中的LMI 工具箱对本文获得的稳定新判据进行试验仿真,试验运算结果及基于相关文献中的稳定性判据获得的结果如表1 所示。其中“—”表示在相应的文献中没有提供这种情况的最大时滞允许上界。
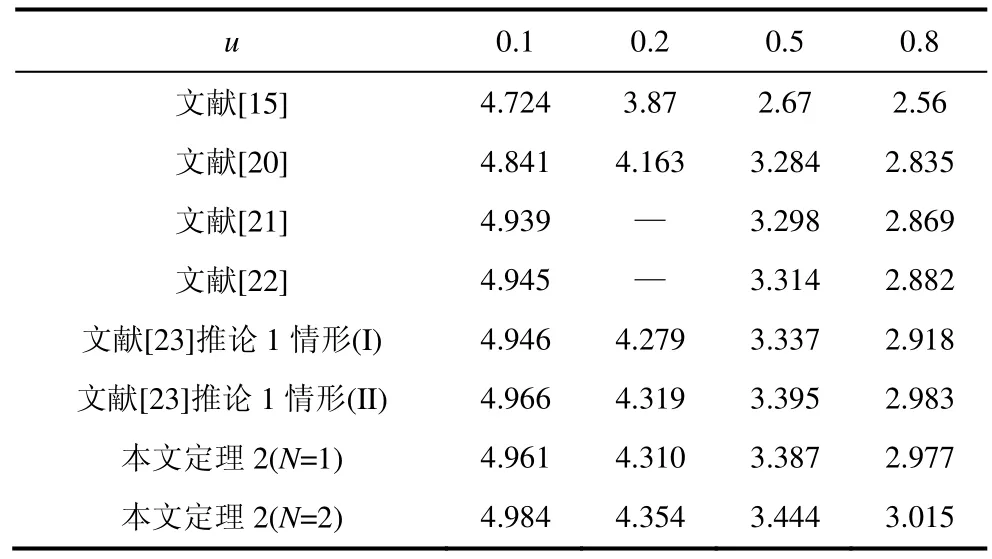
表1 给定不同u 时的系统时滞上界τmax
由表1 可以看出,应用本文推导出的新判据,能让系统的保守性得到很大改善。当u=0.1,N=1时,基于本文定理2 获得的最大时滞允许上界是4.961,由文献[23]中的推论1 情形(I)得到的运算结果是4.946,改善率达到0.303%;而给定u=0.1 时,文献[22]得出的运算结果与文献[21]相比提高了0.006,改善率仅为0.121%。上述对比结果说明,将本文新判据应用于二阶系统矩阵方程算例一中,确实降低了系统的保守性。另外,由图3 还可以进一步看出,由本文定理 2(N=2)得出的系统最大允许时滞上界τmax明显大于文献[23]推论1 情形(II)与文献[22]中的结果,这充分说明了本文构造的时滞乘积型Lyapunov-Krasovskii 泛函以及在界定泛函导数时所应用的扩展逆凸二次不等式方法在降低系统保守性方面与文献[22-23]中的增广型Lyapunov-Krasovskii 以及在界定泛函导数时所应用的其他方法相比具有明显优势。本文构造的时滞乘积型Lyapunov-Krasovskii 泛函考虑了更多系统状态信息,并增大了矩阵P12和P22的自由度,而本文应用的扩展逆凸二次不等式方法在界定泛函导数中出现的积分项时,能使计算值更接近于理论值,从而有效降低了系统的保守性。

图3 通过改变u 获得不同判据下系统的最大允许时滞上界τmax
二阶系统矩阵方程算例二
用同样的试验运算方法,可以得出试验运算结果如表2 所示。

表2 给定不同u 时的系统时滞上界τmax
将本文新判据应用于二阶系统矩阵算例二中进行仿真后发现,本文新判据在算例二中也能减小系统的保守性。
通过对以上二阶系统矩阵方程的算例仿真验证后,可以得出共同结论:本文提出的稳定性准则具有更小的保守性,并且与其他文献中提出的方法相比具有显著的优越性。
4.2 含PID 参数的LFC 系统
本文将新判据应用于系统矩阵中含PID 参数的时滞电力系统稳定性分析当中,目的在于探讨含PID 参数的时滞电力系统稳定性问题,进一步验证本文新判据的有效性。
LFC 系统矩阵方程算例
根据已建立的LFC 系统矩阵方程As、Ads以及相关参数[14](其中,D=1.0、TG=0.10、R=0.05、M=10和TT=0.3),利用Matlab 中的Yalmip 优化工具集成器和SDPT 3.0来求解系统矩阵中含PID参数的时滞电力系统处于定常时滞(u=0)和时变时滞(u=0.5)情况下,PI 控制增益与系统时滞稳定上界之间的关系。运算结果如表3、4 所示。

表3 KP、KI 分别取不同值时的系统时滞上界τmax(u=0)
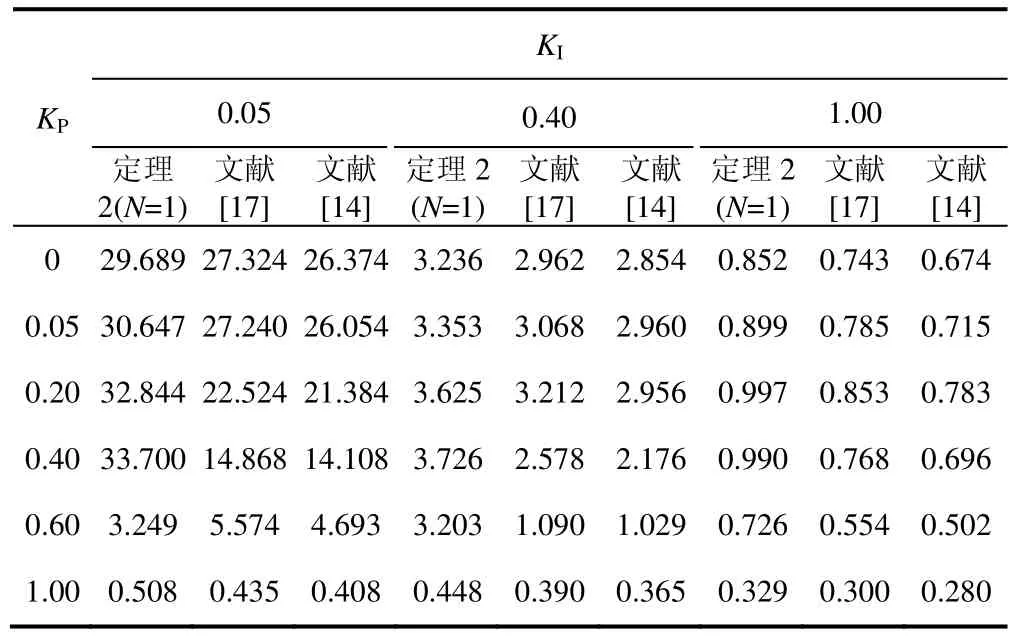
表4 KP、KI 分别取不同值时的系统的时滞上界τmax(u=0.5)
从表3 中可以看出,处于定常时滞(u=0)的情况下,当LFC 系统中的控制增益参数KP、KI分别给定不同值时,应用本文新判据得出的仿真结果明显优于文献[14, 17]中的结果,并且其计算值非常接近于系统最大允许时滞上界理论值,如图4 所示。
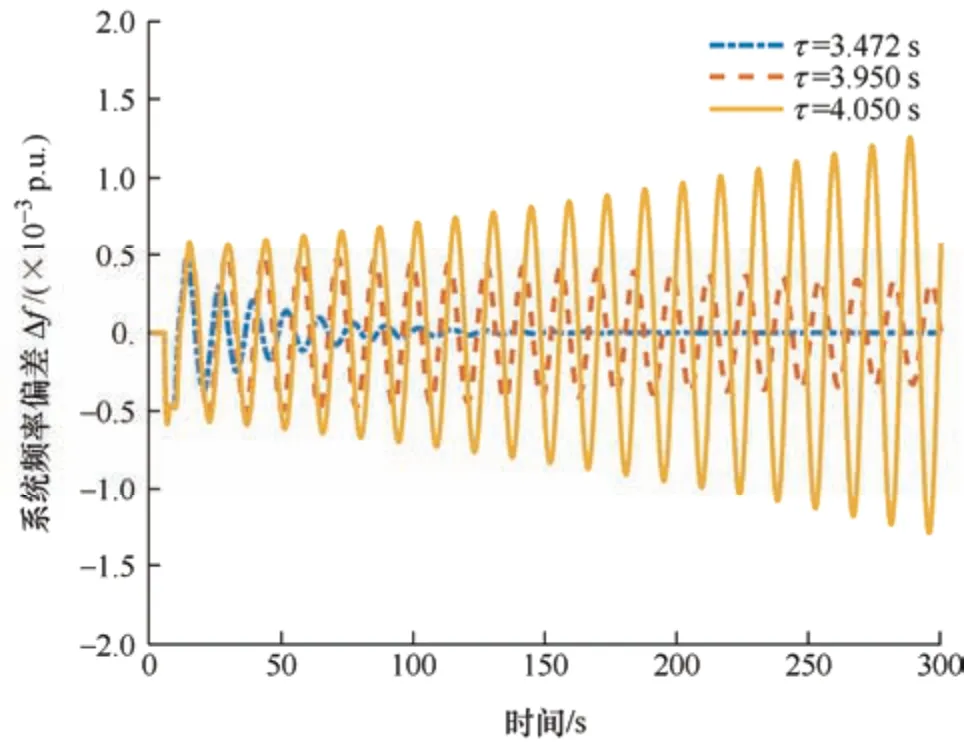
图4 不同时滞下的系统频率偏差(KP=KI=0.4,u=0)
从图4 中可以看出,当τ=3.472 s 时,经过LFC系统的二次调频使系统频率偏差快速收敛到0,这说明通过文献[14]中的稳定判据得到的系统仿真结果非常保守,而当τ=3.950 s 时,系统频率偏差仍然呈收敛趋势,但是保守性得到了极大改善,当τ=4.050 s 时,系统频率偏差呈发散状态,这意味着当KP=KI=0.4,u=0 时,该系统的时滞稳定上界取值范围在3.950~4.050 s。然而,应用本文新判据获得的时滞稳定上界为3.980 s,这说明应用本文新判据获得的最大允许时滞上界非常接近于理论值,同时,也充分证明了本文新判据的正确性。事实上,当τ=3.980 s 时,KP=KI=0.4,u=0 时系统频率偏差如图5 所示。
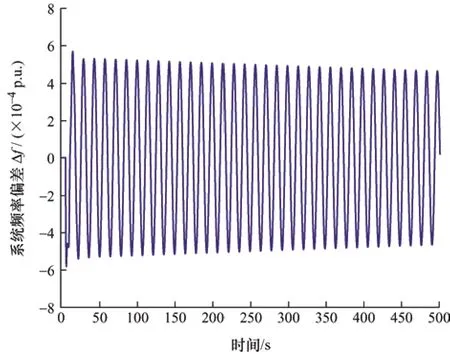
图5 τ=3.980 s 时的系统频率偏差(KP=KI=0.4,u=0)
另外,由表3、4 还可以观察出,增益参数KP、KI的选取会对系统的最大允许时滞上界产生一定影响。当增益参数KI一定时,系统时滞稳定上界随KP的增大呈先增大后减小的趋势;而当增益参数KP一定时,系统的最大允许时滞上界随着KI的增大而减小。
综上所述,将本文定理2 应用在典型二阶系统与含PID 参数的LFC 系统中,都能使系统的保守性得到极大改善,上述试验仿真结果充分验证了这一结论的正确性。
5 结论
为了分析系统矩阵中PID 参数对时滞LFC 系统稳定性的影响,本文以建立的时滞电力系统数学模型为基础, 考虑了构建时滞乘积型Lyapunov-Krasovskii 泛函、扩展的逆凸二次不等式方法,推导出一个时滞电力系统稳定新判据,通过试验仿真得到如下结论。
(1) 通过将新判据应用于两个典型二阶矩阵方程算例与一个LFC 系统矩阵方程算例中,试验仿真结果验证了新判据的正确性以及在改善系统保守性方面与其他工作相比具有显著优势。
(2) 当系统处于定常时滞或时变时滞情况下,改变增益参数KP、KI的取值,系统的时滞稳定裕度与PI 控制增益会呈现一定关系。
