基于CURE 聚类算法的区域滑坡敏感性评价研究

戴俊威，MWAKAPESA Deborah Simon

（1.韶关学院 商学院，广东 韶关 512005；2.江西理工大学 信息工程学院，江西 赣州 341000）

我国黄土面积占全国陆地面积的6.6%，主要占据西北与华北区域，其地貌呈现地势交平、侧壁不明显、滑动面为软塑带，地层为全、厚、大和透水性差而闻名于世. 由于恶劣的地质环境及大量的人类工程活动，黄土地区的黄土滑坡频繁发生且具有多发性、隐蔽性、灾难性和复杂性等特征，严重威胁着当地人民群众的生命财产安全，而滑坡敏感性评价是预测滑坡发生的概率大小，能有效地减少滑坡灾害带来的损失，因此，对黄土滑坡进行敏感性评价具有重大意义.

聚类分析根据研究对象（栅格）的相似特征将其划分成不同的类别，同一类别下的栅格具有一定的相似性，而不同类别栅格之间则差异较大，因其能够发现栅格数据潜在的分布模式，被广泛应用于构建滑坡易发性评价模型. Ding 等采用K 均值（K-means）聚类算法构建三江并流区域的泥石流滑坡危险性评价模型，设置参数为5（很高危险性、高危险性、中等危险性、低危险性和极低危险性），使得聚类结果类型很少，聚类效果差，形成预测精度下降［1］. 由于模糊C 均值聚类（Fuzzy c-means，FCM）算法具有在未知聚类种类的情况下，可结合相关知识探索分类，Wan 等采用FCM 算法来建立滑坡敏感性评价模型，并在Shei-Pei 自然公园等研究区开展了研究［2-3］. 但是FCM 算法仍然具有无确定的聚类结果，需结合相关知识构建分类模型.

综上所述，虽然国内外已有学者采用聚类算法构建滑坡敏感性评价模型，但成果不多，主要问题是模型构建需要设置参数，若模型参数设置不当，会影响聚类效果，导致预测精度下降，笔者研究采用无须设置参数的CURE（Clustering using representatives）聚类算法来建立区域滑坡敏感性评价模型，可以大大提高评价模型的预测精度.

1 研究区域及影响因素

1.1 区域概况

坐落于陕西省延安市的宝塔区是一个3 556 km2的山区，见图1，其地理位置覆盖范围为东经109°14′至110°07′，北纬36°11′至37°02′，海拔高度在800～1 400 m 之间.

图1 陕西延安宝塔区地理概况

延河与汾川河流经该区，丰富的水资源形成了纵横交错的树状地表水系网. 作为黄土高原的一部分，第四系风积黄土在该地占主导地位，黄土覆盖于下伏不平的基岩之上，长期受到密网水系的侵蚀，加之该地区年内降雨较为不均，雨季多集中在6—9月，雨量达到58～117 mm，导致该地区雨季滑坡灾害频发. 由于该地区地质情况复杂，并且作为覆盖黄河中上游的黄土高原的一部分，该地区一直暴露在恶劣的土壤侵蚀中，这些因素都与频繁的滑坡高度相关.

1.2 滑坡因素

山体滑坡的发生与多种因素有关，由于这些因素的选择没有一个固定的标准，因此，在绘制滑坡的敏感性地图时，如何合理地选择这些因素非常重要［4］.根据以往对宝塔区的研究，选择了7 个滑坡条件因子进行建模，它们分别是：坡高、坡角、坡向、曲率、地层岩性、植被覆盖指数（Normalized difference vegetation index，NDVI）和降雨量.

坡高：在高原地区，坡高与滑坡发生的概率高度相关，宝塔区的坡高在20～120 m 之间.

坡角：坡度对物体的滑动和重力作用下的水流有很大影响，进而影响到斜坡的稳定性［5］，宝塔区坡度在25°～55°之间.

坡向：不同坡向光照强度不同，通常朝北方向的阴坡比朝南方向的阳坡更容易发生滑坡灾害.

曲率：曲率将影响地表水势的走向，导致滑坡的发生.

地层岩性：地层岩性是滑坡的物质基础，是衡量暴露在滑坡中的岩石/土壤类型的指标.

NDVI：NDVI 是一个与土壤结构相关的基础生态因子.

降雨量：选择降雨量作为滑坡影响因子是因为频繁的降雨很容易渗透到土壤中，宝塔区多天坑、黄土结构缝隙和风化裂缝，频繁的降雨将在不透水层上形成饱和区域，进而产生孔隙水压力，增加岩石和土块的重量. 以往的研究也记录了雨季滑坡事件发生的频率［6］.

滑坡因素的坡高、坡角、坡向和曲率的地图由数字高程模型生成，分辨率为25 m，比例为1∶10 000，NDVI 和地层岩性地图由增强型专题绘图仪+遥感影像开发，地质地图的比例为1∶50 000，降雨量地图根据气象数据创建，比例为1∶50 000. 在对滑坡敏感性地图建模的过程中将这些滑坡因素称为属性.

2 研究方法

首先用无须指定聚类参数的代表点的聚类法对研究区的样本进行聚类，随后使用K-means 聚类算法将这类聚类结果分成多个滑坡敏感性等级，这样可克服目前使用的聚类方法需指定聚类参数的弊端.

2.1 CURE 聚类方法

CURE 是一种在大型数据集中执行分类任务的聚类算法. 它的工作原理是通过使用一些定义好的代表点（栅格）将大数据集划分为多个聚类子集，并以自下而上的方式创建聚类子集的层次结构. 这意味着该算法要首先指定一个较小规模的数据集，并将数据集中的每个样本作为一个单独的集群. 然后，它从每个聚类中随机选择一小部分分布较好的点作为这些聚类的代表点（Representative points，RePts），并计算每个聚类的RePt 和其他聚类的RePt 之间的距离（欧氏距离）. 然后，该算法将RePts 缩小，并将2 个具有最接近RePts 的子类合并. 缩小和合并的过程将不断重复，直到获得所需的多个子集.

2.2 K-means 聚类方法

K-means 是一种广泛使用的聚类算法，该算法将未标记的数据集作为输入，将数据集划分为k个聚类，并重复该过程，直到k值逐渐趋于稳定. K-means 聚类算法主要完成2 个任务：

（1）通过迭代过程确定k个中心点或质心的最佳值.

（2）将每个数据点分配给它最近的k中心. 靠近特定k中心的那些数据点创建一个集群. 因此，每个集群都有具有一些共性的数据点，并且远离其他集群.

2.3 滑坡密度

滑坡密度L（Landslide density）是用一个子类中每平方千米（km2）的滑坡数量来计算的，用于指定该子类的敏感性等级. 当一个子类中的滑坡数为零时，意味着L也等于零，对于这类情况，将基于该地区的地质地貌特征来确定敏感性等级.

3 区域滑坡敏感性评价与检验

3.1 数据来源

对研究区506 个观测点进行了采样，其中有293 个观测点记录了滑坡信息，依据工程技术人员的经验，选取213 个观测点为不滑坡点，这样就构成了研究所用到的数据测试集. 这些数据集中，存在滑坡现象的样本将被设置为标签为1 的正样本，而不存在滑坡现象的样本将被视作标签为0 的负样本. 对于所有样本都对它们在7月份的坡高、坡角、坡向、曲率、地层岩性、NDVI 和降雨量进行了采样，这样，每个样本都具备7 个属性值，这些属性值将成为后续用于聚类的输入指标.

3.2 聚类分析

采用CURE 聚类算法建立区域滑坡敏感性评价模型主要过程如下：

（1）敏感性单元的划分

借助MAPGIS 软件的二次开发功能，按照规则单元划分的方法，将研究区划分为5 672 922 个栅格，每个网格的尺寸为25 mm×25 mm，其中滑坡观测点的栅格数为24 589. 在CURE 算法中，每个网格被视为带权的节点，其中权值即为上述7 个属性的值，随后对其进行归一化处理，见表1.

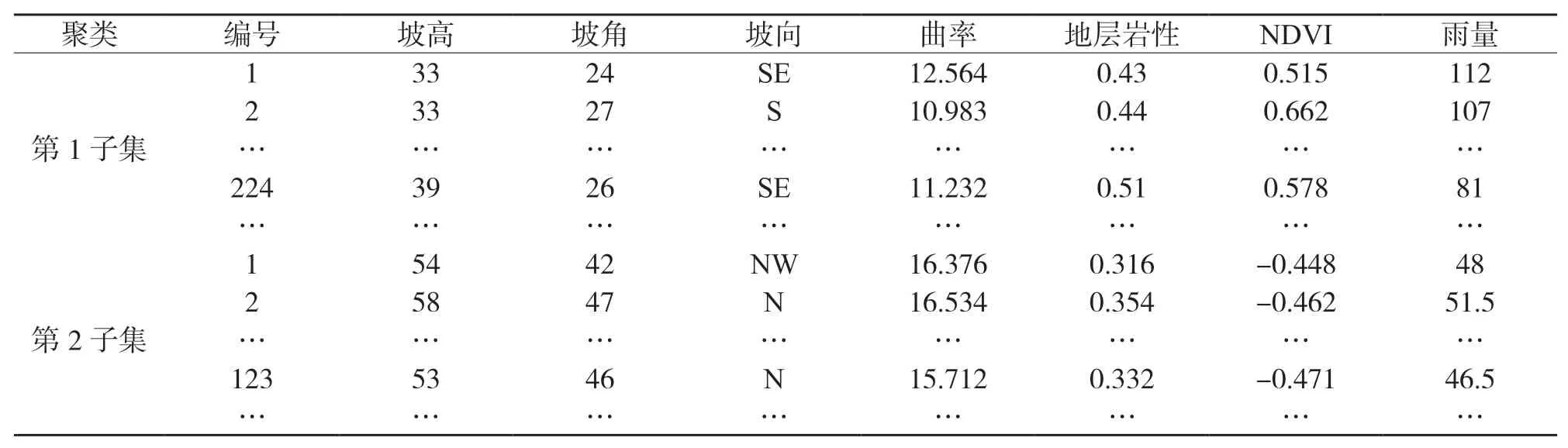
表1 部分聚类子集栅格数据

（2）聚类子集的划分

将每个栅格上所有经归一化后的指标变量（属性）值分别输入到CURE 算法中，得到了483 个具有显著特征的聚集子集，这些子集错综复杂地分布在研究区内，且把研究区内具有相似地质、地貌的斜坡聚集在同一个聚类子集中，见表1.它们无须人工设置各种参数却能对研究区进行较好地聚类，这表明CURE算法在区域滑坡敏感性评价中具有较好的适用性.

3.3 区域滑坡敏感性图的构建

上述的聚类结果只是把具有相同地质地貌的栅格聚集到同一个聚类子集，但是每个聚类子集的敏感性信息不知道. 因此，应用K-means 算法，根据各个子集的L值将各子集划分为4 个敏感性等级（低、中等、高和极高），然后在ArcGIS 10.2 平台上描绘滑坡敏感性地图. 首先，确定每个子集的滑坡数量，计算每个子集的L. 输入每个聚类子集的L至K-means 算法，参数K设置为4（低、中等、高和极高），依据L值，把483 个聚类子集划分为4 个易感等级（图2），划分原则是高滑坡密度意味着高敏感性，而低滑坡密度意味着低敏感性. 如果聚类子集的L值为零，依据其地质、地貌特征，由专家确定其敏感性等级.

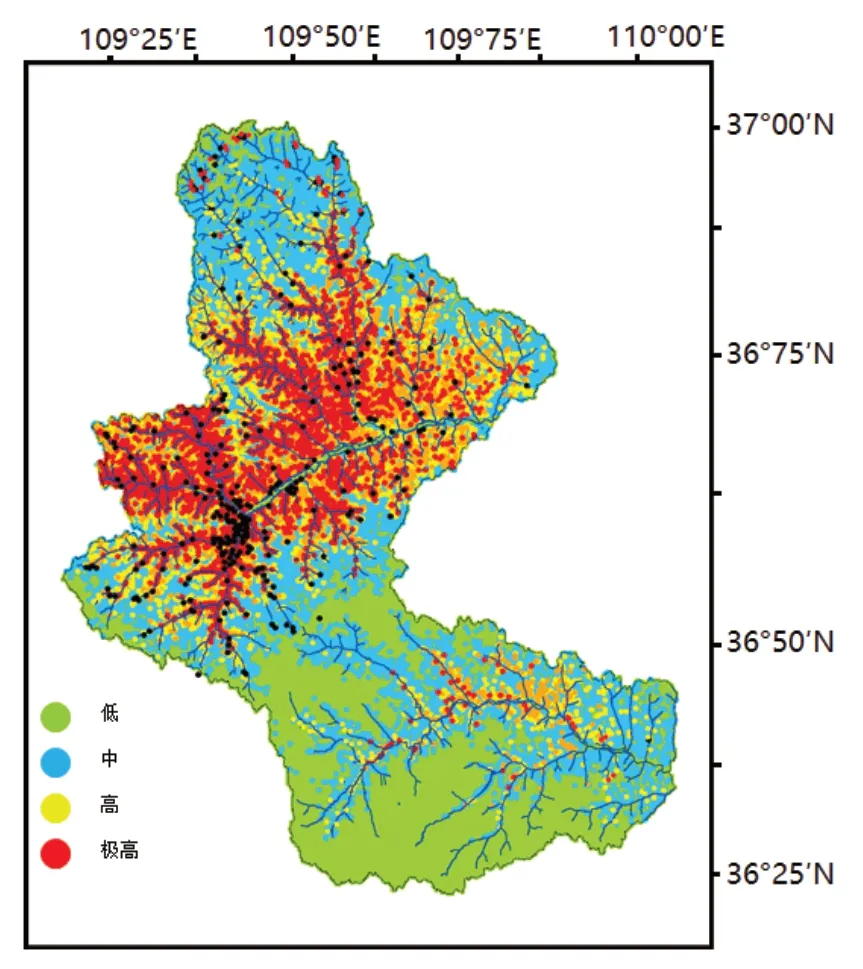
图2 研究区敏感性评价图

经上述分析后，研究区的34%的聚类子集为中等等级，其次是30%的聚类子集为低等等级，19%的聚类子集为高等级和17%的聚类子集为极高等级. 依据实际调查结果，其分布与实际相吻合，见图2.

由图2 可以看出，低敏感性地区主要散落在宝塔区南部；中度敏感性地区主要存在于北部延河流域外的黄土梁峁地带、汾川河南部区域；而极高和高敏感性区主要分布在延河沟谷区内，该区域为延河流域中NDVI 较低的区域，植被少导致水土流失较为严重. 与专家绘制的西安地调中心提供的地质灾害危险区规划图对比，分区结果与其高度吻合.

3.4 评价指标

为评价文中提出方法的有效性，在这项研究中使用了准确度A（Accuracy）作为评价指标，该指标计算如下：

其中，tp为真阳性数，个；tn为真阴性数，个；fp为假阳性数，个；fn为假阴性数，个. 具体而言，tp和fp是分别被正确预测为滑坡和非滑坡的样本数，而tn和fn是分别被错误预测为滑坡和非滑坡的样本数.

3.5 模型检验

准确度是衡量区域滑坡敏感性评价图标准性的指标之一，实验以293 个滑坡和213 个非滑坡观测点为测试样本. 在对比方法上，选择了KPSO（K-means+particle swam optimization）算法，它是K-means 算法和粒子群优化算法的整合，是最近应用于分析滑坡敏感性的有效聚类算法之一，其中以Wan 等提出的方法为代表［7］. 这2 种方法的A值见表2. 从表2 可以看出，CURE 算法的A值比KPSO 算法高17.2%，这一结果体现了CURE 算法比KPSO 算法的聚类能力更优越. 其原因在于，KPSO 算法仍然需要设定参数来确定聚类子集的个数，而对于地质地貌复杂的研究区，聚类子集的参数是很难设置，因此影响了聚类效果，从而造成预测准确度低下，而CURE 算法无须设置参数，采用自上而下的层次聚类方式形成聚类子集，聚类效果较好，从而获得较高的预测准确度.

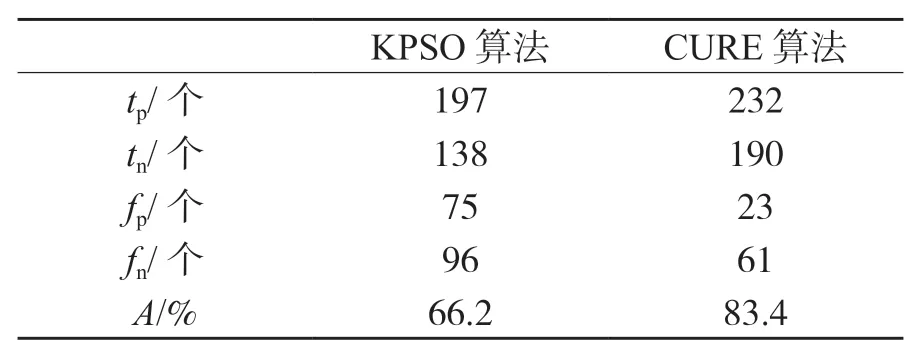
表2 区域滑坡算法A 结果

4 结论

以延安宝塔区为研究区域，进行了基于CURE 聚类算法滑坡敏感性评价，获得了如下结论：

（1）基于宝塔区地形特点，选取了7 个滑坡因素作为模型构建的条件属性，探究了CURE 聚类算法在绘制滑坡敏感性地图中的应用；

（2）选取准确度为评价指标衡量了2 种聚类算法的聚类结果，结果显示，CURE 算法的准确度可达到83.4%，并比KPSO 算法的高17.2%，充分证明了CURE 算法有助于滑坡敏感性预测；

（3）将CURE 聚类算法与滑坡因素相融合能有效构建区域滑坡敏感性评价模型，同时，该方法还可为制定滑坡预防策略及土地规划问题提供思路.