基于ARIMA 模型军工板块波动性研究

李 银，伍晓晴

（韶关学院 数学与统计学院，广东 韶关 512005）

随着人们的收入水平提高，越来越多的人将剩余资金用来投资某些金融产品，比如股票、基金等. 在金融市场背景下，有投资就避免不了风险，股票收盘价会受到各种各样因素的影响，比如，国家的政策、国家的经济情况以及股市的规章制度等. 股票的波动对于广大股票持有者来说非常重要，研究股票的走势非常重要，这会使投资者做出不同的举措来研究与预测［1-2］. 在实现建军100年奋斗目标的背景下，我国需要强大的现代化国防力量，军工投入会不断增加. 与此同时，一些国企有关改革政策的设立和实施，推动了我国军工板块股票热度不断提升. 因此未来几年内，军工板块将会迎来高速、持续、稳定的发展机遇，研究军工板块股票的波动性具有重要的研究意义.

岳朝龙对上海股市收益率进行分析，发现上海股票收益率不仅具有条件异方差，而且具有杠杆效应，因此适合建立GARCH（广义自回归条件异方差）类模型［3］. 萧楠研究发现上海铜期货市场的收益率服从ARMA-GARCH（自回归滑动平均-广义自回归条件）模型，进一步建立TARCH（门限自回归条件异方差）模型和EGARCH（指数条件异方差）模型对收益率的杠杆效应进行检验，发现其并不存在显著的杠杆效应［4］. 张东旭研究上证综合指数收盘价格在不同分布下的ARMA-GARCH 族模型，找到了参数最优、拟合效果最好的模型［5］. 丁文绢对上证A 股50 建立ARIMA 模型和LSTM 模型进行对比，发现通过使用多种深度学习的方法对时间序列同样具有较好的预测精度［6］. 时间序列不仅可以应用于对股票的预测，还可以应用于对其他一些时间序列的变化，例如兰华等比较ARMA 模型和马尔可夫链模型两个模型对光伏电站出力进行预测，进行分析，最后得出时间序列模型ARMA 模型对于预测光伏电站出力预测的精度比传统的马尔可夫链模型的要高［7］. 谭满春等先利用时间序列模型预测交通流的线性部分，再利用人工神经网络预测交通流的非线性部分，两种模型的结合有很好的预测效果［8］.

投资者进行投资时会根据目标产品的投资金额进行调整，以便以最低风险获得最大收益，减少亏损.同时，收益率的预测在单只股票以及资产投资组合中风险的计算起到重要的作用. 因此研究股票时间序列的走势并挖掘其中的特征以及对股票收益率进行预测是不可或缺的. 本文拟对我国股票中证军工板块指数的日收盘价，通过分析主要统计特征，并通过多种检验，建立能预测该板块收盘价波动性的ARIMA 模型，以期对投资者进行下一步决策提供帮助.

1 模型介绍

1.1 ARIMA 模型理论基础

ARIMA（p，d，q）模型是一种自回归整合移动平均模型，是在20 世纪70年代被提出，也被称作Box-Jenkins 模型，专门用于非平稳时间序列分析和预测的方法［9-11］.

参数d是差分阶数，表示将非平稳的时间序列转换为平稳的时间序列时所作差分的次数.

p阶自回归模型（AR 模型）中，要使用时间序列中以前的值，来预测当前值，如当p为3 时，表示使用时间序列中过去3 个时段的值，来预测当前值. 可以表示为，其中Yt表示第t时的观测值，ε表示常数，φi表示自回归参数，Yt-i表示Yt的滞后序列，εt表示随机误差项.

q阶滑动平均模型（MA 模型）中，参数q表示移动平均数的阶数，如当q为3 时，则在预测序列的当前值时，要考虑上3 个时段的平均值的偏差. 表示为，其中bi表示公式的相关系数.

ARIMA 模型是由自回归模型（AR）与滑动平均模型（MA 模型）结合而成，可以表示为Yt=ε+，其中Yt表示第t时的观测值，ε表示常数，φi表示自回归参数，Yt-i表示Yt的滞后序列，bi表示公式的相关系数，εt表示随机误差项.

1.2 确定ARIMA（p，d，q）模型形式

如表1 及图1，模型中的3 个参数确定可以使用的方法有自相关（ACF）和偏自相关（PACF）函数定阶法和赤池信息（AIC）准则，先做出平稳的时间序列的自相关图和偏自相关图，如果自相关图表现出拖尾，且偏自相关图表现出p阶截尾，那么就选择AR（p）模型；如果自相关图表现出q阶截尾，而偏自相关系数表现出拖尾，则选择MA（q）模型；如果自相关图和偏自相关系数均表现出拖尾，则选择ARIMA（p，d，q）模型. 通常情况下，当只用自相关图和偏自相关图难以确定阶数时，再结合AIC 准则来确定模型的阶数. 选择AIC（p，q）最小的时候，此时的p，q为最佳的模型阶数.

图1 模型建立流程图

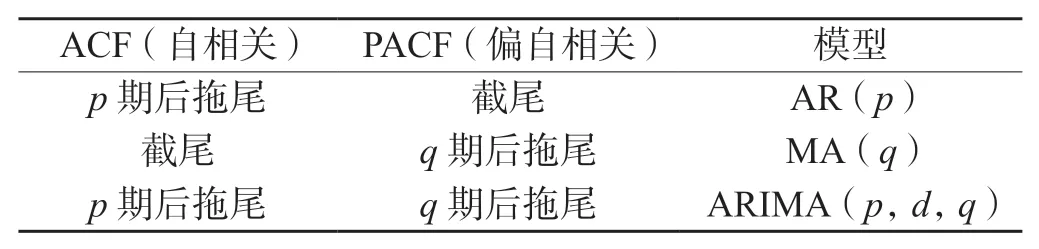
表1 定阶方法

2 实证分析

2.1 数据处理与平稳性检验

由于股票中证军工板块指数可以代表军工板块的整体情况，利用Python 爬取中证军工板块指数（399967）2014年4月4日至2022年12月31日的日收盘价数据作为样本数据，一共为2 020 个. 因为股票的时间序列的走势波动较大，对于大多数时间序列与经济与金融相关的数据都属于非平稳的，时间序列原始数据中可能会包含趋势部分、循环或周期部分以及季节变动部分，需要将不平稳序列变为平稳序列. 利用R 语言画出中证军工板块收盘价的时间序列图，如图2. 可以看出中证军工板块指数的时序图具有明显的走势，则可以初步判断中证军工板块指数是非平稳序列.

图2 中证军工板块指数的时序图

利用R 语言绘制出中证军工板块指数的自相关图和偏自相关图，如图3、图4 所示.

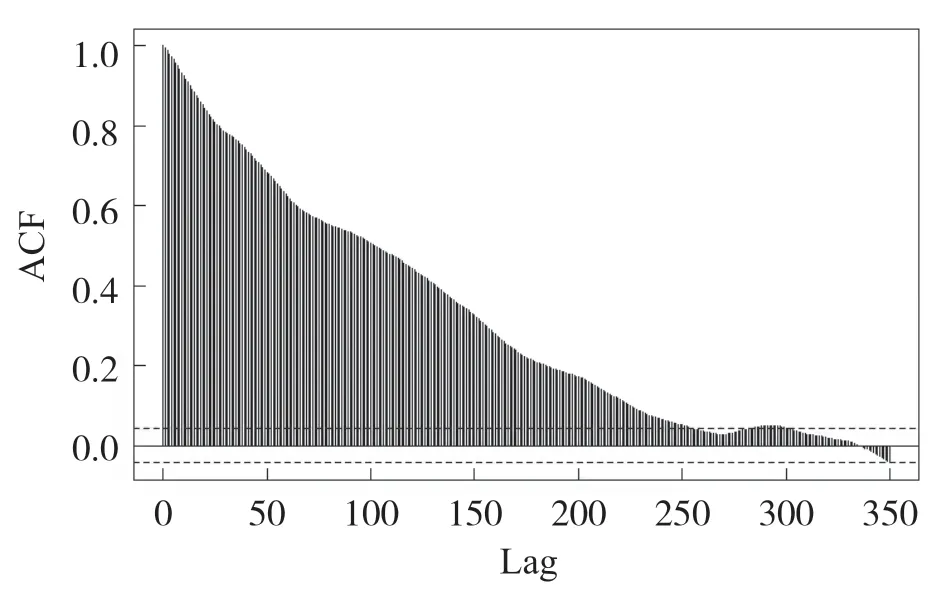
图3 中证军工板块指数的ACF 图

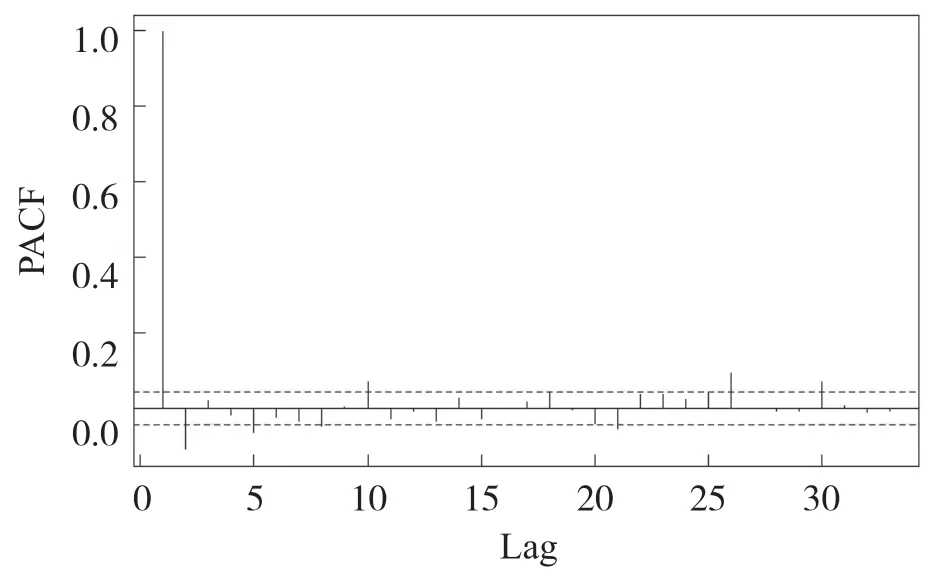
图4 中证军工板块指数的PACF 图

因为中证军工板块指数的自相关函数是慢慢递减，而平稳序列的自相关系数的特点是迅速趋于0，所以该指数具有非平稳性，不能直接建立ARIMA 模型，要先对中证军工板块指数序列做处理，变为平稳的序列，这样才可以用ARIMA（p，d，q）去描述.

因为股票收盘价偏大，为了消除原始时间序列的非平稳性，需要对此取对数，取对数能减少共线性和异方差性出现的概率，然后再做1 阶差分处理，处理后的时序图如图5，可以看出作1 阶对数差分后的中证军工板块指数的收益序列在-0.10 和0.10之间，以0 为基准线上下随机波动，无特别明显的走势和对数差分序列自相关图中是迅速变为0 的，可初步判断该序列为平稳序列.

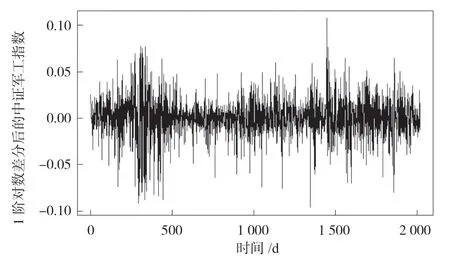
图5 1 阶对数差分后的中证军工板块指数时序图

根据以上分析，中证军工板块收盘价的原始时间序列数据经过1 阶差分处理后得到平稳的时间序列，因此识别选用ARIMA（p，d，q）模型. 因此可以确立模型中的参数d为1 . 接下来需要确立模型中另外2 个参数. 作出AR（p）、MA（q）对数差分的时间序列的自相关图与偏自相关图，见图6 及图7，经观察可初步估计p、q的值. 可知，ACF 图在Lag=2 时开始逐步趋近于0，而PACF 图是截尾的，因此模型AR 的阶数p可以判定为1，2，3，模型MA 的q则为0.

图6 中证军工板块指数1 阶对数差分ACF 图

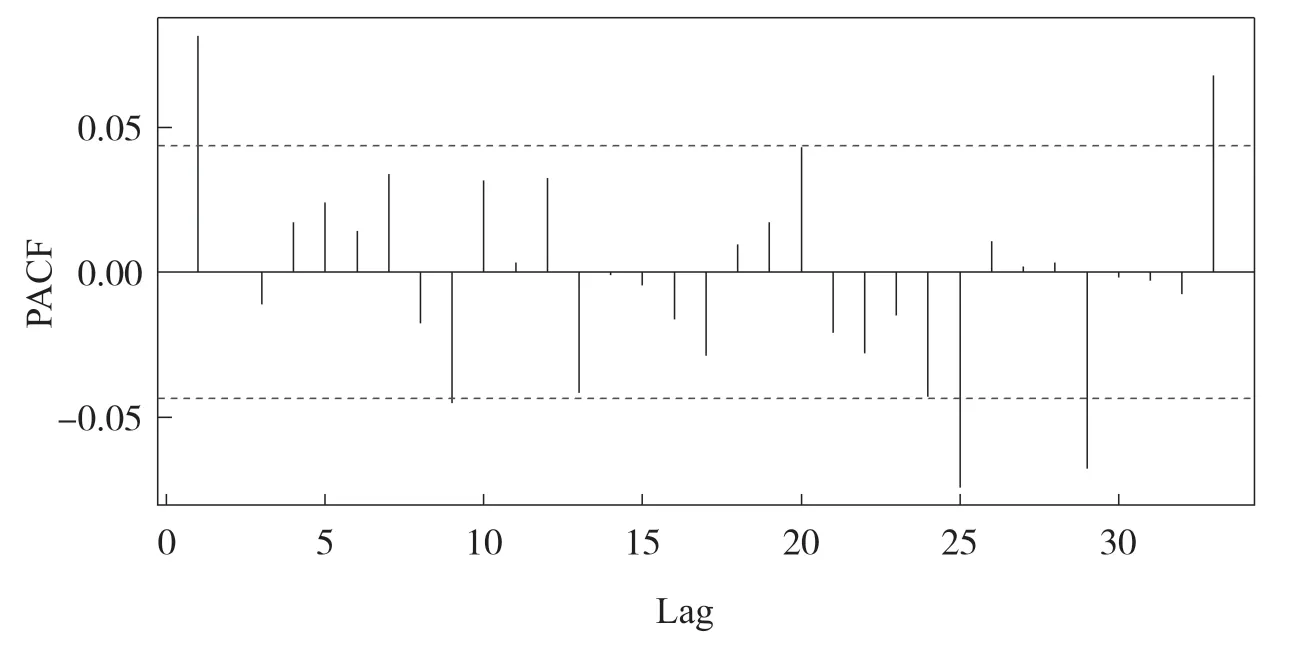
图7 中证军工板块指数1 阶对数差分PACF 图

从理论上对中证军工板块指数和1 阶对数差分序列进行ADF（单位根检验）的平稳性检验，单位根检验是检验序列是否平稳的主要方法. 本文利用软件EViews 8.0 对序列进行平稳性检验，检验结果如表2.

表2 ADF 检验结果

如表2 所示，在1%的显著性水平下，原序列P值为0.059 6＞0.05，为非平稳序列. 进一步检验中证军工板块指数对数差分后的序列是否通过平稳性检验，对数差分后的序列P值＜0.05，日对数收益率序列通过了检验，对原假设表示拒绝，即对数差分后的序列已经是平稳序列，至此，完成了原始数据的平稳性处理. 因此可以确定序列是1 阶单整序列，则ARIMA（p，d，q）模型中d=1.

2.2 模型参数选择（模型定阶）（AIC 准则）

利用EViews 分别建立3 个模型AR（3）、AR（2）和AR（1），同时比较3 个模型的赤池信息，如表3 所示. 由表3 可知，AR（2）模型的AIC 值是-4.826 700，是最小的，因此建立ARIMA（2，1，0）模型对应的表达式为：lnat=1.078 206×lnat-1-0.083 336×lnat-2+9.262 814.

表3 3 个模型的信息

2.3 模型检验

对建立的模型进行拟合优度和显著性检验，发现模型的预测收益率与实际的收益率几乎重合，ARIMA（2，1，0）的判定系数R2为0.992 254，拟合优度很好.

2.4 残差序列相关性检验

还需要对1 阶滞后进行残差序列相关性检验，由于1 阶对应的LM 检验统计量Obs*R-squared 的P值为0.910 2，表示在5%的显著性水平下，接受原假设，说明建立的ARIMA（2，1，0）的残差无自相关性，即没有遗落变量，所以滞后阶数选取是合理的.

2.5 异方差检验

模型的参数已经估计后，对已经建立的ARIMA（2，1，0）模型的随机残差序列进行白噪声检验. 结果表明P值都大于0.05，表明全部的Q值小于检验水平为0.05 的卡方临界值，拒绝原假设，随机误差项是一个白噪声序列，异方差效应不显著，也就是说建立的模型的残差序列中几乎没有包含有用信息，则不需要继续对残差建立GARCH 模型，该模型的建立是合理的.

2.6 预测分析

由于建立的时间序列模型拟合精度很高，则本文利用上述已经建立的ARIMA（2，1，0）模型对股票序列对未来3 天中证军工板块指数收盘价进行预测，在R 中调用forecast 函数，预测2023年1月3日至2023年1月5日3 天的收盘价. 预测的结果如表4，结果表明，建立的ARIMA（2，1，0）模型较为准确，对该只股票日收盘价的预测有很好的现实意义. 代码如下：

表4 预测的收盘价以及相对误差

3 结束语

笔者对我国股票中证军工板块指数的日收盘价格中所获取的数据进行处理，依次经过平稳性检验、参数确定、模型建立、异方差检验，再利用ARIMA 模型对中证军工板块指数的日收盘价建立模型，并预测未来3 天的收盘价，对金融市场中的股票的基本特征有了更进一步的了解. 研究发现，时间序列模型能很好地解决了一些非平稳股票时间序列的模型建立的问题，且模型非常简单，容易操作，所涉及的只有内生变量股票的收盘价，结合Eviews 和R 语言可以将时间序列模型应用到其他金融时间序列，尤其在金融和股票领域有重要的理论意义，预测值的准确性对投资者和决策者起着非常重要的作用.

但是由于股票的时间序列价格变动较大，因此该类模型适合短期预测，对于长期预测的结果会与真实值有较大的误差［9-11］. 因此还有待进一步的研究.