基于NX的弧面分度凸轮参数化实体建模与仿真加工研究

黄 涛,赵世田,陆子恒, 曾 勇,吕守宝

(盐城工学院机械工程学院,江苏 盐城 224051)

弧面分度凸轮机构属于间歇运动机构中的一种,用于主动件轴线与从动件轴线相互垂直交错的间歇分度步进传动。其主动凸轮由圆弧回转基体和突脊状的凸轮轮廓组成,从动转盘上装有若干个沿转盘圆周均匀分布的转子。该机构具有定位准确、结构简单、质量轻、刚性好、分度精度高等特点,并且能通过改变中心距调整滚子与凸轮槽之间的间隙减小或补偿磨损。在机构转位期间,从动转盘的运动规律可依据实际转速与负荷要求进行设计。因此该机构非常适用于高速、重载、高精度的场合,目前主要作为加工中心自动换刀系统、数控分度转台等需要周期性间歇转位的自动化机械核心传动部件。

弧面分度凸轮在实际生产应用中按滚子形状进行分类,其中圆柱滚子弧面分度凸轮应用最为广泛。付正飞等[1]在Pro/E软件中实现了圆柱滚子弧面分度凸轮的设计建模与仿真加工。朱洋[2]根据两重包络原理对圆柱滚子弧面分度凸轮进行侧铣加工刀具路径轨迹规划与仿真。胡东方等[3]提出了基于刀位补偿法的圆柱滚子弧面分度凸轮非等径侧铣加工刀位优化方法。张文光等[4]利用SolidWorks软件缩短了弧面分度凸轮建模时间。目前凸轮的相关设计建模理论研究已经成熟,但针对其运动动力学和加工理论的研究有待完善,而且我国多轴加工中心配套的高精度自动换刀系统大多需要进口,面对国外技术封锁,国内需加强此方面的研究。

本文基于MATLAB编程计算软件与NX 12.0软件建立圆柱滚子弧面分度凸轮廓面方程与三维模型,利用NX软件中计算机辅助制造(computer aided manufacturing,CAM)模块进行数控编程,最后通过VERICUT软件进行五轴数控仿真加工。

1 弧面分度凸轮廓面方程

1.1 弧面分度凸轮机构坐标系统的建立

基于圆柱滚子弧面分度凸轮机构建立4个坐标系(图1),每个坐标系均采用右手定则,定义如下:

图1 圆柱滚子弧面分度凸轮机构坐标系统

2)坐标系{o0x0y0z0}为固定坐标系,原点o0位于从动转盘中心,x0方向朝向转盘对称面与凸轮轴线的交点,z0与转盘轴线重合,方向从里向外,根据右手定则,y0由x0和z0确定方向,角速度ω2的转向为逆时针。

4)坐标系{o2x2y2z2}是运动坐标系(固连于转盘),原点o2与原点o0重合,x2沿着转盘径向线与转子自转轴线重合,o0x0与o2x2的夹角φ为滚子的位置角,沿着z0轴正方向看,从o2x2以逆时针为正方向开始测量。

1.2 共轭接触方程式的建立

根据共轭接触曲面原理,圆柱滚子与弧面分度凸轮廓面的共轭接触点需要满足3个条件:1)在共轭接触位置,两曲面上对应的共轭接触点必须重合。2)两曲面的相对速度在共轭接触点处必须与其公法线垂直。3)在共轭接触点处,两曲面必须相切且无涉,亦无曲率干涉。

由上述条件2)可得,在共轭接触点处的相对运动速度始终垂直于公法线[5],从而确定共轭方程式:

(1)

式中:p为凸轮分度期轮廓线的旋向,p=+1为左旋,p=-1为右旋;C为中心距;ω1、ω2分别为凸轮角速度与转盘角速度;ψ为共轭接触角;r为分度转盘节圆半径。

1.3 基于齐次坐标变换的弧面分度凸轮廓面方程

在不同的坐标系中,圆柱滚子弧面分度凸轮廓面上的共轭接触点1P与滚子面上的共轭接触点2P之间的矢量变换关系,可以根据共轭接触理论通过空间运动的齐次坐标变换计算得到[6]。通常为了方便公式推导,默认滚子不作自转运动。

由各坐标定义可知滚子面上的共轭接触点位于坐标系{o2x2y2z2}中,则滚子面上的共轭接触点2P的齐次坐标表示为:

(2)

式中:Rr为滚子半径。

故2P点从坐标系{o2x2y2z2}齐次变换到坐标系{o1x1y1z1}中的过程如下:

(3)

从坐标系{o2x2y2z2}变换到坐标系{o0x0y0z0}的齐次变换矩阵:

(4)

(5)

(6)

则:

(7)

展开式(7)得到圆柱滚子弧面分度凸轮廓面方程通用表达式:

(8)

式中:(x1,y1,z1)为圆柱滚子弧面分度凸轮廓面坐标,(x2,y2,z2)为滚子面上的共轭接触点坐标。

2 弧面分度凸轮参数化三维模型

针对较为复杂的弧面分度凸轮曲面参数化建模,主要有等距曲面法、直接建模法、点—线—面法[7]这3种方法,其中等距曲面法和直接建模法设计步骤繁琐且得到的凸轮廓面与理论凸轮廓面之间存在一定差异,而点—线—面法设计方便,建模效率高,故本文选用此方法,利用MATLAB软件编程计算曲面坐标点数据,并导入NX 12.0软件建立圆柱滚子弧面分度凸轮三维实体模型。凸轮机构轮廓线旋向为左旋,轮廓线头数为单头,并采用修正正弦加速度的运动规律,基本参数见表1。

表1 弧面分度凸轮机构基本参数

2.1 采集弧面分度凸轮廓面数据点

根据式(8),在MATLAB软件中分别对1L、2R、2L、3R段凸轮廓面坐标点以及停歇期凸轮廓面坐标点进行编程计算[8],图2所示为1L段凸轮廓面坐标点。

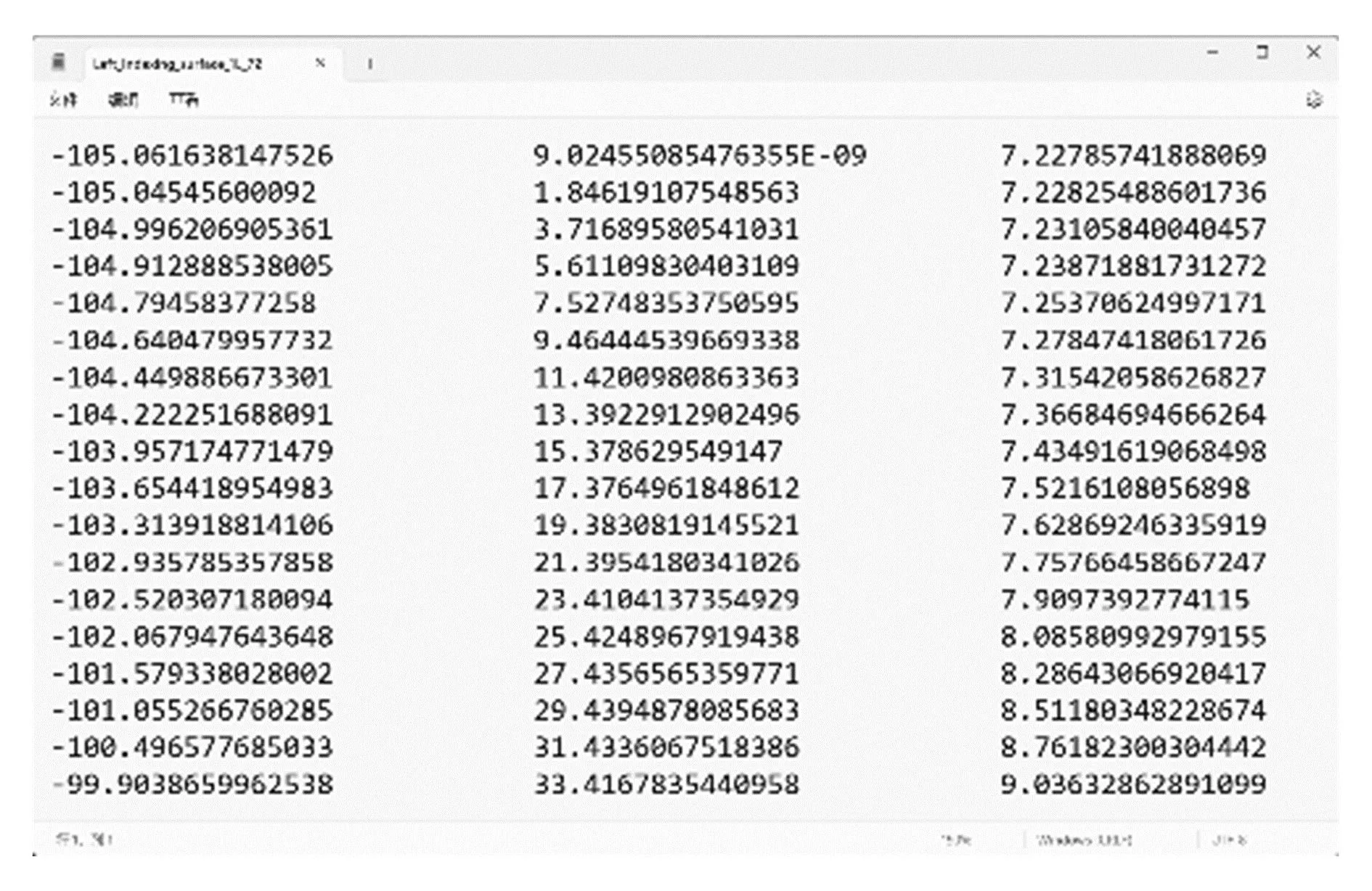
图2 1L段凸轮廓面坐标点

2.2 弧面分度凸轮三维实体建模

在NX 12.0软件中,首先将计算出的凸轮廓面坐标点导入,得到凸轮的轮廓线(图3a),拟合成凸轮廓面(图3b),然后通过“缝合”命令实体化(图3c),建立凸轮基体,合并得到圆柱滚子弧面分度凸轮参数化三维实体模型(图3d)。

图3 弧面分度凸轮三维建模

3 弧面分度凸轮五轴数控加工工艺及编程

3.1 弧面分度凸轮的加工设备及装夹定位

弧面分度凸轮的加工设备一般选择2(移动轴)+2(旋转轴)或者3(移动轴)+2(旋转轴)类型的数控机床,本文选择3+2类型的五轴数控机床,型号为Hermie_c42,采用双转台,机床主要信息见表2。

表2 Hermie_c42五轴加工机床主要信息

毛坯选取车削好的圆柱弧面毛坯,毛坯直径为凸轮定位环外圆直径,毛坯宽度与凸轮实际宽度一致。利用T型螺栓将专用心轴夹具固定到机床的工作台之上,再配合螺母将凸轮毛坯固定在夹具的中心轴上,如图4所示。

图4 弧面分度凸轮一次装夹

3.2 弧面分度凸轮加工方法理论分析

目前对于弧面分度凸轮加工,主要有等价加工法(范成法)和非等价加工法两种方法。等价加工法要求专用的凸轮加工机床以及刀具必须是与滚子直径相同的定制刀具,因此刀具与滚子的曲面是一致的,凸轮的加工精度较高,但也限制了刀具的选用,无法适应不同类型的滚子和不同几何参数的弧面分度凸轮。另一方面,等价加工法存在同时顺/逆铣情况,导致零件表面加工质量较差,而且专用定制刀具磨损后会出现无法补偿的加工误差。非等价加工法选用直径小于滚子直径的标准刀具,相比之下,非等价加工法具有刀具选用更灵活、加工效率更高等优点。目前非等价加工法主要有两重包络法、刀位补偿法和自由曲面法[9]。其中自由曲面法是以等距曲面理论为基础,刀具中心会一直处于凸轮工作廓面的等距曲面上,刀轴会按照从动转盘的轨迹路线转动,以此来补偿因刀具直径变小所造成的摆动中心偏移量。此方法克服了等价加工法的缺点,可以完成凸轮工作廓面单侧面加工,凸轮表面加工铣削精度较高。CAM(计算机辅助制造)可变轮廓铣模块中“曲面区域”和“外形轮廓铣”驱动方法的原理也是基于自由曲面法,故本文采用自由曲面法。

3.3 弧面分度凸轮五轴数控加工编程

基于CAM强大的数控加工编程功能,对圆柱滚子弧面分度凸轮进行数控加工编程,加工工艺见表3。

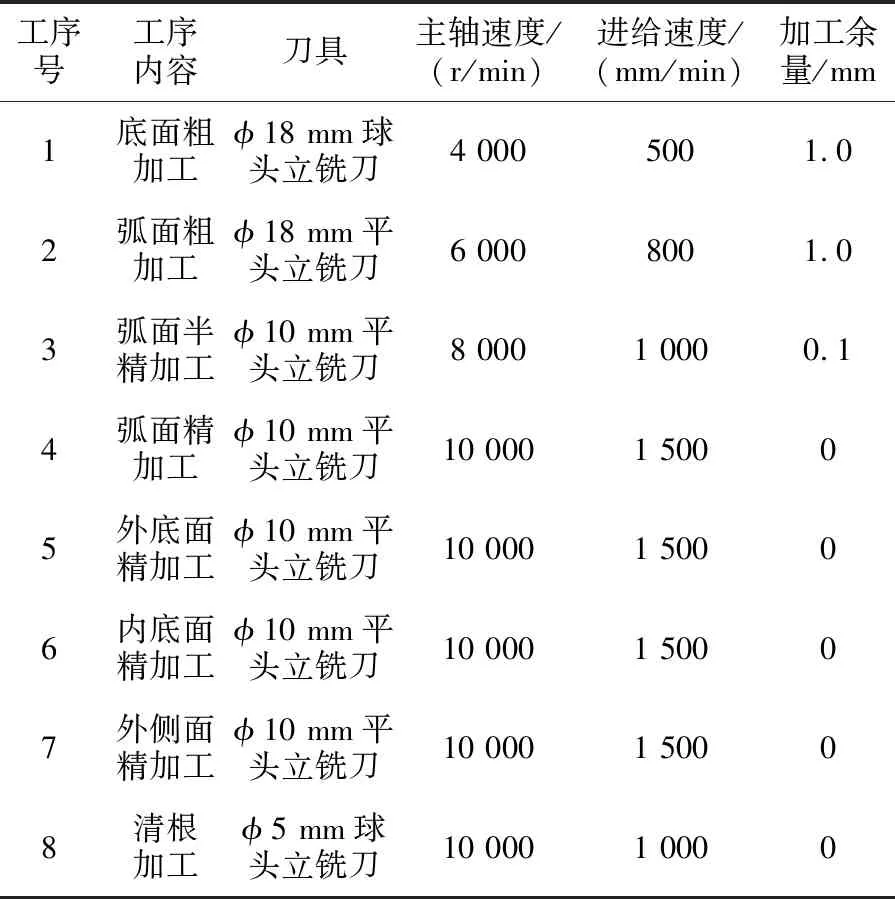
表3 弧面分度凸轮加工工艺表

具体操作过程如下:粗加工分两步进行,第一步对凸轮进行粗加工,选用CAM可变轮廓铣模块中“曲面区域”驱动方法,按图4所示设置好工件与毛坯,创建φ18 mm双刃球头立铣刀,选择凸轮底面为切削区域,将刀轴方向设置为远离直线(凸轮径向),生成的刀具路径如图5(a)所示。通过CAM导轨可视化3D动态模拟发现一次粗加工后凸轮工作廓面部分仍留有较大毛坯余量,因此第二步需要对其进行二次粗加工。考虑到凸轮工作廓面为不可展直纹面,为了提高加工精度,需要进行侧铣加工,所以选用“外形轮廓铣”驱动方法,刀具改为φ18 mm双刃平底立铣刀。将凸轮底面设置为指定底面,以凸轮弧面为指定壁,进刀矢量设定为+Z,生成如图5(b)所示的刀具路径。

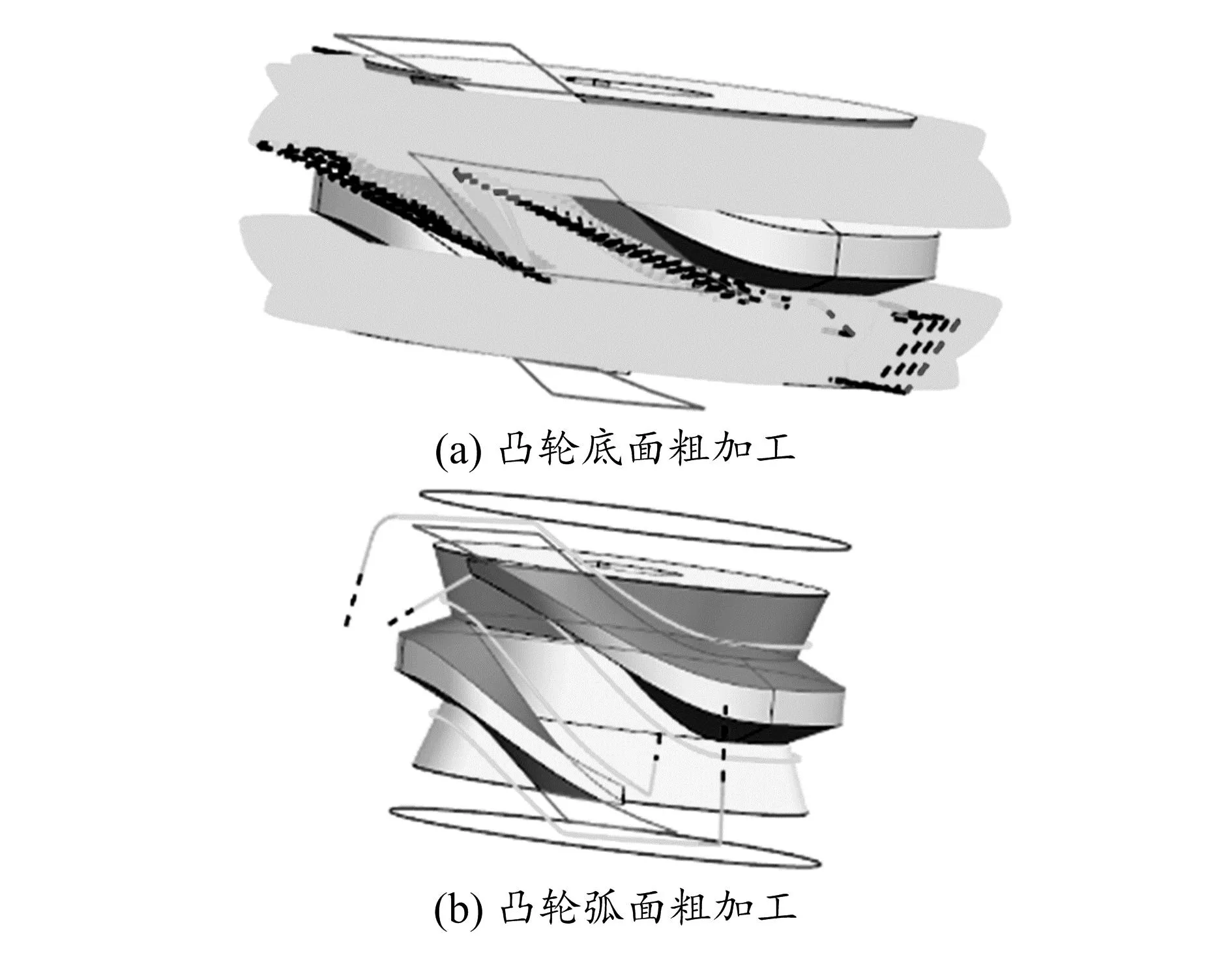
图5 弧面分度凸轮粗加工

分度期凸轮廓面加工是凸轮加工最核心的部分,需要进行半精加工与精加工,操作与上文二次粗加工一致,只需将加工刀具替换为φ10 mm的双刃平底立铣刀,同时在切削参数中设置多条侧面刀路数,以及在半精加工与精加工中将余量参数分别设置为0.1和0,生成刀具路径如图6(a)所示。

图6 弧面分度凸轮精加工

精加工凸轮内外底面时,凸轮内外底面对应的加工策略是不同的,所以需要分开加工。选用可变轮廓铣模块中“流线”驱动方法加工凸轮外底面,刀轴方向设定为垂直于部件,投影矢量设定为垂直于驱动体,检查体指定为凸轮外侧弧面,以防止刀具对弧面过切。因为凸轮内底面是个规则的圆柱面,所以加工策略选用“曲面区域”驱动方法,刀轴方向和投影矢量与精加工外底面时一致,检查体为凸轮内侧弧面,刀具不变,余量改为0,最终生成刀具路径如图6(b)、图6(c)所示。对于凸轮外侧面的精加工,选用“外形轮廓铣”驱动方法进行侧铣加工,指定底面为凸轮上/下弧面,指定壁为凸轮外侧表面,进刀矢量设定为+Z,其余参数与上述一致,刀具路径轨迹如图6(d)所示。

在上述凸轮精加工过程中,因为加工刀具直径大导致凸轮底面与凸轮弧面接触位置留有毛坯余量,所以需要对凸轮进行清根加工,首先将凸轮底面与凸轮弧面的接触线分别在两个面上偏置3 mm,然后驱动方法选择多轴轮廓铣模块中的“Variable Guiding Curves”,以偏置曲线为引导线,刀轴方向为凸轮径向,刀具选择 5 mm的双刃球头立铣刀。余量改为0,最终生成的清根加工刀具路径如图7所示。

图7 弧面分度凸轮刀具路径

完成弧面分度凸轮加工编程后,按照表2机床结构信息,建立五轴数控加工机床后置处理器,按照工序,依次输出各个数控加工编程,并保存为NC文件。

4 基于VERICUT弧面分度凸轮虚拟仿真加工与分析

4.1 虚拟数控机床加工仿真环境构建

首先,根据Hermie_c42五轴数控加工机床各轴实际相关参数以及相互之间的运动关系,在NX 12.0软件中建立机床组件模型并导出为STL文件,然后导入VERICUT软件中,构建Hermie_c42五轴机床加工仿真环境,结构模型如图8所示。最后依据表3中所列的刀具尺寸,在VERICUT中创建刀具并存为Hermie_c42刀具库文件。

图8 Hermie_c42机床结构模型

4.2 弧面分度凸轮加工仿真与结果分析

在VERICUT中,新建圆柱滚子弧面分度凸轮仿真加工项目,将上述机床模型、控制系统文件、刀具库文件以及夹具依次导入项目树中,并将夹具安装到机床工作台中心位置。然后导入毛坯和零件,在毛坯中心位置建立加工坐标系G54。最后按照工序将数控NC文件载入。仿真机床与凸轮实际仿真加工如图9所示。

图9 弧面分度凸轮VERICUT实际仿真加工

数控机床仿真加工完成后,设置残余高度允差为0.05 mm,将加工后零件与设计零件进行对比(图10),对比结果见表4,没有发生过切。图10中凸轮工作弧面与分度期外侧面部分加工残余稍高,零件整体残余高度符合要求。之所以分度期工作弧面与外侧面部位留有稍大的残余高度,是因为弧面的不可展直纹面导致侧铣加工中刀具无法与切削曲面完全贴合,从而产生原理性误差。

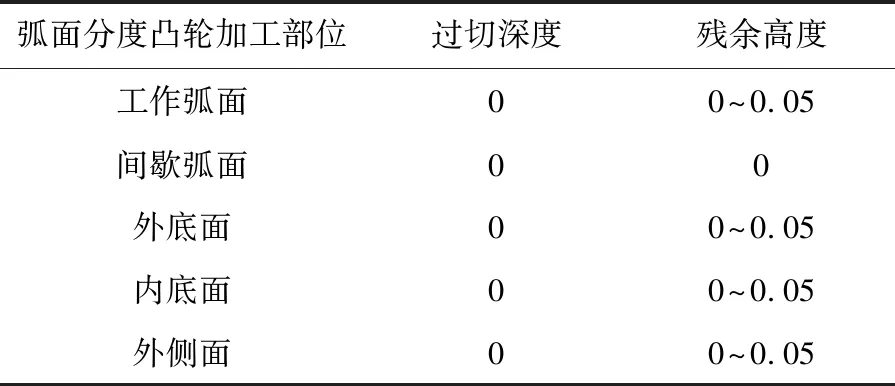
表4 弧面分度凸轮仿真加工分析比较 单位:mm

图10 凸轮加工残余高度对比分析

5 结束语

本文构建了圆柱滚子弧面分度凸轮廓面通用方程,基于MATLAB与NX 12.0快速准确地建立凸轮三维实体模型。采用自由曲面法进行五轴侧铣加工编程,并在VERICUT软件中进行虚拟仿真加工与分析,实现了圆柱滚子弧面分度凸轮的无图纸设计与制造集成化。仿真结果表明,该加工方法下凸轮整体加工误差处于设定的允差0.05 mm范围内,且在凸轮设计、编程以及仿真加工过程中机床、刀具、专用夹具及零件之间无过切情况,证明了加工刀轨的准确性,对于圆柱滚子弧面分度凸轮设计、仿真、加工一体化具有一定的借鉴与指导意义。