基于网络差分组合导航的AGV开发

高小栋,楼佩煌,钱晓明,张 悦,张沪松

(1.南京航空航天大学机电学院,江苏 南京 210016) (2.南京航空航天大学苏州研究院,江苏 苏州 215000)

自动导引车(automated guided vehicle, AGV)是装备有传感器和导航系统的能够沿预设路径自动行驶,具有搬运、移载等功能的无人运输车辆,由于其具有灵活、高效、自动化程度高的特点,在物流业、制造业中得到了广泛应用[1]。目前AGV的应用场景大多为在仓库、车间等室内环境中自动化运送物料。随着AGV技术的不断发展,其在非制造业中的应用占比也逐渐上升[2],例如园区中的物料运送,港口中集装箱自动化运输,机场中行李车、餐食车的无人化运行[3]等。这些运行场景大多为室外环境。但是在室外环境中,传统AGV所依赖的磁导航或色带视觉导航的导引方式存在更改路径困难、地标易磨损等缺陷[4]。曹西京等[5]研究了基于RTK-GPS技术导航的AGV,证明了其具有不依赖现场导引标志、部署方便、路径灵活不受限制、后续无需维护等优点;Kang等[6]研究了基于GPS的AGV航位推算算法,证明了在建筑或树木遮挡卫星信号的情况下,AGV仍能通过航位推算在一定时间内保持可用的定位精度。

路径跟踪控制算法是AGV系统的关键技术。任斌等[7]设计了基于色带和二维码的导航系统,建立了角度误差模型,基于PID算法,通过判断误差阈值进行差速AGV的转向控制;康照奇等[8]研究了基于预瞄点控制方法的AGV路径跟踪技术,通过设置预瞄点并基于AGV的运动学模型计算AGV通过该预瞄点时的控制参数,具有路径跟踪计算简单、鲁棒性较强的优点,但是在转弯时会出现路径内切现象,且算法中未考虑对AGV航向角的跟踪,路径跟踪精度较低。线性二次调节器(linear quadratic regulator, LQR)控制算法是针对现代控制理论提出的以状态空间形式给出的线性系统的控制算法,是一种典型的多目标优化最优控制算法[9],目前被广泛应用于无人驾驶领域的路径跟踪控制算法中[10]。

本文研发了一种基于网络差分组合导航定位的、应用于室外园区场景下的AGV,研究了基于LQR的路径跟踪控制技术以提高路径跟踪精度,并基于Ubuntu18.04和ROS Melodic系统编写了对应的控制系统软件。

1 系统组成

1.1 硬件系统

本文基于网络差分组合导航的AGV硬件系统主要由车体、网络差分组合导航系统和工控机组成。负载为一台六自由度对接机器人。硬件系统架构如图1所示。

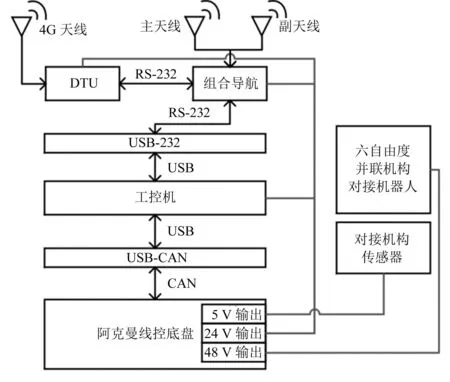
图1 硬件系统架构

由于室外园区场景的路面条件与工业厂房室内的路面条件相比较差,这就要求AGV能够在室外有轻微起伏的沥青或水泥路面上行驶,同时车轮应具有一定的耐磨损性能。园区场景范围较大,对AGV的续航里程和速度也有一定要求,因此选用商业化线控底盘作为AGV车体基座。通过标准CAN通讯接口实现对车体的转向电机、驱动电机、制动电机等模块的控制。

组合导航系统选用商业化组合导航模块、DTU(data terminal unit)模块和网络差分服务模块。组合导航模块通过卫星定位系统对车辆进行定位后,DTU模块通过移动网络连接差分服务供应商的服务器,将差分信息发送至组合导航模块进行差分定位,从而实现对AGV的厘米级定位。各模块参数见表1,其中组合导航的频点为四星十三频,DTU的网络制式为4G全网通,通讯接口为RS-232/RS-485。实物图如图2所示。

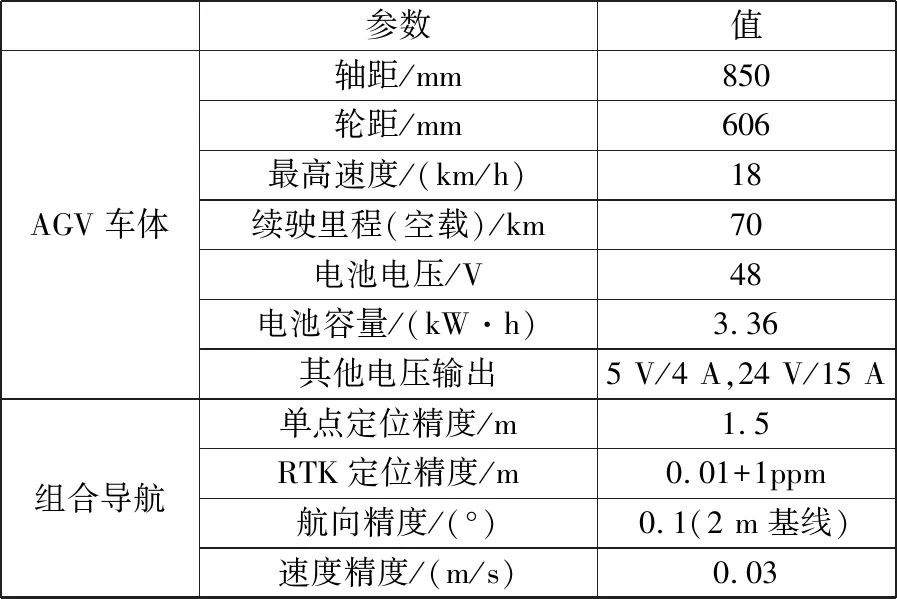
表1 硬件系统参数表

图2 基于网络差分组合导航的AGV

1.2 软件系统

本文所研发的AGV使用工控机作为上位机,运行Ubuntu18.04和ROS melodic系统。软件系统架构由上到下分别为感知层、控制算法层和驱动层,除此之外还有仿真工具和车辆模型模块。

感知层包括基于网络差分组合导航的车辆位姿信息解算程序,参考路径读取、记录和处理程序;控制算法层包括基于LQR的路径跟踪控制程序;驱动层包括各硬件设备的驱动和解算程序;仿真工具和车辆模型包括获取仿真环境下车辆位姿信息的程序和将控制指令发布至仿真环境的程序,以及其他必要车辆模型文件和参数文件等。具体各个程序节点之间的关系如图3所示。

图3 软件节点关系图

2 基于网络差分组合导航的AGV运动学建模

2.1 网络差分组合导航定位原理

传统卫星定位系统存在星历误差、时钟误差、电离层与对流层延迟、多路径效应、接收机固有噪声误差等各种误差,单点定位精度级别为10 m级;常使用载波相位差分技术减小误差。一种常用的算法为三差法[11],如图4所示。

图4 三差法进行差分

网络差分即把传统意义上需要自行建设的差分基站取消,改为使用由差分服务提供商建立的基站网络。差分服务提供商将所有基站的信息通过Ntrip标准协议上传至公网,车载端的车载DTU模块通过4G移动网络连接至差分服务提供商的端口获取离车辆最近的基站差分信息,从而进行高精度的差分卫星定位。

2.2 基于运动学的LQR路径跟踪控制算法

2.2.1AGV运动学模型建立

本文所研发的AGV的底盘为阿克曼转向式线控底盘。对车辆模型进行简化,忽略车辆在Z轴方向的平动,并且忽略悬架的影响,认为四个车轮与车体是刚性连接的,并将四轮模型简化为两轮模型,得到如图5所示的两轮运动学模型。图中,XOY为大地坐标系,φ为航向角,l为车辆轴距,vr为车辆后轮的速度,vf为前轮的速度,δ为前轮的转角,O′为转向中心,(Xr,Yr)为后轴坐标,ω为横摆角速度。

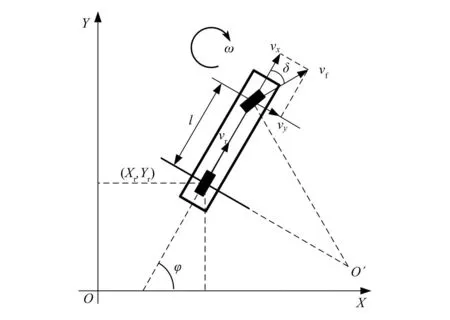
图5 两轮运动学模型

根据运动学关系进行计算,可以得到如式(1)所示的运动学约束关系。

(1)

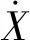
设车辆当前状态矩阵为ξ=[XYφ]T,目标状态矩阵为ξref=[XrefYrefφref]T,控制矩阵为u=[vrδ]T,目标控制矩阵为uref=[vrrefδref]T。其中,X、Y分别为车辆的X轴坐标和Y轴坐标;Xref、Yref、φref分别为车辆的目标X轴坐标、目标Y轴坐标和目标航向角;vrref、δref分别为目标后轮速度和目标前轮转角。显而易见,车辆的状态量和控制量是非线性关系,无法写成矩阵相乘的表达方式,可将其写为:

(2)

(3)

设车辆状态误差为Δξ,则有:

(4)

x设输入控制量的误差为Δu,由于控制目标为使车辆按照参考轨迹行驶,并不对车辆在参考轨迹上的速度和转角进行要求,因此可认为控制矩阵中的vrref和δref为0,即

(5)

将式(4)、(5)代入式(3)并进行变形,可以得到最终车辆模型的线性化运动学方程:

(6)

计算机运算和控制以及传感器采集的信息均为离散化的,通过前向欧拉法对式(6)进行离散化,可得到离散化后的运动学方程:

(7)

2.2.2LQR路径跟踪控制算法

LQR路径跟踪控制算法通过对系统累计误差进行累加构造损失函数J,并求得损失函数J的最小值进而求得最优的状态反馈控制器K,从而达到最优控制的目的。路径跟踪误差模型如图6所示。

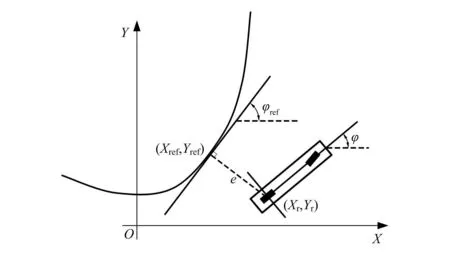
图6 基于运动学的路径跟踪误差模型

设车辆在第k个采样周期时的状态误差矩阵为Δξk,控制误差矩阵为Δuk,为使得累计误差最小,将车辆整个工作时间内的所有误差进行累加,构造如式(8)所示的损失函数,当求得损失函数J的最小值时,即可求得最优控制量。

(8)

式中:Q为状态误差矩阵的权重矩阵,R为控制误差矩阵的权重矩阵,Q和R均为对称矩阵。

考虑前n个采样周期的输入值和前(n-1)个采样周期的输出值,将式(8)进行变形可得:

(9)

应用拉格朗日乘子法对变形后的函数J求在车辆运动学公式约束下的极小值,进一步对式(9)变形可得:

(10)

式中:λ为拉格朗日乘子。

为简化公式,设:

(11)

则式(10)变形为:

(12)

(13)

式(13)中,由式④可求得λn,将结果代回式(13)递推可求得λn-1至λ0。设λk=2PkΔξk(k=1,2,…,n),由递推关系可得:

(14)

式中:P为过程矩阵,I为单位矩阵。

式(14)即为黎卡提方程。将结果代回式(13)中的式②,有:

(15)

反馈控制器为K,则有:

(16)

至此,得到计算车辆最优控制量的表达式。

3 实验验证

3.1 参考路径采集

手动遥控车辆行驶并记录位置和航向信息,采集一条路径,使用窗口滑动滤波方法进行路径平滑处理,得到参考路径,将其作为后续实验的目标路径。

3.2 仿真实验验证

根据上文基于运动学的LQR路径跟踪控制算法原理,编写对应控制节点,算法流程如图7所示。

图7 基于运动学的LQR路径跟踪控制算法流程图

读取参考路径的话题消息,启动LQR控制节点和仿真模块进行仿真,并将其与基于预瞄的路径跟踪算法对比,得到如图8所示的路径跟踪控制效果。从图中可以直观看出,LQR路径跟踪效果优于基于预瞄的路径跟踪效果。

图8 仿真路径跟踪控制效果

进一步通过路径跟踪误差模型计算其路径跟踪误差和航向角跟踪误差,并将其与基于预瞄的路径跟踪控制算法结果进行对比,结果如图9和图10所示。基于预瞄的路径跟踪算法平均路径跟踪误差el1=0.368 m,平均航向角跟踪误差eφ1=0.111 rad(6.36°);基于LQR的路径跟踪算法平均路径跟踪误差el2=0.179 m,平均航向角跟踪误差eφ2=0.078 rad(4.47°)。后者明显优于前者。

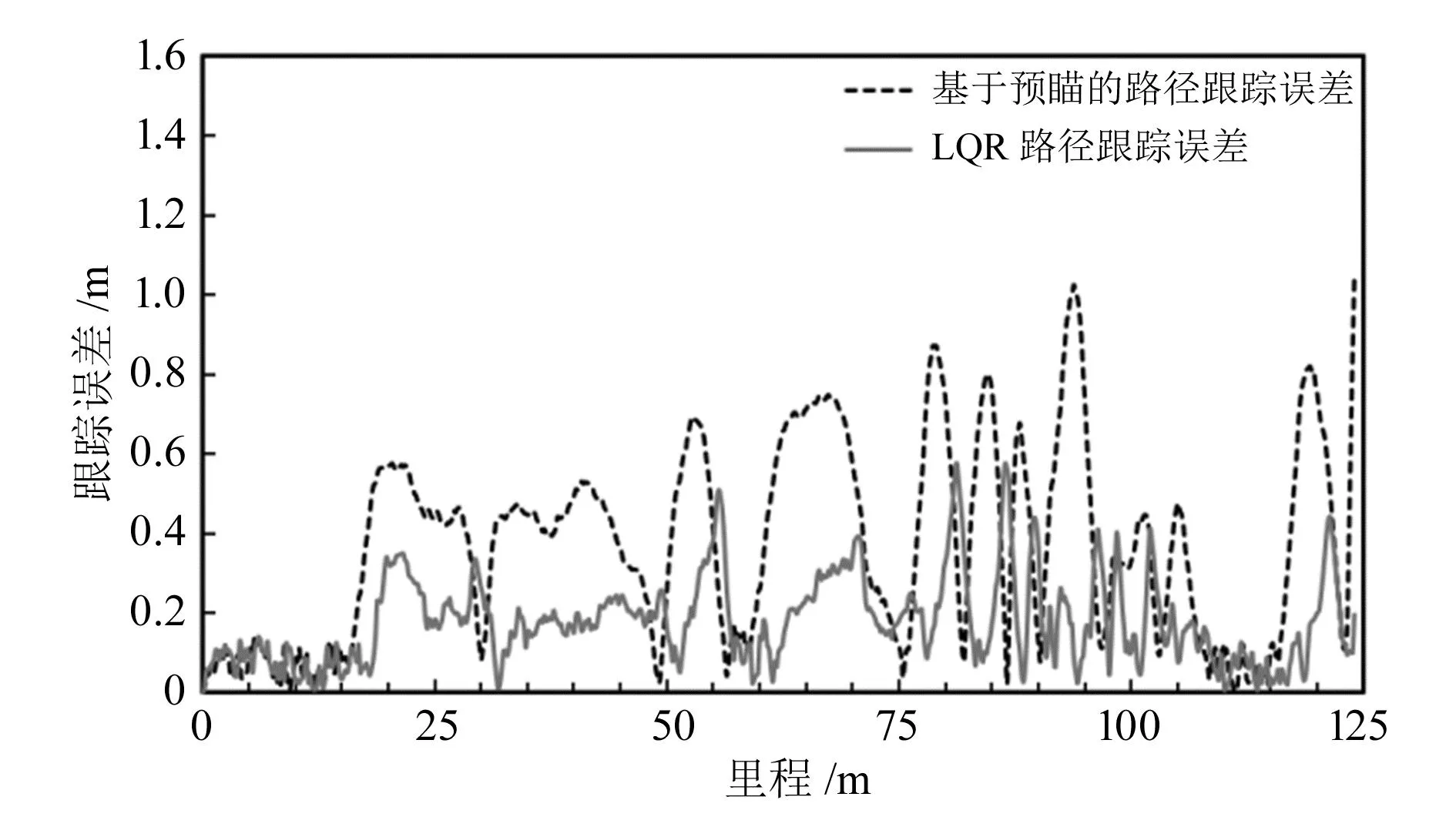
图9 仿真路径跟踪误差

图10 仿真航向角跟踪误差

3.3 实车实验验证

在室外选择一空旷地,使用上述手动采集的参考路径作为目标路径,进行实车实验并对两种算法结果进行对比,如图11所示。

图11 实车路径跟踪控制效果

从图中可以明显看出,基于预瞄的路径跟踪控制会在转弯时出现明显的内切现象,而基于LQR的路径跟踪控制在路径的前半段可以较好地完成路径跟踪,而在后半段路径曲率快速变化的路段,由于其本身算法特性,出现了超调现象。进一步对比二者的路径跟踪误差和航向角跟踪误差,结果如图12和图13所示。

图12 实车路径跟踪误差

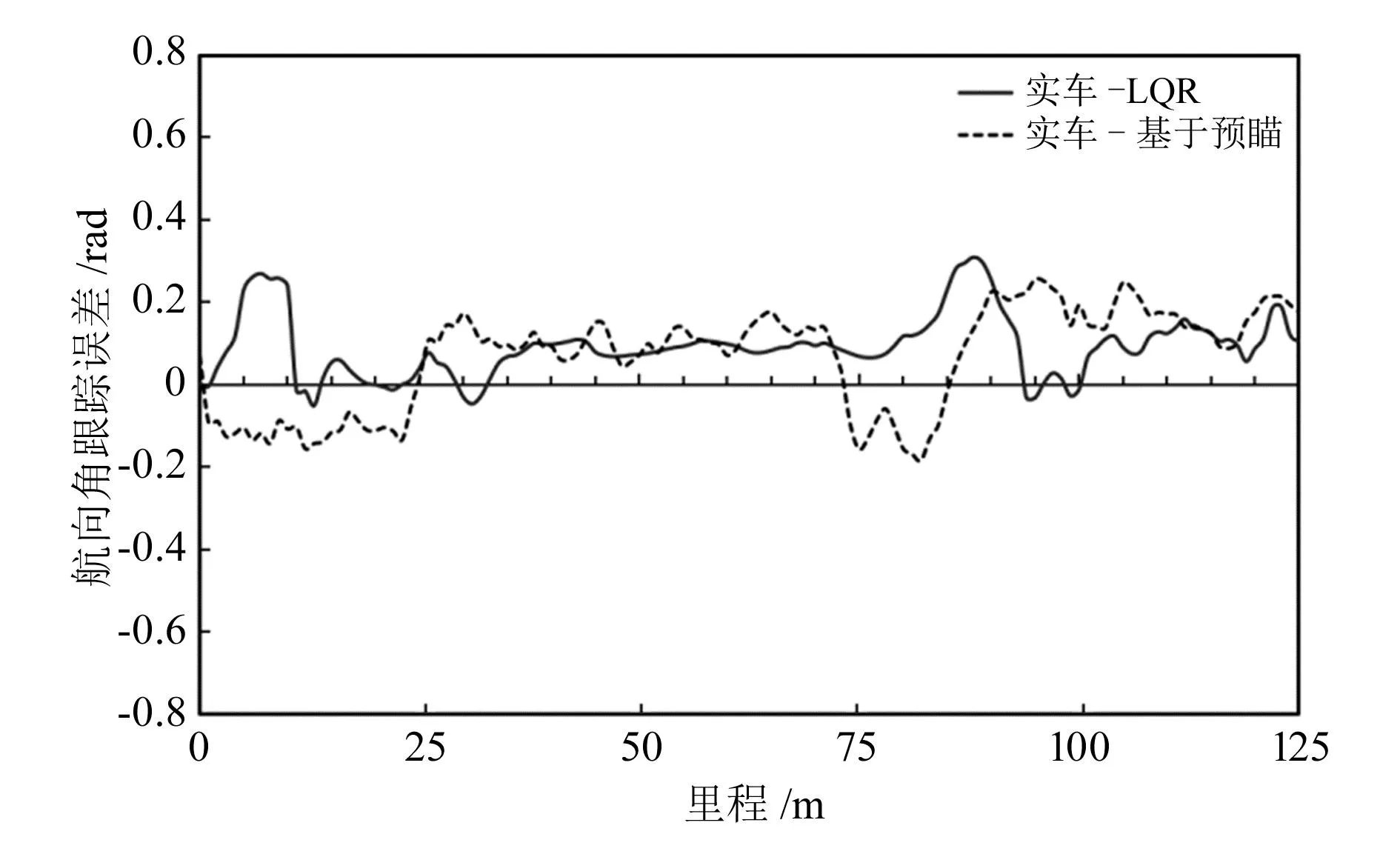
图13 实车航向角跟踪误差

在整段路径跟踪中,基于预瞄的路径跟踪算法平均路径跟踪误差el1=0.266 m,平均航向角跟踪误差eφ1=0.179 rad(10.26°);基于LQR的路径跟踪算法平均路径跟踪误差el2=0.216 m,平均航向角跟踪误差eφ2=0.117 rad(6.70°)。后者明显优于前者,与仿真结果相符。

4 结束语

本文研发了一台在园区室外环境下运行、基于网络差分组合导航的AGV,借助Ubuntu18.04和ROS Melodic系统开发了基于LQR的路径跟踪控制算法和对应的仿真环境,并将算法与传统基于预瞄的路径跟踪控制算法进行了仿真和实车的对比。实验结果表明,基于网络差分组合导航可以在园区室外场景中对AGV精确定位,基于LQR的路径跟踪控制算法可以使AGV实现路径轨迹和航向角的精确跟踪,且效果优于基于预瞄的路径跟踪算法。

本AGV适用于园区内的物料运送、巡检等场合。