水下航行器有限时间滑模控制
2024-01-13石泽林王孟军刘平安
褚 悦 ,石泽林 ,王孟军 ,2 ,刘平安
(1.哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨,150001;2.河北省双介质动力技术重点实验室,河北 邯郸,056017)
0 引言
速度是水下航行器的重要指标,超空泡航行器在水下运动时,大部分表面被超空泡包裹,构成了一种新的流体动力布局,极大地突破了速度屏障。空泡和水下航行器的位置关系可以分为航行器被空泡完全包裹和空泡闭合在航行器上2 种状态[1]。在实际水下航行中,航行器大部分时间处于不完全包裹状态(即空泡闭合在航行器上)。为了使航行器跟踪期望的轨迹,有必要研究不完全包裹状态下航行器的纵向平面控制。Semenenko 等[2]开创性地建立了水下航行器的六自由度模型和空化计算模型,阐述了水下航行器的动态特性。Lin等[3]验证了航行器动力学方程存在强非线性。Kirschner 等[4]简化了动力学模型,阐述了机动导航的稳定性和系统性能,说明了添加控制器的必要性,并设计了前馈-反馈控制器来实现水下航行器的机动控制。Li 等[5]研究了超空泡飞行器在垂直平面上的运动模型,分析了超空泡飞行器的动力学特性,提出了一种定深控制方法,将超空泡航行器高耦合非线性系统简化为线性系统,未研究系统不确定性和非线性的影响。Liu 等[6]针对浅水区全方位智能导航仪的跟踪控制采用反步设计技术,提出一种非线性输出反馈控制器,保证了系统全局指数稳定,但因为系统的不确定性,可能导致控制系统失稳。Fan 等[7]提出了一种由超空泡飞行器组成的高耦合非线性系统的模型预测控制策略,建立了基于牛顿定律的三自由度流体力学模型,仿真了该系统的运动特性,但鲁棒性较差。Li 等[8]建立了低速水下航行器的动力学模型,采用径向基函数(radial basis function,RBF)神经网络逼近和补偿未知函数,并采用反步法设计控制器,实现了航行器的定深控制,但未证明系统能在有限时间内快速收敛。Man 等[9]提出了一种基于RBF神经网络的鲁棒自适应滑模跟踪控制方案,采用自适应RBF 神经网络输出作为补偿参数,消除了系统不确定性的影响,实现了闭环控制系统的渐近误差收敛,但未能保证误差在有限时间内收敛。
文中贡献主要有以下三方面。
1) 采用独立截面膨胀原理[10]而非经验公式计算瞬态空泡形状[10],实时估算水下航行器的沾湿长度,从而准确计算浮力和相应力矩,提高动力学模型的精度。
2) 提出了一种有限时间滑模控制方法,使水下航行器快速跟踪给定深度,并使其他状态快速收敛。
3) 对于模型中的未知项,使用神经网络进行实时估计,并设计了相应的权重自适应律来描述神经网络权重随时间的变化规律。
1 水下航行器动力学模型
水下航行器受力及坐标系示意图如图1 所示。体坐标系的原点位于航行器的质心。Ox1轴沿航行器的轴线方向,Oy1轴垂直于航行器的轴线。

图1 超空泡航行器受力及坐标系示意图Fig.1 Forces acting on a supercavitating vehicle and coordinate system
水下航行器动力学模型为
式中:y为航行器的垂向位移;vy1为航行器沿体坐标系Oy1轴的速度;V为巡航速度;θ 为俯仰角;ωz为角速度;m为航行器质量;Jz为 航行器转动惯量;Fby1为航行器浮力在体坐标系Oy1轴的分量;Fcy1为空化器受力在体坐标系Oy1轴的分量;Ffy1为尾翼受力在体坐标系Oy1轴的分量;Mcy1,Mfy1分别为空化器和尾翼受力在体坐标系Oy1轴 分量的力矩;Mby1为浮力在体坐标系Oy1轴分量的力矩。
1.1 航行器空化器受力及其力矩
空化器受力的作用点位于空化器的中心,其作用在体坐标系Oy1轴上的分量为
对应力矩为
式中: ρ为水的密度;Rn为空化器半径;σ为空化数;Cx0为空化数为0 时空化器阻力系数;δc为空化器偏转角;xc为 航行器质心到空化器中心的距离。图2 显示了航行器空化器受力情况。

图2 空化器受力和偏转角示意图Fig.2 Forces acting on a cavitator and angle of deflection
1.2 航行器尾翼受力及其力矩
当尾翼的偏转角为正时,尾翼所受力在体坐标系Oy1轴 的分量Ffy1产 生的升力矩Mfy1与角速度的正方向相反,且
式中:S为超空泡航行器的特征面积,通常为航行器的最大横截面积;分别为升力系数和升力矩系数;δf为尾翼的偏转角;L为航行器的长度。
1.3 航行器所受浮力及其力矩
当航行器在水中航行时,只有一部分被浸没。为了确定航行器的浮力和浮力力矩,需要计算空泡形状,并使用独立截面膨胀原理确定浸没长度。
空泡形状的计算公式为
式 中: ∆p(τ,t)=p∞(τ,t)-pc(τ,t),其中,p∞(τ,t)为无穷远处的压力,pc(τ,t)为 空泡内部的压力,τ为空泡当前截面形成的时刻;k=4πCx/a2,其中,Cx为空化器阻力系数,a为介于2~2.5 之间的半经验常数;ρw为水的密度。
方程的初始条件为
式中,Dn为空化器直径。利用式(7)求解S和t之间的关系,则所有时刻任意位置的空泡半径和长度都能被求解出。
假设空泡的长度是lc,航行器浮力在体坐标系轴的分量为
假设浮力作用于浸没段的中点,相应的浮力在体坐标系轴分量的力矩为
定义状态变量x1=[y,θ]T,x2=[vy1,ωz]T,由于水下航行器在航行时俯仰角、空化器转角和尾翼偏角都很小,所以为了简化水下航行器的动力学方程,当以下角度较小时,可以近似认为 sinδc≈δc,sinθ ≈θ,cosδc≈1,cosθ ≈1,sinδf=δf,cosδf=1。其中: δc为 空化器转角;θ 为航行器俯仰角;δf为尾翼转角。
引入控制律u,水下航行器的动力学方程改为
2 水下航行器控制律设计
引理1[11]如果有一个连续可微的正定函数,满足
式中:c>0,b>0,0<α<1;U是原点附近的开邻域且U⊆D。那么系统是有限时间稳定的,稳定时间为
式中,x0是x的初值。
引理2[12]如果有一个连续可微的正定函数,满足
式中:c>0,b>0,0<α<1;U是原点附近的开邻域且U⊆D。那么系统是有限时间稳定的,x将收敛到一个小邻域内,稳定时间为
式中,θ0满 足0 <θ0<1。
将动力学方程重新写成如下形式
式中:f1=Ex1;f2=C+D。
定义跟踪误差
式中:x1d是x1的期望值,文中设计控制律的目的是让x1(t)跟 踪xd(t)。
为避免奇异性,将全集 Ω 分为 Ω1和 除 Ω1以外的ΩΩ1两 部分,收敛的邻域为 Ω1,整个空间除收敛的邻域外为 ΩΩ1,在 Ω上定义滑模面为
式中,c和b是正常数。
对于 ΩΩ1,即e包含于ΩΩ1,滑模趋近律可以被设计为
式中,c1和b1是正常数。
基于以上的滑模面和滑模趋近律,设计控制律为
定理1考虑水下航行器动力学系统(式(16))。通过控制律(式(20))在有限时间内将系统状态达到原点周围的小邻域。
证明: 将Lyapunov 函数定义为
Lyapunov 函数的导数为
因为b1>0,c1>0,根据定理1,滑模面s在有限时间内收敛到0 之后,跟踪误差将在时间T2内收敛到0,。总到达时间T=T1+T2。因为e1在有限时间内收敛到0,因此x1→x1d,应用设计的控制律(式(20))可以使水下航行器跟踪预定深度。
在式(16)中,由于一般情况下俯仰角、余弦值、相应的升力和升力矩系数难以获得,所以f2通常是未知项。而RBF 神经网络的特点是可以在不知道模型特性的情况下,实时估计模型的未知项,将估计值代入控制律作为补偿。
RBF 神经网络是一种3 层前向网络,包括输入层、输出层和隐藏层。从输入层到输出层的映射是非线性的,而从隐藏层到输出的映射是线性的。使用RBF 神经网络可以显著提高系统的精度、鲁棒性和适应性。
f2的估计值为
式中:w∗=[w1,w2,···]是神经网络的最优权重;hj(x)是隐藏层第j个节点的输出,x=[x1,x2]是RBF 神经网络的输入;ε是估计误差。
hj(x)的表达式为
式中:cj=[cj1,cj2,···]为隐藏层第j个节点中心点处的向量值;bj>0是隐藏层第j个节点高斯函数的宽度。
控制律和神经网络权重的自适应律设计为
假设1假定神经网络的估计误差和权重误差都是有界的,即
式中,η1,η2均为一个小的正数。
定理2考虑由式(16)描述的水下航行器动力学系统。通过在有限时间内依据控制律(式(25))和自适应律(式(26))使系统跟踪预定轨迹。
证明: 定义Lyapunov 函数为
根据定理2,滑模面收敛于紧集 Ω1,神经网络的估计权值在有限时间T3内收敛于最优权值的小邻域附近。
经过T3之后,滑模面收敛于0,根据定理1,跟踪误差在有限时间T2内收敛到接近0 的小邻域。系统收敛的总时间为T=T2+T3。因此,通过使用控制律(式(25))、自适应律(式(26))并适当选择参数,跟踪误差e1可以收敛到一个小的紧集,确保系统状态跟踪给定状态。
由于在 Ω1内 滑模面是有界的,且自适应律w˙ˆ 停止更新且初值有界,所以整个Lyapunov 函数(式(28))在 Ω1内 有界,假设上界为 ε1,那么有
即Lyapunov 函数在全局有界,这便完成了全局稳定性的证明。
最终得到航行器的控制律和相应的自适应律为
3 仿真结果与分析
水下航行器控制系统框图如图3 所示。验证文中设计的控制律(式(34))和自适应律(式(35))的有效性。计算所需的航行器动力学参数如表1 所示。仿真结果如图4~13 所示。

表1 水下航行器动力学参数Table 1 Dynamic parameters of undersea vehicle

图3 水下航行器控制系统框图Fig.3 Block diagram of undersea vehicle control system

图4 水下航行器深度跟踪曲线Fig.4 Depth tracking curve of undersea vehicle
计算初始条件为:y0=0.2 m;θ0=5.73◦;vy0=0.2 m/s;ω0=-34.38(◦)/s;w(0)为零矢量;γ=100;隐藏层宽度为b=0.9,隐藏层中心
期望轨迹为x1d=0.5+0.1sint,x2d=-(1/V)。根据实际要求,航行器空化器转角和尾翼转角需要在 35◦以内。
从图4 和图6 可以看出,在控制律(式(34))和自适应律(式(35))的作用下,水下航行器的深度和角度可跟踪期望轨迹。图10 和图11 显示了空化器角度和尾翼偏转角随时间的变化,其绝对值不超过4°和2°,表明输入有界。从图12 可以看出,滑模面在有限时间内收敛到接近零的小邻域。从图5 和图7 可以看出,在t=1.23 s 后,深度跟踪误差和角度跟踪误差均收敛在原点附近的小邻域内,表明系统具有良好的跟踪性能。图13 显示了估计值可在有限时间内收敛到其实际值周围的邻域。

图5 深度跟踪误差随时间变化曲线Fig.5 Curve of depth tracking error with time
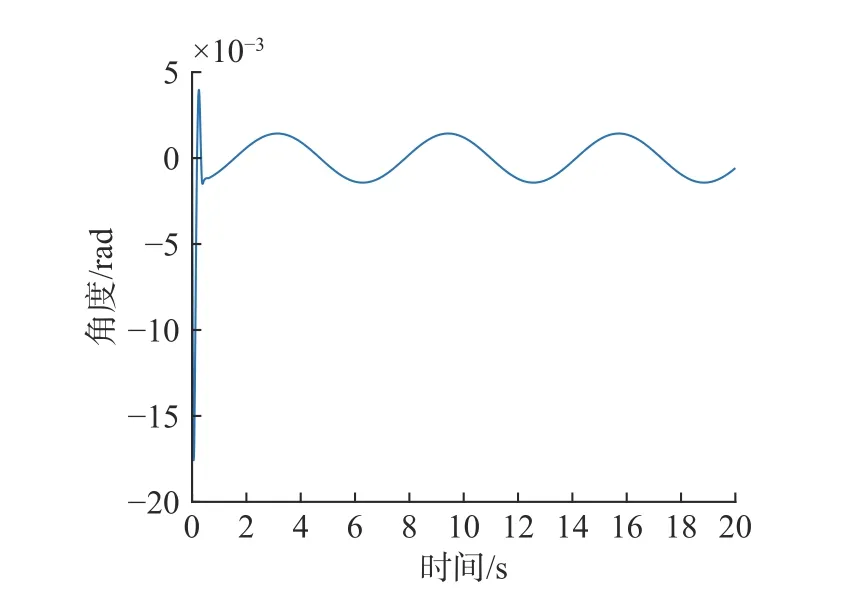
图6 水下航行器俯仰角跟踪曲线Fig.6 Pitch angle tracking curve of undersea vehicle

图7 俯仰角跟踪误差随时间变化曲线Fig.7 Curve of pitch angle tracking error with time

图8 角速度随时间变化曲线Fig.8 Curve of angular velocity with time
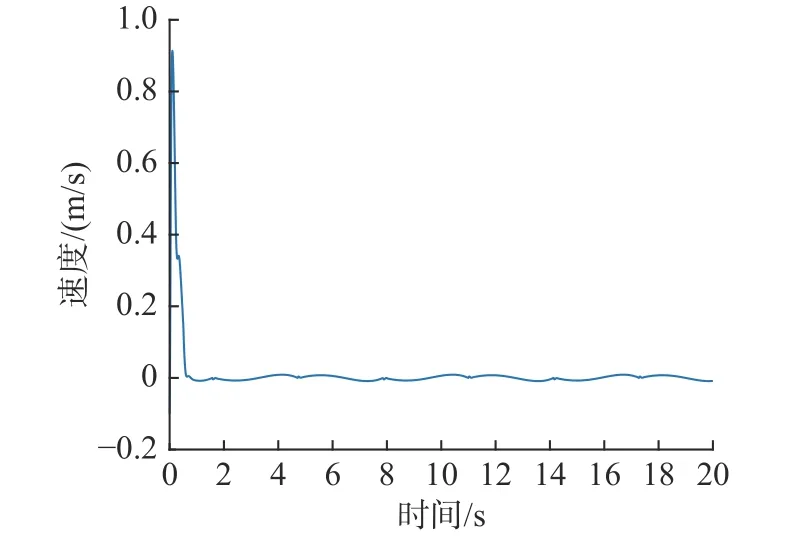
图9 垂向速度随时间变化曲线Fig.9 Curve of vertical velocity with time
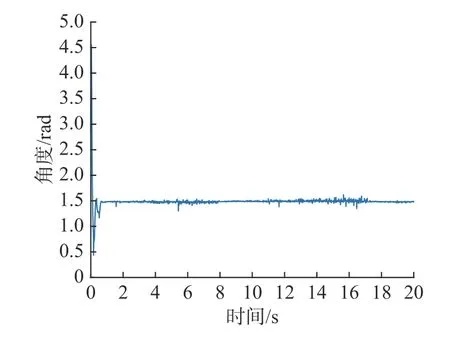
图10 空化器偏转角随时间变化曲线Fig.10 Curve of cavitator deflection angle with time

图11 尾翼偏转角随时间变化曲线Fig.11 Curve of tail deflection angle with time

图12 滑模面随时间变化曲线Fig.12 Curve of sliding surface with time
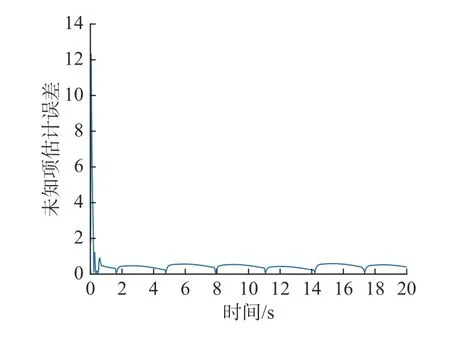
图13 未知项估计误差随时间变化曲线Fig.13 Curve of the estimation error of unknown term with time
4 结束语
文中提出一种有限时间滑模控制器来控制不完全包裹的水下航行器。RBF 神经网络用于估计动态方程中的未知项,并设计自适应律来更新神经网络的权重。利用Lyapunov 理论证明了动态系统的稳定性。最后,对水下航行器的水下运动进行了仿真。结果表明,所设计的控制律能使系统具有良好的跟踪性能,跟踪误差收敛到较小范围。因为水下环境复杂,可能出现执行器失效等一系列问题,需要在复杂环境下进行实验,进一步验证控制系统是否能达到预设目标。
