基于声-固-压电耦合的纵振水声换能器工艺研究
2024-01-13耿鹏飞田杜养刘小光程彩霞冀邦杰
耿鹏飞,田杜养,刘小光,程彩霞,冀邦杰
(中船西安东仪科工集团有限公司,陕西 西安,710065)
0 引言
纵振换能器是一种常用的大功率发射器,能够以较小的质量和体积获得较大的声能密度,从而广泛应用于超声和水声技术中。换能器的制造是设计、加工、装配与测试一体化耦合过程。由于水声换能器实际生产包括机械零件精密加工、陶瓷环筛选测试、陶瓷环涂胶粘接、换能器预紧装配以及匹配层灌注等复杂的工艺过程,故生产工艺环节对换能器的相关电声性能有一定影响。
针对在压电陶瓷、电极及前后盖板之间涂胶粘接问题,张福学[1]指出应用环氧树脂胶合可以更好地传递声波;阎福旺[2]论述了粘接的化学固化过程,并指出在固化过程中要对换能器进行加热加压处理,从实际换能器制作过程出发提出了胶粘剂对换能器性能的影响,但未对胶粘剂对换能器性能的具体影响程度进行分析及讨论;张庆辉等[3]对纵振换能器性能进行数值研究和仿真分析,分析过程未考虑胶粘剂对换能器相关性能的影响;莫喜平[4]指出对高频换能器的分析一般不可以忽略胶粘剂的影响,但在仿真中未给出相应考虑胶粘剂影响的换能器有限元模型,也未对具体影响程度进行分析。文中通过建立考虑胶粘剂的有限元模型,分析了胶粘剂涂抹对换能器在空气中电声性能的影响。
关于换能器压电陶瓷环之间同轴度对纵振换能器性能影响的文献较少,文中通过建立考虑压电陶瓷环之间同轴度的有限元模型,分析了压电陶瓷环同轴度对换能器谐振频率及发送电压响应的影响。
关于预应力对纵振换能器性能影响的文献已有大量研究,荣德新[5]主要分析了纵振压电换能器的预应力控制,张云电等[6]给出了基于计算机控制的压电换能器恒扭矩装配方法,但未能涉及预应力对换能器性能参数的影响;李军等[7]基于实验研究讨论了压电换能器共振频率与预应力的关系,给出了施加预应力的参考值,但未能给出预应力对纵振换能器水下相关性能参数的影响。文中通过理论计算给出了该换能器预应力加载的适宜范围,结合有限元仿真的方法,系统地研究了预应力通过影响压电陶瓷材料的压电性能参数,最终影响纵振换能器在空气和水中的相关性能,并结合实验验证了其准确性。
目前,水声换能器的研究方法主要有: 等效网络法、瑞利法、有限差分法和有限元法[8]。结合工程实际应用背景,针对换能器在生产过程中的工艺环节,建立了三维有限元模型,分析了装配过程中的相关因素对换能器的频率响应和发射电压响应的影响,系统研究了换能器装配工艺中涂胶、陶瓷环装配和预紧力施加过程,并制作了样机,进行了声学性能测试工作,获得了详细的声学数据。将仿真数据与测试数据进行了对比,详细分析了测试值与仿真值存在差异的主要原因。
1 基本理论
换能器本身存在集多物理场耦合在一起的复杂问题[9]。包括压-电耦合分析、声-固耦合分析和声-固-压电耦合分析。
系统的动力学方程为
式中:m为模态质量;c为模态刚度;d为模态阻尼;C为电容;R为电阻;α为机电转换因子;U为输入电压;Q为输入电荷;u为模态位移;FV为预紧力负载。
声-固耦合在水域和换能器前辐射头界面处的边界上起作用,在边界上建立双向耦合。将前幅射头的振动加速度用作声源,在流体域中进行传播。由压力声学计算得到的流体压力作为反作用力施加在前辐射头上。
声压分布的波动方程为
式中: ρ为密度;k为常数;P为声压。
仿真使用稳态研究步骤求解静态应力分布。将该步骤得出的解作为线性化点,用于求解频域扰动研究步骤中的振动问题。
1.1 涂胶粘接
换能器在实际装配过程中,前盖板、压电陶瓷环、电极引片和后质量块端面均用毛刷涂抹环氧树脂后依次粘接,粘接完成后施加预紧力,随后用绸布将换能器外侧周围挤压出的残胶擦拭干净。经测量,胶层固化后零部件接触表面粘接层厚度为0~0.02 mm。为了保证更好的粘接性能,在电极引片上设计多个均布的通孔,通孔处胶层厚度为0.15 mm。压电陶瓷环内侧依然存在残胶,残胶厚度为0.2~0.5 mm。
建立考虑粘接层、残胶层及电极引片的压电换能器模型,用于分析涂胶粘接对换能器相关电声性能的影响。带粘接层的1/6 换能器局部模型结构如下: 粘接层—电极引片—粘接层—压电陶瓷层—粘接层—电极引片—粘接层,残胶层位于压电陶瓷环内侧,如图1 所示。
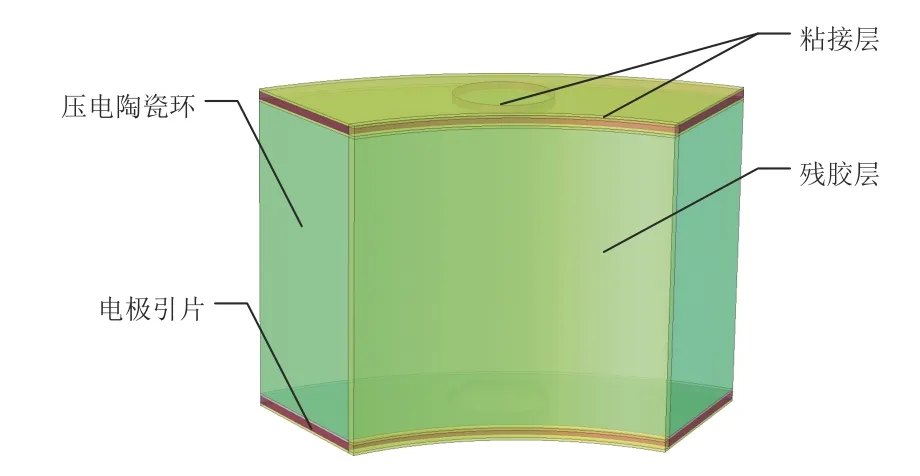
图1 带粘接层的1/6 换能器局部模型示意图Fig.1 1/6 transducer model with an adhesive layer
1.2 结构件之间同轴度
换能器在装配过程中,压电陶瓷、电极引片、前盖板和后质量块通过预紧力螺栓串联在一起,由于装配过程为操作人员手工操作,故装配完成后很难保证所有零件在同一轴线上,导致实际装配模型和理论计算模型存在差异,故换能器相关性能也与理论值发生偏差。文中通过调整陶瓷环装配,同轴度模拟实际装配过程中陶瓷环装配存在同轴度误差的现象,分析装配同轴度对换能器电声性能的影响。
1.3 螺栓预紧力
依据纵振换能器的结构,换能器在给定声功率发射时,节面所受的最大应力远小于所施加的预紧力,故只结合预紧力对螺栓强度和压电陶瓷性能的影响,给出该换能器预紧力加载的合适范围。
考虑预紧力对螺栓的强度影响,文中使用的预应力螺栓采用2Cr13 马氏体不锈钢材料先淬火后回火。由于换能器结构会受到动载荷的影响,所以螺栓预紧力应适当调低,选择在其屈服载荷的35%左右最为合适,最多不能超过70%。
螺栓预紧力为
式中:K1为预紧力系数,一般情况下为0.35~0.7;σS为 螺栓材料的屈服点;A1为螺栓应力横截面积。
考虑预紧力对压电陶瓷性能的影响,预紧力太小会导致各零件间接触刚度下降,损耗增加,机电转换效率下降,预紧力太大会导致压电材料退极化。文中使用的材料本构模型基于实验结果。该模型采用方法类似于文献[10]描述方法,其中材料的压电常数取决于压电材料上的标称FV,其值在 50 MPa 的预紧力下归一化。材料的压电属性随压电材料预紧力的变化如图2所示。

图2 压电常数随预紧力变化Fig.2 Variation of piezoelectric constants with pretensioning force
陶瓷环预紧力为
式中: σt为压电陶瓷环受到预紧力时内部预应力,一般情况为30~70 MPa;A2为压电陶瓷环横截面积。
螺栓拧紧力矩为
式中:K2为螺栓拧紧力矩系数,根据机械设计手册选取该系数为0.15;d为螺纹公称直径。
经计算F1=6.3~12.6 kN,F2=5.1~11.9 kN,故选取FV=6.3~11.9 kN,M=5.7~10.7 N·m。
2 模型简介及有限元建模
2.1 基本模型
换能器基本模型如图3 所示,主要包括前盖板、陶瓷环、质量块、匹配层以及预紧力螺栓等。
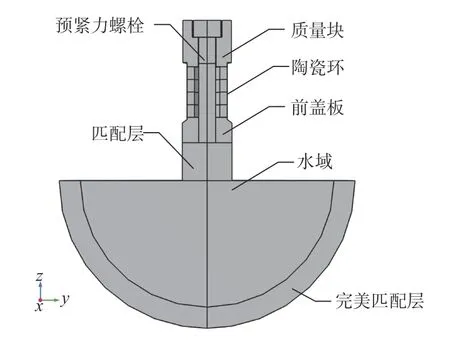
图3 换能器三维模型Fig.3 3D model of transducer
为了计算无限水域的声学特性,采用完美匹配层(perfect matched layer,PML)来构建一个封闭空间域,当散射波到达PML 时会被迅速吸收,形成一个无反射边界,从而不会影响空间内的散射声场[11]。
2.2 材料模型
带匹配层纵振换能器前幅射头采用2A12,材料密度2 780 kg∙m-3,弹性模量为70.3 GPa,泊松比为0.345。后质量块和预应力螺栓采用2Cr13,材料密度7 850 kg∙m-3,弹性模量为210 GPa,泊松比为0.3。电极引片采用H62,材料密度8 960 kg∙m-3,弹性模量为110 GPa,泊松比为0.35。匹配层采用环氧树脂基复合材料,材料密度1 500 kg∙m-3,弹性模量为7.6 GPa,泊松比为0.46。压电陶瓷环采用PZT-4 材料,材料密度为7 500 kg∙m-3,材料弹性常数、压电应力常数和相对介电常数见表1[12-13];粘接层材料密度为1 700 kg∙m-3,弹性模量为10 GPa,泊松比为0.38。
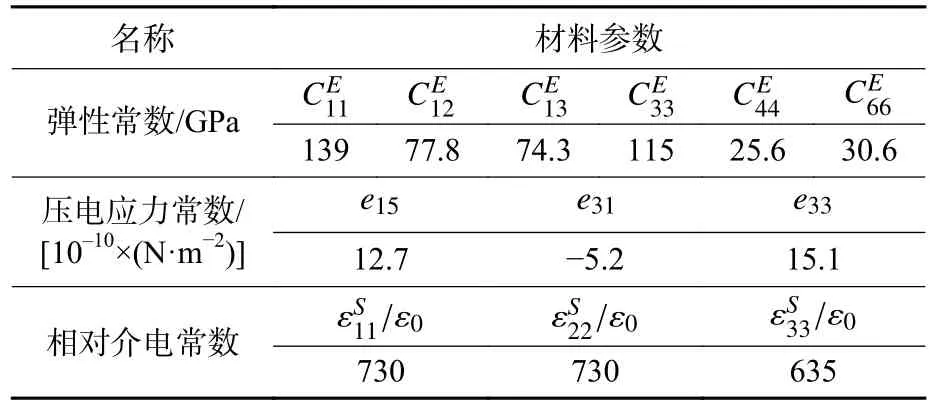
表1 PZT-4 材料参数Table 1 PZT-4 material parameters
2.3 网格划分及边界条件设定
为了精确解析水域中的声压波,需要将水域中最大网格单元大小定为最小波长的 1/5,则有
式中:V水=1 500 m/s 为水中声速;fmax=50 kHz为换能器最大扫描频率。
为了使网格平滑过渡,对固体域采用四面体网格划分,最大网格尺寸为Lmax。对PML 创建5 层结构化网格。在邻近外场边界的内水域内创建边界层网格,该层的厚度设为Lmax的 1/4,该边层在内部自由四面体网格与外部结构化棱柱网格单元之间产生平滑过渡,从而使外场计算的精度更高。该网格模型共计5.8 万网格单元,16.4 万求解自由度。该有限元网格模型如图4 所示。
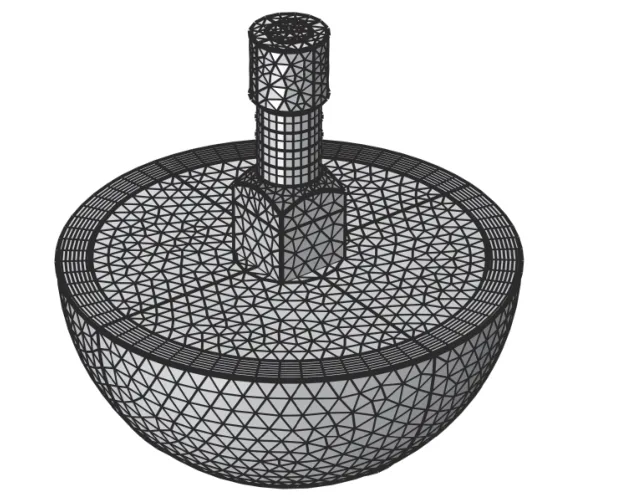
图4 网格模型Fig.4 Mesh model
电压边界: 在对应的压电陶瓷电极面施加电压边界条件,箭头表示极化方向,其中2 个压电陶瓷环沿+Z 向极化,另外2 个沿-Z 向极化,正负极之间电压为1 V,如图5所示。
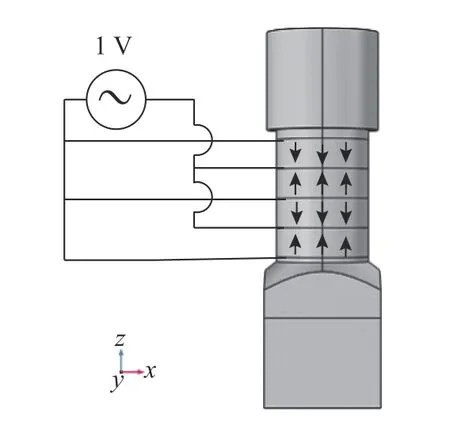
图5 压电陶瓷环极化方向和电连接示意图Fig.5 Polarization direction and electrical connection of piezoelectric ceramic ring
预紧力边界: 螺栓安装在装置上用于固定各个部件,螺栓拧紧过程会产生一个反作用力,表现为螺栓上的预紧力。由此产生的预应力有助于在装置的正常工作期间将螺栓保持在固定位置。根据实际装配过程建立接触对并对预紧力截面施加拧紧力矩。
阻尼边界: 在15~50 kHz内施加瑞利阻尼,定义阻尼系数为0.005。
位移边界: 由于换能器在整个工作过程为自由状态,故设定换能器空间自由度为6。
3 数值计算结果分析
3.1 涂胶粘接对换能器性能的影响
对换能器进行频域分析,得到分别考虑粘接层、残胶层的换能器模型在空气中的电导随频率变化的有限元仿真对比曲线,如图6 和图7 所示,可以看出无粘接层和无残胶层的理想换能器模型匹配前谐振频率为26.85 kHz,带粘接层的换能器模型匹配前谐振频率为26.55 kHz,带残胶层的换能器模型匹配前谐振频率为26.92 kHz,而3 种换能器模型谐振频率处的电导值变化较小。

图6 空气中粘接层对换能器电导影响仿真曲线Fig.6 Simulation curves of the effect of adhesive layer on conductivity of transducer in air
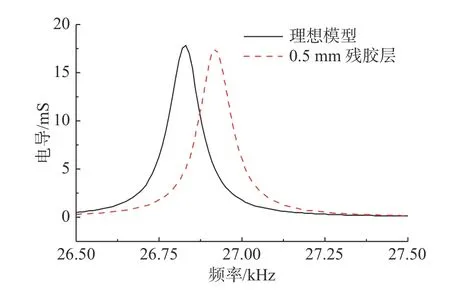
图7 空气中残胶层对换能器电导影响仿真曲线Fig.7 Simulation curves of the effect of residual glue layer on conductivity of transducer in air
3.2 装配同轴度对换能器性能的影响
对换能器进行频域分析,得到2 种轴度下电导随频率变化的有限元仿真对比曲线,如图8 所示。
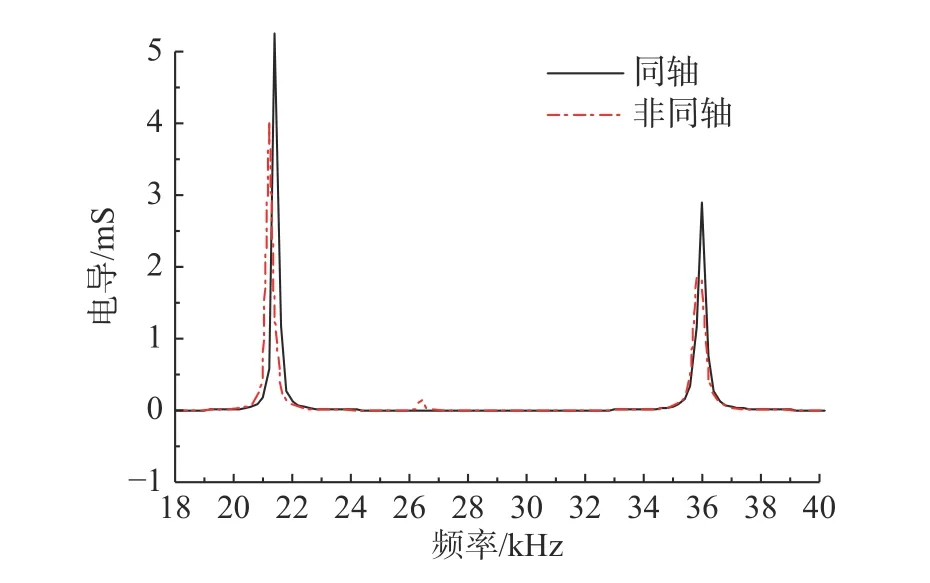
图8 空气中同轴和非同轴换能器电导随频率变化仿真曲线Fig.8 Simulation curves of conductivity with frequency of coaxial and non-coaxial transducers in air
图8 和表2 中,同轴模型的换能器电导值比非同轴模型的换能器电导值高20%,且曲线光滑无毛刺。同轴度对换能器的固有频率值影响可以忽略。

表2 空气中同轴和非同轴换能器性能参数Table 2 Performance parameters of coaxial and noncoaxial transducers in air
图9 给出了同轴模型和非同轴模型匹配层换能器在水中发送电压响应(transmitting voltage response,TVR)曲线。可以看出,非同轴模型相比同轴模型TVR 降低约0.4~0.8 dB,此外,由于同轴度误差的存在,换能器的1 阶谐振频率和2 阶谐振频率之间出现了2 处明显的毛刺。

图9 水中同轴和非同轴换能器TVR 随频率变化仿真曲线Fig.9 Simulation curves of TVR with frequency of coaxial and non-coaxial underwater transducers
3.3 预紧力对换能器性能的影响
建立预紧力模型,模拟实际装配过程中施加预紧力的过程,分析预紧力对换能器性能的影响。
图10 为带匹配层换能器分别施加5.7、10.7 N·m的预紧力后其中的静应力分布图。可以看出,螺栓杆中的应力分布均匀,最大应力主要出现在螺栓杆以及螺栓正下方的后质量块中心部分。

图10 2 种预紧力下换能器中应力分布Fig.10 Stress distribution in transducers under two pretensioning forces
图11、图12 和表3 给出了施加2 种预紧力后换能器在匹配前后空气中的电导随频率的变化情况。换能器谐振频率和谐振频率处的电导随着预紧力增大而增大。换能器匹配前预紧力从5.7 N·m增大到10.7 N·m,谐振频率增加1 kHz,谐振频率处电导增大8%,匹配后1 阶谐振频率增加0.6 kHz,电导增大51%;2 阶谐振频率增加0.2 kHz,电导增大13%。
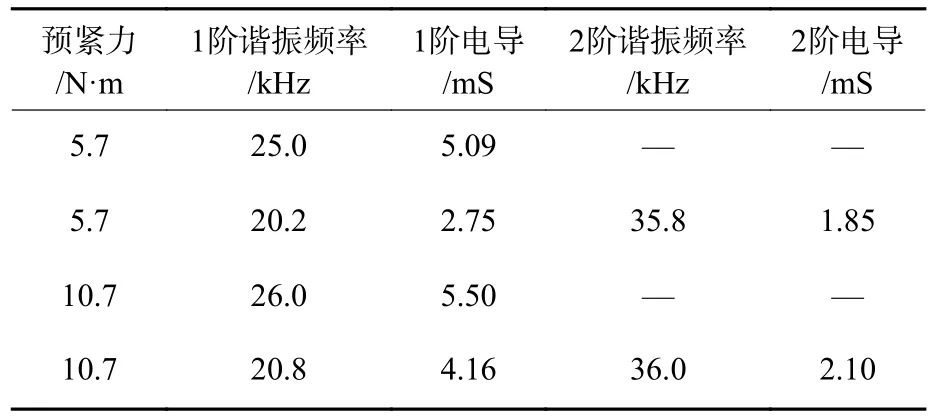
表3 空气中2 种预紧力下换能器性能参数列表Table 3 Performance parameters of transducer under two pre-tensioning forces in air

图11 空气中2 种预紧力下换能器电导随频率变化仿真曲线Fig.11 Simulation curves of conductivity with frequency of transducer under two pre-tensioning forces in air
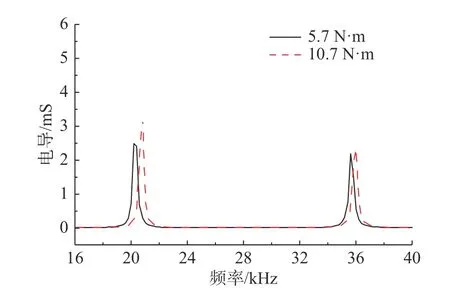
图12 空气中2 种预紧力下匹配层换能器电导随频率变化仿真曲线Fig.12 Simulation curves of conductivity with frequency of transducer with a matching layer under two pre-tensioning forces in air
图13 给出了水中2 种螺栓预紧力下,TVR 随频率的变化,由曲线变化可以看出,随着施加预紧力的增大,2 阶固有频率均增大;1 阶固有频率处TVR 降低,2 阶固有频率处TVR 升高,TVR 曲 线更加平坦。换能器在施加10.7 N·m 预紧力后20~34 kHz 相对平坦的区域适用于传感应用。

图13 水中2 种预紧力下TVR 随频率变化曲线Fig.13 Simulation curves of TVR with frequency under two pre-tensioning forces in water
4 实测结果与分析
4.1 实验测试方法
首先制作无胶装配的换能器实物。经过静置及高温去除应力后进行测试,随后将换能器拆解并进行涂胶装配,通过装配后换能器的高度保证粘接层厚度,再经过静置及高温去除应力后进行测试,以验证粘接层对换能器电声性能影响;采用胶枪喷涂(无残胶)和毛刷涂抹2 种涂胶方式制作了不同的换能器,通过装配后的质量估算陶瓷环内部残胶层的厚度,经固化及去应力后进行测试,以验证残胶层对换能器电声性能的影响;通过设计专用的换能器装配工装保证陶瓷环的同轴度,用以对比工装装配和手工装配时不同同轴度对换能器电声性能的影响;通过力矩扳手对换能器施加不同的预紧力,制作2 种预紧力下换能器实物,以验证预紧力对换能器电声性能的影响;最后将换能器前辐射面硫化后进行水池测试。试验制作部分换能器实物如图14 所示。

图14 压电换能器实物Fig.14 Physical piezoelectric transducer
4.2 实测分析
用4294A 阻抗分析仪在空气介质中对匹配层灌注前后换能器的电导进行了测试,将制作好的换能器进行硫化,保证其密封性,然后在消声水池进行声性能测试,其结果如图15~图19 所示。
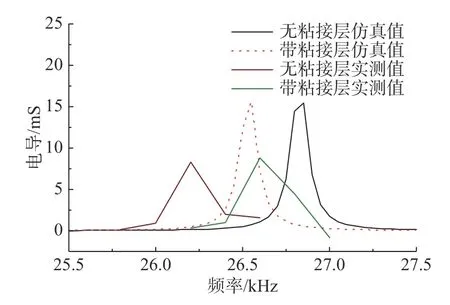
图15 粘接层对换能器电导影响的仿真与实验对比Fig.15 Comparison of simulation and experimental data on effect of adhesive layer on conductivity of transducer
图15 可以看出,实际制作出的换能器无论是否涂抹粘接剂,其谐振频率及电导值均小于仿真值;仿真计算中,在换能器模型加入粘接层后,其谐振频率降低了约0.3 kHz;而实际测试中,加入粘接层后,其谐振频率升高了约0.4 kHz。无论是仿真计算还是实际测试,粘接层对谐振频率和电导值的影响都比较小。
图16 可以看出,残胶层使换能器的谐振频率升高,但对电导值影响较小。

图16 残胶层对换能器电导影响的仿真与实验对比Fig.16 Comparison of simulation and experimental data on effect of residual glue layer on conductivity of transducers
图15 和图16 中粘接层和残胶层均通过影响陶瓷环来影响换能器的电声性能。陶瓷环的谐振频率方程为
式中:f为谐振频率;E为弹性模量;r2为陶瓷环外径;r1为陶瓷环内径;d33为轴向压电常数;h为厚度。
粘接层通过填补各零件端面间的微小空隙来影响压电陶瓷环的整体刚性,使综合弹性模量提高压电陶瓷环的整体刚性,进而增大综合弹性模量,导致谐振频率f增大,另一方面粘接层使得陶瓷环装配体整体厚度h增大,谐振频率降低;残胶层使得陶瓷环装配体整体内径r1增大,导致谐振频率f增大。
图17 中,非同轴装配的换能器TVR 曲线在27 kHz 处出现明显毛刺;图18 和图19 中,随着预紧力从5.7 N·m 增大到10.7 N·m,谐振频率增大约1.2 kHz,在谐振频率处的电导值也随之增大,换能器TVR 曲线明显后移。整体而言,仿真值与实测结果具有较好的一致性。由于真实材料内部不均匀,真实性能参数和仿真材料参数存在差异;有限元模型将换能器各个零件接触关系定义为理想面接触,而实际上各个零件之间微观上为局部点接触;实际测试中由于存在测量误差,测试值与真实值也存在差异。
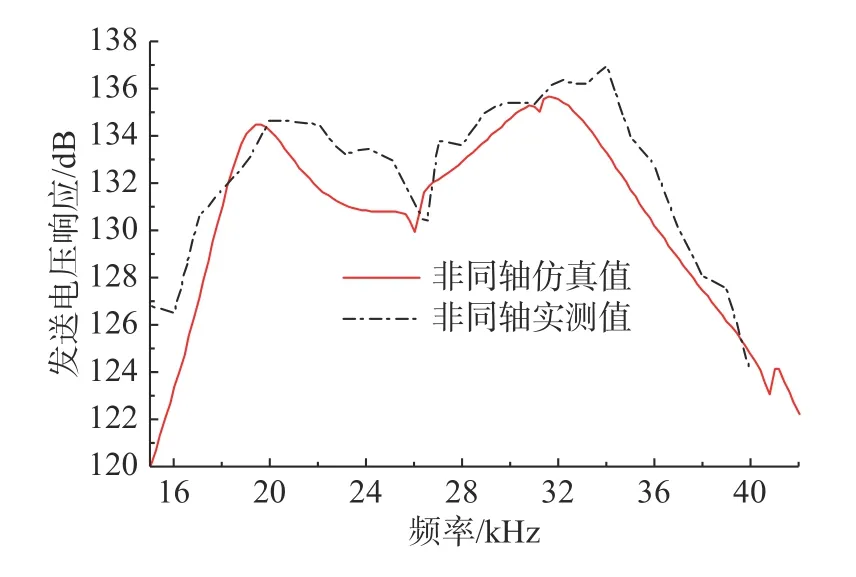
图17 非同轴装配方式下换能器TVR 仿真与实验对比Fig.17 Comparison of simulation and experimental data of TVR for non-coaxial assembly mode of transducer
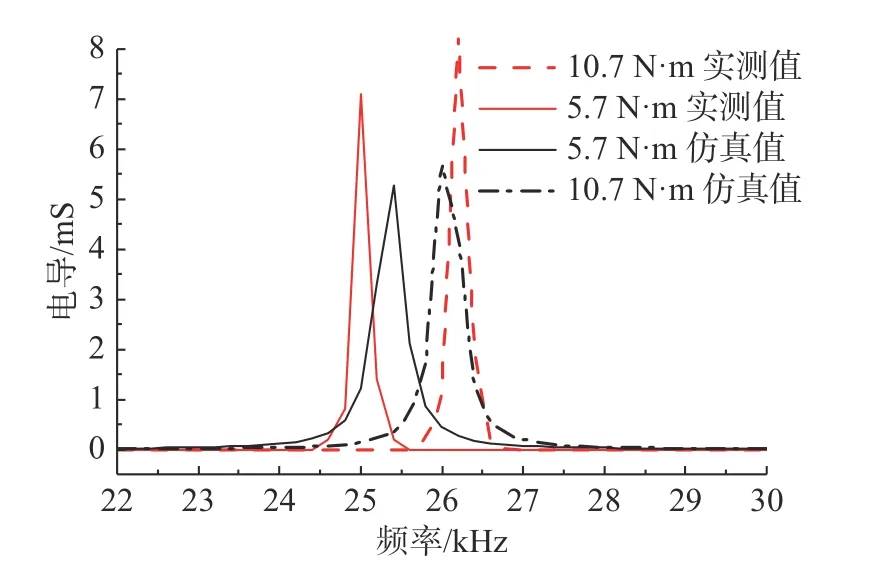
图18 2 种螺栓预紧力下电导随频率变化的仿真与实验数据对比Fig.18 Comparison of simulation and experimental data of conductivity variation with frequency under two bolt pre-tensioning force levels
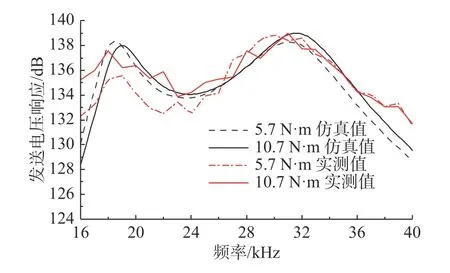
图19 2 种螺栓预紧力下TVR 仿真与实验对比Fig.19 Comparison of simulation and experimental data of TVR under two bolt pre-tensioning force levels
5 结论
采用有限元分析和试验验证的方法从2 个层面对匹配层换能器进行了较为深入的研究,通过研究可知:
1) 换能器涂胶粘接可以通过填补各零件端面间的微小空隙来提高压电陶瓷环的整体刚性,进而使得综合弹性模量增大,从而导致谐振频率增加;
2) 换能器谐振频率随着粘接层厚度增大而减小,随着残胶层厚度增大而增大;
3) 陶瓷环装配同轴度高的换能器TVR 曲线毛刺较少,曲线更加平坦,更适合传感应用;
4) 随着预紧力增大,换能器的1、2 阶谐振频率增幅较明显,发送电压响应曲线明显后移,生产过程中可以通过施加合适的预紧力使换能器调节至预期的工作频带内。
研究结果对换能器工艺研究具有指导意义,可有效提高换能器装配的合格率。
