一种基于安全多方计算的边缘学习协议*
2024-01-12李存华
孙 帆,雷 旭,李存华
(1.江苏海洋大学 计算机工程学院,江苏 连云港 222005; 2.东南大学 网络空间安全学院,江苏 南京 211189)
物联网环境下,高性能芯片的应用显著提高了边缘设备的计算能力,使得边缘设备能够通过边缘学习自主处理人脸识别、自动驾驶等场景下的计算任务。然而,边缘学习应用涉及多用户和设备之间的数据交互,不可避免地需要使用参与者的私人信息,所以隐私保护在边缘学习中成为一个不可忽视的问题。传统隐私保护计算方法计算量大,不适用于边缘学习环境。提出一种轻量级的隐私保护计算方法对于边缘学习至关重要。
近年来,关于边缘环境下的隐私保护计算逐渐成为研究热点。Domingo-Ferrer等[1]提出一种联合学习框架,为参与计算方提供保护以抵御网络中的拜占庭攻击和病毒。Gu等[2]通过改进的强化学习算法计算出特殊的纳什均衡,以实现边缘节点和终端用户的隐私保护数据传输。Han等[3]提出的PCFed是一种新的提升隐私保护与通信效率的联邦学习框架。Guo等[4]提出了一种训练填充模型来推断边缘节点的数据分布,并通过训练该模型在不侵犯用户数据隐私的前提下有效缓解训练数据不平衡所带来的问题。Du等[5]通过添加拉普拉斯机制保证隐私安全,并通过输出扰动和目标扰动算法实现差分隐私保护。Liu等[6]提出一种差分隐私上下文在线学习模型,用于移动边缘计算中的CHD诊断。Xiong等[7]提出一种智能三方博弈框架,以保证物联网移动边缘众测中的数据隐私。Li等[8]基于修改后的Okamoto-Uchiyama同态加密,为边缘增强的HCPSs(human cyber-physical systems)提出一种可验证的保护隐私学习预测模型,该模型为用户输出可验证的预测结果而不会泄露隐私。为避免社会物联网系统协同边缘计算的隐私泄露和安全危机,Zhang等[9]提出一种基于数据干扰法和对抗性训练观点的数据保护方法。
然而,上述研究大多是针对边缘—中心架构下的协同计算场景,对于边缘学习中涉及多个边缘设备间协同多方计算隐私保护的问题仍缺乏高效的解决方法。在边缘学习中,最主要的安全问题是边缘设备受尺寸和功耗所限,计算能力相对较弱。因此,传统隐私保护计算方法(如密码学方法、差分隐私和联邦学习)并不能直接用于这一场景。为了解决边缘学习环境中的安全计算问题,需要提出一种新的计算方法,该方法应该在提供隐私保护的前提下,减小边缘设备的计算开销。本文主要贡献总结如下。
(1) 提出了一种改进的安全多方计算边缘学习模型,给出了基于可信公共参数的多方协同计算流程。该流程可显著减少边缘设备对服务器的依赖,并通过协同边缘设备的计算资源,缓解边缘设备计算能力较弱的问题。
(2) 为避免边缘设备间复杂的加密计算,提出一种基于椭圆曲线的安全多方计算(elliptic curve-based secure multi-party computation,ECSMC)方法,该方法将边缘设备间的加密数据传递转化为基于服务器的椭圆曲线密钥传递,从而实现数据的密文计算。椭圆曲线有轻量级和高安全性的特点,可以满足边缘学习对隐私保护计算的需求。
1 系统模型
1.1 系统结构
如图1所示,本文考虑一个由中央信息站覆盖范围内的N个边缘节点组成的边缘学习系统。每个边缘节点都由边缘计算设备组成,这些设备通过梯度传递来训练同一模型,并为距离最近的用户提供计算服务。在这个系统中,用户提供数据并提出计算请求,而中央信息站则负责生成多方安全计算的共同参数,并将这些参数发送到系统中。这样,边缘节点和用户之间就可以直接进行安全的数据计算,而无需依赖中央信息站。所有参与计算的设备和用户都需要在中央信息站进行注册,否则它们就无法与其他设备或用户进行通信。这种注册流程的设置可以有效防止系统中的恶意用户。
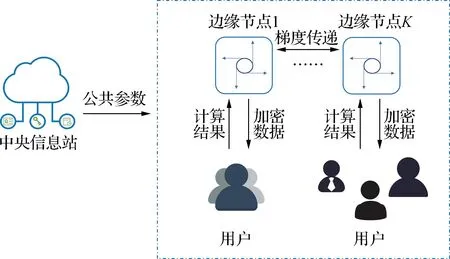
图1 安全多方计算系统结构Fig.1 Structure of secure multi-party comptation
1.2 计算流程
如图1所示,在边缘学习过程中,梯度是一种重要的中间参数,包含私人信息相对较少,因此可以使用ECC算法加密计算后再进行传输。然而,对于用户和边缘节点的数据来说,加密后传输可以保护计算双方的数据隐私,但多次加密解密操作会增加系统的时间消耗。此外,由于明文需要暴露给对方,这种方式也存在隐私泄露的风险。为此,本文提出一种基于安全多方计算算法的协议,使用椭圆曲线加密计算用户与边缘节点之间密文数据矩阵的内积。
在协议约定中,中央信息站首先会生成安全多方计算所需的参数。具体来说,中央信息站会选择一个大素数q,并使用ECC算法基于该素数生成一条椭圆曲线。同时,中央信息站会确定该椭圆曲线上的循环群G和生成元g。中央信息站生成完这些参数后,会将它们发送给已经注册的设备、用户和服务器等参与方,以供后续计算使用。单个用户与边缘计算节点之间的通信需用ECC,其流程如图2所示。用户选择一个数k作为其私钥,并与生成元g进行倍点计算,得到K作为其公钥,并发送给边缘节点。边缘节点在接收到用户公钥后,将私钥r与K相乘并加上明文M得到密文C,此时加密过程完成。边缘节点再计算自己的公钥R用于用户对密文解密,并将R和C发送给用户,边缘节点端的计算完成。用户使用C和R计算边缘节点发送的明文数据。

图2 ECC流程Fig.2 ECC process
上述的一般ECC流程只是单方数据传输,并未实现密文计算功能,所以本文在此基础上增加部分中间参数,构建ECC为基础的SMPC。以下为协议的具体计算流程,用户端需要进行两次计算,而边缘节点端需要进行一次计算。协议设当前边缘节点接入用户N个,记为矩阵U={U1,U2,…,UN},设U1用户参与计算的数据为XU1={x1,x2,…,xn},那么该边缘节点下各用户的数据表示为矩阵X={XU1,XU2,…,XUN}。对于边缘计算节点,协议将其参与计算的模型参数表示为矩阵AR={ar1,ar2,…,arm}。为避免明文计算,协议分别用随机数矩阵RD={RD1,RD2,…,RDN}和RS={rs1,rs2,…,rsm}混淆X和AR,其中RD集合中每项都是形如{rd1,rd2,…,rdn}的随机数矩阵,而n和m分别为用户和边缘节点数据向量的长度。在本协议中n和m值相同。矩阵Γ,θ和P用于保存协议中各用户加密计算协议的用户的中间参数,而矩阵P中各元素是椭圆曲线上被混淆的用户数据矩阵X′的映射。上述各用户中间参数的矩阵可表示为Γ={ΓU1,ΓU2,…,ΓUN},θ={θU1,θU2,…,θUN},P={PU1,PU2,…,PUN},X′={X′U1,X′U2,…,X′UN}。
为平衡安全性和计算效率,协议引入Γ和θ矩阵。它们的相关计算方法如下,以用户U1的计算为例,协议先从素数q的正整数域中抽取一个随机数,并将其表示为ρi。ΓU1是每个ρi,i={1,2,…,m}的椭圆曲线上的映射结果矩阵,即ΓU1矩阵中元素的计算方式为ρi·g。为提高用户数据的安全性,协议将矩阵ρ与P的乘积加上X′得到θ。用上述方法计算出各用户中间参数矩阵Γ,θ和RD,并发送给边缘节点。至此各用户端计算步骤第一步完成,开始边缘节点部分的计算。边缘节点使用Γ′和θ′计算自己的中间参数矩阵Γ′={Γ′U1,Γ′U2,…,Γ′UN}和θ′={θ′U1,θ′U2,…,θ′UN}。其中Γ′U1中各元素由Γi中的中各元素与a′j乘积,θ′U1计算矩阵θU1和矩阵AR的内积再减去Tji得到,而Tji是随机选取的群G中的元素。s2是用户随机数集合RD与边缘节点参数向量AR的内积,是需要减去的冗余项。Tj是每个Tji的和。至此,边缘节点端的计算过程完成,然后边缘节点将s2,RS,Γ′,θ′,Tj发送给用户。最后,用户通过计算TUi+Tj-s2得到X·AR。此时得到多方数据矩阵的内积计算结果。具体计算流程如算法1所示。
算法1隐私保护计算。
输入:多用户数据矩阵集合X={XU1,XU2,…,XUN}。
边缘节点参数AR={ar1,ar2,…,arm}。
输出:
用户端第一次计算:
1.选取随机数矩阵RD={RD1,RD2,…,RDN}。
2.计算矩阵X′=X+RD。
3.计算矩阵ΓUi=ρUi·g,i={1,2,…,N},其中ρUi是n个从q的整数集Zq选取的随机数,从而得到矩阵Γ={ΓU1,ΓU2,…,ΓUN}。
4.计算矩阵PUi=X′Ui·g,i={1,2,…,N},从而得到矩阵P={PU1,PU2,…,PUN}。
5.计算矩阵θUi=ρUi·PUi+X′Ui,i={1,2,…,N},从而得到矩阵θ={θU1,θU2,…,θUN}。
6.发送Γ,θ,RD给最近的边缘节点。
边缘节点端:
(1) 选取随机数矩阵RS={rs1,rs2,…,rsm}。
(2) 计算矩阵A′=AR+RS。

(4) 计算矩阵Γ′=AR·Γ。
(6) 计算s2=
(7) 发送s2,RS,Γ′,θ′给用户。
用户端第二次计算:
(1) 计算变量TUi=θ′Ui-
(2)
2 有效性分析和安全性分析
2.1 有效性分析
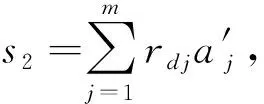
Tij+Tji=θ′i-x′iΓ′i+Tji=
a′iθi-Tji-xia′iΓi+Tji=
a′iρix′ig+a′ix′i-a′ix′iρig=a′ix′i,
(1)
TU1+Tj=
(2)
(AR+RS)(XU1+RD1)-s2-
(3)
式中Tij与Tji分别为用户端与边缘节点的中间参数。首先根据θ′i计算公式展开得到
2.2 安全性分析
下面对本文提出的协议进行安全性分析,以探讨该协议所能实现的数据保护功能。
(1) 保障边缘学习数据安全,各通信方无法知晓对方详细的输入数据,即保护双方输入数据的细节信息。用户与边缘节点之间以及边缘节点间的数据交互需经过ECC加密,能一定程度防止数据泄露。在协议开始时对双方数据加入随机数混淆,防止因密钥泄露而导致原数据被破解,其破解的复杂度与数据向量长度n相关。在这之后用户用ECC将X向量加密成θ向量,边缘节点无法从θ获取用户参数向量X。因为基于困难问题ECC算法具有较高的破解难度,256位密钥ECC其安全性与3 072位的RSA加密相当[10]。同样,用户也无法从接收到的参数中获取到边缘节点参数AR的细节信息。
(2) 保证边缘学习的模型安全,恶意用户无法通过多次计算获取关于模型参数的有效信息。边缘计算边缘节点的参数A在一开始就被经过随机数向量加密得到AR,且每次计算随机数都会改变。每次通过不同的AR计算结果表,用于用户对结果的查询。此时若根据计算结果反推边缘节点参数,此问题相当于求一个N元方程的解,且仅有一个方程,其解有无数种。因为每次产生的随机数向量不同,所以试图通过多次计算获取A值是不可能的。
3 实验分析
为了验证所提方法在边缘计算环境下的可行性和有效性,并且确保一定的安全性和可用性,本文进行了实验和安全性分析。设两组验证实验,一组是关于加密计算协议的计算时间,用于验证ECSMC相比其他密码学方法有更快的计算速度;另一组是关于本文提出的协议与当前边缘学习主流算法的训练时间和模型准确率的比较。
本实验设置了3台边缘节点,并模拟其使用用户数据进行边缘学习的过程,每个用户包含的数据量相同,且在计算完成后对边缘节点的模型参数进行聚合。实验设置在一台PC机上进行仿真,配置:CPU为I7-6700HQ;内存16 GiB;GPU为GTX 960M;使用python 3.7和pytorch 1.9.0+cu102库实现神经网络ResNet18和LeNet5。本实验使用的数据集为MNIST和CIFAR10,MNIST是一个10分类手写数字数据集,包含60 000个28×28像素的灰度图像样本,而CIFAR10是10分类彩色图像数据集,包含60 000个32×32像素的彩色图像样本。本实验神经网络的超参数设置为batch size=16,learning rate=0.001,选取的椭圆曲线为secp256k1,每个算法运行20次,记录相应的参数,求出它们的平均值,并进行比较。为更贴近边缘学习的应用场景,本文通过三个指标来比较算法:准确度、训练时间损失和损失值。
3.1 加密计算协议的计算时间
本协议使用ECC算法构建密文矩阵乘法计算方法,与目前使用较多的同态加密(HE)算法和密文计算方案进行比较,其安全性分析见文献[10]。在确保相同安全性的前提下,计算时间短的算法计算量较小,表明更适合边缘计算环境。两组相同长度的向量在这些算法上的计算时间见表1。从表中可以看出本文所提方案具有更短的计算时间,符合边缘计算应用场景。

表1 加密算法运行时间Table 1 Encryption algorithm runtime
3.2 协议在边缘学习的应用
为了验证ECSMC在边缘学习环境中的有效性,应用该方法于神经网络的图像识别与分类任务中,并以准确性和总计算时间为评价指标,评估其计算复杂度和性能表现。此外,损失函数的下降趋势也是训练效果的重要评价指标,也将其纳入分析范围。
(1) 算法的准确性。如表2所示,ECSMC应用于MNIST数据的准确度较差分隐私方法高约15%,比联邦学习低约5%。差分隐私的准确度低于其他方法,因为它在计算中加入太多噪音,导致训练后的模型准确度较低。联邦学习通过使用不同的设备来训练模型,解决训练阶段单一数据特征的问题,从而获得比单一节点更好的性能。在复杂的网络ResNet18和数据量大的数据集CIFAR10中,本文提出的协议准确率有所下降,这是因为随着网络参数和计算数据的增加,随机数噪声造成的精度下降经过神经网络中的损失函数计算愈发明显。若需要提升精度可降低随机数的数量。另外在网络参数更少的LeNet5中,识别准确率与原网络差距较小,随机数噪声的影响不明显,说明ECSMC在结构简单的网络中有较好的表现,而在边缘学习应用中保证一定的可用性提升计算速度更符合其低时延的需求。准确性的实验结果表明本协议适合网络简单、数据量少的边缘学习应用。
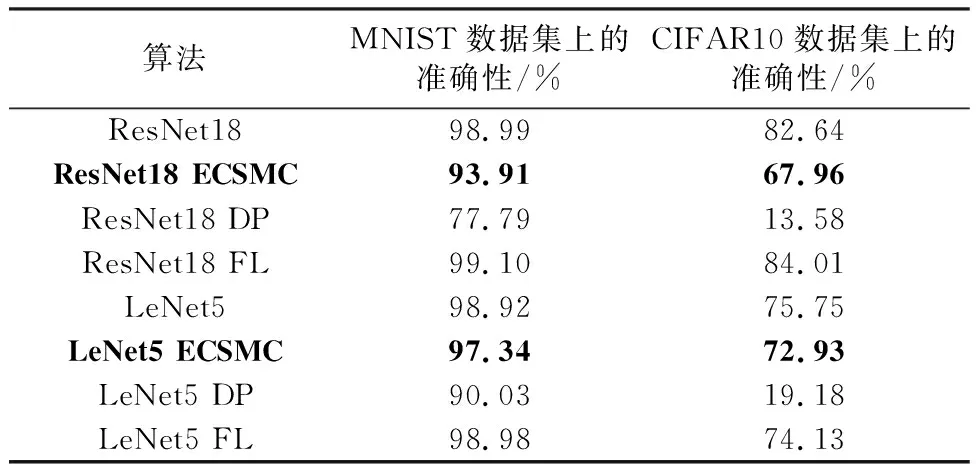
表2 不同算法的准确率Table 2 Accuracy of different algorithms
(2) 模型训练时间。如表3所示,ECSMC算法由于使用了ECC技术而具有最快的计算速度;联邦学习算法需要考虑到数据传输和设备间算力差异等因素,因此其训练时间通常最长;DP算法需要对整体数据进行随机数混淆,因此会增加训练时间。相比其他两种隐私计算算法,ECSMC所需训练时间更短,综合来看所需计算量和数据传输量更小,更适合于边缘学习环境。
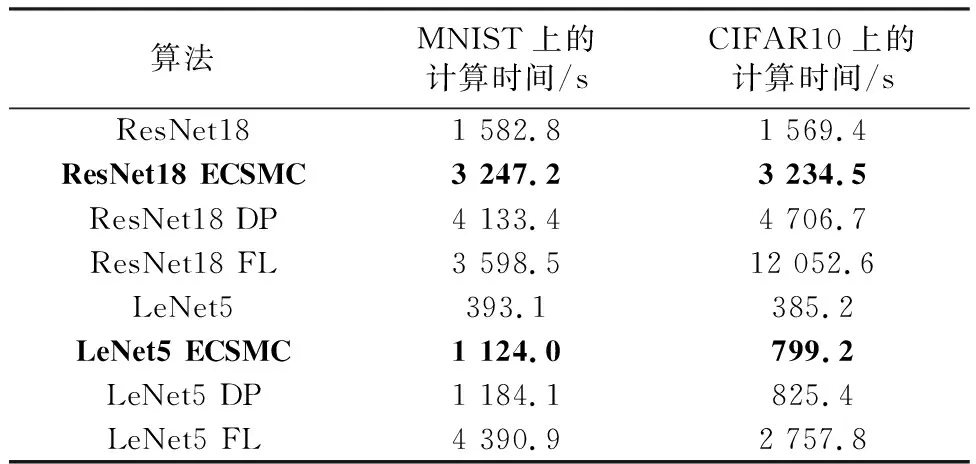
表3 不同算法的训练时间Table 3 Training time of different algorithms
(3) 损失值。本文对算法训练效果的分析还采用了损失值变化趋势这一重要指标。为减少复杂网络和大数据集对结果的影响,本实验使用一个简单的三层神经网络来进行MNIST数据集上的图像识别任务。该网络包含两个全连接层和一个带有激活函数的中间层。不同算法的损失值曲线如图3所示,这些算法包括普通算法(common)、DP算法和本文ECMSC。FL是多个common算法的组合,结果与common算法相似,所以没有在图中显示。普通算法是指不使用任何加密计算的算法。由图3可知,DP损失值下降曲线较平缓,由于在数据集中均匀加入高斯噪声,最终识别精度仅86.55%。本文方案在开始时损失值较大,与普通算法相比下降较快,与DP相比更贴近普通算法。然而,由于噪声的加入,本文方案的损失值波动较大,这在一定程度上影响最终的识别精度。在识别精度方面,普通算法、DP和本文提出的方法的精度分别为96.81%,86.55%和92.96%。普通算法、DP和本文方法的训练时间分别为96.15 s,223.38 s和131.38 s。
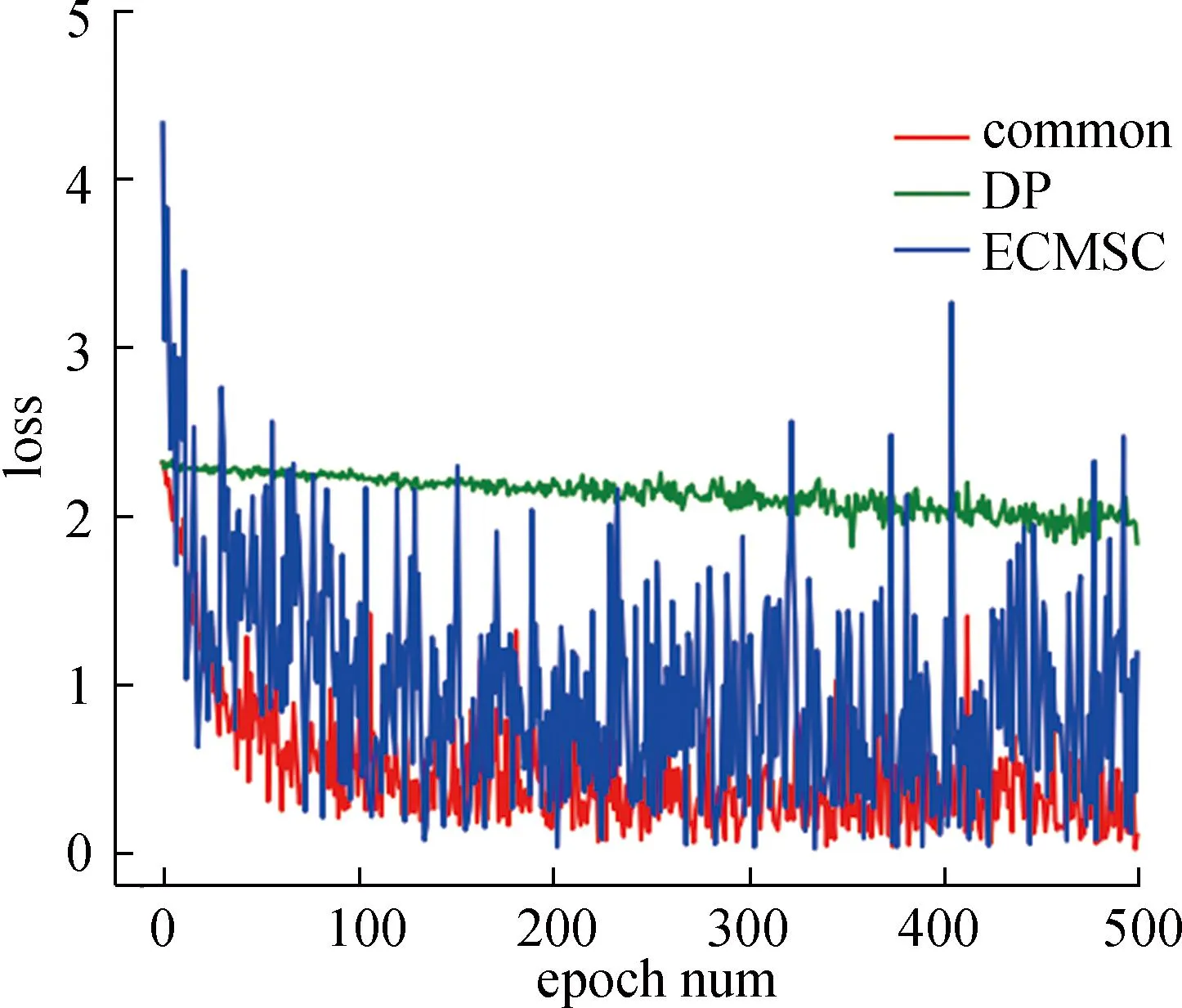
图3 不同算法的loss值对比Fig.3 Comparison of loss values of different algorithms
4 结语
本文提出了一种基于椭圆曲线的安全多方计算协议,并将其应用于边缘学习,以保障用户和边缘节点数据的隐私。该协议具有低计算复杂度和高安全性的特点,适用于边缘学习环境。本文的理论分析和实验结果表明,该协议在信息理论上是安全的,只要所选的素数足够大,椭圆曲线问题足够复杂,该协议就难以被破解。与差分隐私和联邦学习算法相比,ECSMC针对边缘学习场景进行优化,使用ECC技术降低计算复杂度并减少数据传输量,因此更适合边缘学习环境。在计算过程中,随机数噪声被添加到所涉及的参数中,数据被椭圆曲线加密以确保数据的隐私和安全。该协议不需要复杂的数据预处理,也没有联邦学习中因数据传输而产生的时间消耗,因此符合边缘学习隐私保护计算低时延的需求。
