基于计算流体力学的反渗透膜浓差极化研究*

2024-01-12蒋东升钱斌斌胡珊珊杨昊文方星星

江苏海洋大学学报(自然科学版) 2023年4期

蒋东升,钱斌斌,胡珊珊,刘岳,杨昊文,方星星

(安徽建筑大学机械与电气工程学院,安徽合肥 230009)

目前在世界人均淡水资源短缺的形势下,水资源污染日益严重,海水淡化成为解决此问题的重要方法之一。反渗透膜技术是海水淡化的关键技术之一。反渗透膜在压力下可以将原水中的离子、有机物等众多杂质拦截在水的高浓度一侧,而从低浓度侧产出高质量的纯水[1]。利用反渗透膜技术可以有效解决水资源不足问题,但反渗透膜长期使用难免会受到污染,并在膜表面形成边界层,之后产生浓差极化现象(CP),影响膜的净水性能。因此研究改善浓差极化对反渗透膜的污染防治以及提高产水率等性能指标有重要意义[2]。

国内外诸多学者对此展开了研究。张彤等[3]对正渗透膜内浓差极化对膜通量的影响进行研究,发现外浓差极化对膜通量影响较小,而内浓差极化与溶质进出支撑层的难易程度有关。刘建路等[4]以改善反渗透过程中浓差极化为出发点,讨论了可以除去海水中成垢离子的纳滤技术在预处理过程中的应用。Wiley等[5]利用有限元模拟软件CFX 4建立了二维的CFD模型,将壁面浓度与相邻流体动力学相结合,以预测浓差极化。Ahmad等[6]使用CFD软件Fluent v6集成了窄膜通道中浓差极化的CFD模拟。Wei等[7]建立了无量纲控制方程,该方程妥善解决了渗透通量与浓差极化之间的耦合;还通过解析解的闭合形式研究了RO过程中的浓差极化现象,并用新开发的模型描述了二维对流扩散溶质传输,预测了无隔板反渗透流道中的局部浓差极化和渗透通量。但二维上的反渗透膜CFD模拟缺乏对膜本身组件结构的考虑,忽略了膜内隔网等因素对浓差极化的影响。Baghdadi等[8]发现反渗透膜内随着温度升高渗透流量没有明显变化,而边界层厚度与温度的关系受到大分子嵌入聚合物基质影响。Karode等[9]曾使用三维模型对反渗透膜组件进行模拟分析,根据具体情况对反渗透膜模型做了合理的简化假设,采用层流模型对多种膜组件进行了CFD模拟,从而对膜组件中的流体流动和压降有了全面的认识。虽然该模型较为准确地模拟了膜内的流体流动,但采用层流模型较为不妥,不利于考虑湍流对膜内浓差极化的影响。为了消除这部分误差影响,本文通过软件对反渗透膜的浓差极化进行仿真模拟,建立了包含膜隔网的三维模型[10],较为全面地考虑到了反渗透膜内湍流、隔网等因素对浓差极化的影响,还研究了入口速度、雷诺数等参数对浓差极化的影响。

1 浓差极化

自利用反渗透技术解决水资源不足问题以来,膜污染和浓差极化问题一直制约着其推广和发展。如图1所示,浓差极化是被截留的溶质组分在膜入水侧表面不断积累,使得其浓度慢慢升高至与进水之间存在较大的浓度差,致使被截留的溶质反向向进水侧扩散,然后表面溶质浓度又逐渐减小。当进水侧溶质向膜面的流动速率与表面溶质向进水侧扩散的速率相等时,膜表面溶质会达到一种近平衡状态,这一稳定浓度区域就是边界层[11]。边界层与溶液之间离子交换过程中存在动量交换,分子层面的动量交换会导致分子在壁面附近扩散和混合,形成边界层并维持着;在力学方面会产生剪切应力与表面张力,这会导致边界层内的分子分布更加均匀和密集。这些动量交换会导致边界层内的流体产生湍流和涡旋,影响整个反渗透膜内流体流道的流动特性,溶液的入口速度会影响边界层的流速,但会达到平衡状态;动量交换一般会伴随着能量的转移,这里由于溶液与边界层温度一致导致温度不变;动量交换也会导致流体的阻力损失,由于黏性力的作用,这种阻力损失会影响整个流体流动过程的能量消耗[12]。边界层会使进水流向反渗透膜表面的流体阻力与局部渗透压增加,从而导致纯水透过通量下降,其厚度代表着膜内浓差极化的程度。

有学者认为浓差极化受溶质性质、具体膜的特性和具体溶液流体动力学影响,它也与轴向和横向流场有关联,而这些流场亦受到浓差极化的侧面影响[13]。反渗透膜进水的动量和质量输运的耦合,使得Navier-Stokes、连续性和对流扩散方程的联立解变得过于复杂耦合,因此理想化的浓差极化模型对于正确解释其机理研究非常重要,特别是那些侧重于阐明边界层扩散现象的基本机理的研究[14-15]。通过对边界层和溶质质量浓度进行数值模拟,再通过溶质的质量分数和边界层厚度来反映浓差极化现象。

2 浓差极化理论特性

2.1 边界层厚度评估

通过两种方法来评估浓差极化的边界层厚度,主要差别在于膜壁渗透的影响。第一种方法假设忽略了溶质的渗透,在膜通道稳定状态下,质量浓度分布是恒定的,假设停滞边界层中的总溶质输运为零。这意味着到膜的对流溶质传输等于从界面到本体溶液的扩散溶质通量[16-17]。其平衡由下式给出:

(1)

式中:ρ为溶质质量浓度,kg/m3;J1为水通量,L/(m2·h);Ds为溶质扩散系数,m2/s。

对式(1)积分可得

(2)

对式(2)再进行积分得到式(3),该方程提供了边界层厚度δ和膜表面溶质质量浓度ρw间的关系,

(3)

(4)

式中:δ为边界层厚度,m;ρw为膜表面溶质质量浓度,kg/m3。

在膜分离过程中,膜表面溶质质量浓度ρw高于进水溶液中溶质的质量浓度ρ,在膜附近的边界层中形成质量浓度差(ρw-ρ)。式(4)表示膜理论推导的边界层数值方法;式(5)假设边界层厚度δ近似等于离膜表面的距离,其中质量浓度值ρw足够接近溶质质量浓度ρ[18],

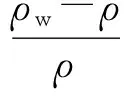
(5)

有学者[19]通过对二维通道反渗透脱盐过程中发生的浓差极化效应进行近似求解,得出

(6)

式中:h为通道高度的一半,m;Vw为壁渗透速度,m/s。

根据式(6)可以得出以下结论:在反渗透膜中,通过减小通道高度、增加入口速度(入口区域)或减小通道长度(以便停留在入口区域),都可以降低浓差极化,并提高脱盐效率。

第二种方法是寻找膜表面到有限质量边界(膜)层厚度δ之间的一维(横向)对流扩散质量平衡,并对其积分,得出浓差极化和渗透通量之间的关系[20]。结果为

(7)

式中:ρp为渗透溶质质量浓度,kg/m3。

2.2 雷诺数

雷诺数(Re)是控制流道内流体流型的关键参数,严重影响着反渗透膜内的浓差极化。本研究参考了膜组件不同参数下的雷诺数对流体流动的影响。雷诺数公式如下:

(8)

式中:ρl为流体的密度,kg/m3;μ为流体的黏度系数,Pa·s;v为流体的有效速度,m/s;D为特征长度,m。

特征长度D在此处为水力直径[21],定义为

(9)

式中:Vs和Vn分别为流道体积和隔网体积,m3;Ss和Sn分别为流道表面积和隔网表面积,m2。

流体的有效速度v定义为

(10)

式中:Q为体积流量,m3/s;A为有效面积,m2。

A=WHε。

(11)

式中:W为隔丝网间距,m;H为流道高度,m;ε为流道的孔隙率。其中孔隙率定义为

(12)

3 模型和方法

本文使用仿真软件进行数值模拟,以预测窄膜通道中不同类型条件下的浓差极化分布。在求解控制方程时,考虑了溶质质量分数等条件[22]。初步设置质量分数为5%的氯化钠(NaCl)溶液模拟进水,膜壁面上设置氯化钠溶液质量分数为35%以模拟膜的浓差极化。选用组分运输模型,在入口处扩散,重力与能量方程始终作用于整个模型,设置流体为不可压缩的牛顿流体。入口的湍流度受到来流的湍流度、流动状态、几何形状及流体性质等多种因素影响,被定义为脉动速度均方和与时均速度之比,经估算湍流度小于1%,为低湍流度[23]。为了使流体在雷诺应力上与真实湍流保持一致以及雷诺应力的约束条件可以被较好地满足,其黏性模型采用Realizablek—ε湍流模型[24]。数值求解器设置SIMPLE,采用稳态计算,保持默认的迭代收敛准则,连续性方程、速度等收敛标准为1×10-3,能量方程收敛精度默认为1×10-6,迭代次数为1 000。

3.1 物理模型

反渗透膜模型简化为渗透膜与支撑层之间的简单模型,选取部分区域用来模拟20 mm×5 mm×1 mm (L×W×H)反渗透膜区域内液体的流动和盐浓度。隔网每个单元半径为0.3 mm,长约2.24 mm,成圆柱形十字交叉排列,位于反渗透膜流道居中位置,隔网与入水方向成45°。康志雄[25]对隔网与入水方向之间夹角进行模拟分析,研究认为在45°时膜内流道中的流动死区大大减少,这有利于削弱浓差极化和膜污染现象,提高反渗透膜组件的渗透通量。而且在45°时反渗透膜壁面的剪切应力分布较好,压降最低即能耗最低,有利于提高反渗透膜的产水量。

3.2 边界条件

在模拟软件中,膜内环境温度设置在300 K,将反渗透膜面和隔网设置为不传热的壁面边界,即认为在膜面和隔网之间保持热力学平衡。入口和出口边界条件分别为速度入口和压力出口。初始入口速度为3 m/s,出口表压为0,回流湍流强度默认为5%,回流湍流黏度比默认为10。在对膜内流道主体流动的模拟计算中,由于反渗透膜的孔径非常小,其传质通量与流道内流体的流动速率相差数个数量级,因此忽略膜表面附近的轴向溶质对流,从而将复杂的输运问题简化为一维传质问题[26-27]。但对渗透流量进行计算时,则需要使用UDF对膜渗透关系进行设置。其中将渗透壁面设置为多孔介质,通过反渗透膜的渗透系数和渗透压差等系数得到渗透通量,自定义孔隙率和渗透率,修改黏性阻力和渗透率为UDF,这是由于黏性阻力为绝对渗透率的倒数[28]。为了准确地模拟边界层中盐含量的浓差极化现象,建立平行于膜表面的膨胀层网格应用于顶部和底部膜壁,以捕获陡峭的梯度,网格单元以四面体和棱柱体居多[29]。尽可能减小网格尺寸,靠近隔网部分更加密集紧凑,使网格数量尽可能更多,达到百万个单元以上,使用更细网格时无明显差异。

3.3 控制方程

假设流动是稳定的、不可压缩的,具有恒定的密度,并且是线性的,传输特性μ(黏度)和D(扩散性)可以是浓度的函数[30]。在质量守恒、动量守恒、能量守恒3大定律基础上,通过解流体力学3大方程得到对变量的描述。由于一般不考虑能量守恒方程,同时将溶液中溶质质量守恒方程考虑进来,采用Navier-Stokes方程来描述反渗透膜内的溶液流动[31-32],其质量守恒、动量守恒和溶质浓度守恒方程如下:

(13)

(14)

(15)

(16)

(17)

式中:u,v,w分别为流道内x,y,z3个方向的流动速度。

4 结果与讨论

4.1 云图结果

速度云图如图2所示。膜内温度为300 K,入口速度为3 m/s时,在模型中选取4个对称面,观察其中速度云图的变化情况。靠近膜壁面的流体速度较慢,靠近膜流道中心位置的流体速度较快,在膜隔网的上下两侧达到速度最大值4.87 m/s。在相同温度、不同入口速度时,膜内NaCl质量分数不同,其NaCl质量分数分布云图如图3所示。其中图3a的入口速度较低,图3b的入口速度较高,导致右侧流道内的NaCl质量分数不同,侧面反映了液体的入口速度改变对NaCl质量分数分布的影响情况。

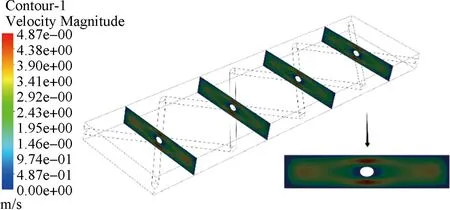
图2 速度云图Fig.2 Velocity contour

a 入口速度较低

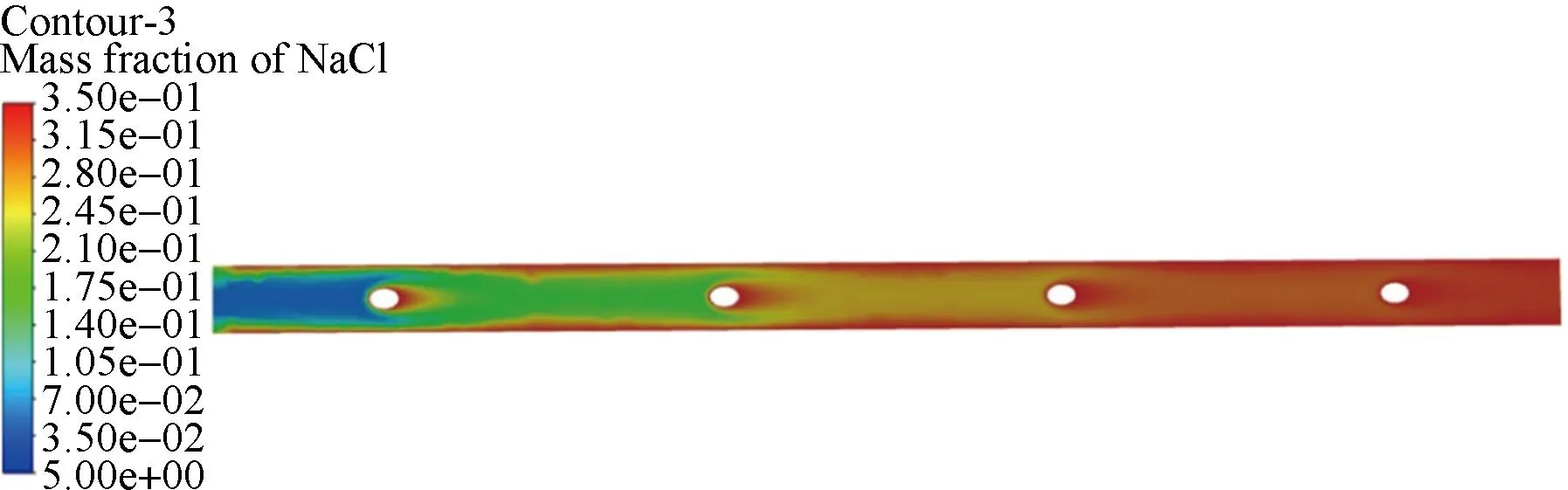
b 入口速度较高图3 NaCl质量分数云图对比Fig.3 Comparison of NaCl mass fraction clouds

4.2 入口速度对浓差极化的影响

本文中NaCl质量浓度分布包含了入口、出口和壁面,以面积加权平均下的NaCl质量分数来模拟NaCl质量浓度分布,边界层厚度来模拟浓差极化,NaCl质量分数与边界层厚度的关系如式(4)所示。在图4中,进入反渗透膜的液体速度在1～6 m/s之间,温度选取290,300,310 K。随着入口速度的增加,3种温度下的NaCl质量分数曲线较为接近,都先缓慢下降,后来加快下降,温度较高的NaCl质量分数也较高,标准差约为0.028 7。平均入口速度每增加1 m/s,NaCl质量分数都下降了约0.009 7%。

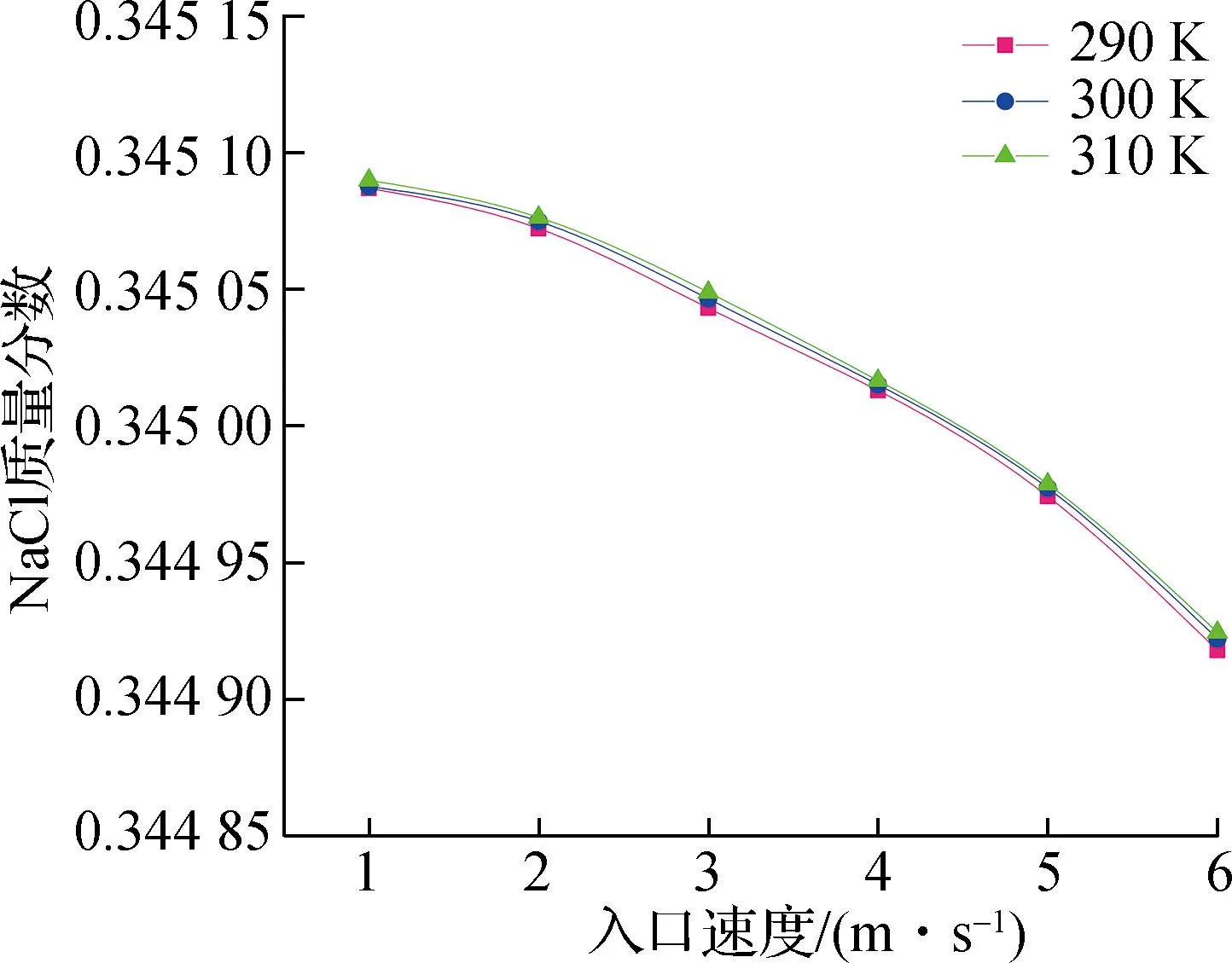
图4 NaCl质量分数随入口速度变化Fig.4 Variation of NaCl mass fraction with inlet velocity

边界层厚度随入口速度变化情况如图5所示。入口速度在1～2 m/s之间时,边界层厚度快速减小,入口速度在4～6 m/s之间时,边界层厚度缓慢减小,3种温度下的曲线较为接近且表现一致,温度高的边界层厚度小。这表明浓差极化现象随着入口速度的增加而减弱,可以解释为入口速度的增加促进了液体混合,增大了雷诺数,有利于冲刷浓差极化边界层,从而增强传质效果并减轻浓差极化作用。

图5 边界层厚度随入口速度变化Fig.5 Variation of boundary layer thickness with inlet velocity

同样是入口速度在1～6 m/s之间,温度选取290,300,310 K,反渗透膜内部NaCl的总质量变化情况如图6所示。随着入口速度的增加,3种温度下的NaCl总质量都随之降低,接近于线性关系,现象解释同上述一致。入口速度的增加减小了边界层厚度,边界层里的NaCl溶质进入流体中,速度越大,流量越大;NaCl流出反渗透膜,NaCl总质量降低。但NaCl总质量随着温度的升高而降低,在一定范围内表明温度的升高改善了浓差极化现象。

4.3 温度对浓差极化的影响

在图7中,当膜入口速度为3 m/s时,面积加权平均下的NaCl质量分数随着温度的升高而升高。温度在340～360 K时NaCl质量分数保持不变,边界层厚度随着温度的升高而增加。这解释为温度的升高改变了水通量和溶质扩散系数,溶液的黏度系数减小,流体更容易流动。流体在边界层内的速度增加,流动状况变得更为活跃,并且分子的热运动增大,分子间的距离变大,导致边界层扩散,随之变得更厚。边界层变厚会导致流体与壁面之间的摩擦力增大,阻碍流体在壁面附近的流动及壁面对流,促进壁面溶质盐沉积,减弱热对流的效率,这里膜与流体之间没有热对流不受影响。这些进而会导致渗透率和渗透通量降低,从而加重反渗透膜的浓差极化现象[32]。但温度升高也会增加溶质离子的热速率,即其在溶液中的扩散速度会增加,略微改善浓差极化。综合来说温度对浓差极化的影响是复杂的,并且受到多种因素的综合影响。

4.4 流体雷诺数对浓差极化的影响

雷诺数的大小反映着反渗透膜内流体的流动状态,影响着膜内的浓差极化。由式(8)计算得出雷诺数,雷诺数受到温度、入口速度、隔网的各种参数等因素的影响。温度影响着流体的密度和黏度系数,入口速度影响着流体的有效速度,隔网的间距、入水角度、厚度和构型等影响着水力直径D。

在图8中,3种温度下NaCl质量分数随着雷诺数升高而降低。当雷诺数为1 000～6 000时,NaCl质量分数下降缓慢,当雷诺数大于6 000时,NaCl质量分数加速下降,因为此时入口速度较大,温度较高,导致液体的黏度系数和密度降低,表明液体的黏度系数和密度会影响到传质效果和浓差极化。

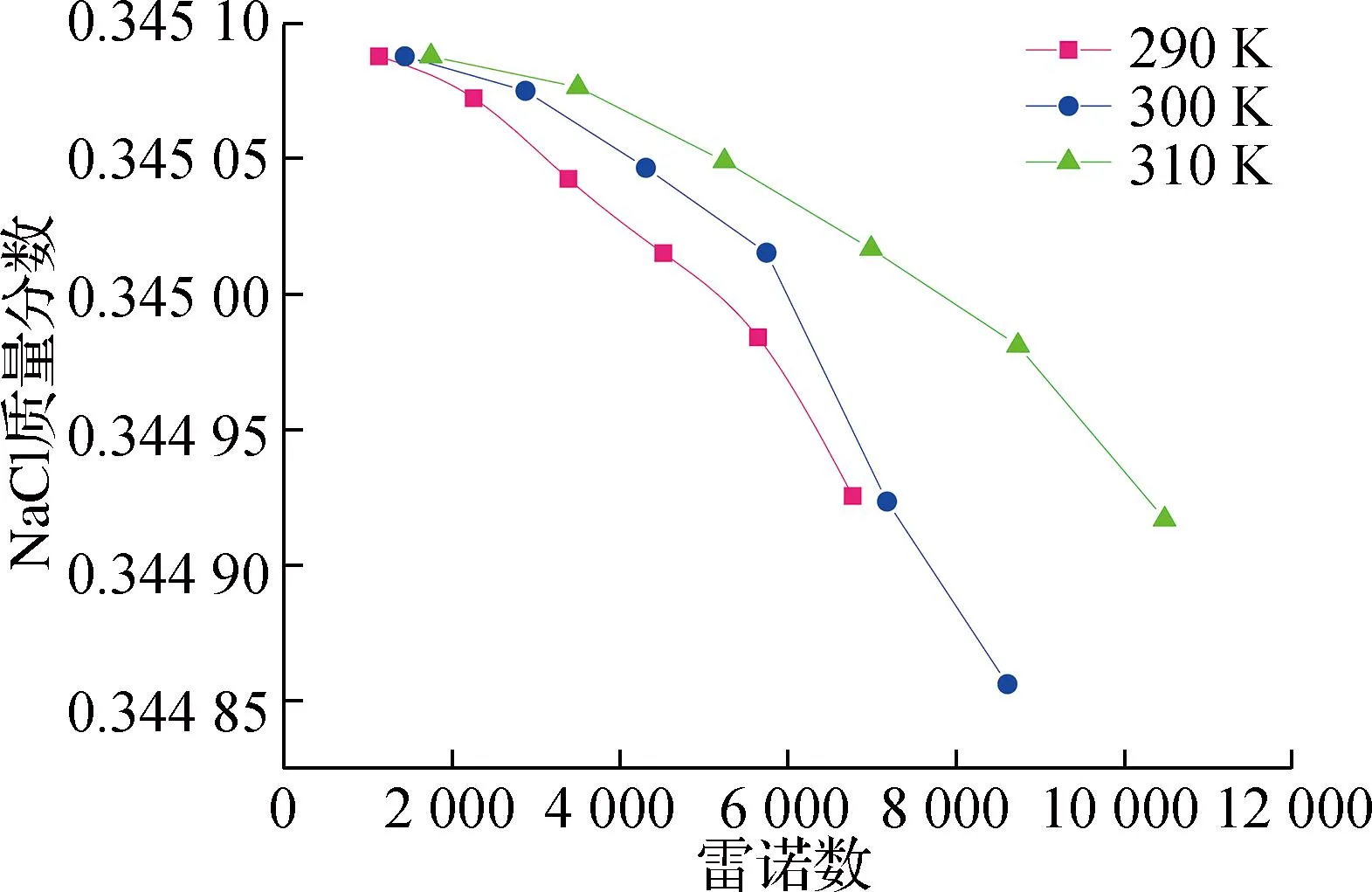
图8 NaCl质量分数随雷诺数变化Fig.8 Variation of NaCl mass fraction with Reynolds number

在图9中,边界层厚度随雷诺数变化,使用模型ExpDec1对散点图进行非线性拟合。方程为

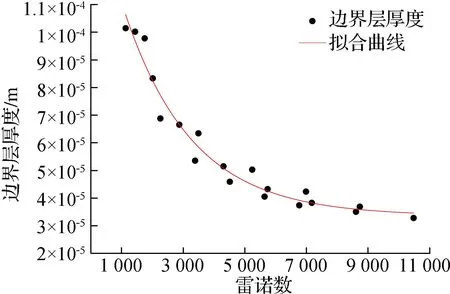
图9 边界层厚度随雷诺数变化Fig.9 Variation of boundary layer thickness with Reynolds number

y=A1×exp(-x/t1)+y0。

(18)

式中:y0=3.35×10-5±2.77×10-6,A1=1.21×10-4±9.65×10-6,t1=2 205.4±294.1。当雷诺数为1 000～6 000时,边界层厚度快速减小,当雷诺数大于6 000时,边界层厚度减小缓慢。这可解释为流体雷诺数的升高会伴随着流体有效速度的增加或流体黏度系数的降低;随着入口速度增加到一定值后,边界层厚度的减小速度也会放缓,而流体的黏度系数一般会受到温度和入口NaCl质量分数影响,温度升高和入口NaCl质量分数降低都会导致流体的黏度系数降低,而温度升高会导致NaCl总质量降低和质量分数升高,从而导致边界层厚度缓慢减小。

4.5 入口质量分数对浓差极化的影响

入口NaCl质量分数的降低同样会导致边界层厚度缓慢减小,如图10所示。当入口NaCl质量分数在0～0.01之间时,边界层厚度快速增加;当入口NaCl质量分数大于0.01时,边界层厚度缓慢增加。原因和上述解释一致,是入口NaCl质量分数引起了雷诺数的变化,但由于边界层上的NaCl晶体不断溶解入溶液里,所以后来边界层厚度增加缓慢。