基于时空信息的区域内光伏电站功率预测
2024-01-12刘运超杨宁崔承刚岑俊
刘运超, 杨宁, 崔承刚, 岑俊
(上海电力大学自动化工程学院, 上海 200090)
光伏发电作为一种清洁能源的发电方式,对于构建清洁低碳安全高效的能源体系、实现“碳达峰、碳中和”目标至关重要[1]。国家第十四个五年规划表明2030年太阳能发电、风电总装机容量达到12亿千瓦以上[2]。光伏发电是利用太阳能的重要方式,但受天气变化的影响,具有很强的波动性和间歇性,其大规模并网威胁着电网的稳定性和安全性[3]。因此,提高光伏发电功率预测的准确度对于电网的统筹调度具有重大意义[4]。
目前,中外学者已经对光伏功率预测做了大量的工作。预测方法按照实现方法主要分为两类:直接预测和间接预测[5]。直接预测是以历史功率和气象统计信息对光伏未来出力进行预测[6]。间接预测是根据气象信息数据建立特定的物理模型预测光伏的出力[7]。这些方法虽然对单个电站的预测精度能够达到要求,但是,随着光伏发电装机容量的提高,一定区域内出现多个电站,各个电站的发电功率受地形、组件安装倾角和云的移动等因素的影响,电站之间存在空间和时间上的相关性[8]。文献[9]提出了一种基于时空信息组合的分布式光伏功率预测方法,首先利用XGBoost-LSTM模型提取时序特征对目标光伏电站进行预测,然后利用LSSVM算法和相似电站建立空间预测模型。文献[10]提出了一种基于GCN的分布式光伏功率预测方法,并结合注意力机制赋予历史数据不同的权重来提高预测精度。文献[11]提出了一种用于太阳辐照度预测的方法,该方法采用图卷积神经网络挖掘分布式光伏电站的时空相关性。文献[12]提出了一种短期的光伏功率预测的图模型方法,建立了由谱图卷积和层次输出方式组成的模型。上述研究取得一定成果,但仍有一些问题:①未充分挖掘区域分布式电站空间和时间上的相关性;②预测时仅考虑单个电站的功率预测,未考虑对区域内电站总的输出功率进行预测。
现结合相似日聚类、信息熵分析、动态图卷积网络和长短期记忆网络(long short-term memory network, LSTM)提出一种基于时空信息的区域内光伏电站总功率预测的方法。首先,基于K-means进行相似日聚类,将数据划分为晴天、多云、阴天3种类型。其次,通过标准化互信息(normalized mutual information,NMI)分析空间上的相关性,并利用动态图卷积提取空间特征。然后,基于LSTM网络提取时间上的相关性,从而进行区域内光伏功率预测。最后,利用澳大利亚爱丽丝泉的光伏电站运行数据进行算例分析。
1 基于K-means算法的相似日聚类
1.1 区域内光伏电站总功率的预测
对于区域内光伏电站总功率的预测可采用先对单电站的发电功率预测,再将所有电站的预测结果累加得到总的预测功率的预测方法。但其需要分析每一个电站的特征,并为每一个电站构建一个功率预测模型,工作量较大。另外,每一个模型都有一个预测误差,将所有电站的功率预测相加也就意味着总的预测功率会有多个误差源。因此,采用先将区域内所有电站功率累加,再对总功率进行预测的方法。该方法所需功率预测模型较少,且预测误差源较少。同时,在相似日聚类时直接根据区域内电站总功率进行聚类。
1.2 相似日聚类
在不同的天气情况下,光伏电站的日发电曲线的差异较为明显,因此可对不同的天气类型进行聚类、训练相应的网络模型参数来提高预测模型的精度[13]。K-means算法是一种基于欧式距离的聚类算法,将样本数据聚类为k个簇,样本距离中心值越近,相似度越大[14]。本文研究通过K-means算法将光伏电站的日发电数据划分为晴天、多云和阴天三种天气类型,日发电曲线的特征量可表示为
Mi=[mmax,i,mmean,i,mkurt,i,mskew,i,mstd,i]
(1)
式(1)中:mmax,i、mmean,i、mkurt,i、mskew,i、mstd,i分别为第i天电站总功率最大值、平均值、峰度、偏度和标准差。
采用K-means算法聚类得到的3种类型的功率曲线簇如图1所示,晴天下的功率曲线簇的幅值较高,多云下的功率曲线簇的幅值降低,功率波动变大,阴天下的功率曲线簇的波动最大。在下文中将会对不同的天气类型下的数据集建立相应的训练集和预测模型来提高预测的精度[13,15]。
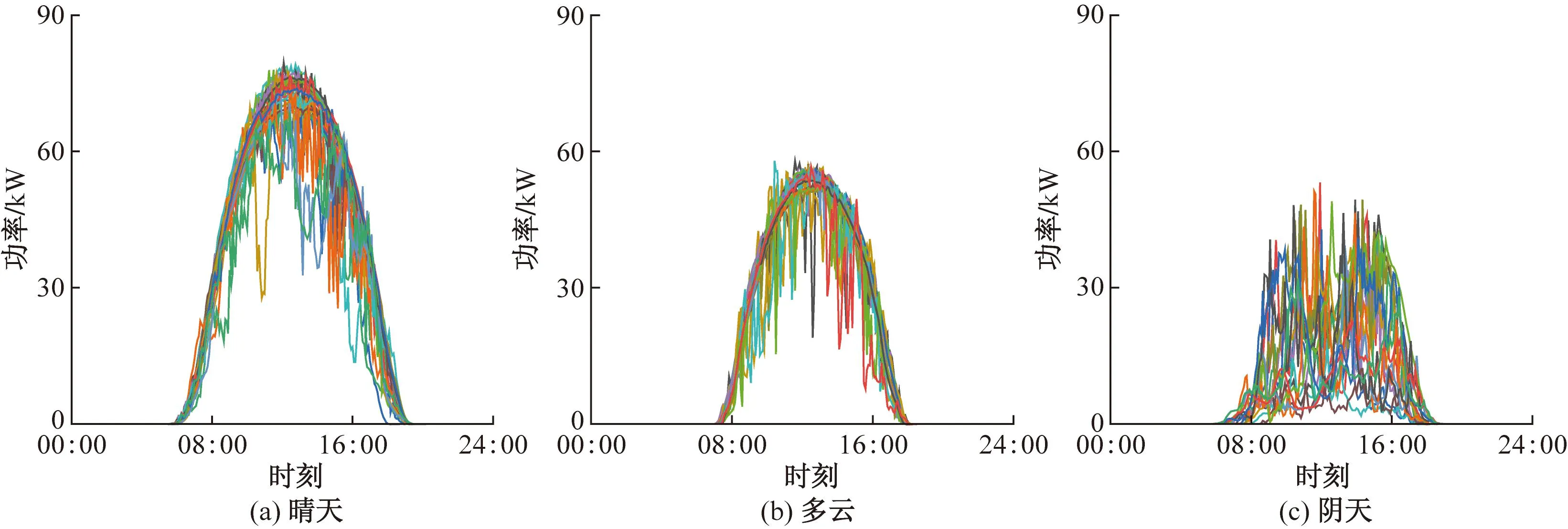
图1 3种天气类型的光伏发电功率曲线簇Fig.1 Power curve cluster of photovoltaic generation in three weather types
2 基于GCN-LSTM算法的区域内光伏发电功率预测
2.1 基于GCN的空间特征提取
区域内光伏电站在空间上的拓扑结构可采用一个无向的加权图G=(V,E)来描述,其中V=(v1,v2,…,vn)是区域内电站节点的集合,每个电站对应图G中的一个节点;E是加权边的集合。各节点间的权值关系可用邻接矩阵A∈Rn×n表示,其中n为维度。A中的元素aij或aji表示节点vi和vj间的相关信息。
通过区域内各电站的历史特征信息提取时空信息可进行电站总功率的预测,然而,这种方法在提取特征信息时仅提取了各电站间的时空相关信息,与电站总功率无关,致使缺少重要的特征,即电站总功率与各电站功率的时空相关信息特征。因此,构建一个假想电站节点作为电站总功率节点,其功率为区域内所有电站功率之和,则图网络结构的节点数变为n+1个,邻接矩阵的阶数变为n+1阶,即A∈R(n+1)×(n+1)。图网络结构变化如图2所示。
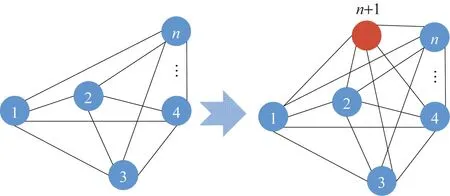
n+1节点为电站总功率节点图2 图网络结构变化Fig.2 Graph changes in network structure
2.1.1 邻近电站的动态空间相关性
光伏发电功率受地形、组件安装倾角和云的移动等因素的影响,邻近电站的出力在空间上具有相似的变化趋势。如图3所示,某地12个光伏电站的日出力在数值上有一定的差距,但在变化趋势上有很强的相似性。为了挖掘空间维度中的特征信息,采用NMI来计算邻接矩阵中各元素的值。NMI是信息论中一种对信息的衡量方法,通过信息熵来描述变量的不确定性,随机变量的信息熵如式(2)所示,得到信息熵后,NMI可表示为式(3),其值范围为[0,1]。该值越大,两个随机变量之间的相关性越强。
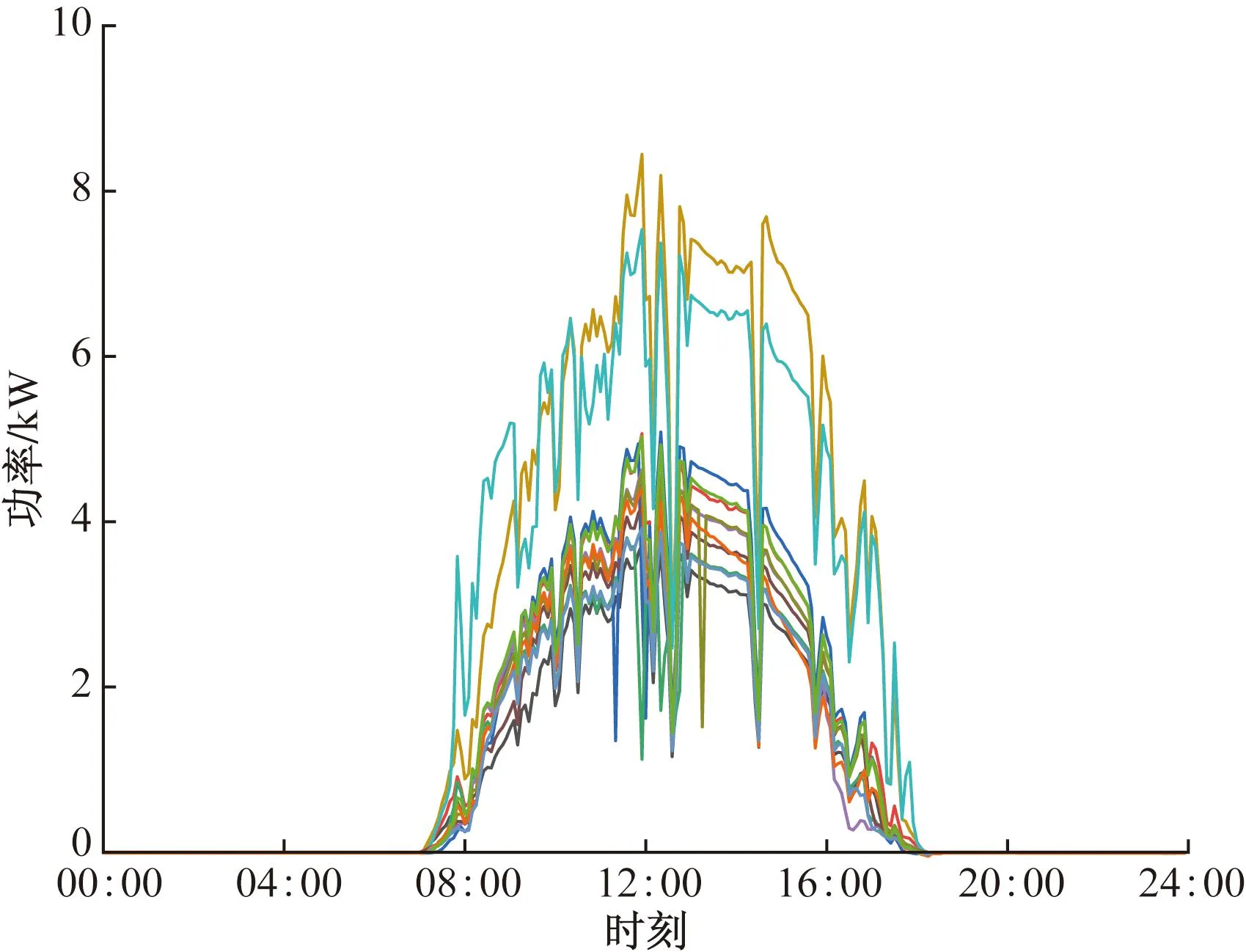
图3 区域内12个电站的日发电曲线Fig.3 Daily generation curve of 12 plants in the region
(2)
(3)
式中:X、Y为两个时间序列变量;pr(·)为概率函数。
传统上图卷积网络采用一个静态的图网络结构来提取空间特征,邻近两个电站之间的NMI值如图4所示。图4中可以说明两个邻近的电站之间的光伏输出功率在空间维度上具有很强的相关性。而且,两个电站的NMI值是变化的,说明空间相关性不是静态的,而是时变的。然而,传统的图卷积采用静态图网络结构,忽视了时变的相关性对预测精度的影响。因此,为提高功率预测的精度,图卷积网络采用动态的图网络结构。动态相关性在数学上用时变的邻接矩阵At来表示,在T时刻及其后4个时刻的空间相关矩阵的变化如图5所示。
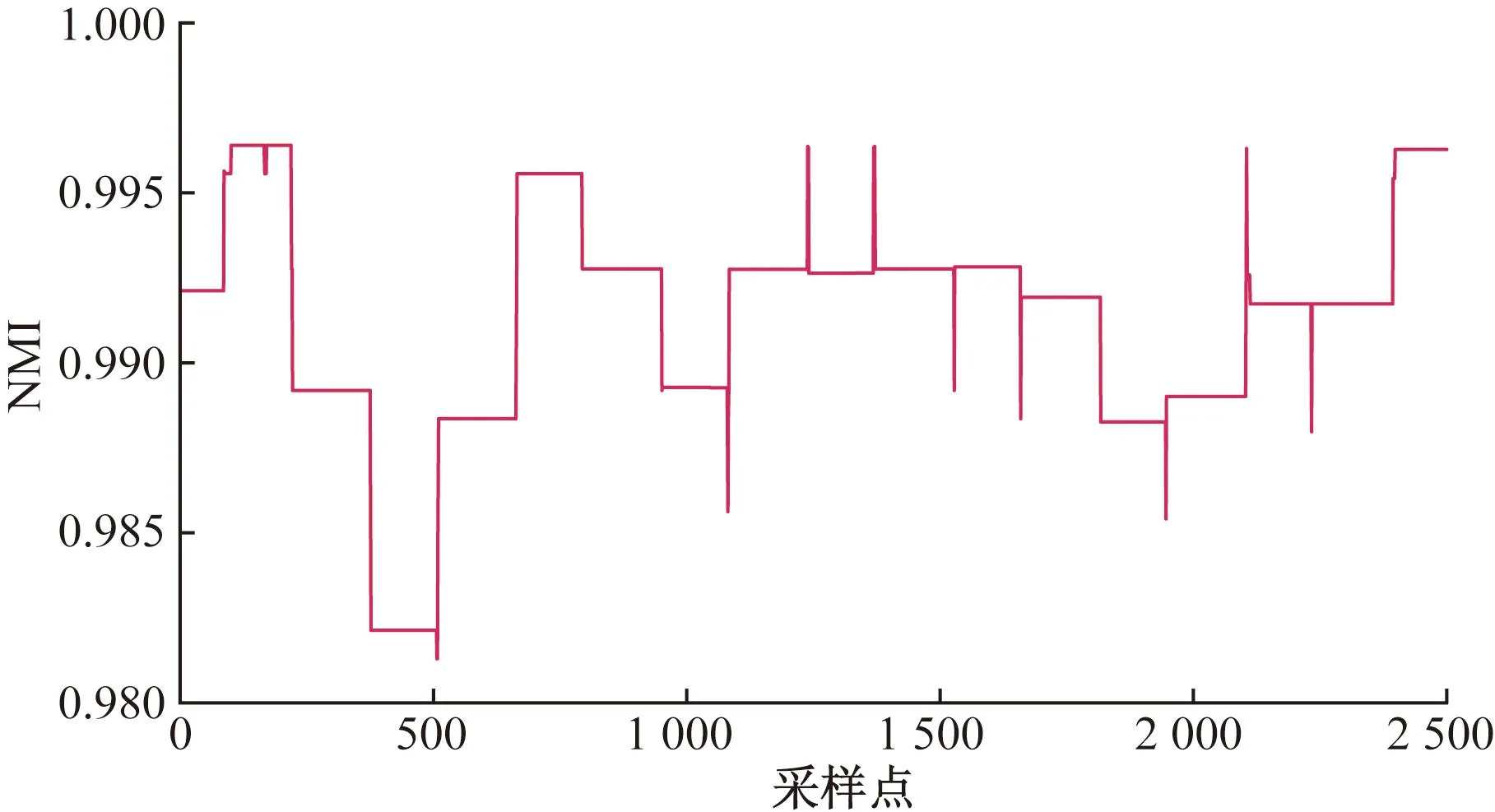
图4 两个邻近电站的NMI值Fig.4 NMI value of two adjacent plants
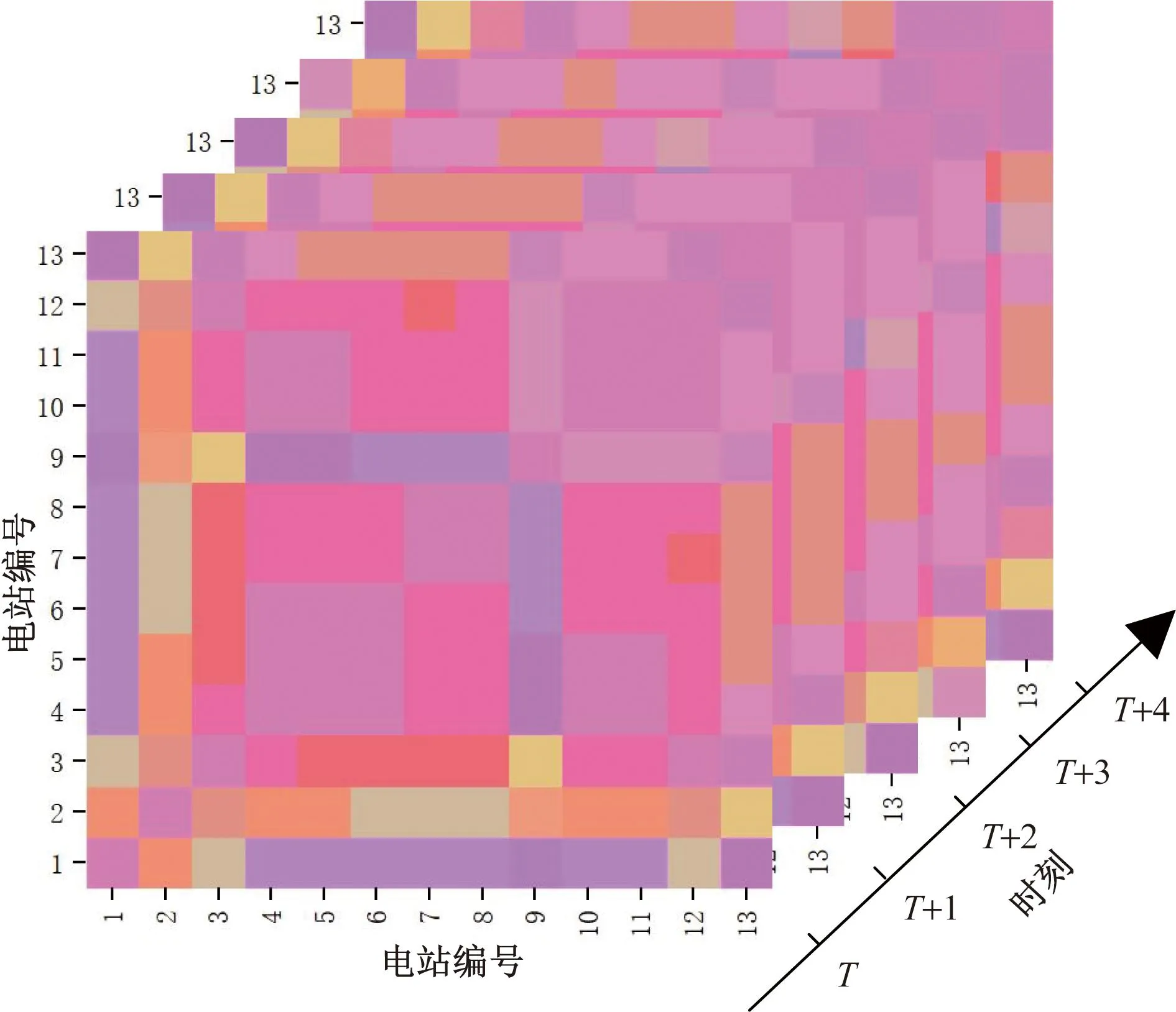
图5 动态相关矩阵Fig.5 Dynamic correlation matrix
2.1.2 谱图卷积
图卷积网络的处理对象是图数据,可从输入数据中挖掘数据的空间相关性,通过GCN提取空间特征一般由多层图卷积组成,它类似于一个感知器,有一个由光谱卷积驱动的邻域聚合步骤[16]。在数学上,一个多层的GCN通过分层规则更新所有节点特征,其传播规则可表示为
(4)
(5)

2.2 基于LSTM网络的时间序列预测
LSTM网络是一种时间循环神经网络,能有效地传递长时间序列中的信息且不会导致有用信息被遗忘[17]。光伏发电数据是时间序列,在时间上具有一定的联系,而GCN难以捕捉这种联系和区别。为了挖掘光伏出力在时间维度中的特征信息,采用LSTM网络对时间序列进行分析。LSTM网络的运算过程中信息的传播规则可表示为
ft=σ(Wf[ht-1,xt]+bf)
(6)
it=σ(Wi[ht-1,xt]+bi)
(7)
Ct=ft⊙Ct-1+it⊙tanh(Wc[ht-1,xt]+bc)
(8)
ot=σ(Wo[ht-1,xt]+bo)
(9)
ht=ot⊙tanh(Ct)
(10)
式中:xt为t时刻输入值;ht-1、ht为t-1、t时刻输出值;ft为遗忘门输出值;it为输入门输出值;Ct-1、Ct为t-1、t时刻神经元状态;ot为输出门输出值;Wf、Wi、Wc、Wo为网络层权重;bf、bi、bc、bo为网络层偏置;⊙为哈达玛积运算符。
2.3 基于GCN-LSTM算法的电站功率预测模型构建
对于区域内光伏电站,在空间上与邻近电站的出力有关,在时间上与历史时刻的功率有关。在预测区域内光伏电站总功率时,将电站抽象为图网络结构模型,n个电站抽象为n+1节点。第n+1个电站是一个假想电站,其输出功率为区域内所有电站功率之和。算法的预测模型的输入和输出可表示为
(11)
Xt,i=[xt-H+1,i,xt-H+2,i,…,xt,i]
(12)
(13)
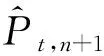
预测模型的输入、输出关系可表示为
(14)
式(14)中:f(·)为GCN-LSTM算法的模型。
区域内电站之间时空信息的提取如图6所示。在T时刻,通过NMI(XT,1,XT,2)得到电站1和电站2在空间相关性,即图5中T时刻邻接矩阵中电站1和电站2对应的两个元素。区域内所有电站间的相关性构成阶数为n+1的邻接矩阵,即可表示图5中T时刻的邻接矩阵。两个电站在时间上以宽度为H的窗口滑动来挖掘时间上的特征。
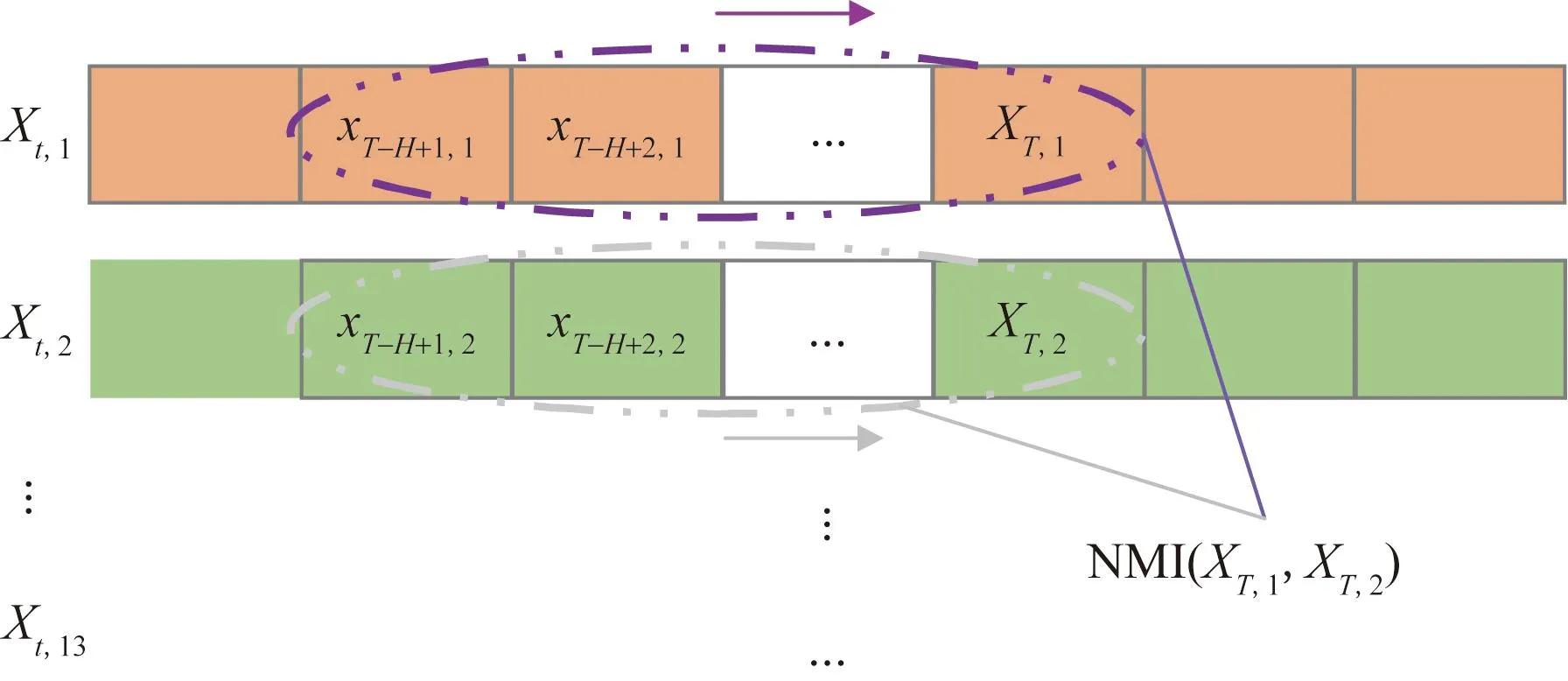
图6 区域内电站时空信息特征的提取Fig.6 Extraction of spatiotemporal features of plants
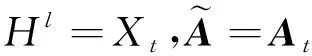
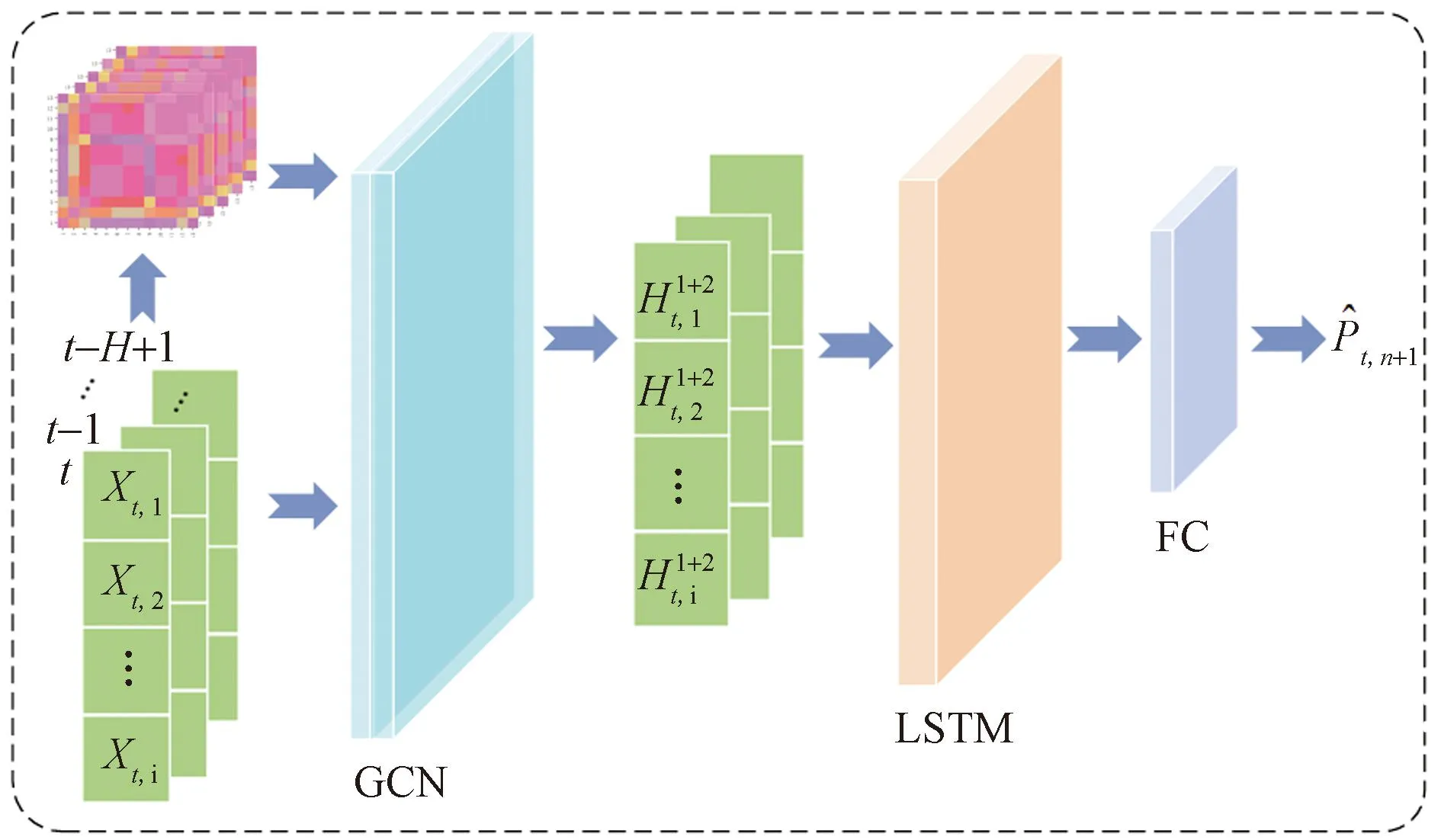
图7 预测网络结构Fig.7 Predictive network structure
3 算例分析
3.1 数据处理
以澳大利亚爱丽丝泉12个光伏电站在2021年5月1日-2022年4月30日的光伏出力数据为实验数据,采样间隔为5 min。由于设备异常运行或故障检修,存在部分数据缺失的现象,数据异常或缺失单个数据则采用前一时刻和后一刻数据的平均值进行替代,缺失严重的部分则将当日数据剔除。在训练前对处理好的数据进行归一化。
3.2 预测结果评价指标
为评估预测结果,选取平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为预测效果的评价指标[19],计算公式可表示为
(15)
(16)
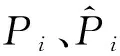
3.3 预测结果分析
3.3.1 不同天气类型下的预测结果
为验证所提预测方法的有效性,利用1.2节聚类得到的晴天、多云和阴天条件下的三份数据集分别建立相应的预测模型,预测算法采用所提方法、CNN-LSTM、GCN、支持向量回归(support vector regression,SVR)。4种预测方法在3种天气类型下的预测结果如图8所示,可看出在3种天气类型下,4种预测结果都能趋近电站功率的真实值,但在晴天下的功率预测曲线比在多云和阴天下的趋近度更高,这是因为多云和阴天下存在较大的功率波动。4种预测方法在3种天气类型下的预测误差评价指标如表1所示,GCN-LSTM算法在晴天、多云和阴天下的MAPE、RMSE分别为1.51%、2.22%、2.00%、3.38%、2.90%和5.04%。由于功率曲线波动变大的原因,天气条件越恶劣,预测误差越大。但是相较于CNN-LSTM、GCN和SVR算法,GCN-LSTM算法的预测误差较低。总的来说,GCN-LSTM算法与电站功率的真实值拟合度更高,预测精度更高。
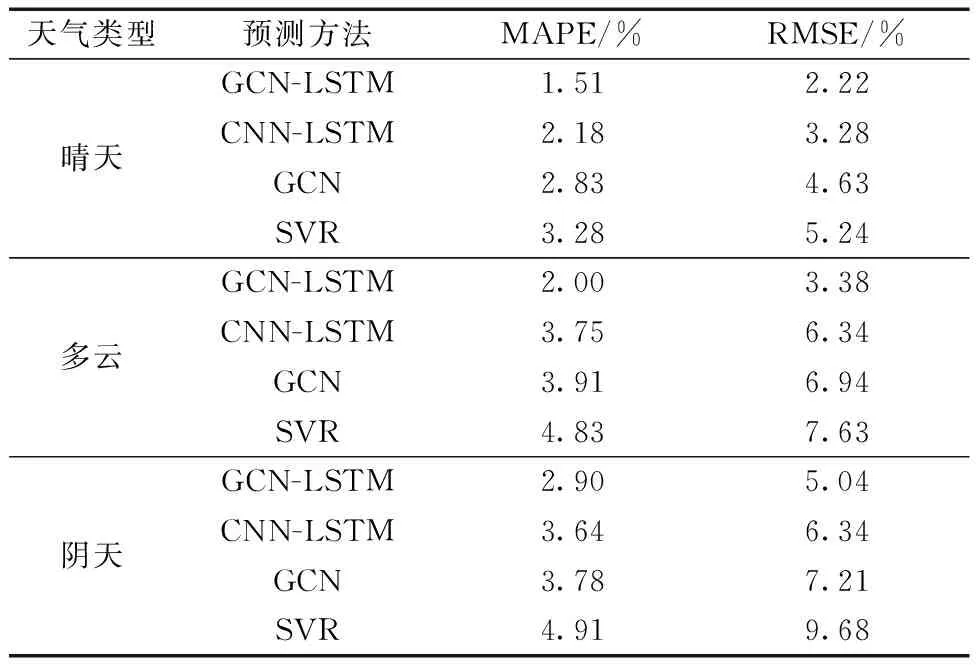
表1 不同预测方法在3种天气类型下的预测指标Table 1 Prediction indexes of different prediction methods under three weather types
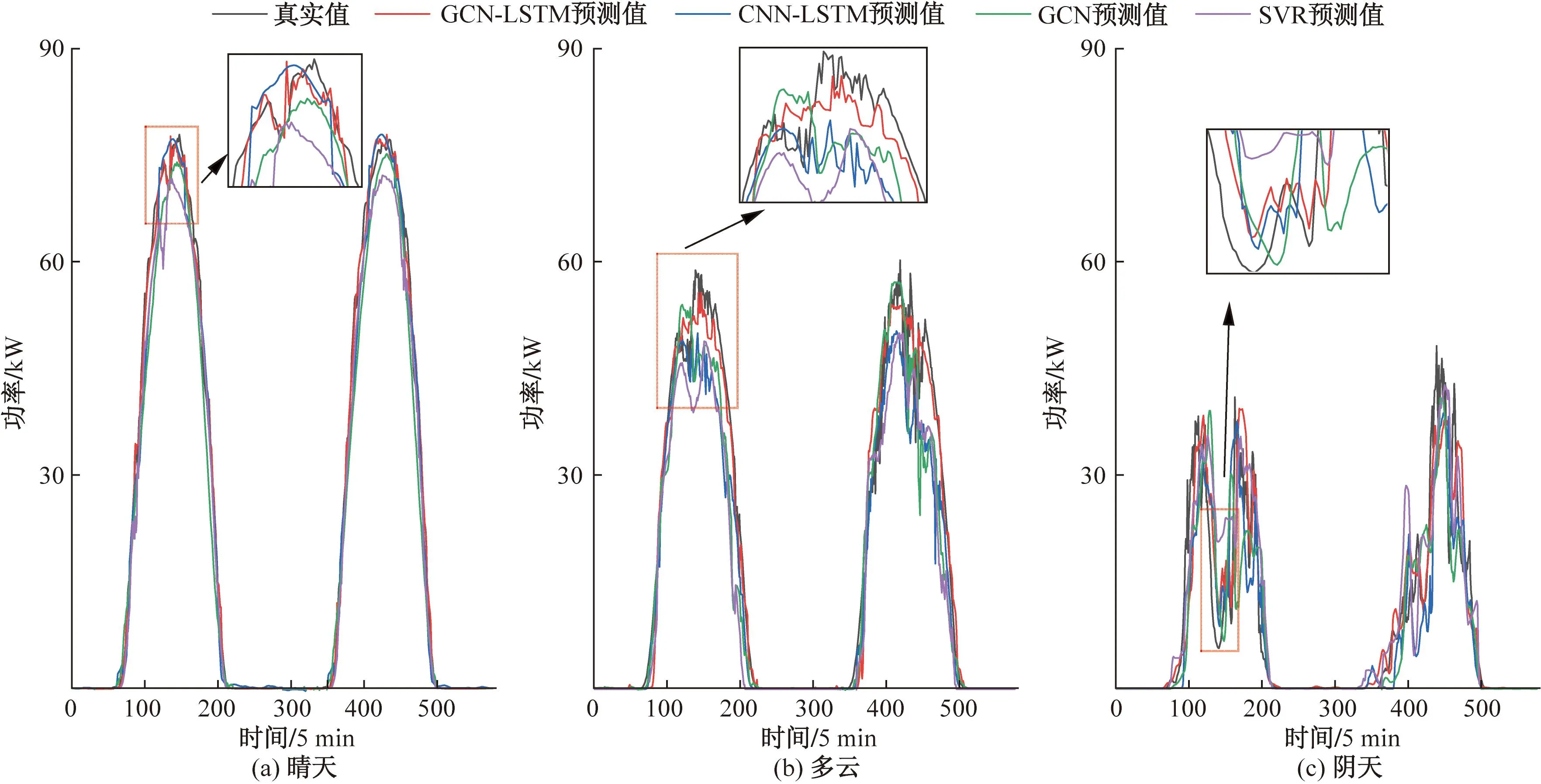
图8 4种预测方法在3种天气类型下的预测结果Fig.8 Prediction results of four prediction approaches under three weather types
3.3.2 动态图网络结构对预测结果的影响
由于邻近电站的NMI值是不断变化的,为进一步挖掘电站间的空间相关性,采用了一个动态图网络结构。为验证动态图网络结构对于功率预测的影响,在晴天条件下,与静态图网络结构进行对比,评价指标如表2所示,预测结果如图9所示,可得动态图网络的预测精度更高,这主要是因为动态图网络结构对邻近电站空间相关信息的挖掘更加充分,对其功率趋势变化的拟合度更高。

表2 动、静态图网络的预测指标Table 2 Prediction index of dynamic and static graph network

图9 动、静态图网络预测结果比较Fig.9 Comparison of dynamic and static network prediction results
3.3.3 假想电站对预测结果的影响
为了挖掘区域内总功率与区域内电站的时空相关信息,定义一个假想电站。为验证假想电站对预测结果的影响,在多云条件下,预测结果如图10所示,可得在加入假想电站的情况下功率预测精度更高。而且,未加入假想电站的预测结果与电站功率真实值的拟合度大大降低,这是因为在未加入假想电站的条件下失去了挖掘空间相关信息的能力。
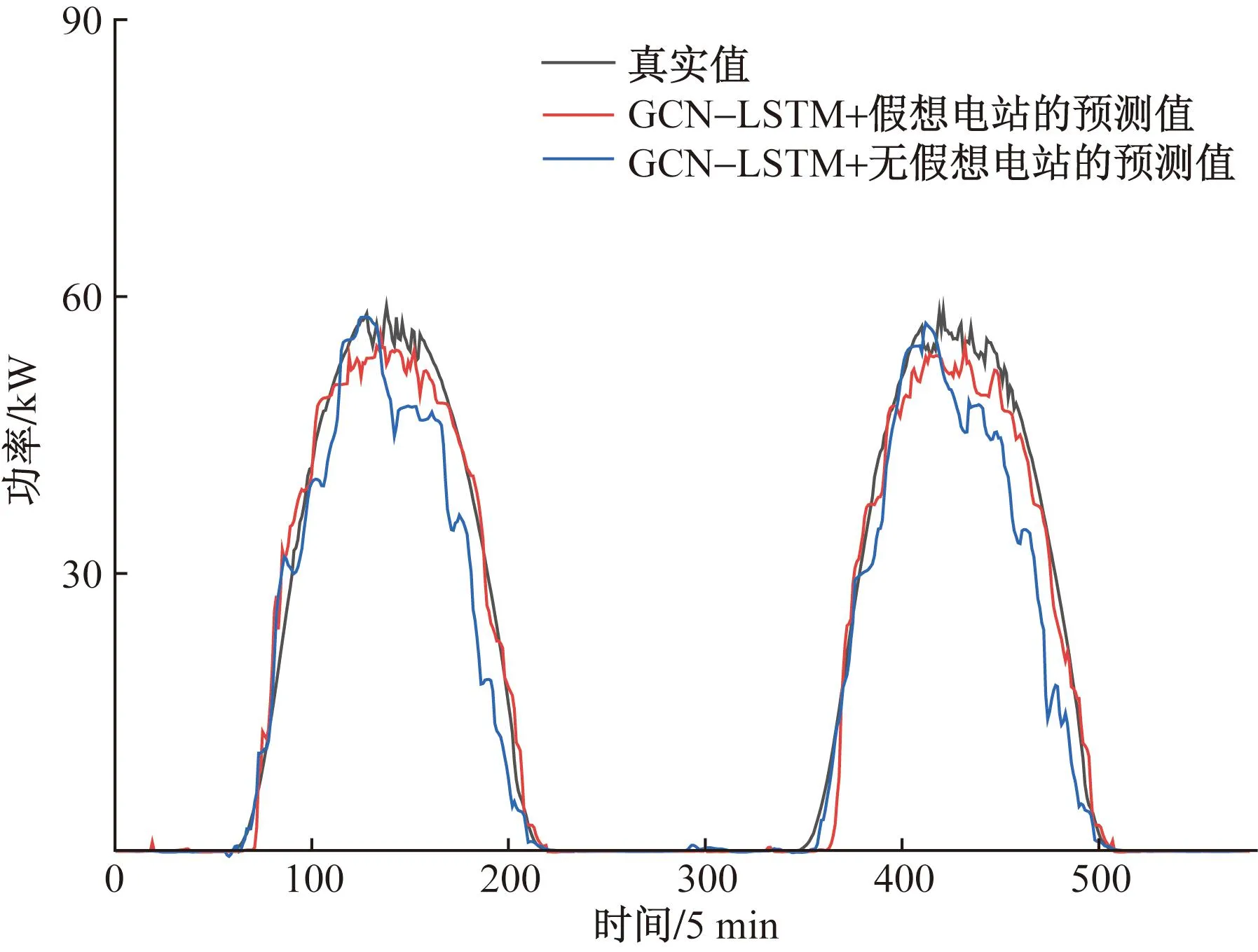
图10 有无假想电站的预测结果比较Fig.10 Comparison of prediction results with and without hypothetical power stations
4 结论
提出了一种基于GCN-LSTM算法的区域内光伏电站功率预测方法,得出以下结论。
(1)基于GCN-LSTM算法光伏电站预测功率的方法能够更加充分挖掘电站间的时空相关信息,预测效果优于文中的对比算法,具有更高的预测精度。
(2)通过假想电站增加一个图卷积网络的特征节点,能够减少预测模型的数量以及误差的来源,能够更为准确地预测区域内的电站总功率。
(3)与静态的时空相关信息相比,动态的时空相关信息更能挖掘区域内电站总功率与各个电站之间的时空相关性,提高预测精度。
