管道冲蚀液-固数值模拟的研究进展

2024-01-12李美求刘方张昆陈星彭翰林

科学技术与工程 2023年34期

李美求, 刘方, 张昆, 陈星, 彭翰林

(长江大学机械工程学院, 荆州 434023)

流经管道的流体中常会裹挟着大小不一、形状各异的固体颗粒,这些颗粒对管道内表面可造成材料去除作用,这种现象称为固体颗粒冲蚀[1],从而导致管道及其附属服务设备发生故障,这种故障在石油和天然气行业尤其突出[2-3]。管道及其设备的维护既昂贵又耗时,因此预测和研究控制固体颗粒的冲蚀具有重要价值。此外,预测弯管、汇管的抗冲蚀能力可以帮助设计师在管道布局排列时,将冲蚀的风险降至最低,从而降低设备维护成本。目前中外学者对冲蚀磨损的研究主要有实验和数值模拟两种方法[4-6]。一般来说,搭建一套研究冲蚀的具体实验室投资成本较高。20世纪90年代,Fluent软件中的计算流体力学(computational fluid dynamics,CFD)在预测固体颗粒引起的冲蚀中得到了广泛的应用,被科研人员认为是在冲蚀范畴内一种非常有价值的辅助工具,可通过大量的计算模拟和最少数的物理实验来研究冲蚀现象。该工具极大地促进了冲蚀模型的发展,并提出了几种广泛使用的基于CFD的冲蚀模型。然而,尽管数值求解模型和方法不断发展,处理大计算量和高复杂程度的能力越来越强,但物理实验仍然至关重要。主要原因是,描述某些问题的守恒物理量所需的控制方程大都是基于经验方程;此外,通过数值模拟所获得的结果需要进行理论模型和具体物理实验共同来评估数据的可信度。既验证评估了计算模型提供的解的数值精度,又确定了模拟结果与通过物理实验获得的数据之间的一致度。因此,在对冲蚀磨损的研究过程中,同时进行数值模拟和物理实验是一种必要常见的手段[7-8]。

由于冲蚀是一个复杂的过程,受许多因素的影响,仅凭经验模型是不够的,因为模型中缺乏理论论证,而较为复杂的模型又需要全面且多学科交叉的专业知识才能得出理论结果。因此,基于CFD的冲蚀模拟程序可靠性和精确性的开发与使用,甚至可能优于其自身模型的简化,对油气行业和冲蚀模拟界有更重要的意义。现着重对在管道冲蚀过程中携固液体的流动属性、固体颗粒的运动属性和冲蚀数值模拟3个方面进行综述,对比各种冲蚀模型在仿真软件下的适用性和预测效果,讨论仿真在冲蚀领域内所做的深度及以后研究的重点。

1 冲蚀理论的发展

在表面材料去除方面,目前存在以下4种机制,如图1所示。这4种机制包括切削(以切削刃穿透塑性材料)、疲劳(循环破坏)、熔化(失去流体状态)和变形断裂(塑性变形和脆性断裂)。冲蚀模型的建立通常是这些机制的组合。

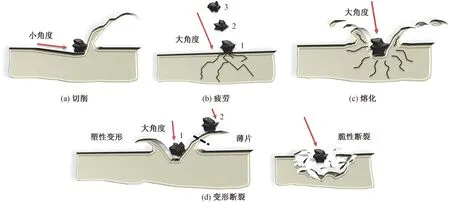
图1 表面材料去除的4种机制[9]Fig.1 Four mechanisms of surface material removal[9]

Finnie[10]在1958年首次对塑性材料提出微切削理论。以切削为主要的冲蚀机制,颗粒通常以小角度冲击,一个颗粒撞击靶材表面形成凹坑,下一个颗粒会撞击表面并从第一次撞击中移除剩余的材料,如图1(a)所示。只有颗粒在低入射角进行攻击靶材时,微切削理论才能比较完善地解释冲蚀情况。当颗粒冲击角度过大时,其模型与物理实验数据偏差较大。然而,对于脆性材料,Finnie[10]讨论了当颗粒以大角度撞击表面时,初始裂纹生成的条件,但无法提出与塑性材料类似的脆性材料模型。由于冲蚀颗粒入射角度的差异,部分研究者试图求解颗粒的运动方程,并通过颗粒撞击靶材表面的路径来预测冲蚀量。固体颗粒的冲击角度对塑性材料和脆性材料冲蚀量的函数关系如图2所示。

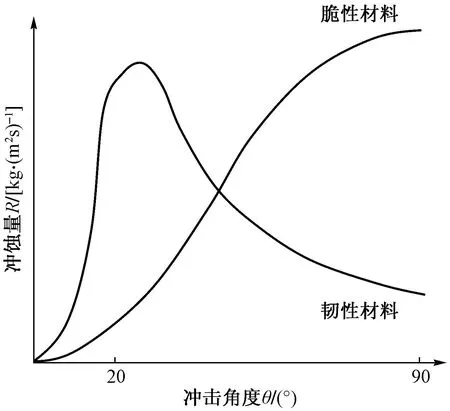
图2 冲击角度对不同类型靶材冲蚀量的影响[11]Fig.2 Effect of impact angle on erosion amount of different types of targets[11]

在Finnie[10]的基础上,Bitter[12-13]于1963年提出了冲蚀变形磨损理论。当固体颗粒冲蚀靶材表面时,若粒子的冲击应力未超过表面材料的屈服强度,材料表面出现弹性变形现象,若超过表面材料的屈服强度,则会引起材料表面的塑性变形,此为第一阶段。第二阶段与Finnie[9]的微切削模型相互一致。Bitter[12-13]认为冲蚀磨损的总磨损量应为变形磨损和切削磨损两者之和。Bellman等[14]和Levy等[15]在1981年提出了锻造挤压成片理论,固体颗粒冲击靶材时其表面受到挤压,形成薄片状突起和毛刺形凹陷但均未从表面脱离;凸起的片状金属层不断被固体颗粒冲击,而后脱离靶材,如图1(d)所示。这一理论被多数研究者所支持。对于脆性材料,在最初碰撞后出现裂纹网格,然后在颗粒反复冲击后,这些裂纹相交并从表面向内部断裂,如图1(b)所示。Sheldon等[16-17]和Evans等[18-19]研究了横向裂纹和纵向裂纹的成长机理,认为脆性材料冲蚀模型的建立始于裂纹的出生和成长过程。除了上述具有开创性的经典理论外,后续的研究者们还提出了一系列关于脆性材料冲蚀率V的理论模型如表1所示,并进行了扩展和补充,得出具体的冲蚀率V与冲击粒子自身参数的相关关系,表达式[9]为

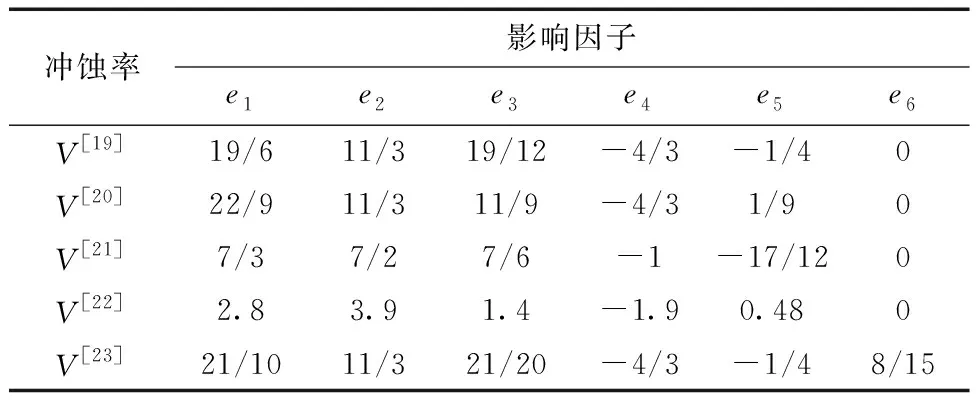
表1 各种脆性材料冲蚀理论模型参数Table 1 Erosion theoretical model parameters of various brittle materials

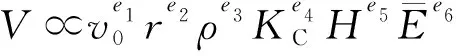
(1)

(2)

式中:e1、e2、e3、e5、e6为影响因子;v0为冲蚀速度;r为冲击颗粒的尺寸;ρ为颗粒密度;KC为靶材的断裂韧性;H为靶材硬度;vt为靶材的泊松模量;vp为冲击颗粒的泊松模量;Et为靶材的杨氏模量;EP为冲击颗粒的杨氏模量。

考虑到影响冲蚀的参数较多,到目前为止,已经确定多个影响固体颗粒冲蚀的因素,如图3所示,其中包括颗粒撞击速度、颗粒撞击角度、颗粒特性(如材料、形状、尺寸、锐度)以及目标表面特性(如材料、硬度、延展性和流动条件)等。Finnie[10]、Tilly[24]和Mansouri等[25]认为这些参数会显著影响固体颗粒冲蚀机制。研究者们开发了各种冲蚀方程[26-27],试图考虑不同的条件和尽可能多的影响因素。这些冲蚀方程可分为三大类:一是基于粒子运动的物理特性和施加在粒子上的作用力来预测冲蚀的数学模型而得到的纯理论方程;二是基于大量的具体物理实验而得到的纯实验数据(经验)方程;三是前两者的结合,即半经验-半理论方程。Grant等[28]、Oka等[29]、Zhang等[30]和Huang等[31]提出了冲蚀研究和文献中常用的方程。近年来,许多研究也采用计算流体力学(CFD)的方法对冲蚀现象进行了研究。Shirazi等[32]开发了一个半经验模型,该模型用于预测管道几何结构中的冲蚀以及弯头和三通中的冲蚀。Chen等[33]和Vieira等[34]也试验了三通和弯头相关方面的冲蚀。尽管如此,没有一个模型适用于所有情况。在复杂的流体介质环境下,固体颗粒对材料表面冲蚀的研究中,单一的某种冲蚀理论不能对冲蚀现象做出较为完整的解释,应该为多种表面材料去除机理之间的交互耦合,从而进行相互补充。

2 冲蚀过程中液体的流动属性

在液固耦合流场分析的过程中,将其分为液体流动属性和固体颗粒运动属性,分别从这两大属性进行阐述,如图4所示。在液体流动属性中,涉及流动控制方程,如质量、能量及动量的守恒方程。除此之外,根据雷诺数的大小不同,将流体划分流动状态稳定的层流和不规则紊流流场的湍流。根据实际工况,使用恰当的层流模型和湍流模型。而在进行模拟弯管和管汇冲蚀时,使用最多的为湍流模型。本节主要讨论流动控制方程和湍流模型。

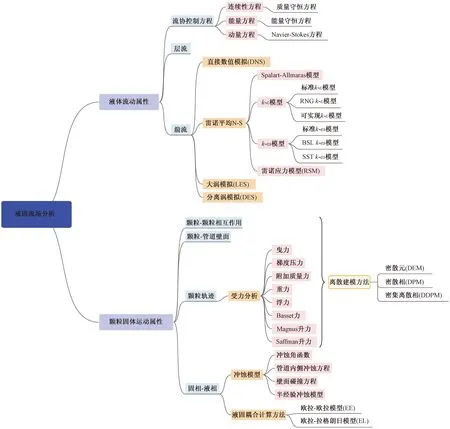
图4 液固耦合流场分析[35]Fig.4 Analysis of fluid solid coupling flow field[35]

2.1 流动控制方程

所有的流体问题,必须遵守这3个基本物理学原理:质量守恒定律、牛顿第二定律和能量守恒定律,由于研究的对象为固液流场,此为不可压缩的流体,在流动控制方程中将不再考虑其状态方程,则质量守恒方程、能量守恒方程、动量守恒方程如下[35]。

质量守恒方程为

(3)

能量守恒方程为

(4)

动量守恒方程为

(5)

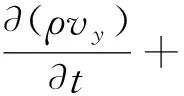
(6)

(7)

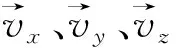
2.2 湍流模型

目前模拟流动的主要技术有3种[36],主要不同在于它们如何在不同尺度上处理湍流。一种是直接数值模拟(direct numerical simulation,DNS),求解Navier-Stokes(N-S)方程,甚至到最小尺度的流动,所有湍流涡流都被完全解析且全部被模拟显示,因此在计算上是非常昂贵的,这种模拟对绝大多数流体流动问题不是实用的解决方案。一种是大涡模拟(large eddy simulation,LES),该技术显性地解决了大规模涡流,但小规模涡流被过滤掉并用子网格模型进行建模,LES的计算成本远低于DNS。分离涡模拟(detached eddy simulation,DES)是LES的一种替代方法[37]。另一种雷诺平均法(reynolds average navier-stokes,RANS),这是3种技术中计算成本最低的时间平均方法,基于Boussinesq假设,在时间域上对流场物理量进行平均化处理,求解所得到的时均化控制方程,从而使用湍流黏度的概念来模拟涡流流动。目前存在几种不同的湍流模型,如k-ε模型、k-ω模型、雷诺应力模型(reynolds stress models,RSM)和Spalart-Allmaras模型等。不同的模型适合不同的问题类型。常用的几种湍流模型及优点和适用范围如表2所示。

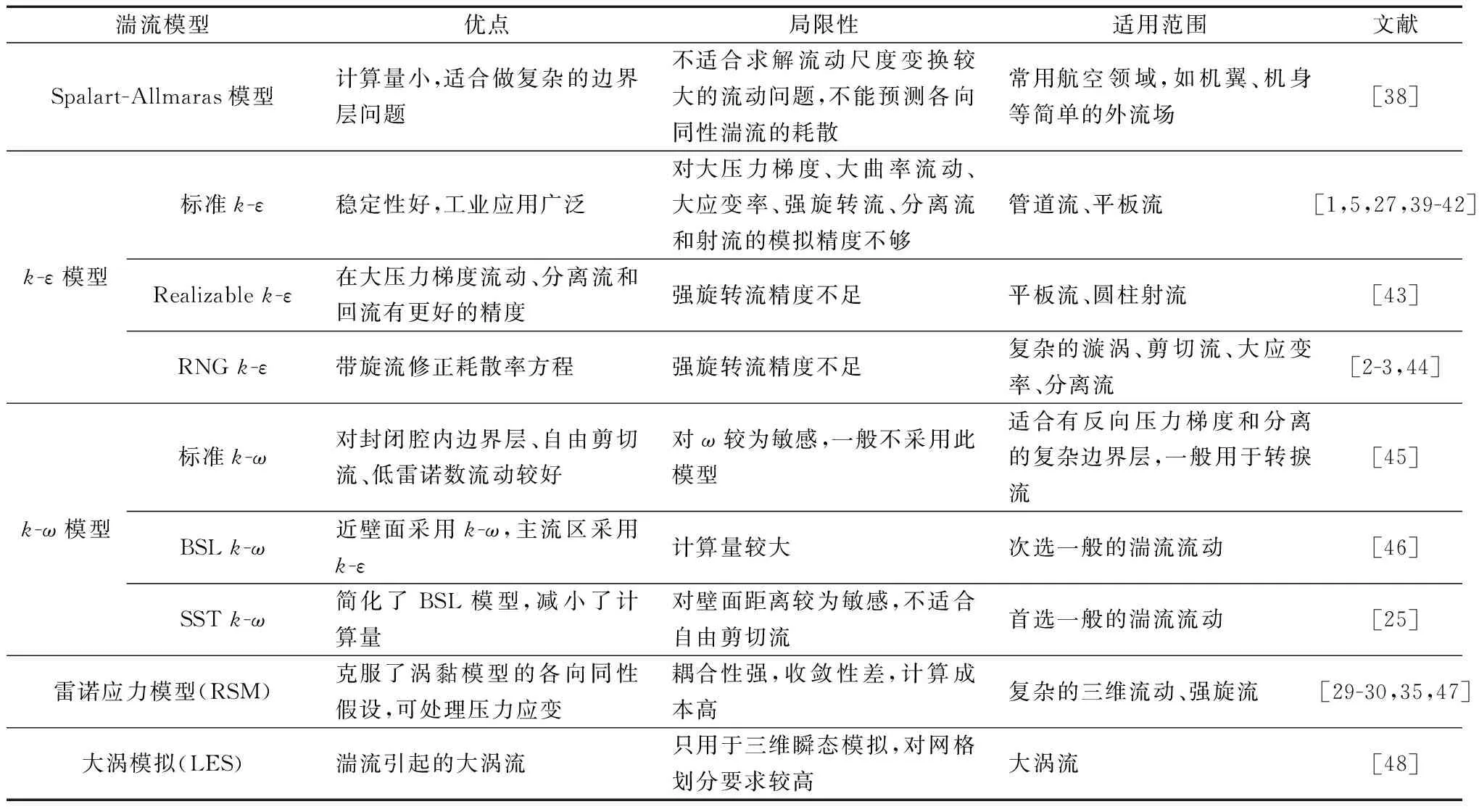
表2 常用湍流模型Table 2 Common turbulence models

从表2中可以看出,使用k-ε模型较多,由于其稳定性好,工业应用较为广泛,多受研究者的青睐,但该模型在近壁面时采用壁面函数处理,从而导致壁面处理精度不够。近年来有多种低雷诺数k-ε模型通过计算黏性子层进行修正[49],以提高近壁面精度。此模型日益完善逐步成为当今主流。k-ω模型是直接求解边界层网格数据,近壁面处理较好,对逆压梯度和分离流动处理比k-ε模型计算更为精确。在涡黏模型中,BSL近壁面采用k-ω,主流区采用k-ε,集两模型之优点,而SST是对BSL的简化版,减小了其计算量。RSM模型支持各向异性流动,用于强旋转、大曲率流,二次流、浮力流等复杂的三维流动,但由于计算成本高,在工程应用中受到限制。LES模型主要用在瞬态大涡流流动模拟,对网格划分要求较高。

3 冲蚀过程中固体颗粒的流动属性

以流动介质中的分散相-固体颗粒为研究对象进行粒子跟踪,用离散建模法来表示颗粒-颗粒相互作用和颗粒-壁面的函数关系,分析固体颗粒在流动液体中受力情况,考虑其自身是否有上下自旋及运动轨迹。在固液耦合两相流中,选取较为合适的冲蚀模型,在计算方法上,有欧拉-欧拉模型(euler-euler model,E-E)和欧拉-拉格朗日模型(euler-lagrange model,E-L)。在该部分内容中主要探讨离散建模和冲蚀模型。

3.1 离散建模方法

在计算颗粒轨迹和对粒子跟踪采用最多的方法是离散相建模法。E-E或E-L都可用来模拟质点运动。当固体颗粒体积分数小于10%,其颗粒视为离散相分散在连续相的流体中,考虑每个粒子的运动状况,并沿粒子的轨迹计算相关变量,而当粒子之间的相互作用可以忽略时,E-L的计算是高效的。对于颗粒浓度相对较高的流动,液相和颗粒相都被视为连续相,在靠近壁面处,质点的运动包括撞击和反弹,E-E仅给出质点在每个控制体积内的运动平均值。这可能会导致预测颗粒的冲击速度不准确,进而影响冲蚀的预测[50]。

在离散相模型(discrete phase model,DPM)中,离散相粒子的运动轨迹由拉格朗日系统中粒子作用力的微分方程确定。作用于粒子的流体力决定了它们的轨迹,通过求解质点运动方程来计算每个质点的运动。对颗粒受到的流体力进行分析,根据具体工况对受力进行简化。常用的质点运动方程为

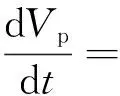
(8)

式(8)中:等式左侧为质点惯性;Vp为颗粒速度;右侧为作用在质点上的力;FD为曳力颗粒受到最重要的力(颗粒所受液体的阻力);FV为附加质量力,表示颗粒被加速或减速时所取代的流体体积,当流体密度与颗粒密度之比较大时,该力不可忽略;FP为压力梯度力,当粒子通过具有高压力梯度的区域时(如变径流道),压力梯度所产生的力对粒子轨迹有重要影响;FG为颗粒受到的重力;FB为颗粒受到的浮力;FBa为巴塞特力,由于液体黏性引起颗粒的速度变化,其本质是瞬时阻力;FM为Magnus升力,颗粒自身旋转而产生的升力;FS为Saffman升力,当颗粒两侧的液体流速不一样时,由伯努利原理,高速度区会“吸引”低速度区颗粒。研究者可由上述8种受力状况根据实际流动状态对力做出取舍,展开式的适用范围见文献[7,51]。

在上述离散相模型中,考虑到颗粒碰撞壁面后会反弹,这个反弹的角度与颗粒入射角度大小是否相等,这两个值存在什么样的函数关系,就需要恢复系数来进行表征。Grant等[28]提出的随机颗粒-壁面碰撞反弹模型和Forder等[52]提出的非随机性颗粒-壁面碰撞反弹模型。分别用法向恢复系数和切向恢复系数多项式来表示。反弹模型实质上表征的是单个颗粒的能量有多少被靶(壁面)材料所吸收。目前常用的函数式是针对壁面材料为碳钢和不锈钢,如果材料特殊,则需要重新进行大量实验来确定和修正壁面反弹函数。

除了以上常用的DPM模型外,还有密集离散相模型(dense discrete phase model,DDPM)[53-54]和离散元方法(discrete element method,DEM)[55-56]。这3种方法最本质的不同是处理颗粒与颗粒之间相互作用的方式。DPM直接忽略颗粒与颗粒相互作用,而DDPM和DEM分别利用颗粒流动力学理论和软球模型来模拟颗粒与颗粒之间的相互作用。文献[7,57]详细讨论了这些模型本身及它们的使用方法和所涉及的各项参数。到目前为止,大多数关于冲蚀预测的研究是用DPM模型进行的。近年来,DEM模型在冲蚀研究中逐渐活跃起来。它可以捕捉颗粒和颗粒的相互作用、颗粒自身旋转和形状、颗粒冲击条件变化对壁面产生的冲蚀影响。然而,由于计算成本很高,从而限制了DEM方法的使用。Kuang等[58]采用了一种新方法,在DEM的基础上,在直管和弯头处的颗粒冲击速度、冲击角、周长角和碰撞频率采用统计函数建立一维冲蚀模型(one-dimensional erosion model,ODEM)来计算冲蚀率。与通过三维DEM模拟,提取碰撞动力学以生成统计函数相比,在精度一致的条件下,该方法能以更快的速度预测管道的冲蚀速率。

3.2 冲蚀模型

在3.1节中对颗粒进行建模时,无论选择哪种建模方法,DPM、DEM、DDPM、ODEM等方法,当颗粒撞击到壁面,相应的撞击信息就被存储起来,如颗粒冲击速度、冲击角度、颗粒的质量和流量等,这些信息将用于下一步的冲蚀计算。冲蚀模型将冲击信息与壁材的冲蚀率或质量损失建立联系。目前学者们已提出200余种经验或半经验模型来表达冲蚀速率[59]。常用的冲蚀模型贡献和局限性如表3所示。

表3 常用冲蚀模型Table 3 Common erosion models

冲蚀模型不管形式怎么变化,其函数式中都保有颗粒信息的常规参数,如颗粒速度、入射角、壁面反弹系数等,如图3所示。计算方法可能不一样,但计算出的结果均需要与实验室数据进行多次比较,从而得出具体选定哪个冲蚀模型较为合适。

4 管道冲蚀模拟

模拟冲蚀的目的就是在于预测管道服役寿命,监控流动状态,零部件的故障诊断和健康监测,预防安全事故发生和提高企业生产效率。截止到目前,对管道系统的冲蚀磨损仿真中,做了许多不同类型管道的冲蚀模拟,如图5所示,如不同角度弯管(如30°、60°等)、三通、四通、连续管道等。在CFD的模拟下,通过使用参数数值计算和合适的冲蚀模型,从而确定零部件的冲蚀速率(使用寿命)和最大冲蚀位置。除此之外,也对高压泵和涡轮机等复杂几何形状展开了冲蚀的研究。在整个大的管道系统范围内,可以将这些弯头和接头视为一个小单元,但这些小单元重新排列组合形成新的组合单元和管道系统,其耐冲蚀性能怎样去模拟和评估,目前研究的较少。这将会对今后管道系统在实际工况下的接头选型和整体位置布局有着重大影响。

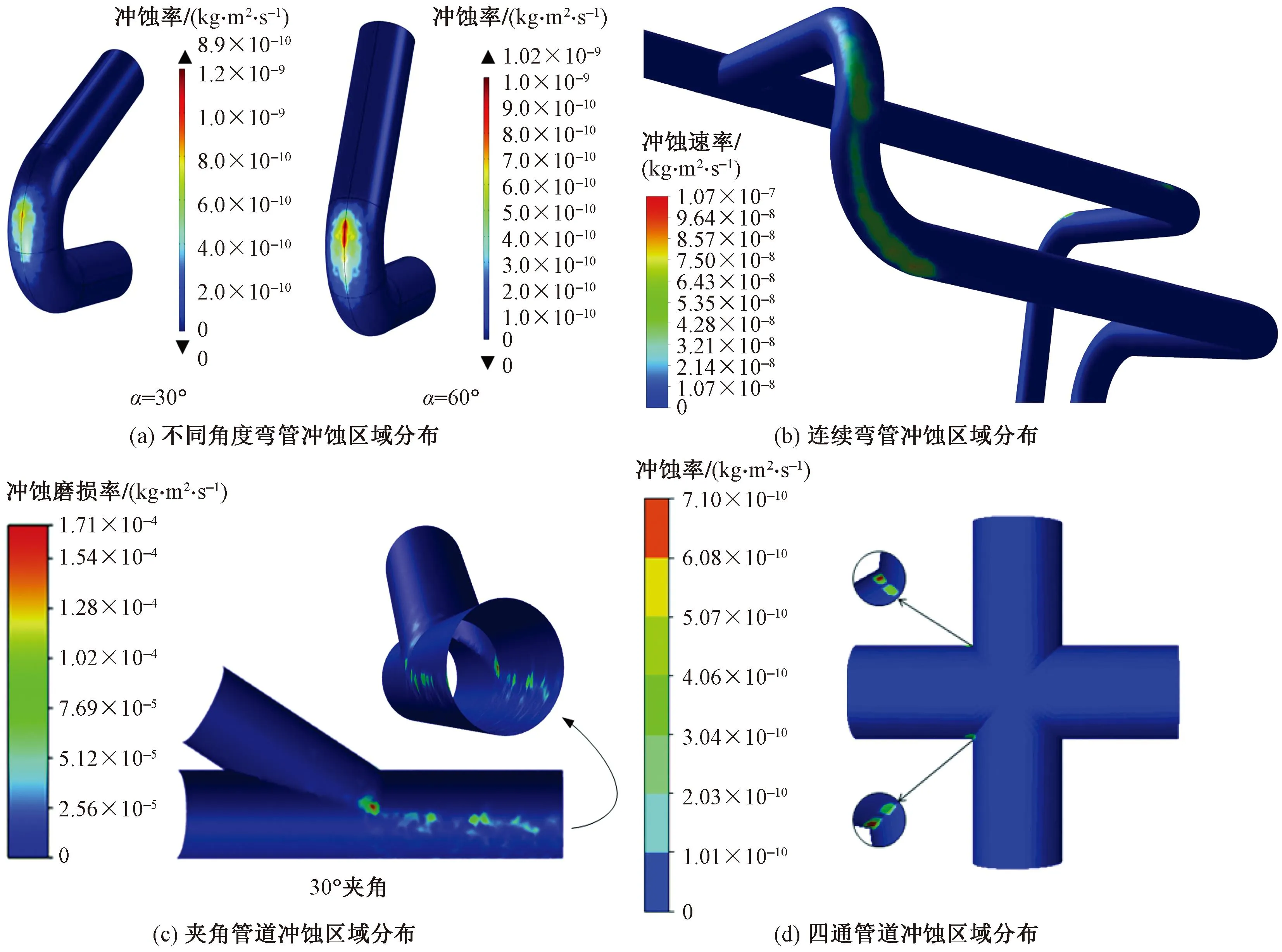
α为管道夹角图5 各管道接头冲蚀模型[57,42,61]Fig.5 Erosion model of each pipe joint[57,42,61]

多年以来,在进行管道冲蚀模拟时,网格无关性的验证是必须进行分析的,通常在模拟过程中采用的为不变形网格。这可能引起预测的冲蚀与现场的冲蚀较大偏差。目前López等[62]开发了一种包括网格变形的冲蚀计算方法。它既适用于欧拉方程,也适用于拉格朗日方程。利用该方法对渣浆离心泵套管进行了冲蚀模拟,得到了与真实套管基本相似的冲蚀模式。在计算冲蚀时,由于网格的存在失真,影响计算精度[61]。为了避免计算网格失真的问题,近年来出现了无网格方法。在不同的无网格方法中,“光滑粒子流体力学”(smoothed particle hydrodynamics,SPH)被广泛用于冲蚀建模中[63]。SPH使用拉格朗日粒子来表示目标材料,如其应力、应变和温度等变量信息,可以捕捉快速移动的界面和自由表面。其核心思想是使用一组任意分布的节点或粒子,为具有各种可能边界条件的积分方程或偏微分方程提供精确稳定的数值解。由于无网格特性,在模拟大变形和材料去除方面具有很大的优势。