基于深度强化学习的无人机姿态控制器设计

王伟, 吴昊, 刘鸿勋, 杨溢

(南京信息工程大学自动化学院, 南京 210000)

四旋翼无人机诞生于20世纪,在军事、运输、农业、航拍等活动中被广泛运用,无人机作为一种有4个控制输入以及6种状态输出的多输入多输出的强耦合的非线性的欠驱动系统,加上外界环境对无人机的各种干扰,无人机控制也面临着诸多难点。无人机控制主要包括位置控制、速度控制以及姿态控制,而姿态控制作为无人机的底层控制,尤为重要。学者们提出了众多姿态控制算法来优化无人机控制。

目前,比例积分微分(proportional-integral-derivative PID)算法是工业中被用到的主流的无人机控制算法,但PID的参数是通过多次实验和经验判断来选取的,所以难以满足动态性能的要求[1]。模型预测控制(model predictive control,MPC),是一种基于模型的闭环优化控制策略,在工业界的影响力仅次于PID控制,被广泛应用于机器人控制,相对于线性二次调节(linear quadratic regulator, LQR)和PID等只能考虑输入输出的约束,MPC可以综合考虑各种状态的约束,王晓海等[2]提出了一种基于模型预测控制和扩张状态观测器的复合控制器来解决无人机在干扰下的姿态跟踪问题,但也存在着比如对模型建立的准确度较高,优化问题计算量庞大,针对不同的环境需要设置不同的损失函数以及建立不同的模型,泛化性弱等问题。模糊控制不需要求解被控对象的数学模型,适用于大多模型参数不确定或者有着较大波动的系统,刘用等[3]提出了基于模糊控制的姿态控制算法来提升机器人的姿态稳定性,但其自适应能力有限,精度也不高,控制规则的优化也有着一定的困难。还有许多先进控制算法如滑模控制[4]、鲁棒控制[5]等也被广泛运用,但这些算法都有着一定的局限性,对环境变化的适应性较差,也不能适用于所有类型的无人机。

随着人工智能的发展,无人驾驶、人脸识别、图像识别、同步定位与建图[6]等领域都取得了重大的成功,基于深度学习的控制也展现出了巨大的潜力,强化学习作为机器学习的代表之一,已经被成功应用于各种控制算法,智能体通过利用行动与环境进行交互,根据所获得的奖惩来不断地学习与成长[7]。

在强化学习算法中,Q-learning和Sarsa是用于优化解决马尔科夫决策过程(Markov decision process, MDP)中的主流算法,但由于传统的强化学习有着一定局限性,因为其动作空间和状态空间往往都是有限大小的,且大多都是离散的情况,然而在实际无人机控制中,状态空间和动作空间都是庞大且连续的[8],所以确定性策略梯度(deterministic policy gradient, DPG)以及其优化版本Deep DPG(DDPG)等算法都能解决传统强化学习中的短板问题[9]。

李岸荞等[10]使用基于模仿专家经验的深度强化学习方法,实现了四足机器人的后空翻动作的学习,Zhang等[11]提出了基于模型的强化学习实现卫星的控制方法,Liu等[12]利用强化学习应用于水下航行器设计。此外,为了使强化学习算法更具有实用性,很多学者提出了一些优化算法,Long等[13]提出了一种基于单一批评家的神经网络的强化学习算法用于系统的最优跟踪,以及Han等[14]通过双重回放记忆来设计神经网络。Wang等[15]通过使用积分补偿器来消除DDPG方法中的稳定误差,但积分补偿器是一种外部的方法,他并不会直接解决控制器内部的问题。付宇鹏等[16]提出了一种基于强化学习的无人机姿态控制器设计,但其在追踪目标值的过程中虽然响应非常快速,但不可避免地带来了较大的超调。

基于此,现提出一种基于DDPG来设计的一种无稳态误差、鲁棒性强、动态稳定且快速响应的四旋翼控制算法,针对强化学习算法设计的控制器带来的超调的问题。在该方法中,结合Actor-Critic结构与参考模型,期望解决系统过于追求目标跟踪的快速性,从而导致控制量过大的问题。以期改进后的算法能有效地处理外部干扰和环境变化,对目标值响应快速,而且可以有效地解决超调和稳态误差的问题。

1 强化学习基础

强化学习的目的是为找到一个策略,智能体根据该策略在环境中采取行为动作(action)[17],每次动作都会带来不同的奖励(reward),最后获得了最大的奖励值的总和(total reward)。这个奖励与控制的目标相关[18]。强化学习解决的是马尔可夫决策过程(MDP),其正式框架如下:一个马尔可夫决策过程由一个四元组(S,A,P,R)组成,其中S是状态集,A是动作集,P表示状态转换概率函数,R表示奖励函数,其迭代过程如图1所示。

图1 智能体环境交互迭代Fig.1 Agent-environment interaction iteration

智能体首先观察当前环境的状态St∈S,然后根据策略πa,a是表示该策略的参数,采取一个行动at∈A,与环境进行交互。在动作at作用下状态由St∈S转化为St+1∈S,同时环境会立即给Agent一个奖励rt∈R(st,at),作为MDP问题,对于每一个状态-动作s1a1...snan之间的转化都要遵守具有条件概率的平稳转换动态分布:P(St+1|S1,a1,…,St,at),即状态S1转化为状态Sn的概率为P。

(1)

式(1)中:Vπ(st,at)为状态s的价值函数,表示在状态s下的预期累计奖励;R(s)为在状态s下采取动作后取得的及时奖励;γ为折扣因子,表示未来奖励的折扣比例;Vπ(s′)表示下一个状态s′的价值函数,无人机控制的主要目标是找到合适的控制策略,可以帮助无人机快速稳定地到达所期望的状态,现在可以用一个全新的方法--强化学习来实现这个目标,在时域中,选择了适当的动作和状态,将无人机的动态模型形式假设为MDP。在处理连续的状态和动作的问题的时候,策略梯度算法是一个很好的选择,参数化的随机策略πθ(s,a)可以直接生成控制动作,使用参数ϑ,在给定状态S的情况下,采取动作a。然后根据梯度来调整参数以此来改善策略。

∇θJ(πθ)=Es～ρπ,a～πθ[∇θlnπθ(s,a)Qπθ(s,a)]

(2)

式(2)中:∇θJ(πθ)为关于策略参数θ的梯度;E为智能体在不同状态下根据策略做出动作的概率的期望值;πθ(s,a)为根据策略参数θ做出动作a的概率分布;Qπθ(s,a)为选取动作a的动作价值函数,表示采取动作后的累积奖励,这是一种随机策略选择算法,但在实际无人机控制中,随机策略是危险且无法预测的,这种基本方法无法处理无人机复杂的非线性控制问题。

这些年来,通常使用一些确定性策略来改进算法,本文就是在它们的基础上建立起来的。

2 控制器设计

2.1 姿态模型的建立

四旋翼无人机的动力学模型构建较为复杂,如图2所示。

F1～F4为电机控制产生的升力;θ为无人机的俯仰角;γ为无人机的横滚角;φ为无人机的偏航角图2 四旋翼无人机模型Fig.2 Quadcopter drone model

四旋翼无人机控制系统XY轴上主要由姿态控制、速度控制、位置控制组成,Z轴上主要由高度方向的速度控制以及高度方向的位置控制组成,本文主要研究的为四旋翼无人机的姿态控制器,所以只需建立四旋翼无人机的子系统的数学模型。由于无人机的俯仰和横滚姿态角速度目标值和姿态角速度之间存在着一阶惯性环节,即

(3)

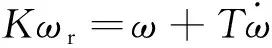
(4)

(5)

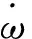
由式(3)可以得到其状态方程系数A和B以及输出方程的C表示式为

(6)

(7)

(8)

D=[0]

(9)

在经过无人机实地飞行后,采集飞行数据,之后由MATLAB的IDENT工具箱,根据式(3)进行数据拟合,可以得到K=1,T=0.072 172。

如图3所示是飞机实际飞行数据以及模型数据的对比,其中蓝线为模型拟合的数据,黑线为实际飞行的数据,可以看到两个曲线基本保持一致,可以认为本文动力学模型的建立是正确有效的。

图3 模型建立数据对比Fig.3 Data comparison of models

2.2 DDPG算法的设计

本文所用的RM-DDPG(reference model-deep deterministic policy gradient)算法的基础是DDPG算法,对于随机策略梯度而言,在一个状态下选取动作的依据是一个概率分布,即具有不确定性。而确定性策略梯度采用确定性策略来逼近actor函数,取代了原策略梯度法中的随机策略。事实上,确定性策略是随机策略的一种极限情况。该算法的核心思想就是使用动作函数πμ中的参数μ来表示策略,然后沿着式(10)的梯度的方向不断优化参数μ[19]。

Es～ρπ,a～πα[∇απα(s)∇aQπα(s,a)]

(10)

式(10)中:∇μJ(πμ)为Actor网络的梯度;ρπ(s)为状态分布;∇α为取动作的梯度。

式(10)中Qπα(s,a)实际上是状态价值函数,其中很重要的一点是,如上文所说,对于确定性策略,给定状态s和策略参数θ时,其选取的动作是固定的。也就是说,当初始状态已知时,用确定性策略所得到的行为轨迹永远都是不变的,所以用什么来选取行动价值函数Qπ(s,a)是极为重要的,所以本文研究中整个确定性策略的学习框架都采用AC(actor-ritic)算法的方法。在AC体系中,包括两个地位相同的元素,一个元素是Actor即行动策略,另一个元素是Critic即评估策略。价值函数Qπ(s,a)被另外一个价值函Qω(s,a)代替,用Qω(s,a)来逼近Qπ(s,a),使得Qω(s,a)[20],其中ω为待逼近的参数,actor函数的参数以确定性策略梯度的方法更新策略参数。

θt+1=θt+αθ∇θπθ(st)∇aQω(St,at)|a=πμ(s)

(11)

式(11)中:αθ为学习率。

DDPG算法中的AC结构如图4所示。

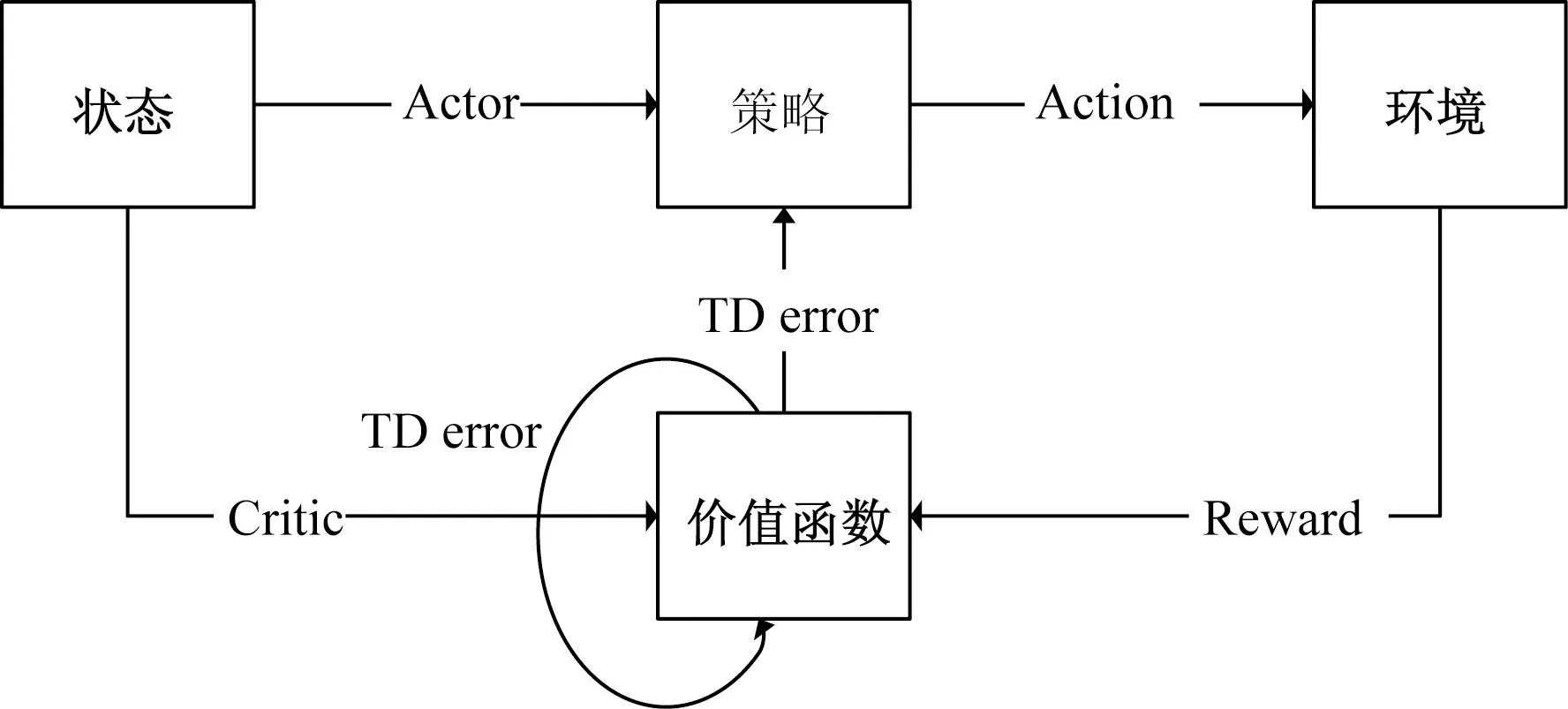
Actor为策略网络;critic为评价网络;Action为智能体根据策略而采取的行动图4 Actor-Critic结构Fig.4 Actor-Critic structure

根据贝尔曼方程,利用值函数逼近的方法更新值函数参数[21],所以本文研究中定义了TD差误差(temporal difference error,TD error)。

δt=rt+γQω[St+1,πμ(St+1)]-Qω(St,at)

(12)

并且选取了一种简单的确定性梯度下降策略来减小TD误差,即

ωt+1=ωt+αωδt∇ωQω(St,at)

(13)

式(13)中:ωt为策略参数;αω为学习率;δt为关于参数的梯度;∇ωQω(St,at)为动作价值函数关于动作a的梯度,表示状态S下采取动作a的梯度。

由于四旋翼无人机控制是一个复杂的非线性问题[22],而且它的状态和动作都是连续且庞大的,因此,通常很难估计actor函数和critic函数,所以本文研究使用神经网络来代替actor函数和critic函数。为了提高训练的效率和稳定性,还应用了经验数据重放并且设计了目标网络。

大多数优化算法通常都是假设实验数据样本是相同分布且独立的,当样本是在同一个环境中选取的时候,就会出现经验数据的相关性和非平稳分布的问题,所以本文研究设计一个大小为M的回放缓冲区D={e1,e2,…,em}来存储样本,e表示单位训练时间步长中的经验数据,其数据类型为{st,at,rt,st+1}。缓冲区的长度是有限的,当缓冲区存储满的时候,最早的样本数据会被丢弃。每个单位训练时间步长都会随机均匀随机从缓冲区内采样,来更新Actor网络和Critic网络。通过这种方法数据的相关性将大大减小。此外,还设定了一个目标网络,以进一步提高学习的稳定性,针对Actor-Critic网络的更新不仅仅是简单的权重的复制,而是进行数据的软更新,在训练开始的时候,用Critic网络克隆一个目标网络,在每次学习迭代的时候,目标网络的权重将以较小的更新率缓慢地与Critic网络同步,假设速率μ≤1,则有ω′=μω+(1-μ)ω′。其中分别定义Qω′(s,a)表示Critic目标网络,ω′为Critic目标网络的权重。由于参数更新比较缓慢,学习的稳定性大大提高。因为需要加入经验回放的方法,还需要重写Critic目标网络的更新方程,对经验缓冲区内的经验数据(si,ai,ri,s′i)进行重新采样后,通过最小化损失函数,来更新Critic网络。

(14)

yi=ri+γQ′[si+1,μ′(si+1|θμ′)|θQ′]

(15)

式中:Qω(si,ai)|θQ为Critic网络在当前状态和动作下的估计动作值函数;yi为带有行动奖励的Critic目标网络的输出;ri为当下状态的实时奖励;γ为折扣因子,即未来奖励的折扣比例;μ′(si+1|θμ′)|θQ′为目标策略网络在下一状态下的预测动作。

更新Critic网络参数的公式为

(16)

ωt+1=ωt+αω∇ωLoss(ω)

(17)

同时,需要按照DDPG算法更新actor网络参数,即

(18)

μt+1=μt+αμ∇μJ(μ)

(19)

根据文献[14]和文献[16]中的研究究可以发现,DDPG算法在四旋翼无人机控制中存在两个问题分别是控制饱和以及稳态误差。

关于稳态误差,实验结果表明,在大多数情况下,无论给予控制器多长时间,或者什么样的训练策略,或者训练需要多少次迭代,稳态误差总是存在的。其中有两个原因:第一个原因是,动作值函数估计不准确,即使在非常简单的控制任务中,也无法准确地获得动作值。对于四旋翼无人机控制等复杂任务,估计动作值的准确性要低得多。另一个更重要的原因是,由DDPG算法训练的控制器不是伺服系统,因为它没有考虑误差积分,对于具有阻尼和外部干扰的系统,稳态误差无法通过这种方式消除。通过采用角速度误差的积分作为扩展状态代入控制器,可以有效地消除稳态误差。

控制量饱是一个在控制算法设计中常见的问题[23]。在算法中总是以被控对象能否快速追上目标值作为判断算法是否优秀的一个指标,但在四旋翼无人机的控制中,假如控制量过大,会导致无人机直接侧翻,与无人机实际物理运动原则不符。可以发现,奖励的设置是解决这一问题的关键,在通过最小化损失函数更新批评家网络的过程中,奖励是每次迭代的重要基础。当前TD误差算法获得的奖励是一个简单的标量,仅仅为四旋翼无人机的目标姿态角和反馈姿态角之间的误差。这种获得奖励的策略对于复杂的任务而言不能满足需求,在四旋翼无人机中受控对象有许多重要的状态量:角、角速度、角加速度,所以控制目标不仅是尽快跟踪目标的姿态角,系统的稳定性也要被考虑在内。为了解决这个问题,进一步改进了奖励的形式,即

(20)

式(20)中:Ref(sj)为所有状态的目标值;sj为所有状态变量,包括角度、角速度和角加速度;αk为可设定的权重。

2.3 参考模型设计

本文研究中添加了一个参考模型,来设计一个具有高稳定性和动态性能的四旋翼无人机控制系统。根据目标产生参考信号,并对四旋翼无人机模型进行重新分析,选择角度、角速度、角加速度和角度误差积分作为状态变量,建立指定的参考模型,即

(21)

ym=Cmxm

(22)

式中:um为参考输入。

设置e=x-xm,可以获得状态变量误差,为了消除稳态误差,提出了一种新的状态估计方法ζy,即

(23)

最后,得到了一个三阶参考模型,状态变量分别为角加速度、角速度和角度目标值。四旋翼无人机的模型的状态变量为角加速度、角速度和角,角误差的积分。这是一个标准的可以快速稳定响应的伺服系统。

2.4 RM-DDPG控制器设计

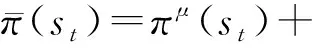
Critic网络的输入是四旋翼无人机的状态、参考模型的状态以及Actor网络生成的控制输入,其隐藏层和激活函数类似于Actor网络。此外,为了更快更好地训练Actor网络,Critic的输出层更换为一个线性的激活函数。

Reward为所有状态误差error的总和,作为反馈输入到系统,这样处理就可以使得Actor网络在输出的时候规避系统存在的稳态误差。

在做完以上处理后,可以使得控制信号可以快速而稳定地追上参考模型的输出,同时可以避免控制量太大导致追踪目标角度的速度过快从而产生的系统超调,并且可以有效地弥补稳态误差。

由于四旋翼无人机具有对称的结构,所以俯仰和滚转的控制器结构是相同的。

如表1所示是算法的流程,首先克隆一个Critic网络作为Critic目标网络,之后Actor网络给四旋翼无人机模型输出控制信号,参考模型也会输出一个目标值,同时,对于每一训练步长而言,训练的模型的状态都会被存储在记忆缓存区内,当存在了足够多的样本时就开始训练。

表1 RM-DDPG算法Table 1 RM-DDPG algorithm

3 实验和实验结果分析

3.1 参考模型仿真与神经网络的训练

对于无人机模型,选择了一种电力四旋翼无人机。然后用测量的无人机参数识别了动态模型为了使系统在快速响应的基础上,更具有稳定性,设计了姿态参考模型,阶跃响应如图6所示。

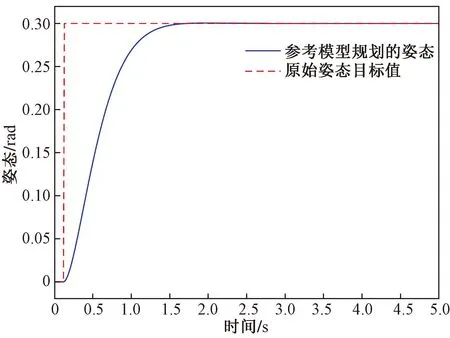
图6 参考模型设计效果图Fig.6 Design diagram of the reference model

神经网络和模型的建立用的是python和pytorch,如图7所示,是每个训练步骤的累积奖励,可以看到reward不断地在收敛。

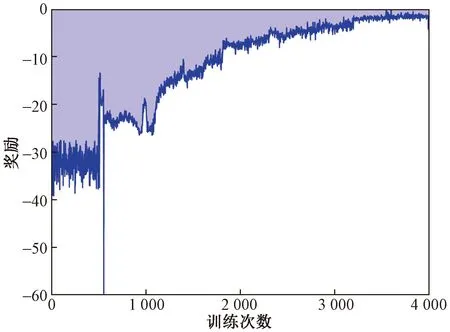
图7 Reward值Fig.7 Reward value

3.2 阶跃响应测试

设计了一个模拟测试,设置目标姿态角为0.3弧度,图8是无人机在追踪目标姿态角的性能图,可以看到姿态追踪过程中,没有出现超调与稳态误差。图9显示的是姿态角与目标姿态角随着时间变化的误差,在追踪的过程中始终保持较小的值。图10表示的是角速度的追踪性能,图11显示的是其角速度与目标角速度的误差变化,可以发现与角度追踪一样,角速度的追踪也没有出现超调与稳态误差,追踪误差也始终保持在较小的范围内。

图8 阶跃响应-角度状态变化Fig.8 Step response-angular state change

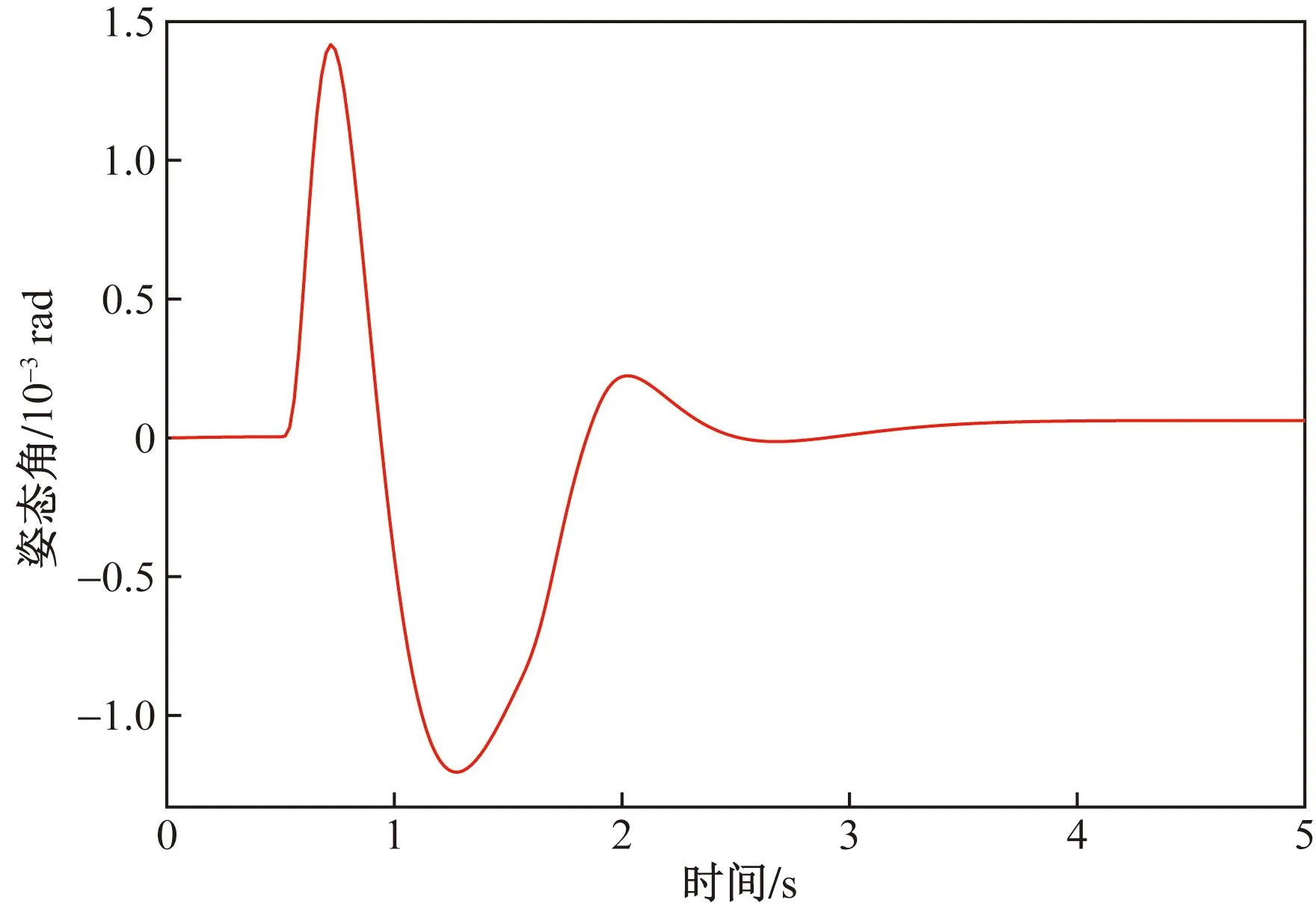
图9 阶跃响应-角度误差变化Fig.9 Step response-angle error change

图10 阶跃响应-角速度状态变化Fig.10 Step response-angular velocity state change

图11 阶跃响应-角速度误差变化Fig.11 Step response-angular velocity error change

由RM-DDPG算法的实验结果可知,无人机的控制输入因为参考模型的加入不会直接达到最大值而饱和,它可以比较缓和地追上目标值,因此该控制器较为稳定,并且从图11可以发现消除了稳态误差。

3.3 鲁棒性测试

为了进一步验证控制器的鲁棒性,在原有模型的基础之上对部分参数进行修改,来模拟无人机在实际飞行过程中可能出现的未建模误差以及干扰,模拟了不同模型下的无人机进行实验。图12是不同机型的在姿态角追踪上的表现,图13为不同机型的姿态角追踪误差,实验表明,RM-DDPG算法在不同的机型上,姿态角的追踪效果都是较为良好的,可以平缓地追上目标值,追踪误差始终保持在较小的范围内,并且都没有稳态误差以及超调,具有较好的鲁棒性。

图12 鲁棒性测试-角度追踪Fig.12 Robust test-angle tracking

4 结论

针对四旋翼无人机的非线性的强耦合以及欠驱动的特性,设计了一种基于深度确定性策略梯度算法和参考模型的四旋翼无人机的姿态控制器,对无人机模型进行了分析及简化,建立了四旋翼无人机的姿态模型,找到造成控制量饱和以及存在稳态误差的原因,通过设计参考模型解决了这两个问题,经过训练后,依据给定的目标姿态角的阶跃响应测试结果表明:①该算法有效地提升了系统的稳定性,消除了稳态误差具有良好的泛用性;②根据鲁棒性实验结果表明,该算法有优良的鲁棒性。