基于非支配排序遗传算法的沥青路面大中修养护决策
2024-01-12马士宾徐梓菲刘月钊宋玮卓
马士宾, 徐梓菲, 刘月钊, 宋玮卓
(河北工业大学土木与交通学院, 天津 300401)
沥青路面具有行驶舒适、噪音低、便于养护维修等优点,在高等级路面中被广泛采用。但随着中国公路交通的不断发展,交通荷载逐渐重型化,加之养护工作的不及时,使得部分沥青路面已出现性能衰退、结构损伤、设计荷载标准低等现象,仅仅通过小修工程难以达到规定的道路服务水平,若继续放任通车会导致沥青路面病害逐步劣化、加速路面破坏。对旧沥青路面进行科学合理的大中修养护不仅能最大程度恢复道路的路面技术状况,还能延长沥青路面的剩余使用寿命。因此,对旧沥青路面及时采取大中修养护具有一定的必要性。
大中修养护方案的选择是沥青路面大中修工程的关键步骤,采取不同的大中修养护方案会对沥青路面的未来使用性能、养护资金利用效率、环境造成不同的影响。近年来,针对养护方案决策方法的研究也受到不少学者的关注,Christina等[1]考虑了路面养护对生态环境的影响,采用生命周期评估(life cycle assessment,LCA)对不同养护方案的进行环境的量化分析;Ji等[2]提出了一种基于马尔可夫链和粒子群优化的综合方法,从路面使用性能角度确定最佳养护策略;Torres-Mzchi等[3]考虑经济和环境指标以及相关次级指标,运用层次分析法和优选法分别对4种不同养护方案进行分析;Shi等[4]基于路面技术状况指标和养护费用,采用二次规划和遗传算法建立了多目标优化决策模型。
上述学者在进行方案决策时,虽然都考虑了不同的目标,但往往只考虑经济、环境或使用性能单方面的影响,或以其中两方面为重,没有将经济、环境和使用性能三方面统筹兼顾。同时,在解决多目标且存在相互矛盾关系的决策方法中,多个目标很难同时达到最优,不同目标之间也存在相互制衡的关系。因此,大中修养护方案决策问题可作为复杂的多目标优化问题进行求解。常用的多目标优化方法有粒子群算法、模拟退火算法、非支配排序算法等。其中非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)以其运算时间短、种群具有多样性的特点被广泛应用,但单一的搜索策略使其面对高维数据集时极易陷入局部最优解,导致收敛结果不够理想。基于参考点的非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅲ,NSGA-Ⅲ)通过引入参考点的方法构造超平面,可以解决高维多目标、具有非支配关系的多目标优化问题,2014年由Deb[5]首次提出,并已在储能系统优化[6]、船舶配载规划[7]等领域得到了广泛研究。TOPSIS(technique for order preference by similarity to ideal solution)作为一种多属性决策方法,通过计算各个方案与理想解的距离得到不同的综合评价指标,可用于Pareto解集的前端曲线分析及决策。但TOPSIS法容易产生同时逼近正负理想解、无法解决协方差矩阵为0或不可逆时计算无法进行、数据量过大导致数据灾难等缺陷。
鉴于此,现基于实现沥青路面大中修养护低污染、低成本、高质量的理念,建立以碳排放量、寿命周期成本以及路面使用性能为目标函数的多目标优化模型,并采用广义马氏距离组合赋权的TOPSIS法对所有最优解集中的方案进行优级排序并决策,最后通过实际项目进行优化示例演示,为可持续性的沥青路面大中修养护方案决策提供科学合理的理论参考。
1 沥青路面大中修养护方案模型
1.1 假设条件
模型的构建主要基于以下假设条件:①进行大中修的路段具有相同的地质、水文、气候;②不考虑其他外界因素影响下对养护方案及施工进度的影响;③结构层厚度满足路面标高要求,且不考虑增加其他交通附属设施。
1.2 数学模型
建立沥青路面大中修养护方案多目标优化模型,即
Z=min{Z1,Z2,-Z3}
(1)
式(1)中:Z为整体优化目标;Z1、Z2、Z3为子目标函数,分别代表大中修养护的碳排放量、寿命周期成本以及路面使用性能。
1.2.1 碳排放量模型
通过对实际工程施工现场的碳源追溯,将大中修养护工程划分为路面养护技术、沥青混合料的生产和沥青混合料施工3个阶段。其中路面养护技术依据《公路沥青路面养护设计规范》(JTG 5421-2018)[8]附录B最常用的养护对策,划分为直接加铺补强、面层铣刨重铺以及路基路面结构重建3部分;沥青混合料的生产依据文献[9]划分为集料堆料、集料干燥、沥青加热、混合料拌合4部分;沥青混合料施工划分为沥青混合料的运输、摊铺以及碾压3个部分[10]。沥青路面施工的碳排放来源为柴油、重油、原煤、电力、天然气。大中修养护中沥青混合料生产工艺及碳排放情况如图1所示。
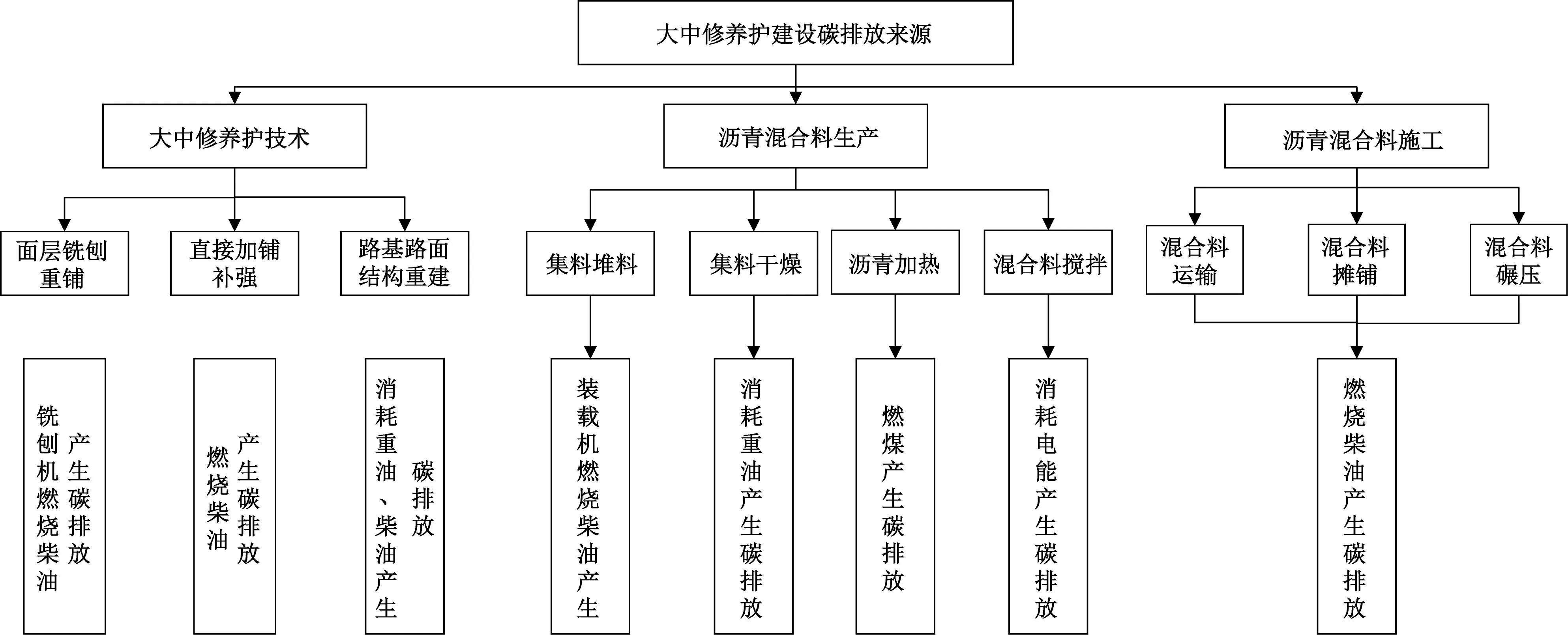
图1 大中修养护碳排放追溯Fig.1 Carbon emission tracing ofmedium and heavy maintenance
大中修养护各施工环节使用的能源类型和能耗量化存在差异,因此,必须明确碳排放计算参数才能建立大中修养护过程中的能耗碳排放模型。本文研究采用联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)和国家统计局提供的碳排放因子、能源热值Q和全球增温潜势值(global warming potential,GWP)为能耗和碳排放的计算参数[11-12]。IPCC在2019年的修订报告中显示,造成温室效应的气体主要包括CO2、CH4、N2O、SF6、HFCS等,而在沥青路面养护施工过程中,CO2、CH4、N2O所占比例较大,其他温室气体排放量较小,因此选择这3种气体为主要对象进行研究。
在碳排放模型中,温室气体的排放量统一单位为当量碳排放量(CO2eq),不同的温室气体有不同的全球变暖潜值,其中CO2、CH4、N2O的全球变暖潜值分别为1、28、265[13]。采用国家统计局提供的能耗碳排放因子作为沥青路面养护过程中的碳排放因子,如表1所示。依据能源燃烧特点及全球变暖潜值,得到在大中修过程中碳排放量最小化模型为

表1 能耗碳排放因子Table 1 Energy consumption carbon emission factor
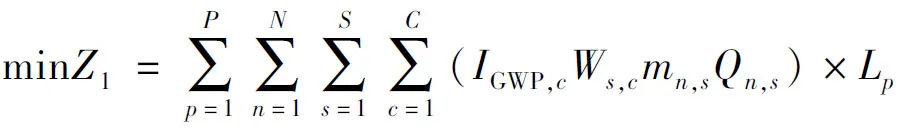
(2)
式(2)中:p为需要进行大中修的路段;P为大中修路段数,且p∈P;n为大中修的备选方案;N为大中修备选方案数,且n∈N;s为施工环节,包括集料堆料、集料干燥、沥青加热、沥青混合料拌合、运输、摊铺、碾压,且s∈S;c为温室气体的类型,分别为CO2、CH4、N2O,且c∈C;IGWP,c为不同温室气体的全球变暖潜值;Ws,c为在s阶段所产生的温室气体的碳排放因子;mn,s为第n种养护方案在不同施工环节的单位能源消耗量;Qn,s为第n种养护方案在不同施工环节的能源热值;Lp为不同路段的长度。
表2给出了不同燃料的能源热值。

表2 能耗碳排放因子Table 2 Energy calorific value of each fuel
1.2.2 寿命周期成本模型
寿命周期成本分析法在道路行业已有较为广泛的应用,依据《公路沥青路面养护设计规范》(JTG 5421-2018)可知,路面全寿命周期成本包括管养部门费用和道路使用者费用两部分。管养部门费用指的是从开始施工到项目结束的整个费用,项目的预算比较全面地概括了每种方案在建设中的整个费用,因此不需要繁琐的计算。道路使用者费用主要包括车辆运行费用,本文研究采用燃油消耗模型来计算寿命周期成本中的车辆运行费用[14]。因此寿命周期成本最小化模型为
minZ2=AC+UC
(3)
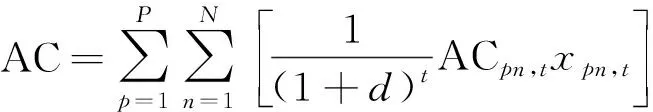
(4)

(5)
式中:AC为路面管养费用;UC为道路使用者费用;d为贴现率,本文取4%;ACpn,t为路段p采取养护措施n时在路段设计年限t年内的路面管养费用;UCpn,t为路段p采取养护措施n时在设计年限t年内的道路使用者费用;xpn,t为当路段p在第t年采取养护措施n时等于1,否则xpn,t等于0。
依据项目观测站-西破庙观测站(观测站编号为 S244L271130826)所调查的交通量,通过分析交通调查结果将车辆划分为中小客车、大客车、小货车、中货车、大货车、特大货车、集装箱7种类型。则车辆t年后的道路使用者费用为
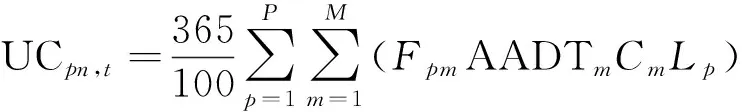
(6)
Fp=a+bv+cv2
(7)
式中:Fpm为第m种车型的百公里油耗;AADTm为第m种车型的年平均日交通量;Cm为第m种车型的燃油单价;Lp为路段p的长度;a~c为模型系数;v为车辆平均速度。
表3为油耗模型各参数值。

表3 油耗模型参数Table 3 Fuelconsumption model parameters
1.2.3 路面使用性能模型
路面使用性能能真实地反映不同道路的基本情况和使用性能的发展趋势,对路面使用性能进行预测可以有效帮助管理部门选择较好的养护方案。路面养护维修后的使用性能衰变,因其所处路面管理系统等级的不同,导致其量测具有不同的指标。在项目级路面管理系统中,对养护维修后的使用性能衰变可以采用某项路面破损程度(如裂缝率、车辙深度等)进行量化;或运用路面功能性降低的程度(如平整度指数、横向力系数等)进行评价;或表现在路面使用性能评价值的降低幅度[15]。选取路面损坏状况指数PCI作为路面使用性能评价指标,采用孙立军的路面行驶质量衰变模型[16],因此路面使用性能最大化模型为
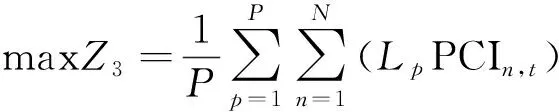
(8)
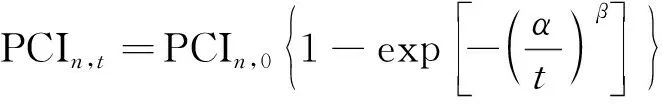
(9)
式中:Lp为需要进行大中修路段的长度;PCIn,t为采用不同养护方案在分析年限第t年的PCI值;PCIn,0为采用不同养护方案时新建路面初始PCI值,这里取值均为100;α、β为方程回归参数。
1.3 约束条件
约束条件即为模型中所有可能的限制条件,即

(10)
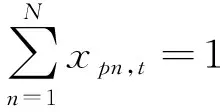
(11)
75≤PCIt≤100
(12)
式中:Bt为公路养护管理部门的预算。式(10)表示养护管理部门的经费预算限制;式(11)表示该路段在分析期内只进行一次大中修;式(12)表示《公路沥青路面养护技术规范》(JTG 5142-2019)[17]中规定的路面损坏状况指数的养护阈值,即低于该阈值时需进行养护维修。
2 模型求解方法
2.1 基于NSGA-Ⅲ算法的模型求解方法
采用NSGA-Ⅲ算法对沥青路面大中修养护方案进行优化,相比于传统的层次分析法对大中修养护方案进行决策,本文的NSGA-Ⅲ算法有以下优点。
(1)科学性强。层次分析法的定量指标少,定性指标多,缺少相关的数学论证,科学准确性较差,不易令人信服。而NSGA-Ⅲ算法可将每个目标的数值准确计算出来,可较为直观地看出不同方案的差异性。
(2)计算准确迅速。层次分析法在指标较多的情况下,需进行多次的两两判断矩阵比较,并进行一致性检验,计算量复杂且庞大。采用本文所述方法只需将数值输入程序中,在较短的时间内即可得出计算结果,省去大量人工计算。
(3)解决指标间的差异性。层次分析法并未对指标间存在的关系进行分析,有的指标间存在此消彼长的矛盾关系,单纯地赋值并不能得到最优的方案,NSGA-Ⅲ算法可以有效解决不同目标间的非支配关系,排除这一隐患。
NSGA-Ⅲ算法通过参考点机制保持种群的多样性[18],而归一化操作是参考点机制的核心[19]。图2为模型求解流程图,详细步骤如下。
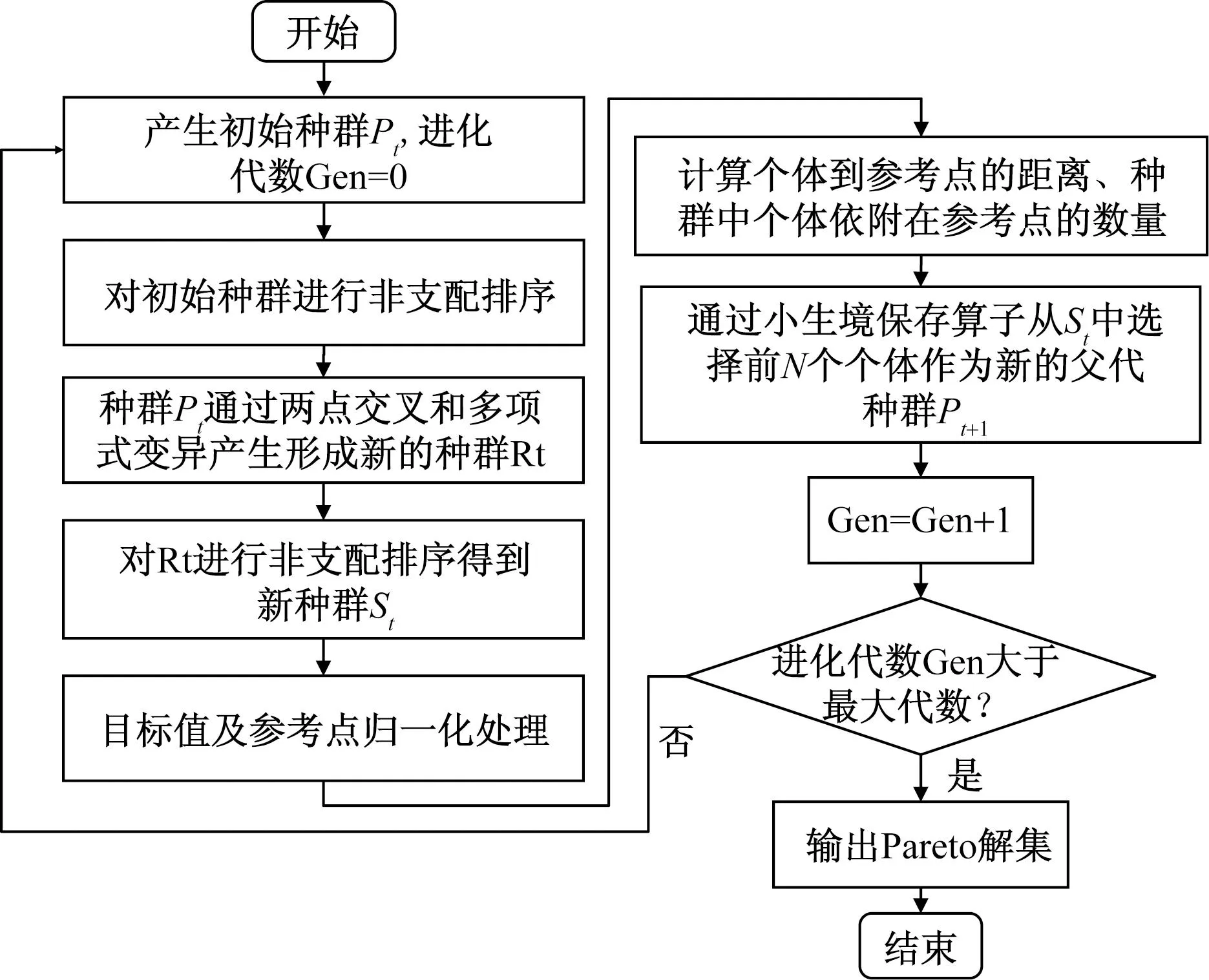
图2 模型求解流程图Fig.2 Flow chart of modelsolving
(1)设置全局变量,初始化路面决策参数。输入不同路段大中修养护长度、交通量等参数,初始化超平面参考点。
(2)采用连续实数编码方式进行编码,生成含有N个个体的初始种群Pt。
(3)对初始种群进行非支配排序,通过两点交叉和多项式变异产生种群大小为N的子代Qt,形成新的种群Rt=Pt∪Qt,然后经过非支配排序,将非支配层的解加入新建的种群St中,直到St种群的大小大于或者首次大于N时迭代停止。

f′i(x)=fi(x)-Zimin
(13)
计算极值点,通过量化函数计算第i维目标的极值点为
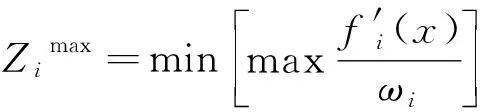
(14)
式(14)中:ωi=(ε,ε,…,ωi,i,…,ε),其中ε=10-6,ωi,i=1。
③构建线性超平面,通用方程为
Λ1x1+Λ2x2+…+Λixi=1
(15)
式(15)中:Λ1~Λi为不全为0的常数;x1~xi为超平面上任意一点坐标。
④种群目标归一化,表达式为
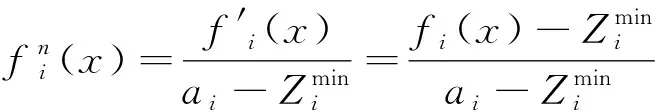
(16)
(5)通过小生境保存算子从St中选择前N个个体作为新的父代种群Pt+1。
(6)判断进化代数Gen是否达到最大迭代数,若达到条件即可输出Pareto最优解集,如果没有达到则继续循环。
2.2 基于广义马氏距离组合赋权的TOPSIS法
传统的TOPSIS法通过欧式距离计算综合评价指标,但欧式距离难以排除各目标间量纲不同而产生的干扰性[20],马氏距离(Mahalanobis distance)[21]很好地解决了这个问题。由于在马氏距离公式中的协方差矩阵必须满秩,因此具体计算步骤如下。

A=(aij)p×q=(ξjnij)p×q
(17)
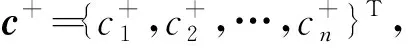
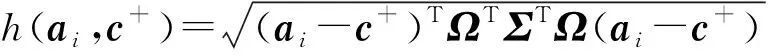
(18)
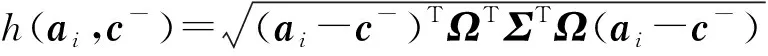
(19)
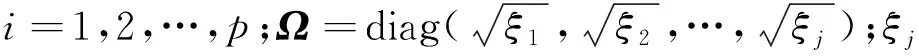
若协方差Σ行列式等于0或者为奇异矩阵时,Σ-1不存在,则用伪逆矩阵Σ+代替逆矩阵,伪逆矩阵的求解方法如下:将Σ进行奇异值分解Σ=USV′,则Σ+=VTU′,其中S=diag(a1,a2,…,ar),r为矩阵的秩,U、V为正交矩阵,且当S(i,j)=0时,T(i,j)=0;当S(i,j)≠0时,T(i,j)=1/S(i,j)。
最后计算各方案的综合评价指标λi,λi=h(ai,c+)/h(ai,c+)+h(ai,c-),为Pareto解集中所有备选方案与理想点与负理想点的距离,λi越大,说明该方案越贴近于选择标准即最佳决策方案。
3 实例分析与讨论
3.1 旧路调查与分析
省道半虎线承德段起点为丰宁县张家口交界,终点为虎什哈镇火车站,起讫点桩号为K91+283至K262+668,路线全长207.385 km。全线为二级公路,路线贯穿承德市丰宁县和滦平县,省道半虎线是承德市西南部地区与张家口地区政治经济交往的重要公路。对承德市省道半虎线进行路面历史信息调查以及路面状况调查,钻芯取样结果表明病害已发展至基层,面层与基层脱离,存在基层、面层结构松散破坏等问题,路面损坏状况指数PCI=60.8,已达到中、差等级。依据《公路沥青路面养护设计规范》(JTG 5142-2019)可以得出以上路段需进行修复养护,并给出3种备选方案:①铣刨加铺;②直接加铺;③全深式泡沫沥青冷再生,并依据规范中给出二级公路大中修设计年限范围,确定路段的设计年限为5年。表4给出需要进行修复路段的起讫里程及原路面结构。
根据现场调查以及路面状况分析,参考相关规范及往年修复养护工程经验,列举3种不同养护方案,如表5所示,并给出具体处治措施。
模型中不同路段的主要设计决策变量取值如表6所示,PCI衰变方程模型参数通过省道半虎线在2017-2019年的养护历史及使用性能检测数据来确定,利用nlinfit法在表7给出了适用于不同养护方案的回归参数值。
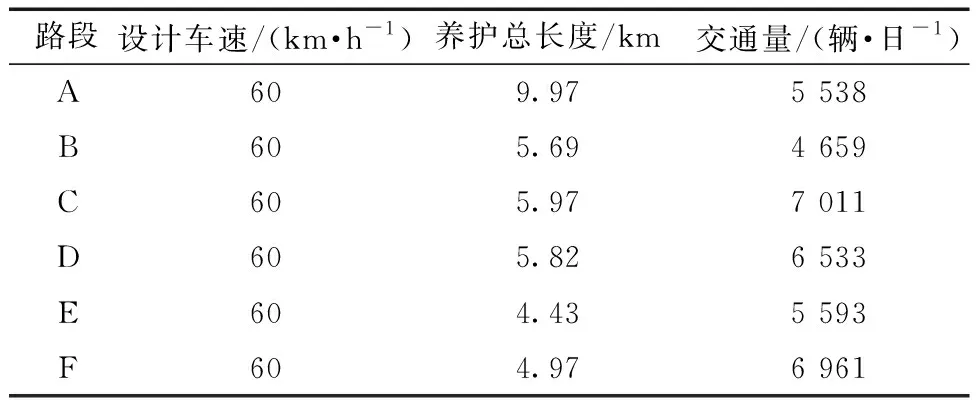
表6 不同路段变量取值Table 6 Values of variables for different road sections
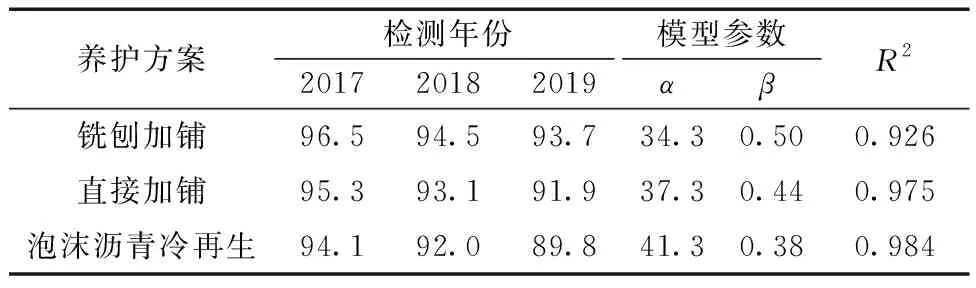
表7 不同养护方案PCI衰变方程模型参数Table 7 PCI decay equation model parameters for differentmaintenance scheme
3.2 计算结果分析
模型初始参数设置如下:初始种群数量N=400;最大迭代次数为500;交叉概率为0.9,变异概率为0.01,得到290个Pareto解,最优解集如图3所示。

图3 最优化Pareto解集Fig.3 Optimal Pareto solution set
理想解是TOPSIS法中的一种虚构解,多用于求解多目标优化模型[22]。假定Pareto解集中任意一点为理想解I,通过MATLAB计算Pareto解集中所有点与理想解的相对马氏距离,运行后得到综合评价指标,组合赋权值如表8所示。输入sort函数,即可得到最优养护方案决策,如图3中O点所示。表9是综合指标排序前五的方案。

表8 不同目标的主观权重与客观权重Table 8 Subjective weights and objective weights of different objectives

表9 综合指标评价排序前五Table 9 Comprehensive index evaluation ranking top five
如果考虑方案的寿命周期成本和路面使用性能双目标的话,则最优解为图3中S所示;如果只考虑成本一个目标的话,则最优解为图3中C所示。各项方案对比可知,方案O比方案S的碳排放量降低24.45%,寿命周期成本降低14.4%,PCI降低1.07%;方案O比方案C的碳排放量降低28.4%,寿命周期成本降低17.95%,PCI降低3.68%。
由表8和表9的结果可知,当主观赋权值相同时,泡沫沥青冷再生方案为较优选择,这是因为泡沫沥青冷再生技术不仅将废弃的沥青材料进行循环利用,降低原材料的成本,同时在施工的过程中不需要加热沥青,减少了大量的碳排放以及空气污染。
3.3 权重敏感性分析
由于TOPSIS法中权重的变化对最优解有一定的影响,采用敏感性分析来确定不同目标变化时对目标值的影响程度。文献[3]提出一种将权重等级划分为较重要、重要和次重要的方法,即将权重值分别对应赋值为0.5、0.3、0.2,并列举6种不同的权重策略,分析其对最优解的影响。表10为6种不同策略对应的权重值,其中策略1和策略2中PCI均值的权重等级为较重要,策略3和策略4中寿命周期成本的权重等级为较重要,策略5和策略6中碳排放量的权重等级为较重要。
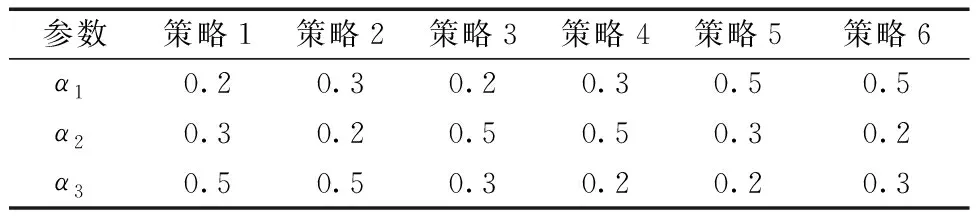
表10 不同策略对应权重Table 10 Corresponding weights of different strategies
将上述给出的权重与客观权重耦合后,在TOPSIS主程序中输入不同权重值,即可得到不同的综合评价指标以及最优解,结果如图4和图5所示。对比图4中的结果可知,当碳排放量的权重等级为较重要时,A~F路段中选择泡沫沥青冷再生方案的占比较多;当寿命周期成本的权重等级为较重要时,A~F路段中选择3种方案的均有;当PCI的权重等级较重要时,A~F路段中选择铣刨加铺方案的占绝大多数。这可能是因为泡沫沥青冷再生方案的施工过程中碳排放量少于其他两种方案,对环境较为友好;而铣刨加铺作为较为传统的加铺方式,在沥青路面服役期间的长期使用性能上相比于其他两种方案表现良好;由于寿命周期成本受多方面因素影响,包括不同车型的交通量、百公里油耗等,因此当寿命周期成本的权重等级较重要时,方案的选择没有一定规律性。
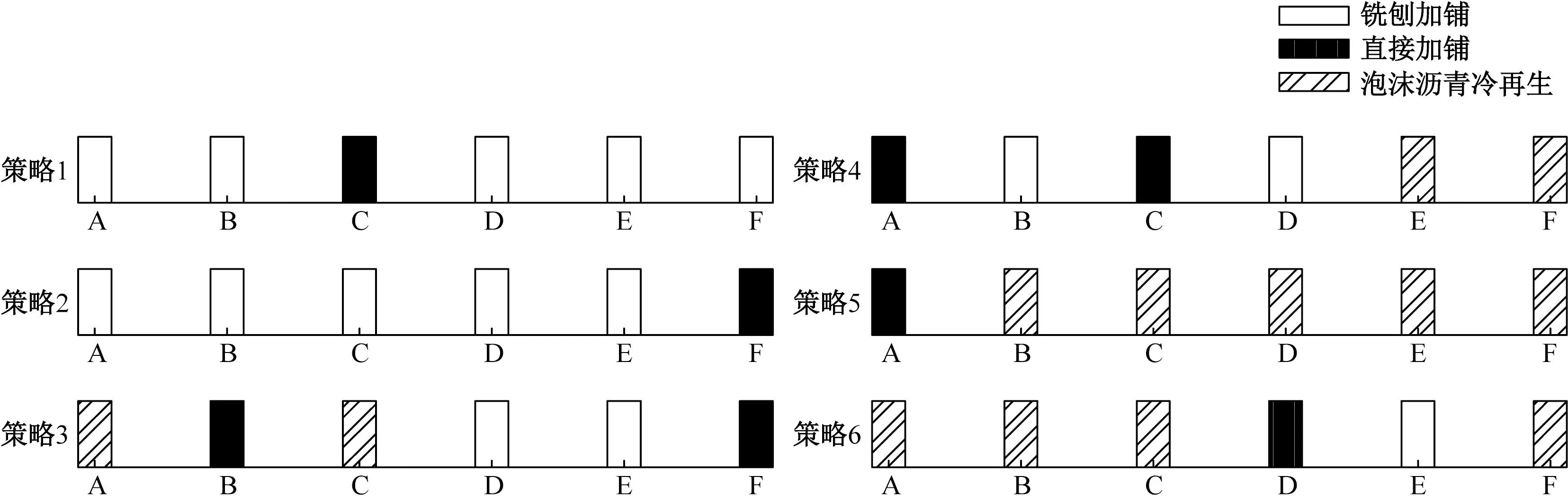
图4 不同权重等级的养护方案最优解Fig.4 Optimal solution of the conservation scheme with different weighting levels
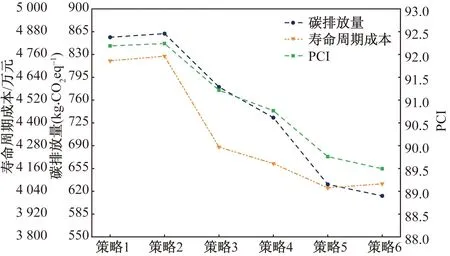
图5 不同权重等级目标值Fig.5 Target values for different weight classes
由图5中的结果可知,策略1和策略2的PCI值最高,但碳排放量和寿命周期成本也很高;策略5和策略6的碳排放量和寿命周期成本最低,但PCI值相比于其他策略较低。
由此可见,在客观权重一定的情况下,目标的主观权重越大,则最优方案在该目标的优化效果越好,而对其他决策目标的优化效果变差。
4 结论
针对干线公路沥青路面大中修养护工程中碳排放量较大、寿命周期成本高等问题,采用NSGA-Ⅲ算法和广义马氏距离组合赋权的TOPSIS法,提出了一种优化方法对养护方案进行决策,使得方案决策更趋科学、合理,得出如下结论。
(1)以碳排放量、寿命周期成本和路面使用性能为目标,建立了沥青路面大中修养护决策多目标优化模型,依据承德市干线公路的实际状况,采用NSGA-Ⅲ算法对模型进行求解,得到了Pareto最优解集。
(2)通过广义马氏距离组合赋权的TOPSIS法计算并比较Pareto解集中所有方案的综合评价指标,按照优级排序对前五种方案进行分析,发现相比于只考虑单目标和双目标的方案,选择出的最优方案在碳排放量上明显降低。
(3)对比传统的层次分析法和NSGA-Ⅲ算法,总结了采用NSGA-Ⅲ算法的3条优点,即科学性强、计算迅速准确和指标间的差异性问题。
(4)考虑主观赋权中权重值的敏感性,分析不同赋权值对养护方案最优解以及目标值的影响,结果发现不同的权重等级下PCI值、碳排放量及寿命周期成本不同,且在客观权重一定的情况下,目标主观权重越大,最优方案在该目标的优化效果越好,而对其他决策目标的优化效果变差。
