地铁扣件Ⅲ型弹条的弹塑性疲劳性能分析

2024-01-12陈金明钟盛华彭睿刘逸平韦志坚傅忆宾

科学技术与工程 2023年34期

陈金明, 钟盛华, 彭睿, 刘逸平*, 韦志坚, 傅忆宾

(1.广州计量检测技术研究院, 广州 510663; 2.华南理工大学土木与交通学院, 广州 510641)

扣件系统是轨道结构的重要组成部分,主要是通过弹条变形产生的扣压力来紧固铁轨,同时达到减振的作用。弹条在设计年限内要求不允许出现失效[1],然而在现实服役过程中,扣件系统往往未达到设计标准就发生损坏,尤其是弹条部件,给列车行车安全带来了巨大隐患。因此,对弹条失效问题的研究是非常必要的。

目前中外学者针对铁路扣件系统失效的研究已有了许多成果。尚红霞等[2]分析了地铁扣件Ⅲ型弹条在不同安装状态下的应力状态,建议为避免因产生接触应力集中而发生破坏,弹条后拱小圆弧内侧与铁垫板的距离应控制在8 ～ 10 mm。 Gao等[3]对W1型弹条失效问题进行了研究,认为列车高速运行时轮轨力提高了弹条应力是原因之一,并提出了一种高阻尼复合弹条来提高弹条的使用寿命。刘艳等[4]通过弹条材料应变-寿命曲线,对W300-1型扣件弹条进行了寿命预测与分析,发现弹条疲劳寿命与危险点应力比呈线性关系,建议弹条安装时安装扭矩不超过300 N·m。Xiao等[5]通过对e型弹条的有限元分析,并结合现场弹条振动试验,发现钢轨波磨引起弹条共振是弹条断裂的原因之一。薄栋乾等[6]研究了Ⅲ型弹条的受载特征对其疲劳损伤的影响,发现弹条在钢轨波磨条件下的疲劳损伤发生在弹条后拱靠近跟端处,且曲线波磨条件下的疲劳损伤大于直线波磨条件的情况。 Zhang等[7]对一个60Si2Mn材料弹条的异常断裂进行了研究,并结合有限元分析进行了对比,发现断裂位置与最大应力位置不相符,认为弹条的异常断裂是因裂纹开始时存在锈蚀引起的。外界环境因素导致失效的情况也可能存在,建议对弹条进行严格的防腐处理。Anat 等[8]采用有限元对e型弹条的应力进行了数值计算,并结合疲劳试验结果进一步对弹条进行了疲劳分析,指出车轮冲击荷载作用时弹条的疲劳寿命大大降低。余剑等[9]开展了W1型弹条的静力电阻应变测试和疲劳试验,发现合适的扣压力能有效保证弹条的疲劳寿命,且随着疲劳循环次数的增加,扣压力与弹条中端圆弧位移存在相关性。

已有对e型弹条疲劳寿命的研究多为单轴分析,然而在实际中处于多轴应力状态。因此,现针对地铁Ⅲ型扣件系统建立有限元模型,进行静力学分析,并在此基础上对弹条进行弹塑性疲劳性能研究,预测弹条的疲劳寿命及损伤演化规律。

1 数值模拟

1.1 有限元模型的建立

地铁Ⅲ型扣件系统由Ⅲ型弹条、铁垫板、板下垫板、绝缘轨距块、钢轨、轨下垫板等组成。扣件系统在实际使用中通过弹条趾端变形产生的扣压力来紧固铁轨。考虑到几何模型的复杂性,为提高计算效率,本文研究对地铁Ⅲ型扣件系统进行了简化。使用建模软件SOLIDWORKS以及有限元软件ABAQUS建立了扣件系统的局部有限元模型,模型中包含了Ⅲ型弹条、局部铁垫板以及简化轨距块,如图1所示。在此模型的网格划分中,弹条采用5 639个六面体单元(C3D8R)以及7 593个四面体单元(C3D10),铁垫板采用11 649个四面体单元(C3D10),简化轨距块采用190个线性四边形单元(R3D4)。

图1 扣件系统有限元模型Fig.1 Finite element model of the fastener system

1.1.1 材料属性

弹条的材料为60Si2Mn弹簧钢,根据力学性能标准[10]规定,屈服强度应不低于1 375 MPa,抗拉强度不低于1 570 MPa,考虑材料的弹塑性,本构采用理想线性强化弹塑性模型,强化模量E1=0.1E[6],其中,E为弹性模量,如图2所示。由于轨距块的材质对计算结果影响较小,为方便后续扣压力的计算,这里将其定义为离散刚体。模型所用材料参数如表1所示。

表1 材料参数Table 1 Material parameter

图2 理想线性强化弹塑性模型Fig.2 Ideal linear strengthen elastoplastic model

1.1.2 边界条件与载荷

由于地铁Ⅲ型扣件系统在工作时,各部件之间存在接触,本文研究采用非线性接触理论定义各部件之间的接触关系[2],在局部有限元模型中,设置了3个接触对,分别是弹条跟端与铁垫板承台,弹条中肢与铁垫板插孔,轨距块上表面与弹条趾端下表面,如图1所示。接触类型均为表面与表面接触,其中法向为硬接触,不允许接触对之间产生穿透行为。切向存在摩擦力,采用罚函数定义,各接触对之间的摩擦系数均为0.3,如表2所示。为了模拟扣件系统在工作时的受力状态,对铁垫板底部设置全约束,通过对轨距块施加垂向位移来实施加载。

表2 接触关系Table 2 Contact relation

1.2 结果分析

根据文献[2],为了保证弹条的安装符合设计要求,避免弹条在服役过程因长时间发生接触应力集中而失效,弹条后拱小圆弧内侧与铁垫板距离D(图3)的数值应适当选择。

图3 小圆弧内侧与铁垫板的距离DFig.3 The distance D between the inner side of the small arc and the iron backing plate

为选取合适的距离D研究弹条的力学性能,本文研究建立了不同D值的有限元模型,对轨距块施加13 mm垂向位移荷载并进行了结果分析对比,图4为接触应力与距离D之间的关系,图5为弹条接触区域随D的变化。

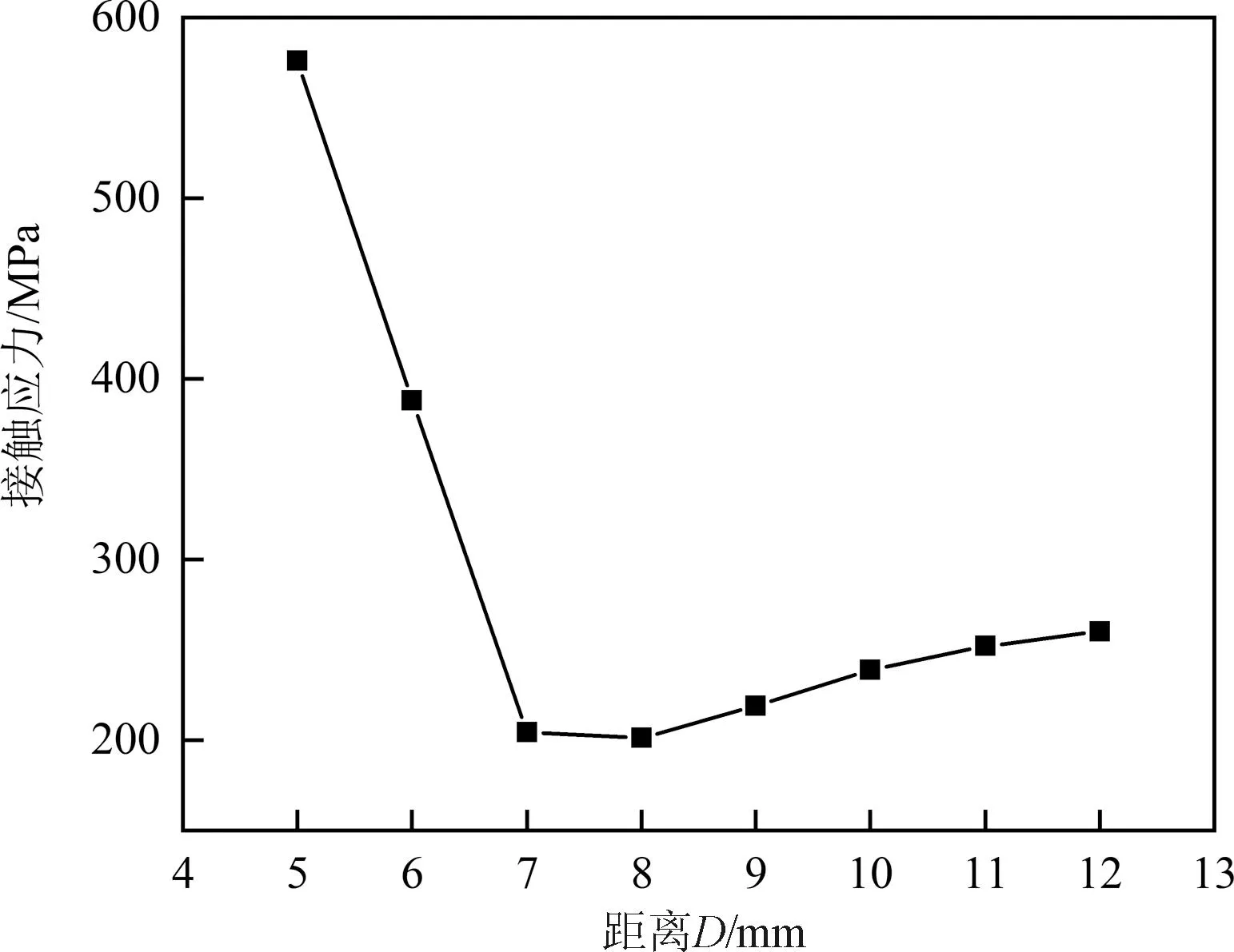
图4 接触应力与距离D的关系Fig.4 Relation between contact stress and distance D

图5 弹条与铁垫板接触区域随D的变化Fig.5 Variation of the contact area between clip and iron pad with D

由图4可知,当D<7 mm时,接触应力随着D的减小显著增大,同时结合图5可发现,随着D的数值从8 mm减小至6 mm,接触区域也由线接触逐渐变成多点接触。为了避免弹条因接触区域变小而产生应力集中,弹条后拱小圆弧内侧与铁垫板距离应不得小于7 mm。

当弹条未发生明显的接触应力集中时,各工况下弹条的最大应力以及扣压力均相差很小,结合文献[2]提出的D的合适范围为8～10 mm,为方便计算,本文后续的计算工况均采用D=10 mm,即弹条后拱小圆弧段未插入铁垫板插孔内。

1.3 模型验证

考虑到Ⅲ型弹条的材料60Si2Mn弹簧钢是典型的塑性材料,可采用第三和第四强度理论,由于弹条在服役时处于复杂的应力状态下,而第三强度理论未考虑第二主应力的影响,本文研究采用第四强度理论(Mises屈服准则)作为评价指标对弹条进行分析,即在一定的变形条件下,某点的等效应力达到屈服点时,该点就开始进入塑性状态,可以表述为

(1)

为分析弹条在服役时的应力状态,提取弹程Δ=13 mm工况时的Mises应力与扣压力F,其中以弹条趾端中点的竖直位移作为弹程,以轨距块竖直方向的反作用力作为扣压力。Mises应力与扣压力关系如图6所示。

图6 最大Mises应力与扣压力关系Fig.6 Relation between Maximum mises stress and the clamping force

由图6可知,扣压力F=10.82 kN时弹条开始局部进入屈服阶段(≥1 375 MPa),此时对应的弹程为10.49 mm。弹程为13 mm时,弹条产生的扣压力为13.3 kN,满足扣压力大于11 kN的标准[11]。

图7为此模型下线弹性状态时的扣压力与弹程关系。由图7可知弹条扣压力与弹程的关系可视为是线性的,即

图7 扣压力与弹程关系Fig.7 Relation between clamping force and displacement

F=KΔ

(2)

式(2)中:F为扣压力,kN;Δ为弹程,mm;K为弹性系数,kN/mm。

对试验数据点进行直线拟合,可得弹条的弹性系数K为1.06 kN/mm。与文献[2]结果较为吻合,认为该模型是具有可行性的。

1.4 弹条在不同工况下的应力应变状态

为研究弹条在不同弹程或扣压力下的应力应变状态变化,对弹程11 mm和13 mm工况进行结果对比分析。由图8和图9可知,当弹程为11 mm时最大应力发生在弹条后拱小圆弧,此时部分区域开始进入屈服,局部最大Mises应力为1 389 MPa,最大等效塑性应变(PEEQ)为6.744×10-4。而随着弹程增大到13 mm时,弹条的局部最大应力达到了1 441 MPa,并且出现了两个应力集中区域,分别为后拱小圆弧、跟端与大圆弧连接处,如图8(b)所示,此时最大等效塑性应变(PEEQ)明显增大,达到了2.858×10-3,且其进入塑性屈服的区域也明显扩大,如图9(b)所示。

图8 Mises应力云图Fig.8 Nephogram of Mises stress

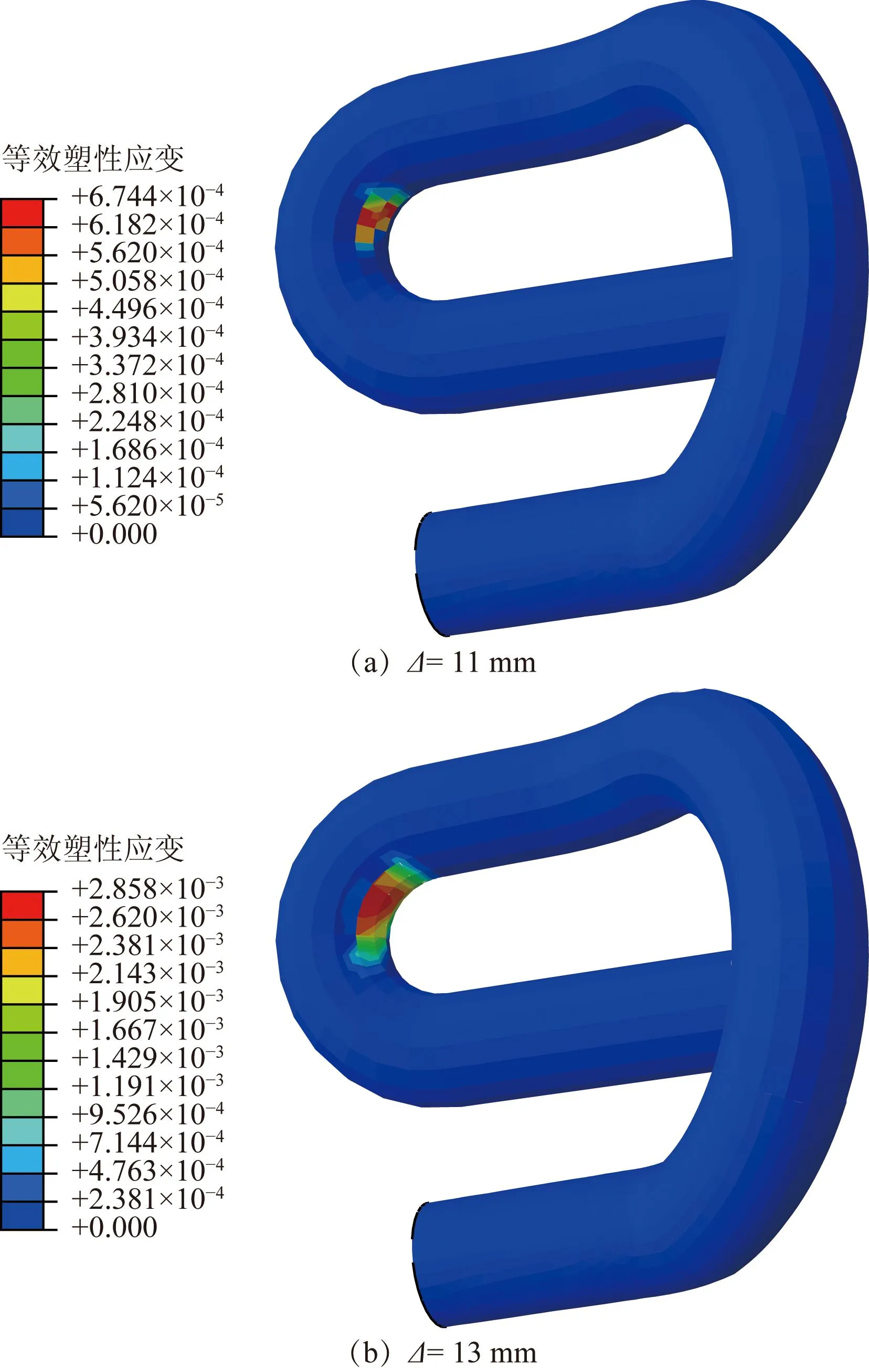
图9 等效塑性应变云图Fig.9 Nephogram of equivalent plastic strain

2 弹塑性疲劳性能分析

列车在行进过程中会对钢轨产生垂直方向的振动位移,扣件系统在长期的疲劳荷载作用下发生疲劳损伤,近年来,随着地铁运力的提高,弹条断裂的情况时有发生,为分析弹条的疲劳性能,前文确定了弹条在服役工况下的应力应变状态。由于弹条在弹程13 mm安装状态下局部区域已进入塑性,故采用弹塑性疲劳分析的方法对弹条的疲劳性能展开研究。本文研究建立了两种弹塑性疲劳模型,其中模型1采用Neuber准则[12]塑性修正的弹性有限元法,模型2采用弹塑性有限元法。

将有限元计算得到的荷载谱导入Fe-safe中,由于60Si2Mn弹簧钢为延展性较好的材料,故本文研究使用经过Morrow平均应力[13]修正的Brown Miller应变寿命曲线[14],以及Palmgren-Miner线性累积损伤理论[15]对两个模型下的弹条疲劳寿命进行分析。

2.1 疲劳计算相关理论

(1)Neuber公式。材料处于弹性阶段时,应力应变呈线性关系,当应力开始进入屈服阶段时(达到σs),应力随应变的增量不再是弹性阶段的比例关系,根据Neuber公式进行塑性修正,即

(3)

式(3)中:Kt为理论应力集中系数;Kσ为真实应力集中系数;Kε为真实应变集中系数;σ、ε分别为真实应力和应变;s、e分别为名义应力和应变。

(2)循环应力-应变曲线。金属材料的应力应变滞回曲线经过一定的循环次数后趋近于封闭环,即可得到稳定的闭合线,利用在不同应变水平下的恒幅对称循环疲劳试验,可以得到材料的循环应力-应变曲线[16],由文献[16]得到60Si2Mn材料的循环应变为

(4)

式(4)中:εa为总应变幅;εea为弹性应变幅;εpa为塑性应变幅;σa为应力幅;E为弹性模量;K′为循环强度系数;n′为循环应变强化指数。

(3)Brown Miller 应变寿命方程。

(5)

式(5)中:γmax为最大剪应变;εn为正应变;ε1和ε3分别是第一和第三主应变;Δγmax为最大剪应变幅;Δεn为正应变幅;N为寿命;ε′f为疲劳延性系数;σ′f为疲劳强度系数;b为疲劳强度指数;c为疲劳延性指数。

(4)Morrow平均应力修正后的疲劳寿命方程。

1.75ε′f(2N)c

(6)

式(6)中:σm为平面上的平均正应力。

由文献[16]可知,60Si2Mn材料的循环应变特性参数如表3所示。

表3 循环应变特征参数Table 3 Characteristic parameters of Cyclic strain

(5)Palmgren-Miner线性损伤累积理论。如果构件在k个应力水平σi作用下,各经受ni次循环,线性损伤累积理论认为各个应力水平下的损伤可视为是相互独立的,总损伤可进行线性累积,且当总损伤等于1时,构件发生疲劳破坏。其定义为

(7)

式(7)中:ni为循环次数;Ni为某恒幅循环应力σi

作用下的寿命;Di为经受该应力水平ni次循环的损伤;D为累积的总损伤。

2.2 弹条在服役状态下的寿命预测

扣件系统在服役过程中,列车经过时产生轮轨力,导致钢轨出现垂向位移,根据文献[17],地铁线路中钢轨产生-1.47～+0.52 mm的振动竖直位移。

在弹条处于13 mm安装弹程工况下以正弦位移荷载的形式加载以模拟弹条的受力状况,如图10所示。

将其中一个正弦周期作为疲劳荷载谱导入Fe-safe中进行弹条寿命计算,得到了此工况下两个模型的寿命云图,如图11所示。

由图11可知,依据模型1和模型2计算得到的弹条的疲劳寿命分别为2.449×109次和6.081×108次,均大于标准500万次[18],弹条经过疲劳荷载后其寿命最低处发生在小圆弧段,与实际断裂位置相符,故该弹条的疲劳模型具有合理性。

2.3 弹条在不同工况下的寿命预测

扣件系统在实际服役时,由于各线路段的路况和列车载重及速度等因素导致钢轨位移发生变化。因此,对不同钢轨位移工况下弹条的疲劳寿命进行预测,结果如表4所示。由于模型1进行弹条疲劳计算时未考虑应力重分布,为分析危险截面应力状态对疲劳性能的影响,采用模型2提取小圆弧处危险点在疲劳荷载下的应力状态,得到应力比,如表5所示。

表5 不同工况下危险点的应力比Table 5 Stress ratio of dangerous points under different working conditions

图12为弹条在不同工况下的对数寿命曲线,由图12(a)可知,模型2的疲劳寿命预测曲线较模型1相对保守,随着钢轨位移差的增大,两种模型下弹条的疲劳寿命均急剧下降。其中当Δh由1 mm增加至2 mm,模型1的寿命下降了21.4%,模型2下降了22.1%;当Δh由2 mm增加至3 mm,模型1的寿命再次下降了15.4%,模型2下降了15.6%,而当Δh达到4 mm时,模型1的寿命下降到了583万次,已接近了标准的500万次,而模型2的寿命仅为305万次,更是略低于此标准。由此认为钢轨位移变化是影响弹条疲劳寿命的重要因素,为避免弹条发生过早破坏,钢轨位移差不宜过大,应小于4 mm。同时从应力状态角度看,此时弹条危险点处的应力比R应当大于0.6,如图12(b)所示。