滇池湖相粉土的工程性质

刘海军, 韩亮, 仉文岗,3,4*, 王新

(1.重庆大学土木工程学院, 重庆400045; 2.中国建筑西南勘察设计研究院有限公司,成都 610052;3.山地城镇建设与新技术教育部重点实验室, 重庆 400045; 4.库区环境地质灾害国家地方联合研究中心, 重庆 400045)

当前,为满足人们对美好生活和经济建设的需要,越来越多的邻湖、跨湖和湖底基础设施投入建设并使用,如武汉市沙湖大桥、昆明草海隧道、昆明高海高速等。湖相土一般属于软土,而软土通常承载力弱,性质复杂多变,给岩土工程建设带来诸多挑战[1]。因此,为保证涉湖基础设施得以安全施工和运营,有必要开展湖相土的工程性质研究。

目前湖相土的研究主要侧重于常规物理力学试验,比如一维固结试验和蠕变试验[2-3]、粒度特征分析[4]、有机质的组成和结构分析[5]以及水土特征曲线[6]等。此外,也有学者利用K-means算法对昆明湖相软土进行聚类分析[7]。岩土材料参数通常存在不确定性、多元相关性和趋势性[8],湖相土在沉积过程中,受沉积过程、沉积物来源和赋存环境的共同影响,空间变异性可能十分显著。如果在岩土工程结构的分析中合理考虑上述特性,则可以更有效地开展涉湖岩土工程结构的风险分析[9]。因此,需从变异性的角度深入探索湖相土的工程性质。

在土的分类方面,岩土工程规范要求通过颗粒粒径、塑性指数等指标对土进行分类[10]。这种分类方法在岩土工程实践中得到了广泛应用,但对于某些特殊土,该分类方法还存在一定局限。例如,按规范要求对昆明粉土的分类研究时,可能出现自相矛盾的情况[11],且同一类土的物理力学性质在三维空间中也存在不确定性。目前,土性参数的不确定性研究对上述问题考虑不足[12-13]。

本文研究的主要目标是利用聚类算法对滇池湖相土开展二级分类,从而更加细致地研究滇池湖相土的工程性质。目前中外鲜有同类研究被报道。本研究的主要思路为:在聚类分析的基础上,现从参数数据的深度趋势、统计分布特性和多元相关性三个方面对滇池湖相土的工程特性开展系统性研究,从而为涉湖岩土工程结构的可靠度分析和风险评估提供数据参考[9,12-13]。

1 研究数据

图1为技术流程。为实现这个技术方案,本文研究从一个国家重大项目工程中获取了湖相土相关的参数数据库,该工程场地位于昆明市的滇池附近(图2),覆盖49 200.78 m2的区域面积。

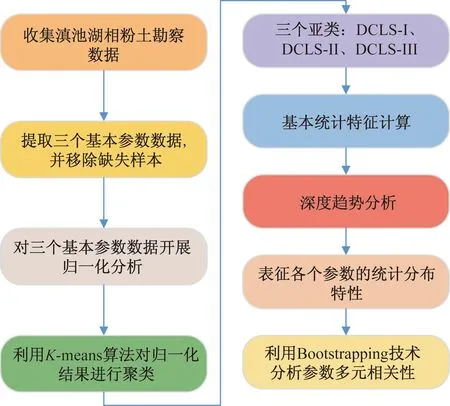
图1 技术流程图Fig.1 Flowchart in this study

图2 施工场地区域位置图Fig.2 Region of the construction site

本勘察项目的具体勘察方法和勘察要求如下。

(1)钻探方面。采用国产XY-150型钻机,以泥浆护壁和免工具拆卸(special direct,SD)系列钻具(单动岩芯管、合金钻头)回转钻进工艺,对上部土层采用套管跟管、无泵正循环回转钻进工艺进行取样。

(2)勘探深度方面。根据拟建建筑荷载及地质情况,超高层建筑区域的一般性钻孔和控制性孔的设计孔深分别为120.00 m和140.0 m;商业建筑区域分别为80.00 m和90.00 m;纯地下室区域分别为60.00 m和65.00 m;基坑外排孔深为60.00 m。

(3)取样方面。采用薄壁取土器取样,将取土器击入或静压贯入试验土层中40 cm进行取样。

根据上述要求,本项目包含57个有效钻孔,钻探深度一般大于100 m,由此获取了695个土样的试验数据样本。参照相关研究[12-13],本文研究主要选取先期固结应力Pc、黏聚力c、内摩擦角φ和有效应力σ′等16个土性参数开展不确定性分析。有效应力和先期固结应力分别以σ′/Pa和Pc/Pa的形式表示,其中Pa代表一个标准大气压,数值为101.3 kPa;c和φ由快剪试验方法获取;所有参数的相关试验方法按照《土工试验方法标准(GB/T 50123-2019)》[14]执行。

为探究滇池湖相土的工程性质,首先利用规范《土的工程分类标准(GB/T 50145-2007)》[10]中规定的塑性图识别土的类别(图3)。从图3可知,本文研究中的绝大部分土样属于高液限粉土、少部分属于低液限黏土和低液限粉土。尽管如此,常规粉土的研究结论并不完全适用于本湖相粉土[15-17],因为湖相土在赋存环境和土颗粒的微观结构方面均有其特殊性。从赋存环境来看,由于邻近滇池,本湖相土中地下水位较高,平均位于地表以下0.5 m;从微观结构来看,湖相土在沉积作用下通常以分散结构为主,各向异性明显[2]。

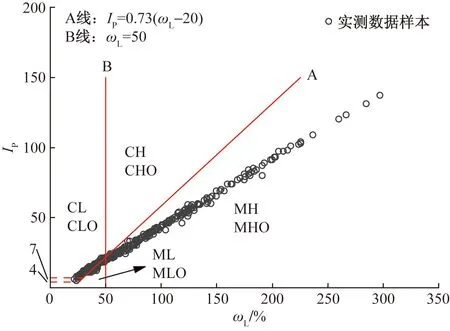
图3 塑性图Fig.3 Plasticity diagram

2 聚类分析

2.1 数据归一化

为消除特征之间的量纲差异,同时又反映特征内部的样本差异,通过最大-最小归一化方法将各特征数据样本归一化到[-1, 1]范围内,计算公式为

(1)

式(1)中:z为样本值;zmin、zmax和z′分别为样本数据的最小值、最大值和归一化值。

2.2 K-means聚类分析基本理论

受相关研究[3, 7]启发,本文研究采用K-means聚类分析开展土体样本的二级分类,其中样本间的距离采用欧式距离,即

(2)

式(2)中:xi和xj分别为多维空间中两个数据样本点,其中xi=[xi1,xi2,…,xim]T,xj=[xj1,xj2,…,xjm]T;m为数据的维度,选取三个基本参数数据作为聚类数据样本,所以本文中m=3。

2.3 K值优化选取

采用手肘法和轮廓系数法确定K-means算法中的最优K值。

手肘法评价K值的指标是误差平方和SSE,即

(3)

式(3)中:Ci为第i个簇;Ni为Ci中的样本个数;Pj=(pj1,pj2, …,pjm)属于Ci中的第j个样本,oi=(oi1,oi2, …,oim)为第Ci的质心。

这种方法得到的SSE值与K值关系图像类似一个手肘形,肘部对应的K值被认为是最优K值。

轮廓系数法评价K值的指标是轮廓系数SC,即

(4)

式(4)中:a(i)为第i个样本与簇类其他样本的平均距离,称为凝聚度;b(i)为第i样本与最近簇中所有样本的平均距离,称为分离度。

平均轮廓系数的取值范围为[-1, 1],与最大SC值对应的K值即为最优K值。

2.4 聚类结果

由土力学知识可知,土的含水率、湿密度、比重为土的三个基本参数,其他物理指标往往可由这三个指标进行推导,且这三个基本参数与土的力学性质也有着密切联系[13,18]。所以,本次研究中将选用含水率、湿密度、比重这三个基本参数对土进行二级分类。

本次聚类分析中,将包含缺失值的三个基本参数样本剔除,最终保留638个完备的基本参数样本。首先,根据2.1节的归一化方法对数据样本开展归一化处理,然后利用2.3节的方法比选最优K值,结果如图4所示。由图4可知,SSE随着K值的增大逐渐减小,当K值从2增长为3时,SSE的下降幅度最大;与此同时,SC在K=3时具有最大值。因此,最优K值为3。

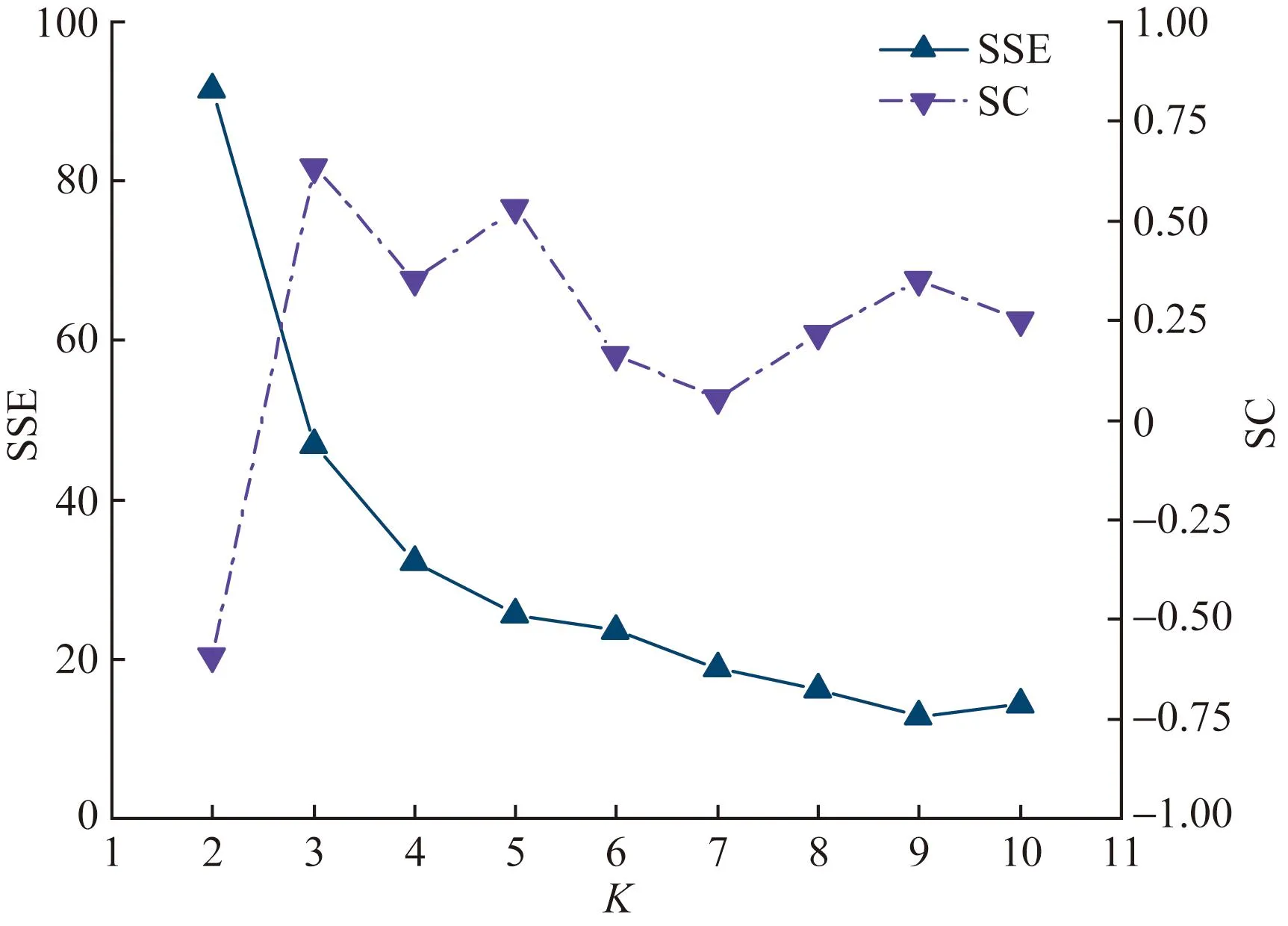
图4 SSE和SC与K的关系图Fig.4 Variations of SSE and SC with K

从图5可以看出,原始数据样本分成了三个簇,代表三个亚类土,分别命名为DCLS-I(滇池湖相土第I亚类,dianchi lacustrine soil-I)、DCLS-II(滇池湖相土第II亚类,dianchi lacustrine soil-II)和DCLS-III(滇池湖相土第III亚类,dianchi lacustrine soil-III)。不难发现,DCLS-I的数据样本代表了含水率较低、土粒比重大、湿密度也大的一类土;DCLS-III代表了含水率高、土粒比重较小、湿密度也较小的一类土;DCLS-II代表介于DCLS-I和DCLS-III的一类土。此外,DCLS-I和DCLS-II的分割界限明显,且三类土的样本数据几乎没有交叉,说明本次聚类分析比较成功。DCLS-I、DCLS-II和DCLS-III在归一化空间中的聚类中心分别为(-0.872, 0.737, 0.634)、(-0.478, 0.240, -0.161)和(0.157, -0.482, -0.663),如图5(a)所示;在原始数据空间中分别为(27.96, 2.674, 1.906)、(67.693, 2.455, 1.484)和(131.905, 2.138, 1.219),如图5(b)所示。

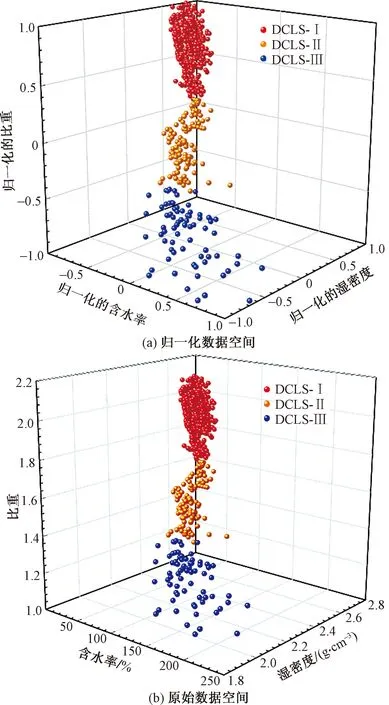
图5 聚类分析结果Fig.5 Clustering results

3 土性参数数理统计特性表征

3.1 基本统计特征分析

首先分析三个亚类土的基本统计特征,如表1所示。对于每个参数的整体基本统计特征,读者也可以根据表1中第2、3、4列展示的样本量,按照比例关系进行加权平均计算获得。

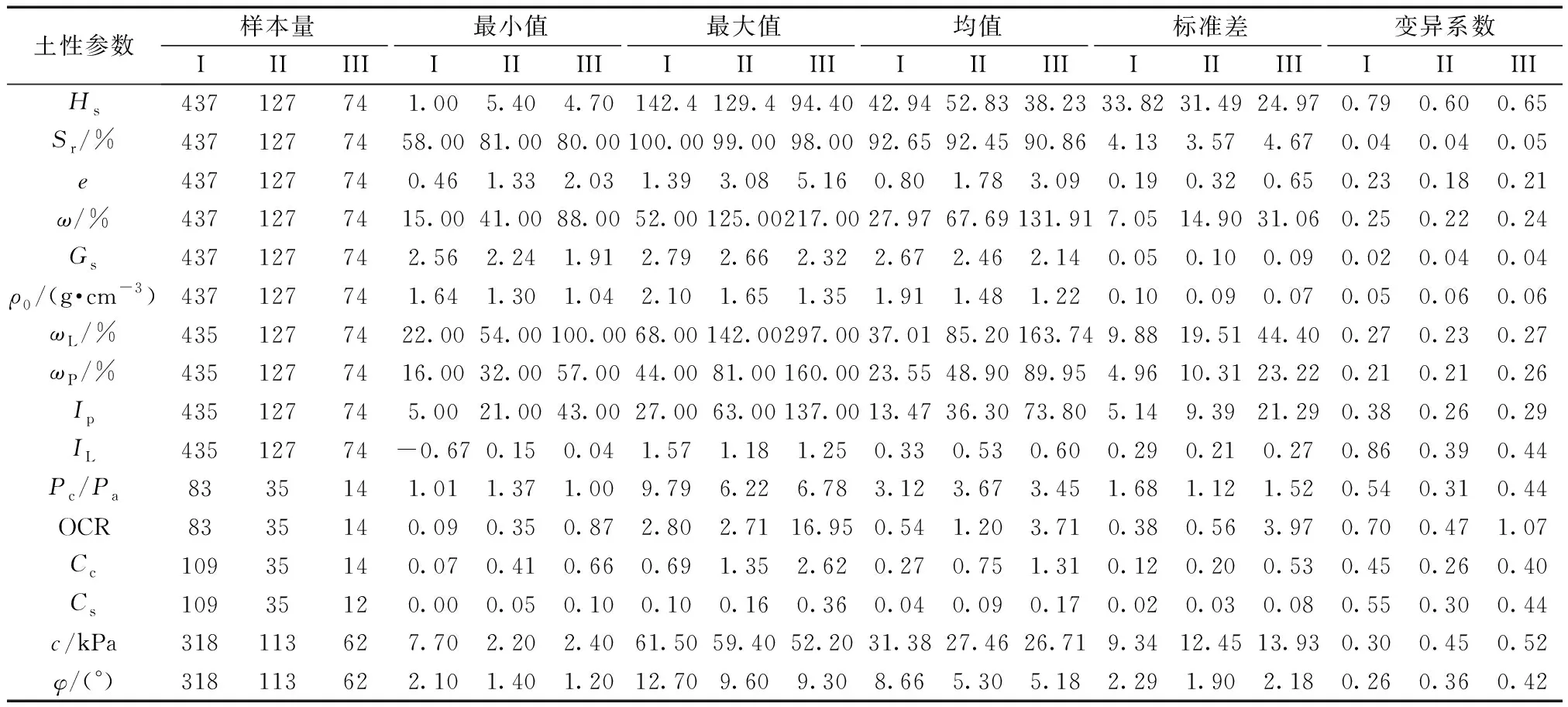
表1 DCLS-I、DCLS-II和 DCLS-III类土土性参数的基本统计特征Table 1 Basic statistical characterization of soil parameters for DCLS-I, DCLS-II, and DCLS-III

从采样深度来看,三类土的钻孔深度分别达到142.4、129.4、94.4 m,符合了绝大多数地下工程施工对于钻探深度的要求。从Sr来看,由于三类土是湖相土,样本的平均Sr均达到了90%以上;从e来看,三类土的平均e分别为0.8、1.78和3.09,说明DCLS-I最密实、DCLS-II次之、DCLS-III最疏松;从ω来看,三类土的平均ω分别为27.97%、67.69%和131.91%,反映出DCLS-I类土工程性质受水的影响最小,DCLS-II类土次之,DCLS-III类土最大;从Gs来看,三类土的平均Gs依次减小,分别为2.67、2.46和2.14,ρ0也表现出类似的特征;三类土的平均ωL和ωP依次增大,分别为37.01、85.20、163.74和23.55、48.90、89.95;同时,三类土的IP也依次增大,分别为13.47、36.30和73.80,表明三类土的黏土矿物含量也依次增大;三类土的IL也呈现依次增大的现象,依次为0.33、0.53和0.60,表明三类土的硬度逐渐下降;三类土的Pc/Pa从整体来看没有明显趋势,分别为3.12、3.67和3.45;而三类土的超固结比OCR呈现出了依次增大的现象,依次为0.54、1.20和3.71,DCLS-I类土整体上为欠固结状态,DCLS-III类土整体为超固结状态,DCLS-II类土近似处于正常固结状态;三类土的Cc也呈现依次增大的现象,依次为0.27、0.75和1.31,表明这三类土的可压缩性越来越大;此外,三类土的Cs也呈现依次增大的现象,依次为0.04、0.09和0.17,表明三类土导致基坑隆起的可能将依次增大;三类土的c依次下降,分别为31.38、27.46、26.71 kPa;三类土的φ也依次减小,分别为8.66°、5.30°和5.18°。

对于岩土材料,一般密度和比重越大,含水率越小,其工程性质越好。从表1可知,本次聚类分析的成果比较符合上述规律。

3.2 深度趋势分析

由于应力历史的作用,许多土性参数在深度方向上会表现出某种趋势,不确定性量化分析中如果不将这种趋势去除,将会高估参数的不确定性[12]。

图6、图7和图8分别展示了三个亚类土的土性参数深度趋势,可以看出,不同参数的深度趋势差异显著。比如,DCLS-I类土仅OCR、c和φ表现出了微弱的趋势,其余参数没有明显趋势; DCLS-II、DCLS-III类土IL、Pc/Pa、OCR、Cc、Cs、c和φ均有较明显的趋势,其余参数趋势不明显。

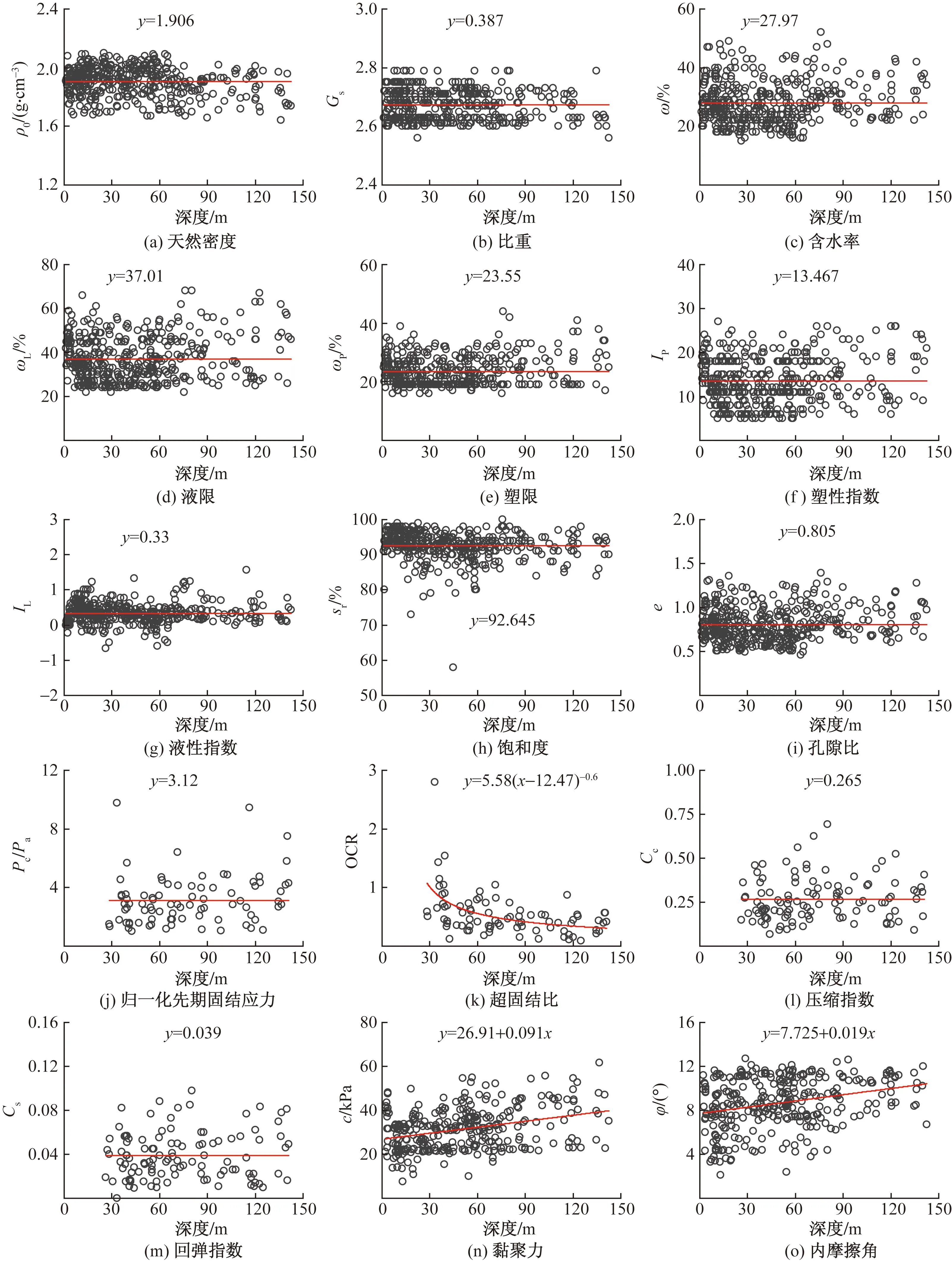
图6 DCLS-I类土的土性参数深度方向趋势表征Fig.6 Trend of soil parameters for DCLS-I

图7 DCLS-II类土的土性参数深度方向趋势表征Fig.7 Trend of soil parameters for DCLS-II

图8 DCLS-III类土的土性参数深度方向趋势表征Fig.8 Trend of soil parameters for DCLS-III

对于DCLS-I类土,图6(k)显示出OCR随深度增加而减小的趋势,且在20～150 m深度范围内OCR的减小趋势比较符合幂函数形式。图6(n)和图6(o)分别反映出c和φ随深度呈现轻微增加的趋势,但数据样本的离散型很大,表明DCLS-I类土的强度性质受深度影响不大。由图6(a)～图6(j)、图6(l)和图6(m)可知,ρ0、Gs、ω、ωL、ωP、Ip、IL、Sr、e、Pc/Pa、Cc和Cs均没有明显的深度趋势。

对于DCLS-II类土,图7(n)和图7(o)表明此时c和φ具有随深度增加的趋势,且趋势更符合对数函数。此外,对于DCLS-II类土,IL也表现出随深度减小的趋势,其减小规律符合幂函数如图7(g)所示。图7(j)表明Pc/Pa在DCLS-II类土中也呈现随深度增加的趋势,这种趋势可以近似用线性函数进行描述。图7(l)和图7(m)反映出Cc和Cs均随深度有以幂函数形式减小的趋势,说明随着深度增加,DCLS-II类土引起的压缩性和回弹性将逐渐减弱。ρ0、Gs、ω、ωL、ωP、Ip、e等参数均未表现出深度方向上的趋势,如图7(a)～图7(f)和图7(h)所示。

对于DCLS-III类土,IL、Pc/Pa、OCR、Cc、Cs的深度发展趋势与DCLS-II类土相似,如图8(g)和图8(i)～图8(m)所示,尽管c和φ表现出随深度增加的趋势,但此时的趋势更加符合线性函数如图8(n)和图8(o)所示。从图7(a)～图7(f)和图8(h)可知,ρ0、Gs、ω、ωL、ωP、Ip、Sr、e等参数仍未表现出明显趋势。

综合观察上述三类土,可以发现Sr均大于80%,说明本场地的土总体处于饱和状态[18],在岩土工程结构设计时,需采取抗振动液化的措施。另外,三类土的ρ0、Gs、ω、ωL、ωp、IP、e均随深度均没有明显趋势。图6～图8所表现出来的土性参数趋势规律,应当从湖相土的沉积过程、土体微观结构以及水的渗透规律等多方面深入分析,但这超出了本文的研究范围,期望在后续研究中可被进一步探索。

3.3 参数统计分布特性检验

根据相关研究,岩土工程参数的统计分布特性明显[19]。所以,在3.2节的基础上进一步研究各类土的各参数的统计分布模型。为此,选取了常用的5种分布模型,分别是正态分布、对数正态分布、韦伯分布、伽马分布和极值分布,这5种分布模型的标准型概率密度函数分别为

(5)

(6)

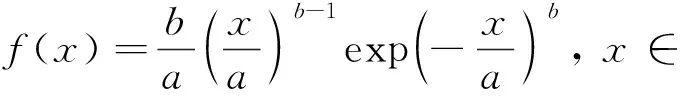
(7)

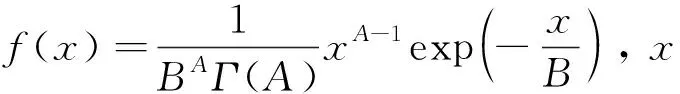
(8)

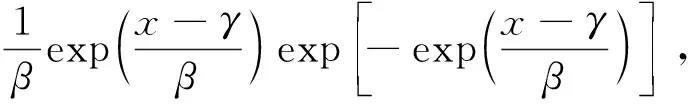
(9)

式中:x为土性参数数据;μ和σ分别为土性参数数据的均值和标准差;λ和ξ分别为土性参数数据取对数后的均值和标准差;a和b分别为韦伯分布的位置和形状参数;A和B分别为伽马分布的位置和形状参数;γ和β分别为极值分布的位置和形状参数;Γ(·)为伽马函数。

为评估理论分布模型对实际数据分布的拟合效果,利用MATLAB的内置函数开展K-S(Kolmo-gorov-Smirnov)检验,如果输出的P值大于给定的显著性水平α,则通过检验。参考相关研究[13],本文α取0.05。由于对数正态分布、韦伯分布和伽马分布要求变量大于0,所以,对于没有明显趋势且始终为正值的参数,直接开展统计分布模型的检验;而对于有趋势的参数,先移除趋势,再对残余值开展正态分布和极值分布的K-S检验。K-S检验结果如表2所示。

表2 DCLS-I～DCLS-III类土的部分土性参数统计分布模型比选Table 2 Selection of distribution models for partial soil parameter of three types of soils

对于DCLS-I类土,在α为0.05时,ωL、ωP、IL、IP和e没有通过上述5个模型中的任何一个模型的检验,若将α放宽至0.01,ωL和e将可认为服从伽马分布。最佳分布模型方面,Pc/Pa、Cc对应对数正态分布,Cs对应韦伯分布,OCR、c和φ残余值对应正态分布。

图9展示了ωL、ωP、IL、IP、e和c的实际分布与理论分布的对比,其中仅有c的检验得到了通过。对比图9(a)～图9(e)与图9(f),可以发现,尽管ωL、ωP、IL、IP和e的分布模型检验未通过,但直观上还是处于可接受范围,因此在必要时,可利用与实际分布较吻合的理论模型进行数据模拟[13]。

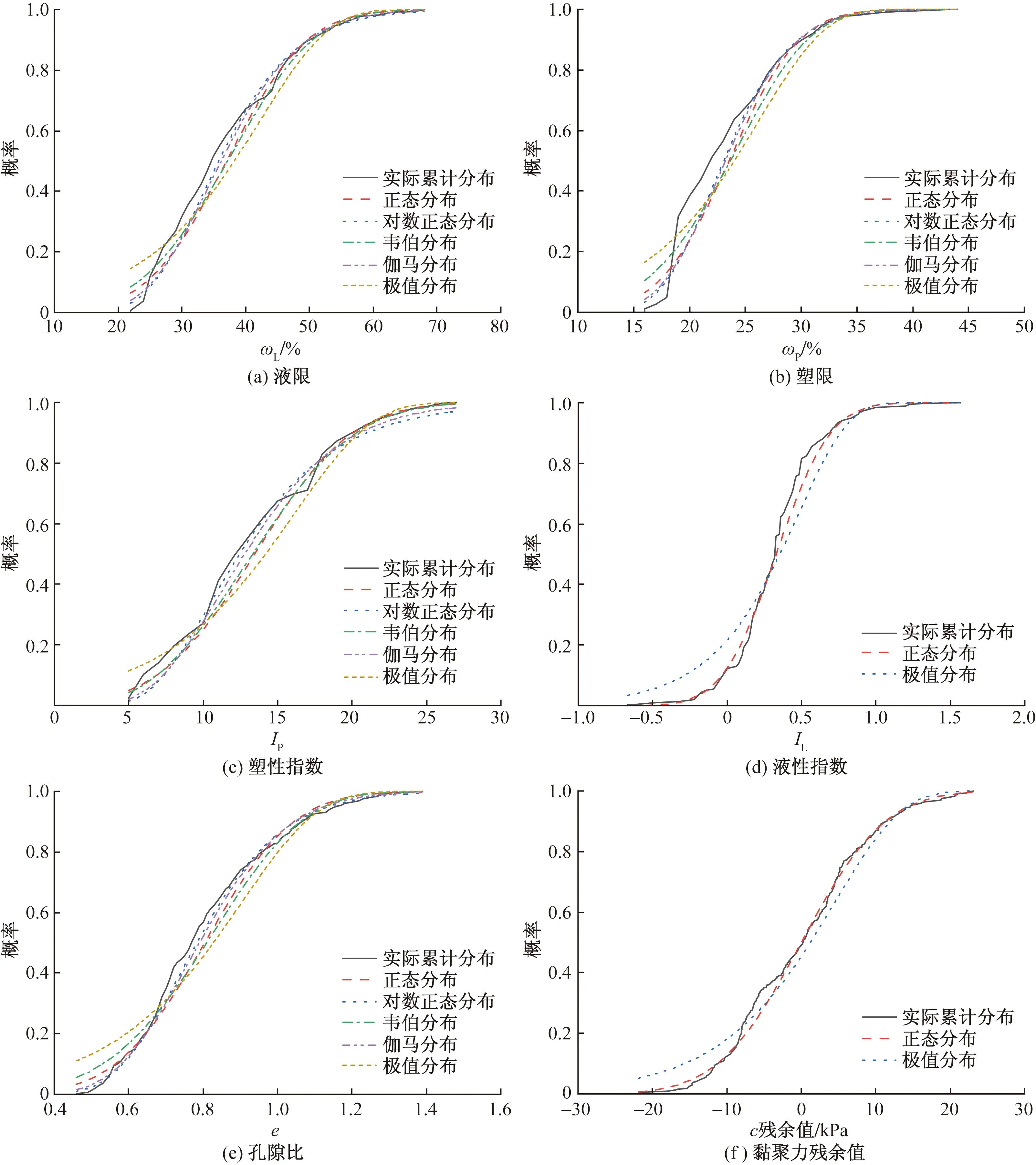
图9 DCLS-I类土部分参数数据或残余值的分布模型检验Fig.9 Testing of distribution models for partial soil parameters or their residuals of DCLS-I

对于DCLS-II类土,所有参数数据或去趋势后的残余值都满足上述一种或几种分布模型,ωL、IP、e等参数的最佳分布模型对应对数正态分布,ωP对应伽马分布,IL、Pc/Pa、OCR、Cc、Cs、c和φ等残余值对应正态分布。对于ωP,对数正态分布的p值仅稍小于伽马分布,因此也可以很好地用对数正态分布对ωP数值进行模拟。对于DCLS-III类土,ωL、ωP和e等参数的最佳分布模型对应对数正态分布,IL残余值的对应极值分布,Pc/Pa、OCR、Cc、Cs、c和φ残余值对应正态分布。

ρ0、Gs和ω为本次聚类分析中的三个基本参数,不适宜单独根据亚类进行统计分布特性检验,而是应当进行整体分析。从表3可知,上述5种模型均不能较好地模拟这三个基本参数的统计分布特征。图10展示了5种理论模型与实际分布的差异,可以看出Gs实际分布曲线的平滑度非常低,这是因为重复数据过多,ρ0和ω的曲线平滑性较好。此外,从图10中还可看出,尽管模型与实际分布的吻合度不高,但总体分布趋势一致,所以,也可以选出比较符合的模型近似模拟参数数据的统计分布,比如Gs和ρ0可以用韦伯分布或者极值分布进行近似,而ω可以采用对数正态分布进行近似。

表3 三个基本参数的统计分布模型比选Table 3 Comparison of distribution models for three basic parameters

图10 三个基本参数的分布模型检验Fig.10 Testing of distribution models for three basic parameters

3.4 相关性分析

岩土参数之间通常具有多元相关性,而且严格来讲,多元相关性的分析需要一套完备的多元数据[12-13]。实际工程中,一个土样往往只能开展有限个试验,由此造成数据不完备。尽管如此,可借助Bootstrapping算法,通过参数之间的两两相关性构建多元相关系数矩阵[13]。通过Bootstrapping算法对每一对参数获取了1 000个相关系数样本,然后提取了1 000个正定矩阵,最终由此计算出相关系数的90%置信区间(由5%和95%分位数定义)和均值,而且正定矩阵的均值也是正定矩阵[13]。考虑到参数之间可能存在非线性相关,本文研究中的相关系数是斯皮尔曼相关系数,而非皮尔逊相关系数。

首先分析三个基本参数的相关矩阵,此时没有区分亚类,结果如表4所示。可以看出,均值全部落在置信区间内,含水率和湿密度具有最强的相关性(-0.98),其次是比重和湿密度,含水率和比重的相关性最低。

表4 三个基本参数的相关系数矩阵Table 4 Correlation matrix of three basic parameters

分析各亚类的土性参数相关性时,没有将所有参数纳入分析。一是由于矩阵太大,结果不容易收敛;二是因为部分参数之间可以相互推导,则不需要纳入。所以,选取了IL、Cc、Cs、c和φ5个参数开展多元相关性分析。

表5列出了DCLS-I类土的相关系数矩阵,可以看出,Cs和Cc具有最强的相关性,其次是Cs和φ等,最弱的是IL和Cc。值得注意的是,DCLS-I类土的c和φ呈正相关,但平均相关系数仅为0.16。另外,Cc与c呈现正相关,而与φ呈负相关,说明对于DCLS-I类土,进一步降低土体的压缩性会引起黏聚力的下降和内摩擦角的上升。

表5 DCLS-I类土土性参数相关矩阵Table 5 Correlation matrix of soil parameters for DCLS-I

表6列出了DCLS-II类土的相关系数矩阵,可以看出,IL和φ具有最强的相关性(-0.92),其次是IL和c,最弱的是Cc与c。

表6 DCLS-II类土土性参数相关矩阵Table 6 Correlation matrix of soil parameters for DCLS-II

表7列出了DCLS-III类土的相关系数矩阵,可以看出,IL和φ依然具有最强的相关性(-0.93),其次是c和φ,再次是IL和c,最弱的是Cc与Cs。

表7 DCLS-III类土土性参数相关矩阵Table 7 Correlation matrix of soil parameters for DCLS-III

对比表4可以发现,DCLS-II和DCLS-III类土的参数相关特性比较类似,主要表现在这两类的c和φ的平均相关系数均在0.9左右,远大于DCLS-I的0.16。另外,DCLS-II和DCLS-III类土的Cc与c和φ均具有十分微弱的负相关性。对于DCLS-II和DCLS-III类土,与Cc与Cs成对的参数相关系数不确定性一般较大,大多置信区间的宽度大于0.5,这主要是由于这两类土的Cc与Cs数据样本较少。

4 结论

以昆明滇池湖相土为依据,着重研究了湖相粉土的工程性质。主要得出如下结论。

(1)根据土的三个基本参数,借助K-means算法将土样分成了三个亚类,即DCLS-I、DCLS-II和DCLS-III。这三个亚类在归一化数据空间中的聚类中心分别为(-0.872, 0.737, 0.634)、(-0.478,0.240,-0.161)和(0.157,-0.482, -0.663),在原始数据空间的聚类中心分别为(27.960, 2.674, 1.906)、(67.693, 2.455, 1.484)和(131.905, 2.138, 1.219)。

(2)参数深度趋势方面, DCLS-I类土的趋势不如DCLS-II和DCLS-III明显,这是由于DCLS-I类土的密实程度高,受应力历史影响不如后两类土。

(3)统计分布特征方面,在α为0.05时,DCLS-I类土ωL、ωP、IL、IP、e未能通过K-S检验,必要时,可以选取某一较好模型近似模拟;DCLS-II类土的参数数据一般可以通过K-S检验。对于三个基本参数,本文研究从数据整体进行检验,结果显示没有一个理论模型通过K-S检验。类似地,必要时可以选取某一较好模型近似模拟。

(4)利用Bootstrapping算法和斯皮尔曼相关系数对参数数据的多元相关矩阵进行解析,通过多次抽样模拟,获得了三个基本参数以及三类土的IL、Cc、Cs、c、φ的正定多元相关系数矩阵。