标准砂-钢板接触面剪切失效机理的宏细观研究

2024-01-12杨昊杜强

科学技术与工程 2023年34期

杨昊, 杜强,2,3*

(1.内蒙古工业大学土木工程学院, 呼和浩特 010051; 2.沙旱区地质灾害与岩土工程防御自治区高等学校重点实验室, 呼和浩特 010051; 3.内蒙古工业大学地质技术与岩土工程内蒙古自治区工程研究中心, 呼和浩特 010051)

土体与结构物之间的相互作用问题一直是土木工程和岩土工程界研究的重要课题。土与结构物接触面力学特性研究涉及土力学的各方面,如挡墙与墙后土的接触、桩与桩周土的接触、锚杆或土钉与土的接触等。实际工程中常见的钢板桩、钢管桩施工及应用同属于土与结构物接触面的范畴。在受到外部荷载作用时,正确地分析接触面土体的受力变形情况,研究土与结构物相互作用的失效机理,对工程的安全与可靠是必需的,也是至关重要的。

此前,中外诸多学者进行了大量该方面的研究。Potyondy[1]利用应力控制式和应变控制式直剪仪研究了多种土料与结构物材料接触面的力学特性,提出影响界面摩擦强度的4个主要因素:土质、含水率、界面粗糙度和正应力;Desai等[2]认为两种材料接触面剪应力传递和剪切带的形成发生在接触面附近的一薄层土体中,进而提出薄层单元的概念;Clough等[3]利用直剪试验研究土与混凝土接触面的力学特性,提出接触面剪应力与相对剪切位移为双曲线关系;殷宗泽等[4]通过直剪试验实验研究分析提出了刚--塑性变形的观点并在此基础上提出了一种可以与土体的非线性弹性模型或弹塑性模型相衔接的有厚度的接触面单元;胡黎明等[5-6]利用改进的直剪仪对不同接触面相对粗糙度的砂土与结构物进行剪切试验,分析了土与结构物接触面剪切破坏的变形机理;张嘎等[7-9]运用数字图像技术对多种粗粒土与人工粗糙钢板接触面的力学特性进行研究,建立了跟踪土粒运动的位移测量方法。

在此基础上,刘文白等[10]通过试验分析和数值模拟研究土与结构物相互作用接触面最大剪应力的变化规律;冯大阔等[11-12]通过进行不同应力幅值比下粗粒土与结构接触面大型三维循环直剪试验,分析了接触面切向位移、剪切柔度及应力幅值比的影响;郑铮等[13]利用自行研发的深海沉积物-结构界面仪对静/动载作用下不排水深海沉积物-结构界面特性试验并进行研究,研究结果表明静载作用下界面应力曲线随着粗糙度的增加由折线型转变为双曲线型;Kou等[14]对不同粒径的钙质砂和不同表面粗糙度的钢板进行直剪试验,发现纯砂直接剪切试验得到的峰值剪应力高于界面剪切试验得到的值;朱俊高等[15]利用改进的直剪仪对不同密实度的粗粒土与钢板接触面进行直剪试验,探究发现粗粒土与钢板之间的接触面在达到剪切破坏前,剪应力与剪切位移之间近似呈线性关系。接触面的抗剪强度及切向劲度系数均随着粗粒土相对密实度的增大而增大,赵程等[16]通过在剪切盒内注色进行研究从宏观角度发现了粗砂与结构物剪切带厚度和法向应力呈正相关且剪切带空间分布不均匀;Namjoo等[17]采用多种砂对不同材料进行剪切试验以探究接触界面的剪切行为;史乃伟等[18]利用大型直剪设备以及颗粒流软件对粗砂进行直剪试验和数值模拟,结果表明粗砂的临界状态摩擦角为36.4°～37.4°且实验过程中初始正应力、初始相对密实度对临界状态摩擦角影响可忽略;卢孝志等[19]对不同砂泥岩配合比在不同法向应力分条件下进行剪切试验,通过引入泥岩含量m,发现随泥岩含量增加,黏结力线性增大而内摩擦角呈二次方减小;赵春风等[20]通过对不同种粗糙度的砂土-混凝土接触面在不同固结法向应力下进行的加、卸荷直剪试验,分析不同加、卸荷状态下接触面的力学特性,得出固结法向应力主要通过影响接触面土体密实度和含水率间接对峰值剪切应力产生影响;杨烜宇等[21]对不同形态接触面和不同材质的试样进行直剪试验,分析发现宏观表现为抗剪强度的差异,即颗粒重新分布及接触面闭合共同作用导致试样的法向变形。

以上研究表明,目前关于土与结构物相互作用的分析与研究中,在宏观方面已取得了一定的成就,形成了比较成熟的宏观试验体系和相应的研究方法。但在土-结构物细观层面和土-钢接触面的试验与理论研究还比较少,尤其是应用离散元研究土与结构接触面力学特性的工作开展得还非常有限,缺少土与结构物相互作用的宏细观相结合的分析方法。同时,对于土与结构物相互作用失效机理的研究也比较少。为此,现基于改进后的半模直剪仪进行标准砂-钢板单调剪切试验,从宏观、细观两方面对标准砂-钢板接触面剪切失效机理进行分析和研究。

1 试验方案

1.1 试验材料

试验选取厦门艾思欧标准砂有限公司生产的国际标准化组织(International Organization for Standardization, ISO)标准中砂,粒径范围为0.5～1.0 mm,其物理力学特性如表1所示,颗粒级配曲线如图1所示。

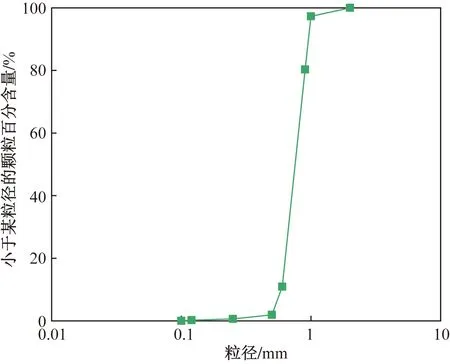
图1 标准砂颗粒级配曲线Fig.1 Standard sand particle gradation curve

表1 砂样物理力学性质指标Table 1 Physical and mechanical properties of sand samples

表2 加载方案Table 2 Loading scheme

1.2 试验装置

采用特制的半模直剪仪对标准砂-钢板进行单调剪切试验,试验仪器如图2所示。

图2 试验仪器Fig.2 Test equipment

参考本课题组现有可视化仪器[22],对实验装置进行改进,该试验装置较于传统直剪仪增加了特有的观察窗口,可在试验过程中观察到砂-钢板剪切过程中接触面的变形特征。对照本课题组已有的土颗粒细观观测手段[23],试验中所用图像采集装置为USB数码显微镜(BELONA牌0X-200X-800X型),图像分辨率可达1 600×1 200,数码变焦,最大放大倍数为800X,如图3所示。

图3 数码显微镜Fig.3 Digital microscope

1.3 试验过程

将半圆钢板置于直剪仪下盒内,利用半模直剪仪进行不同初始相对密实度下的标准砂-钢板单调剪切试验。通过最大、最小孔隙比计算出试验要求密实度所需的砂样密度,根据剪切盒体积计算出对应的质量,量取所需的砂样后,用砂雨法分层制样,可以较好地控制其相对密度。试验采用等速剪应变,剪切速率为0.4 mm/min。加载方案如表 2 所示。

2 单调剪切试验结果及宏细观分析

2.1 标准砂-钢板单调剪切试验

图4给出了不同初始密实度、不同法向应力下标准砂-钢板单调剪切的剪应力-位移关系曲线。

图4 标准砂与钢板剪应力-位移关系曲线Fig.4 Standard sand and steel plate shear stress-displacement curve

由图4可知,不同初始密实度的标准砂与钢板进行单调剪切试验时,土体的剪应力均随着钢板位移的增加而增大,达到最大剪应力后趋于稳定。在同一密实度下,随着法向应力的增加,土体的剪应力也在增加。可以将剪应力-位移关系曲线分为三个阶段,即剪应力线性增长阶段、缓慢增长阶段和水平发展阶段。

初始相对密实度对标准砂-钢板单调剪切接触面强度有影响。Dr=90%时,在法向应力σ=100、200、300、400 kPa的条件下与钢板作用的峰值强度分别是Dr=60%时的1.5倍、1.2倍、1.11倍、1.31倍。产生的原因是当砂样密实时,砂土颗粒排列紧密,颗粒间的咬合力较大。在砂与钢板接触作用的区域里,土颗粒发生转动和重新排列的概率较小,在相同位移条件下,剪切过程中要克服颗粒间较大的咬合摩擦,在接触面产生较大的抗剪切强度。当密实度较小时,土颗粒间孔隙大,颗粒在剪切过程中发生重新排列,在相同剪切位移条件下,剪切过程中克服较小的咬合摩擦,接触面抗剪切强度低。

2.2 基于应力-位移关系分析标准砂-钢板相互作用

选取法向应力σ=300 kPa条件下不同初始密实度的标准砂与钢板的单调剪切试验结果进行分析。其剪应力-位移关系曲线如图5所示。

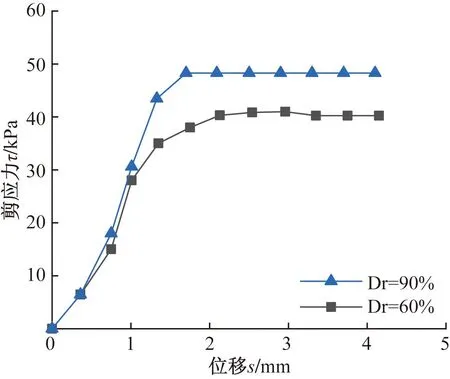
图5 σ=300 kPa不同初始密实度标准砂-钢板剪应力-位移曲线Fig.5 σ=300 kPa different initial density standard sand-steel plate shear stress-displacement curve

标准砂-钢板进行单调剪切试验时,随着相对位移的增加,接触面的剪应力逐渐增大并趋于稳定,剪应力-位移关系曲线呈现出应变硬化的状态。曲线并无明显的剪应力峰值,可视为理想弹塑性模式。令λ为相邻两位移点所对应剪应力差值,将计算出的λi列入表3中。

表3 λi计算结果统计表Table 3 Statistics of λi calculation results

由表3可知,初始密实度Dr=90%的砂样自λ6开始,λi不再变化,一直为0,说明从第6个位移点(s=1.7 mm)开始,剪应力的大小不再随着位移的增加而改变,可认为此位移所对应的剪应力值为砂样与钢板单调剪切时的抗剪强度;初始密实度Dr=60%的砂样自λ10开始不变。对照两种条件下的λi值的变化可知,相同条件下密实度较大的砂样在单调剪切时抗剪强度更高,密实度较低的砂样会经历更长的位移。

图4(b)中σ=400 kPa时Dr=90%标准砂与钢板相互作用剪应力-位移关系曲线。在位移至约为2 mm时剪应力不再变化。由此可知,当砂样与钢板间的相对位移增加,而对应的剪应力增量λi趋于0时,认为砂样与钢板之间已发生失效。对应到剪应力-位移关系曲线,认为当曲线进入水平发展阶段时,砂样与钢板相互作用失效。

2.3 基于孔隙变化的细观分析

选取标准砂-钢板接触面区域进行细观分析,观测点位置如图6所示。

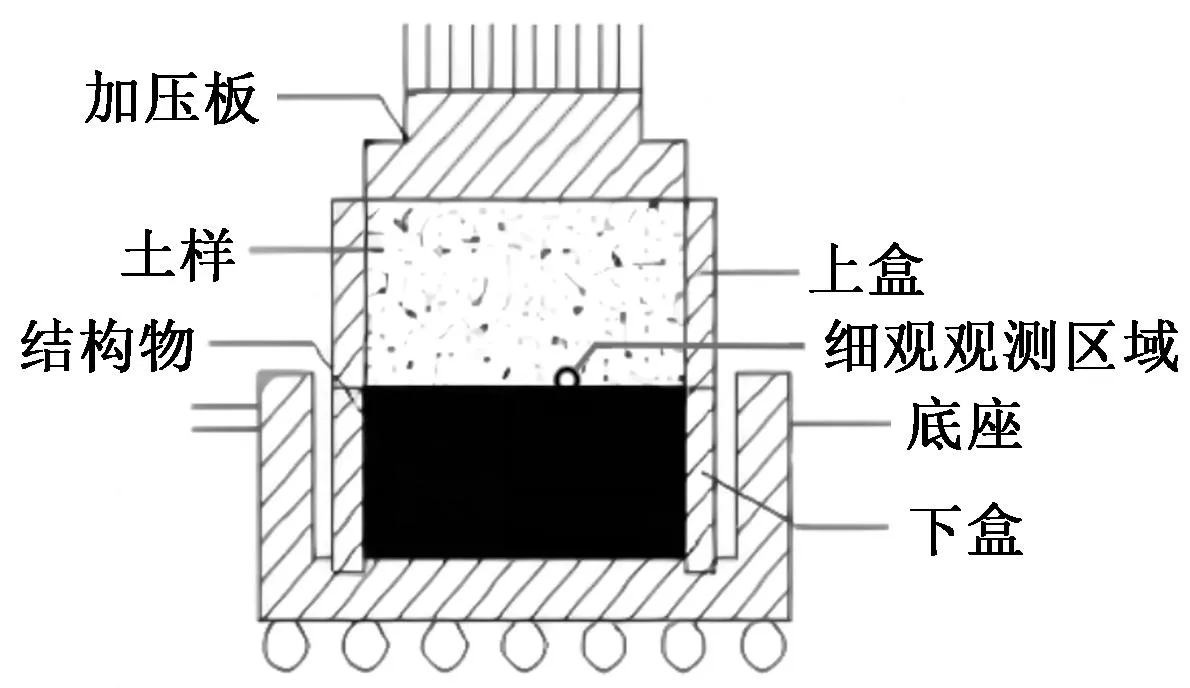
图6 观测点位置示意图Fig.6 Position diagram of observation point

在观测点拍摄细观图片,对法向应力σ=300 kPa,密实度 Dr=90%标准砂-钢板单调剪切试验所拍摄的细观观测照片进行分析。图7(a)为数码显微镜拍摄的细观原始图片,照片的尺寸为1 280×1 024,放大倍数为50倍,镜头内颗粒数目约为50颗,分析测点均指单元中心点。用 MiVnt自带的图片处理工具将砂土颗粒圈出并涂黑渲染,涂色颗粒以外的区域为孔隙,处理效果如图7(b)所示。

二维细观分析时将土的孔隙率定义为观测面中孔隙的总面积与土颗粒的总面积之比,即单位面积内的孔隙面积,利用MiVnt图像分析系统对图像的孔隙面积和分析区域总面积分别做出统计。在标准砂-钢板单调剪切试验过程中进行不同位移等级条件下细观照片的拍摄,选取相对位移为0、1、2、3、4 mm时进行拍摄,用MiVnt软件处理得出颗粒及孔隙的结果如表4所示。

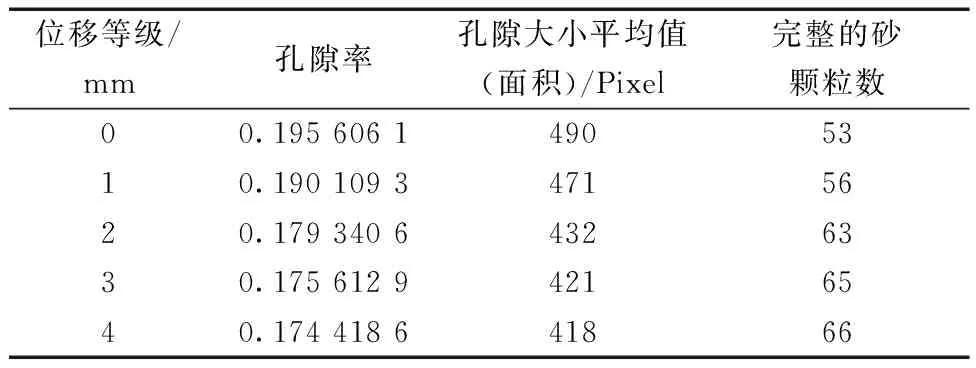
表4 不同位移等级下的颗粒与孔隙参数Table 4 Particle and pore parameters under different displacement levels

比较表4中所列细观参数可以得出,标准砂-钢板剪切过程中,随着位移等级的增大,砂土的孔隙率逐渐减小,其原因是法向应力和剪切应力的作用,土体不断压缩,颗粒发生挤压和旋转并不断填充孔隙。可知最后一个阶段在4个不同试验阶段中孔隙率变化最小。位移等级s=1 mm 至位移等级s=2 mm 的阶段,孔隙率变化最大。对比不同位移等级下孔隙大小的平均值,可以看出随着位移等级的递增,孔隙大小的平均值呈现出减少的趋势。在位移等级s=2 mm后,孔隙大小的平均值减小的幅度降低。

上述分析表明标准砂-钢板单调剪切过程中砂样孔隙的压缩主要发生在开始阶段,随着试验的进行砂样密实度提高、孔隙压缩程度减小、孔隙面积减小。通过上述分析判定颗粒的孔隙率和孔隙发生显著的变化时标准砂-钢板单调剪切失效。显微图像拍摄的范围是固定的,由出现在图像内的完整的砂土颗粒逐渐增加可看出土体不断压缩,单位面积内的砂土颗粒逐渐增加,孔隙率及孔隙大小的变化情况基本一致。

2.4 基于颗粒间接触关系的细观分析

除颗粒孔隙及形状大小能反映砂土细观结构以外,粒间接触关系也是一个重要细观参数,对此使用颗粒的接触线切线方向来表示。在MiVnt软件中以接触曲线段两端点相连所得的直线,即以割线的方向近似作为切线方向来表示颗粒间的接触关系。图8为相应位移等级下细观观测点内颗粒接触线切线方向玫瑰图。

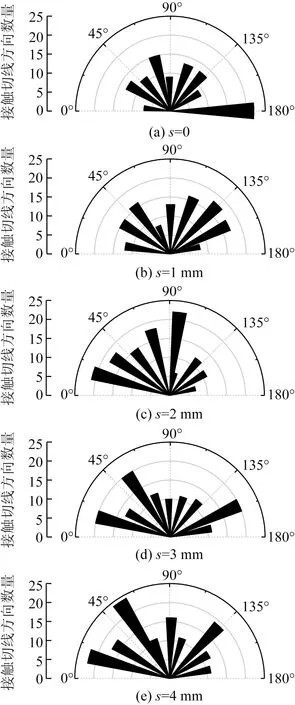
图8 接触线切线方向玫瑰图Fig.8 Rose diagram of tangent direction of contact wire

由图8可知,颗粒接触线总数随位移等级增加而增加。接触线切线方向与x轴正向的夹角分布随位移等级的增加逐渐由90°～180°向 0°～90°转变。自然堆积状态下接触线方向的分布具有一定的随机性,接触线切线方向与x轴正向夹角为160°～180°区间内的接触线最多,有22个,占接触线总数的19.82%;而接触线切线方向与x轴正向夹角是0～20°的区间内的接触线有7个,占总数的6.31%。随着位移等级的增加,当位移等级为s=2 mm时,16.15% 的接触线分布在接触线切线方向与x轴正向夹角0～20°的区间内,而接触线分布在接触线切线方向与x轴正向夹角是160°～180°的区间内的概率下降为 5.38%。当位移等级达到s=4 mm时,接触线分布在接触线切线方向与x轴正向夹角是 0～20°区间内的数目是 22 个,占接触线总数的15.38%,分布在接触线切线方向与x轴正向夹角160°～180°范围的接触线11个,占总数的7.69%。

颗粒接触线分布概率的变化以及颗粒排列的定向特征表明在标准砂与钢板单调剪切过程中,标准砂颗粒排列方向随着钢板位移的增加而发生了变化,砂土颗粒在三维空间内发生了重新排列。颗粒之间的接触随着结构物位移的增加而增加。

3 数值模拟及分析

利用颗粒流离散元程序PFC2D,以4道刚性墙体分别来模拟结构物和试样盒,通过对顶面墙体施加不同的速度,并使底面的墙体以一定的速率水平移动,来模拟不同法向应力条件下,土与结构物的相互作用。以具有一定刚度和粗糙度的圆盘来模拟土颗粒。对不同法向应力条件下土与结构物相互作用时土颗粒的分布变化情况、速度场和位移场进行分析。土与结构物相互作用数值模拟模型示意图如图9所示,数值模拟细观参数如表5所示。

图9 土与结构物相互作用数值模拟模型示意图Fig.9 Numerical simulation model of soil-structure interaction

表5 PFC2D模型基本参数表Table 5 Basic parameters of PFC2D model

对密实度Dr=90% 法向应力σ=300 kPa条件下的标准砂-钢板单调剪切试验进行数值模拟,利用颗粒流离散元软件编写相应的程序命令控制结构物 0.4 mm/min 的速率水平运动,使土与结构物产生相对的剪切作用。

3.1 颗粒接触力分析

绘制颗粒接触力分布图和颗粒位移矢量图。选取剪切位移为0、1、2、3 mm的数据点进行分析,颗粒接触力分布如图10所示。

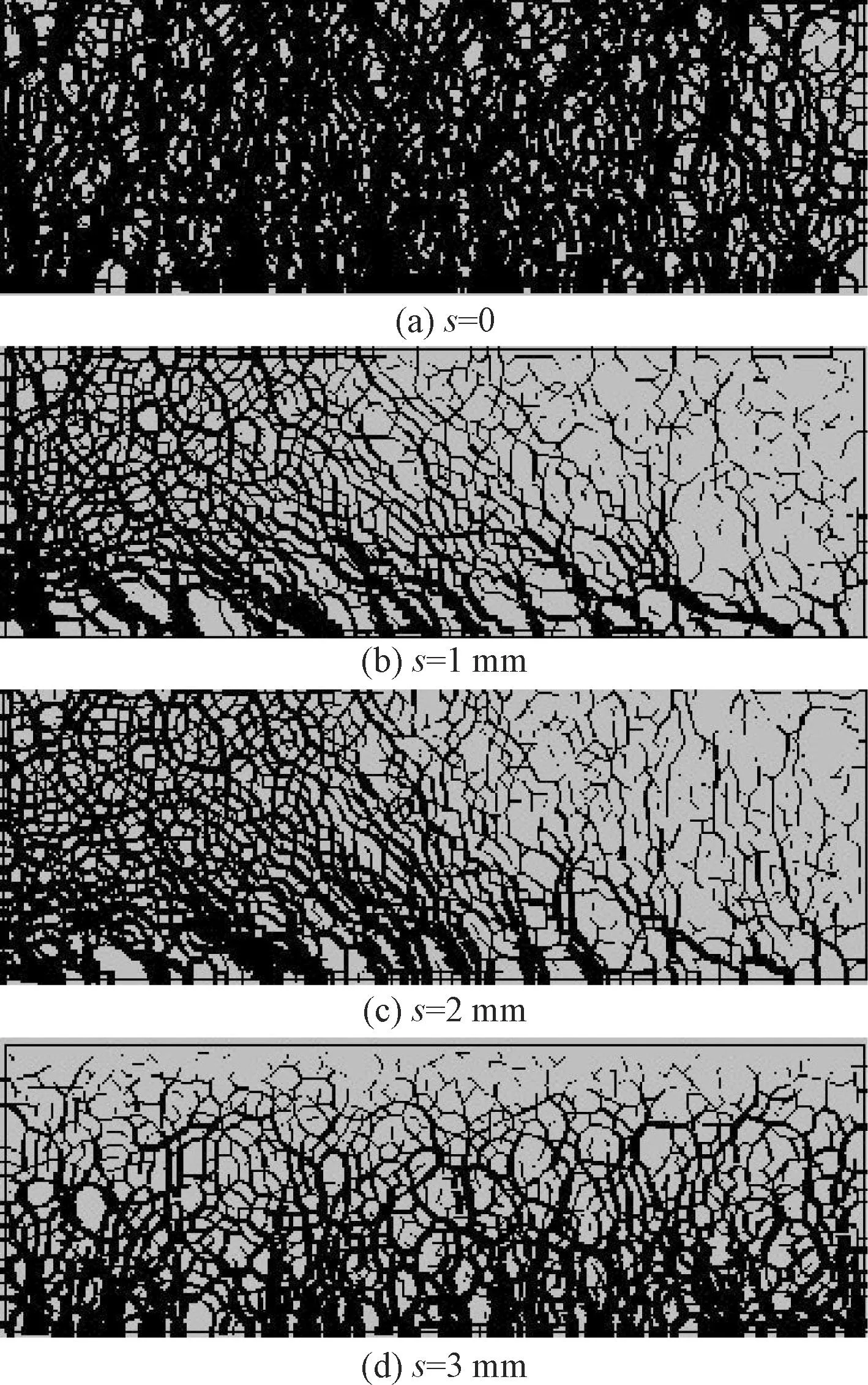
图10 不同位移条件下的颗粒接触力分布图Fig.10 Distribution of particle contact force under different displacement conditions

对比图10,在初始状态(s=0 mm)时粒间接触力分布均匀且主要以竖向为主,此时接触力由自重引起。随着相对位移的产生,在s=1 mm 时,接触力方向逐渐发生偏转,方向与钢板运动方向一致,分布呈斜对角分布,可看出砂样右侧接触力减小,左侧接触力增加。这是由于钢板的运动带动颗粒运动引起的。随着相对位移的增加,颗粒接触力逐渐集中于接触面处并且逐渐增加。在s=3 mm时,接触力又重新恢复以竖向为主,表明砂样与钢板相互作用失效时颗粒受到的粒间作用力已经大于结构物的作用力,此时颗粒基本不随结构物的运动而运动,可判定土与结构物之间已发生失效。

3.2 颗粒位移矢量分析

图11为不同位移条件下的颗粒位移矢量图。对比可知,在初始状态s=0时,颗粒的位移较为杂乱,其原因为填充刚结束颗粒较不稳定。随着相对位移的产生,s=1 mm时,靠近钢板的颗粒在钢板的带动下开始发生水平位移,此时位移具有明显的方向性,其方向与钢板运动方向一致。相对位移进一步增加,接触面处的颗粒位移也随之增加,而距离钢板越远,位移越不明显,说明此时只有与钢板接触的颗粒受到钢板运动的影响。当相对位移s=3 mm 时,颗粒的位移明显减少,说明此时颗粒几乎不随着钢板的运动而运动,只有接触面附近的颗粒发生一定的转动。颗粒不再随着钢板的运动而运动时,标准砂-钢板相互作用发生失效。失效后,土与钢板之间处于塑性滑动状态,土体不再发生明显的形变,位移集中在接触面处发生。

图11 不同位移条件下的颗粒位移矢量图Fig.11 Particle displacement vector diagram under different displacement conditions

3.3 颗粒速度矢量分析

图12为颗粒速度矢量分布图。在初始阶段s=0时,颗粒没有速度,保持静止状态。当相对位移s=1 mm时颗粒速度增加幅度大,这是由于钢板的运动带动了与之相接触的颗粒,同时由于颗粒间相互摩擦、咬合作用,接触面处颗粒的运动会带动部分上部颗粒共同运动。当剪切位移进一步增加时,颗粒速度减小,钢板对颗粒的影响只到接触面附近约土体高度的 1/4。当相对位移s=3 mm 时,接触面处的颗粒速度开始减小,说明此时钢板的运动不再带动颗粒的运动, 颗粒只在周围颗粒的影响下发生平动或转动运动幅度很小。当颗粒不再随着钢板的运动而运动时,标准砂-钢板作用发生失效。

图12 不同位移条件下的颗粒速度矢量图Fig.12 Particle velocity vector diagram under different displacement conditions

3.4 数值模拟的应力场、位移场、速度场综合分析

对数值模拟得到的颗粒应力场、颗粒位移场、颗粒速度场综合分析,得出标准砂-钢板接触面通过颗粒的平移和转动来传递剪切应力,颗粒的位移引起接触面内土体的剪胀。

从细观数值模拟结果可看出,试验开始后钢板发生水平向位移,通过与钢板相接触的颗粒将剪切力传递至砂样中,此时与钢板相接触的颗粒主要受到两种力的作用:一是钢板对它的作用力;二是与之相接触的其他颗粒对它的作用力。在共同作用下,接触面颗粒产生3种运动状态。

(1)状态1:两种作用力的大小相等、方向相反。两种力作用在同一条作用线上时,颗粒将保持静止或匀速运动状态; 两种作用力不在同一条作用线线上时,颗粒将发生匀速转动。

(2)状态2:钢板对颗粒的作用力大于颗粒间的作用力、方向相反。两种力作用在同一条作用线上时,颗粒将沿着钢板运动方向移动,但速度小于钢板运动的速度;两种力不在同一条作用线上,颗粒将沿钢板运动方向同时发生移动和转动。

(3)状态3:颗粒间的作用力大于钢板对土颗粒的作用力。此时颗粒将沿着周围颗粒作用合力的方向发生移动或者同时发生移动和转动。

4 宏细观机理分析

从以上分析可以看出,在细观层次上观察到的接触面土体的应力、变形、位移等物理状态变化的发展趋势与宏观层次上观察到的剪应力-位移关系的发展趋势相似。这表明在标准砂-钢板相互作用的过程中,接触面土体的物理状态不断发生变化,并逐渐趋于稳定,这种物理状态的变化又导致接触面土体的力学特性发生类似趋势的变化,并表现在宏观观测到的剪应力-位移关系的响应上。

综合前文中基于应力-位移关系、土体细观组构变化、细观数值模拟对标准砂-钢板失效的分析,可以看出标准砂与钢板之间单调剪切作用时,在应力-应变关系上变现为加工硬化型,剪应力-位移关系曲线分为剪应力线性增长阶段,缓慢增长阶段和水平发展阶段,而从细观的角度考虑,土颗粒在结构物的作用力和土颗粒间的相互作用力下,表现出3种不同的运动状态,在剪应力-位移关系曲线的线性增长阶段,与钢板相接触的土颗粒的运动状态主要以静止、匀速运动或匀速转动为主,随着相对位移的逐渐增大,当接触面处大部分的土体颗粒发生随着钢板的运动而运动时,接触面处的土体将发生剪切变形,剪应力逐渐发展至峰值,对应于剪应力-位移关系曲线的剪应力缓慢增长阶段,当接触面土颗粒不再随着钢板的运动而运动时,剪应力保持不变,标准砂-钢板接触表面发生失效,对应于剪应力-位移曲线的水平发展阶段。

根据颗粒间的接触关系,颗粒的速度、接触力和位移分析,确定出标准砂-钢板单调剪切的失效机理是由于土颗粒的平移、转动,颗粒间的重新排列等所导致接触面土颗粒间的咬合摩擦、滑动摩擦大于结构物对土颗粒的作用力,使得接触面处的土颗粒不随着结构物的运动而运动,从而在土与结构物接触面产生很大的相对位移,引起失效。