基于流固耦合的离心压缩机轴系振动特性分析
2024-01-12尹燕乐许增金
尹燕乐,许增金,王 旭
(沈阳工业大学 化工装备学院,辽宁 沈阳 111000)
1 引言
离心压缩机作为典型的透平设备,被广泛应用于空分、电子半导体、纺织化纤、食品发酵、钢铁等众多领域。随之离心机转速及可靠性的提高,滑动轴承以其承载能力强、工作稳定、寿命长等优点而被广泛应用。轴承作为支撑转子系统的核心部件,其动力学特性直接影响着转子系统的转子动力学特性[1],轴承半径间隙以及有效宽度作为轴承重要的结构参数,对轴承的动静特性参数有着直接的影响[2-3]。为此,探究轴承结构参数的改变对其工作性能及转子稳定性的影响,对提高轴承-转子系统的稳定性具有重要意义。
广大学者对轴承油膜工作特性以及轴承-转子系统的耦合振动特性进行了广泛研究。文献[4]建立了轴承-转子系统动力学模型,基于有限差分法分析了不同半径间隙下的油膜特性,并进一步探究了轴承半径间隙对转子系统振动特性的影响。文献[5]采用有限体积法分析了轴承椭圆度及偏心率对油膜压力分布及转子系统稳定性的影响。Visnadi[6]考虑轴承间隙和温度对滑动轴承的影响,分析发现轴承间隙的变化对轴承稳定性的影响大于轴承温度,设计轴承参数时,应重点考虑轴承间隙的影响。文献[7]采用fluent进行了考虑温度场的滑动轴承油膜特性分析,在探究半径间隙对油膜压力特性影响的基础上推断出半径间隙对转子系统稳定性有着重要影响,但是并未进行实验或理论验证。文献[8]采用Dyrobes软件探究了预负荷系数对轴承工作特性及转子稳定性的影响规律,并在此基础上提出了一种新型周可倾瓦轴承结构。然而,这些学者均以轴承动力学特性参数为基础进行轴系动力学建模,采用combin214单元进行轴承单元模拟,鲜有学者通过油膜流场与轴系的流固耦合进行轴系的振动特性分析。为此,本文建立单油槽滑动轴承-转子系统动力学模型,首先探究轴承不同间隙比及宽径比下的油膜压力特性,进行轴承油膜与转轴的流固耦合分析探究轴承间隙比及宽径比对轴系振动特性的影响规律,分析结果可为离心压缩机轴承-转子系统参数设计提供参考数据。
2 基本理论
2.1 油膜黏温特性方程
随着转子转速的增大,轴颈与轴瓦间的油膜温度必然会逐步提高,而温度的改变也必然导致润滑油物性参数的变化,进而影响轴承的工作性能,因此,进行油膜流场仿真时,考虑温度对轴承工作特性影响是必不可少的。
本文采用的是32号液压油,根据张艳芹等[9]通过vogel黏温特性方程及液压油温度试验得到的适用于32号液压油的黏温关系式如式(1)所示
(1)
式中T--平均温度,K
μ--动力黏度,10-2Pa·s
2.2 流固耦合计算基本理论
本文采用目前流固耦合的主流计算方法进行模拟仿真,即使用不同的求解器分别求解不同的物理场,后通过流固耦合交界面完成数据的传递,这种方法的优点便是最大程度的保证了流体力学和结构力学计算程序的模块化,同时降低了求解对计算机硬件的要求。此种方法的矩阵方程可以表示为
(2)
耦合效应被[K11],[F1]对{X1}和[K22],[F2]对{X2}的依赖所解释,且至少需要两个迭代才能实现耦合响应。
3 模型构建
本文所研究压缩机转子总长为1673.5 mm,轴承支撑跨距为1340 mm,额定转速为12043 r/min,采用红套五级叶轮的单轴结构,各叶轮间装有隔套用于定位叶轮。联轴器位于转轴左侧,推力盘位于转轴右侧,两者均采用液压安装方式套装在主轴上,同时驱动侧和非驱动侧的轴承均为单油槽滑动轴承。为简化计算模型,本文采用集中质量点,极转动惯量以及直径转动惯量替代叶轮。同时,因为联轴器同时连接齿轮箱及转子,为此将联轴器一般的质量施加在转轴左端,等效参数如表1所示,转子、轴承及联轴器等均采用1Cr13材料。
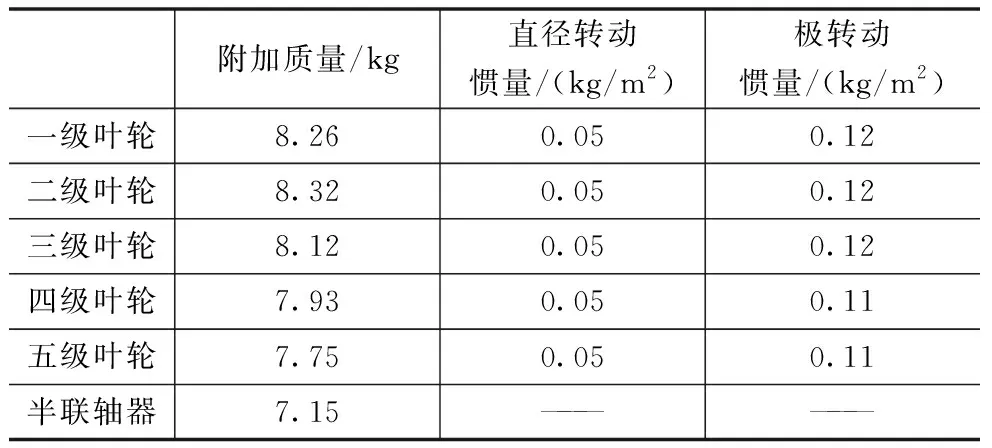
表1 叶轮质量等效参数表
4 仿真计算与结果分析
4.1 油膜流场仿真
在进行考虑油膜流场的流固耦合分析之前需先进行滑动轴承油膜流场分析。为此,首先采用spaceclaim进行轴瓦与轴颈间隙的流场填充,得到壁厚为0.0585 mm,偏心率为0.5的滑动轴承油膜三维模型,针对类似于滑动轴承油膜这种超薄壁结构,为保证网格划分质量,在此采用专门的流场网格划分软件ICEM CFD进行油膜的非结构化网格划分,径向划分为5层,周向划分为200层,轴向划分为150,得到油膜网格划分模型如图1所示。

图1 单油槽滑动轴承网格划分模型
在fluent中定义油膜材料属性如表2所示。

表2 液压油材料属性表
采用多参考系模型、MIXTURE两相流模型及层流模型进行考虑空化效应的油膜流场分析,空化压力取7550 Pa ,入口油压为0.2 MPa,油膜旋转壁面转速取12000 r/min,同时为得到更为精确的的油膜流场仿真数据,采用式(1)进行考虑黏温特性的UDF程序编写,后加载到fluent中进而得到考虑油膜温度变化下的油膜流场压力仿真结果,如图2所示。

图2 驱动侧油膜(左)和非驱动侧油膜(右)压力分布图
将油膜流场压力分布结果通过流固耦合程序施加到轴颈处。在此要特别注意,利用Workbench进行两相流混合流场的流固耦合分析时无法通过连线的方式实现流体向结构压力载荷的传递,需将fluent的结果文件导出为外部数据文件,后借助Workbench External Data模块来读取外部数据文件并进行映射关系处理进而实现流体压力载荷向结构的传递。
轴承-转子系统在工作过程中,油膜会传递给转轴一个指向轴颈圆心的向心力,其中,传递压力最大的位置即为偏心位置,此处油膜厚度最薄压力最大,以此来支撑轴颈向该方向的位移。
4.2 间隙比对轴系振动特性的影响
轴承作为影响转子系统稳定性的主要因素之一,尤其是在转子系统自身跨距较大,转速较高且尺寸小重量轻的情况下,此时的转子系统自身刚性较小,因此轴承结构参数的选择对其安全稳定运行至关重要。
在此,保持轴承-转子系统其他结构参数恒定,改变轴颈与轴瓦之间的间隙,取间隙比0.0013(0.0585 mm)~0.0019(0.0855 mm),探究随着轴承间隙比的增大,油膜压力特性及转子系统稳定性的变化规律。首先进行油膜流场仿真,探究油膜压力特性与轴承间隙间的关系,结果如图3所示。

图3 不同间隙比下的油膜压力
由图3可知,随着轴承间隙比的增大,油膜压力逐渐减小。且随油膜厚度增加,油膜压力逐渐趋于稳定值。
接下来进行单向流固耦合分析,探究间隙比为0.0019时,转子各阶模态振型如图4所示。

图4 轴系前4阶模态振型
根据API 617准则,我们只需要关注额定转速以下及其高一阶的临界转速即可,得到随轴承间隙变化的轴系临界转速变化规律如表3所示。
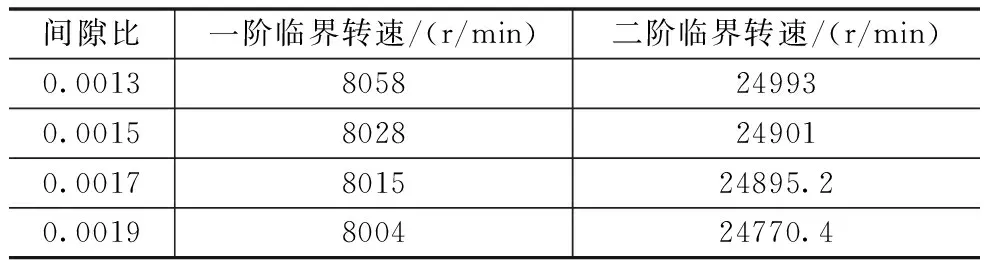
表3 不同间隙比下的轴系临界转速
由表3可知,离心压缩机轴系的临界转速随着轴承间隙比的增大而减小,但减小幅度很小,间隙比从0.0013增至0.0019,轴承的一阶临界转速仅减小0.67%,二阶临界转速仅减小0.89%。
接下来探究轴承间隙比对振动幅值的影响,结果如图5所示。

图5 不同间隙比下的轴系共振振幅
由图5可知,轴系振动幅值随轴承间隙比的增大呈现先减后增的趋势,且增幅也在逐步增大。这是因为在油膜厚度增加到一定值时,油膜的切向力增大而阻尼力减小,切向力所做的正功大于阻尼力所做的负功,进而导致油膜失稳,进而导致振动幅值剧增,该分析结果与文献[10]相似。结合表3和图5可知,轴承间隙对转子系统的共振频率影响不大,主要影响了转子系统的稳定性,因此只有选择合理的轴承半径间隙才能保证离心压缩机高速安全稳定的运行。
4.3 宽径比对轴系振动特性的影响
轴承宽径比是影响转子系统稳定性的另一重要轴承结构参数,为此本节探究了轴承宽径比分别为0.55、0.6、0.65、0.7、0.75、0.8六种轴承结构参数下,转子系统的振动稳定性。
首先探究不同宽径比下油膜压力特性的变化规律如图6所示。
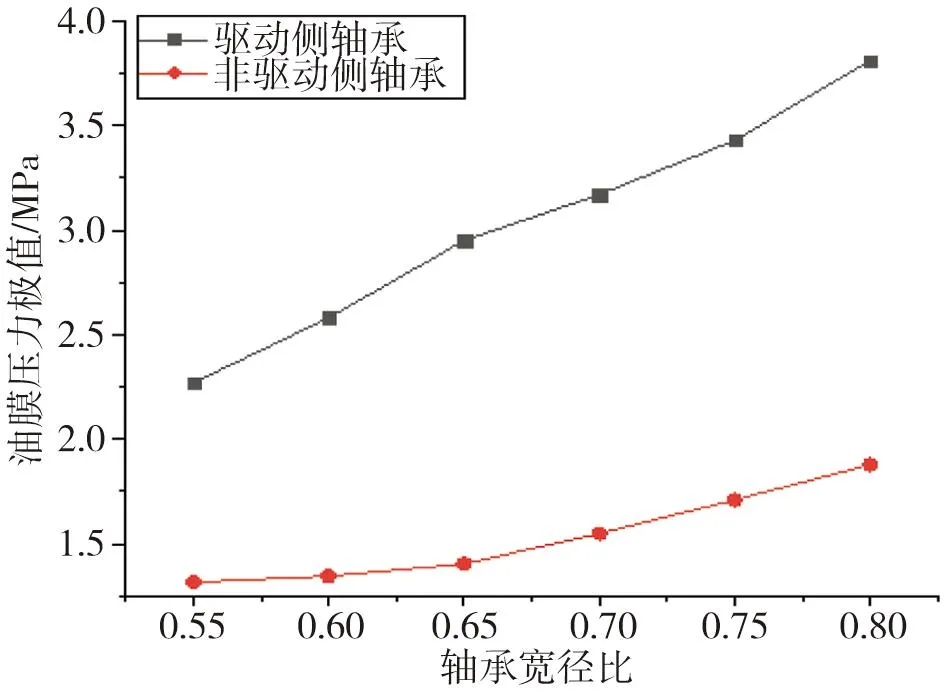
图6 不同宽径比下的油膜压力
由图6可知,滑动轴承的油膜压力会随着轴承宽径比的增大而增大。这是因为轴承的宽度越小,液压油从轴承两端流出的就越多。进而导致油膜压力也随之下降。
随后探究不同宽径比对轴系临界转速的影响规律,结果如表4所示。

表4 不同宽径比下的轴系临界转速
由表4可知,轴系一二阶临界转速均随轴承宽径比的增大而略有增大,但增幅较小,宽径比由0.55增至0.8,轴系一阶临界转速提高3.6%,二阶临界转速提高6.9%。
轴系的稳定性随轴承宽径比的增大呈现如图7所示的变化规律。

图7 不同宽径比下的轴系稳定性
由图7可知,离心压缩机轴承-转子系统的稳定性并没有随着宽径比的增减而呈现出规律性的上升或下降趋势,这也就意味着我们需要根据离心压缩机的实际工况选择长径比合适的轴承,且本文所研究的转子系统采用轴承宽径比为0.8时,轴系稳定性最好。
5 结论
(1)通过探究轴承间隙比对油膜压力特性及轴系稳定性的影响规律发现:随着轴承间隙比的增大,油膜压力递减,且减小趋势逐渐趋于平缓;轴系临界转速随轴承间隙比的增大而减小,但减小幅度可忽略,间隙比从0.0013增至0.0019,轴系的一阶临界转速仅减小0.67%,二阶临界转速仅减小0.89%;轴系的共振振幅随轴承间隙比的增大呈现出先减后增的趋势,本文所研究转子系统采用间隙比为0.0014的轴承最为合适,在0.0014处振动幅值最小,稳定性最好。
(2)通过探究轴承宽径比对油膜压力特性及轴系稳定性的影响规律发现:随轴承宽径比的增大,油膜压力逐步增大;轴系临界转速随随轴承宽径比的增大而增大,宽径比从0.55增至0.8,轴系一阶临界转速增幅为3.6%,轴系二阶临界转速增幅为6.9%;轴系的各阶振幅并未随宽径比的增减而呈现规律性变化,这就需要我们根据旋转机械实际工况进行选择,本文所研究转子系统采用宽径比为0.8的轴承最为合适。
