HTPB推进剂细观损伤及载荷传递行为数值模拟①
2024-01-12逯晗斗胡松启于庆民白帅帅刘殊远
逯晗斗,陈 雷,胡松启,于庆民,3*,白帅帅,刘殊远
(1.西北工业大学 力学与土木建筑学院,西安 710129;2.西北工业大学 航天学院,西安 710072;3.西北工业大学 航空学院,西安 710072)
0 引言
固体推进剂作为一种典型的颗粒填充复合材料,推进剂的宏观力学性能强烈依赖于细观结构。虽然固体推进剂类似颗粒增强复合材料,但不同的是,推进剂中的颗粒并不都是起增强作用,颗粒含量增加反而会导致材料更容易受到不可避免的破坏。目前,已有许多国内外学者采用试验和数值的方法对推进剂在细观尺度下的损伤进行了深入研究。VAN RAMSHORST等[1]基于扫描电子显微镜(SEM)研究了固体推进剂细观形貌与宏观变形破坏的关系,发现载荷作用下颗粒/基体界面脱粘,裂纹沿颗粒/基体界面生长。史佩等[2]基于分子动力学算法建立了具有高体积分数(60%左右)的固体推进剂颗粒填充模型,在此基础上进行的细观力学分析可以有效地考虑固体推进剂细观结构对其力学性能的影响。李高春等[3]通过Mori-Tanaka方法将小颗粒和基体等效,然后模拟了大颗粒和等效基体之间的相互作用及“脱湿”损伤,得到的推进剂模量和试验结果吻合。封涛等[4]建立了具有不同细观结构的推进剂模型,发现大粒径AP颗粒界面更容易脱粘,RDX颗粒的界面损伤不明显,其含量增加会降低初始模量。张建伟等[5]根据有限元理论及细观力学均匀化方法研究了颗粒体积分数对推进剂模量的影响,说明了填充颗粒的增强作用主要体现在瞬时模量上。LI等[6]研究了细观结构的力学性能和推进剂中初始界面缺陷对宏观力学影响的相关性。职世君等[7-9]通过在推进剂颗粒/基体界面处引入双线性内聚力模型,研究了填充颗粒的含量、粒径和位置分布等细观特征对推进剂宏观力学性能的影响。另外,张文普等[10]用空气泡代替了颗粒,根据模量随应变变化的趋势,认为推进剂模量下降的主要影响因素是界面“脱湿”。FRANCQUEVILLE等[11]为了深入了解推进剂本构与局部损伤、宏观力学行为之间存在的关系,通过单轴拉伸实验,研究了推进剂应力-应变响应、体积变化,并根据受载条件下的扫描电镜图像,对局部损伤进行了定性描述,同时通过数值模拟讨论了粘聚区参数与局部损伤萌生、演化以及粘结行为与非均质材料宏观力学响应之间的关系。以上研究主要集中于颗粒“脱湿”这一现象的描述以及讨论细观结构、界面参数等变量对推进剂宏观力学性能的影响,而未考虑颗粒形状对推进剂力学性能的影响,同时缺少对颗粒和基体之间载荷传递能力的定量表征和分析。
为了深入了解固体推进剂细观损伤的原因以及量化细观结构对力学性能的影响,本文首先通过中心框增长法确定了具有一定细观特征的推进剂的最佳RVE尺寸,并利用应力集中因子及载荷传递系数[12]概念,基于双线性内聚力模型和粘超弹本构,研究了颗粒形状、大颗粒含量以及颗粒体积分数对应力集中和载荷传递系数的影响,这对揭示复合固体推进剂细观结构组成与宏观力学行为关系、量化固体推进系统的长期可靠性至关重要。
1 HTPB推进剂各组分材料模型
固体推进剂作为一种典型的多相复合材料,其连续相基体是一种高分子聚合物,具有较好的力学性能和较小的粘度,能够容纳大量的固体颗粒;分散相由AP颗粒和Al颗粒组成,为固体推进剂提供能量;界面相发生“脱湿”是导致推进剂宏观断裂的主要原因。本文基于三相结构(连续相-界面相-分散相)建立了固体推进剂的细观损伤模型。
1.1 粘超弹本构模型
HTPB固化胶片经过单轴拉伸加载和卸载试验后,如图1所示,完全卸载后,应变并未恢复至0,主要是由于HTPB中的大分子链储存的应变势能,使得卸载阶段的斜率明显小于初始阶段,大于软化阶段。根据其力学响应,基体具有超弹性和不可恢复的粘弹特性。因此,在建立本构模型时,需要同时考虑超弹特性和粘弹特性。
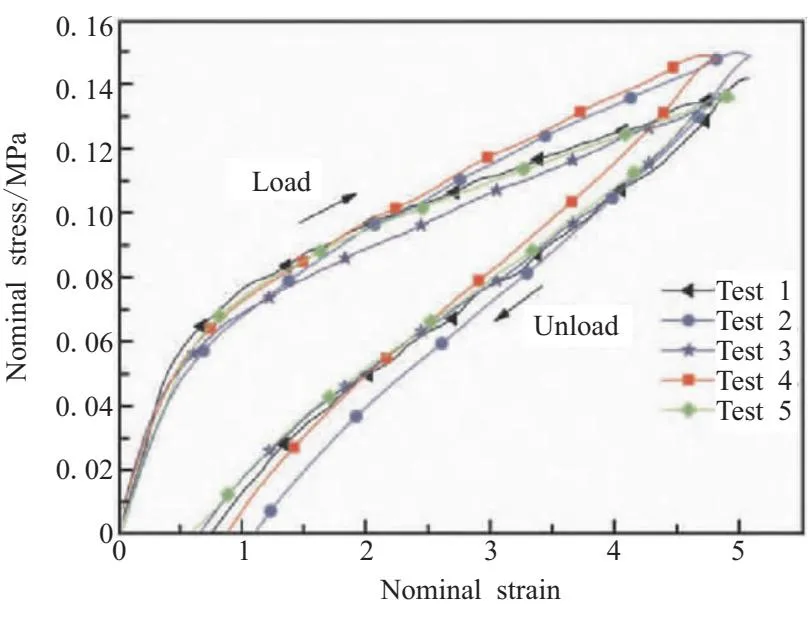
图1 加-卸载名义应力-应变实验曲线[13]
选择Ogden应变能函数描述推进剂基体的超弹性力学响应:
(1)
式中λi为主伸长率;μi、αi为材料参数;Dk为不可压缩参数;J为变形后与变形前的体积比,对于不可压缩材料,J=1。
结合式(1),可以获得Ogden超弹性模型关于应力-应变的表达式:
(2)
广义Maxwell模型可以表征固体推进剂静态粘弹特性,在ABAQUS中,常用Prony级数形式来表示:
(3)
式中E∞、Ei和τi分别为平衡模量、第i个Maxwell单元的松弛模量和松弛时间;t为时间。
基于上述粘超弹性理论,Prony级数和Ogden超弹性模型的相关系数如表1和表2所示。

表1 HTPB基体松弛模量主曲线Prony级数的各阶系数[14]

表2 HTPB基体3阶Ogden超弹性模型[15]
1.2 分散相颗粒材料参数
固体推进剂中分散相颗粒模量及强度远远高于基体,准静态加载过程中,不考虑AP和Al颗粒的损伤,将颗粒视为弹性材料[11]。Al颗粒数量巨大且粒径较小,为了降低计算收敛难度,本文的数值模拟中仅考虑AP颗粒[16],且假定不同粒径的AP颗粒材料参数一致,AP颗粒的弹性模量为19.5 GPa,泊松比为0.25。
1.3 双线性内聚力模型
颗粒和基体的“脱湿”损伤是推进剂断裂失效的主要原因,一般通过内聚力模型描述界面的损伤。其中,双线性内聚力模型形式简单,使用最为广泛。在实际情况下,需要采用混合模式准则来判断界面的损伤起始点。目前,比较常用的初始损伤准则是二次应力准则,其表达式如下:
(4)
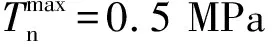
达到界面损伤起始准则后,界面开始出现损伤,损伤变量D表示为
(5)
式中D的取值范围为[0,1],当D=0时表示界面未出现损伤,当D=1时表示界面完全失效,模拟的裂纹面完全分离。
当界面损伤开始演化时,界面刚度会随之减小,界面刚度与损伤变量的具体关系如式(6)所示:
(6)

当界面等效位移达到0.02 mm时[17],界面完全失效。为了保证计算的收敛性,在不影响计算结果的基础上对界面内聚力单元引入适当的粘性[18]。
2 HTPB推进剂细观数值模型
2.1 RVE尺寸确定
细观力学模型主要利用均匀化技术,从材料的局部本构响应来确定宏观材料参数。均匀化技术已广泛应用于预测材料宏观响应的微尺度数值结果,均匀化通常是基于代表性体积单元的概念。一方面,RVE尺寸要足够大,使其可以代表整个宏观模型的力学性能;另一方面,RVE尺寸过大会造成计算资源极大的浪费,同时也不利于有限元计算的收敛。因此,在建模时应该考虑RVE尺寸的下界,选择合适的RVE尺寸。
依照经验法一般选择最大颗粒尺寸的3~5倍[19],可选取的RVE尺寸范围太大,且由于推进剂材料的特殊性,无法满足一些精确计算。本节采用数值方法定量分析了RVE尺寸。为提高计算可靠性,基于目前推进剂配方,建立的模型如图2所示,其中,模型的RVE尺寸为4000 μm×4000 μm,大颗粒(红色)粒径为250~425 μm,体积分数为39.94%,小颗粒(蓝色)粒径为106~150 μm,颗粒体积分数为22.7%。

图2 RVE尺寸细观模型
采用均匀位移边界(后续章节有对均匀位移边界条件的具体说明)对上述进行单轴拉伸5%。图3是覆盖渐增中心方框的单轴拉伸5%细观模型应变场。如图所示,采用中心框增长法[20]确定RVE尺寸,该方法使用从应变场中心点生长的单个方框,方框尺寸记为R,研究方框内平均应变随方框尺寸增长的变化规律。然后通过评估平均应变在一定范围内的收敛性来确定RVE尺寸。为了定量分析RVE尺寸,将方框内的局部平均应变记作εlocal,整个模型的全局平均应变记作εmacro,则方框内应变变化:
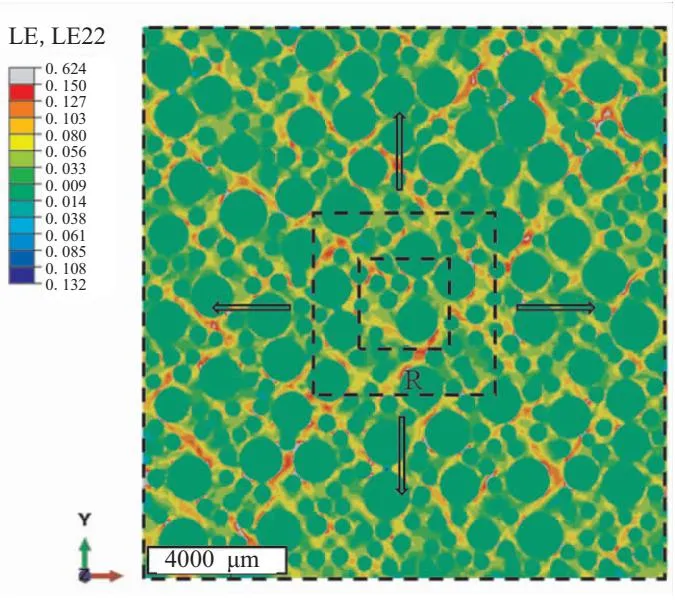
图3 覆盖渐增中心方框的细观模型应变场
(7)
图4给出了模型应变变化参数随方框尺寸变化曲线。从图4中可以看出,随着方框尺寸的增大,局部平均应变接近于施加的全局应变,在较低的方框尺寸下,局部平均应变与全局应变相差较大。依据5% Strain variation和1% Strain variation将Box size划分为3个不同的区域,分别记为Ⅰ、Ⅱ和Ⅲ。在区域Ⅰ(R<1330 μm)中,随着方框尺寸的增大,应变变化参数呈振荡趋势;在区域Ⅱ(1330 μm

图4 平均应变随方框尺寸的变化曲线
另外,方框尺寸增加到模型的边界时,其平均应变变化参数有略微变大的趋势,主要是施加的边界条件的干扰。最后,将使用中心框增长法估算的RVE尺寸与经验选取RVE尺寸进行比对,依据经验一般选择最大颗粒尺寸的3~5倍[19],RVE尺寸选取范围过大且因推进剂材料的特殊性,无法满足一些精确计算。如表3所示,结果较为接近,说明了采用中心框增长法估算的RVE尺寸可行性。

表3 不同方法确定RVE尺寸
2.2 边界及载荷
图5为均匀位移边界条件以及周期性边界条件。图6为不同模型不同边界条件下拉伸方向应力分布,给出了单颗粒模型和多颗粒模型分别在两种边界条件下,沿加载方向应力分布云图。对于复杂的多颗粒模型,不同边界条件下颗粒发生“脱湿”损伤的位置几乎一样,其拉伸方向的最大应力略有差别,均匀位移边界条件下最大应力为20.972 MPa,周期边界条件下最大应力为23.476 MPa;对于单颗粒,应力分布完全一致。
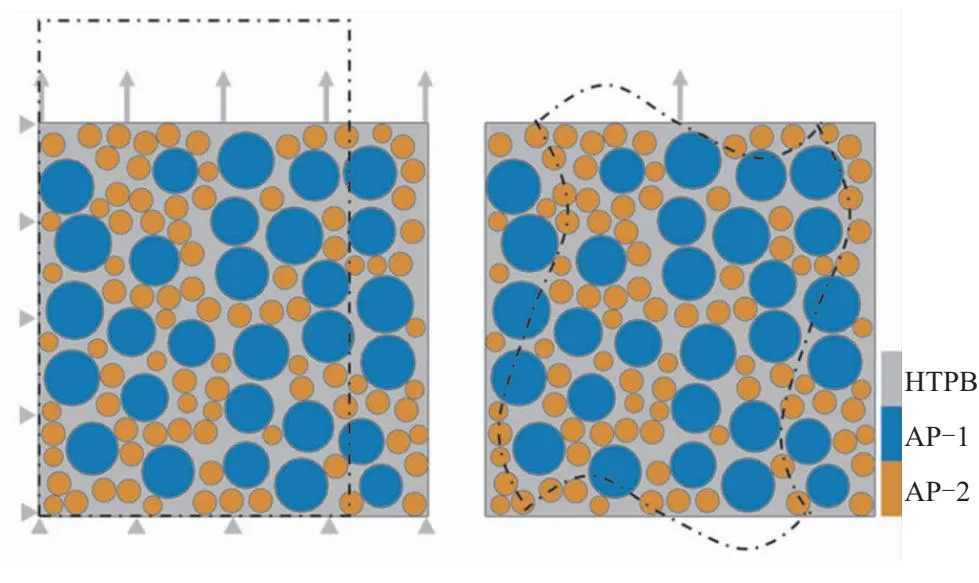
(a) Uniform displacement boundary conditions (b)Periodic boundary condition

图6 不同模型不同边界条件下拉伸方向应力分布
图7为不同模型不同边界条件应力-应变曲线。对于单颗粒模型,不同的边界条件对应的应力-应变曲线基本吻合;而多颗粒模型中,由于颗粒脱粘的位置具有一定的随机性,因此不同的边界会造成一定的误差,但仍然小于5%,可以认为两种边界条件不会造成计算结果较大差异。

图7 不同模型不同边界条件应力-应变曲线
对于拥有复杂细观结构的推进剂而言,依赖周期性网格实现周期性边界条件是十分困难的。因此本文选择施加较为简便的均匀位移边界条件,如图5(a)所示,仅需对模型下边界节点和左边界节点的竖直方向自由度和水平方向自由度分别进行约束,右边界通过方程约束使其保持平直,同时对上边界节点施加竖直方向位移,上边界节点施加均匀位移载荷。
2.3 二维颗粒填充模型建立
HTPB复合固体推进剂的颗粒填充质量分数通常高达60%~80%,同时颗粒粒径满足一定的尺寸分布。图8为HTPB推进剂微CT扫描重构图、包含所有颗粒的全配方推进剂细观模型。

(a) Real mesoscopic structure[22] (b) Filling model with small particles(Volume
从图8(a)可以看出:AP颗粒的形状大多接近圆形或椭圆形,在基体中高密度填充,且具有较大的尺寸跨度但大尺寸AP颗粒数量较少;Al颗粒形状近似为圆形,其尺寸远小于AP颗粒,且填充在AP颗粒之间,均匀分散在基体相之中;部分颗粒的边缘及内部含有微孔洞。
常用的建立固体推进剂颗粒填充模型的方法主要有随机吸附算法(Random Sequential Algorithm,RSA)和分子动力学(Molecular dynamics,MD)算法。另外,COLLINS等[23]基于微CT扫描,结合数学统计重构了推进剂细观结构,该方法可以最大程度还原固体推进剂真实形貌,但普适性不好,无法对细观结构这一变量进行讨论。本文通过DIGIMAT软件,结合真实的HTPB推进剂细观模型,高效、准确地建立了如图8(b)所示的推进剂细观模型,AP颗粒粒径采用二级配,各组分及尺寸如表4所示,粘合剂及其他助剂等效到HTPB中。将所建模型导入到ABAQUS软件中,二维细观颗粒填充模型视为平面应变问题进行数值求解[24],进行赋予各组分力学性能参数、有限元网格划分、施加2.2节中图5(a)所示的均匀位移边界条件等前处理工作,之后开始有限元分析计算。
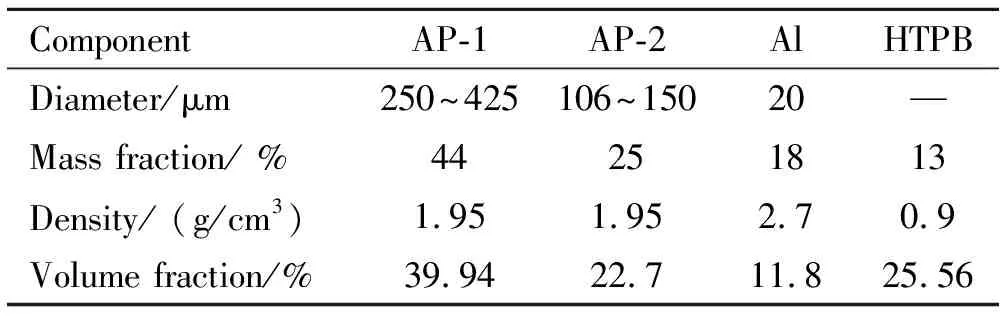
表4 HTPB推进剂基本配方及尺寸[21]
2.4 应力-应变均匀化
采用直接均匀化的方法,通过Abaqus-Python脚本获取所有积分点的应力和应变,以及对应的体积或面积权重,则RVE平均应力和平均应变的分别定义为:
(8)
(9)
式中 上标t表示三角形单元,q表示四边形单元;V为代表体积元的体积;σij、εij分别为积分点处的应力和应变;N为单元数量;Vt、Vq为单元的体积。
根据颗粒复合材料的强化机理,颗粒对基体的直接影响是通过两者之间的载荷传递过程来实现的。首先,颗粒、基体和复合材料的平均应力分别为σp、σm、σc,进而定义颗粒的应力集中因子Rp=σp/σc,基体应力集中因子Rm=σm/σc,用于表征组分材料的平均应力集中程度。类似地,为了定量描述颗粒和基体之间的载荷传递行为,可定义载荷传递系数为Rp/m=σp/σm。
3 结果讨论
颗粒位置的分布具有一定的随机性,为了研究颗粒位置对计算结果的影响,结合HTPB推进剂的配方及填充颗粒尺寸分布规律,建立了4组具有不同颗粒位置分布的细观模型,填充体积分数均为62.7%。
由于模型数量较多,仅展示了其中3个随机模型在不同拉伸阶段的刚度下降率(SDEG)云图分布(SDEG为0表示界面未发生损伤,SDEG为1表示界面单元完全失效,并删除失效单元),如图9所示。可以看出,大颗粒决定了损伤最先发生的位置,从宏观角度来看,不同模型大颗粒所占的体积分数是一致的,界面Cohesive单元包含的比例也一致,因此宏观力学性能也几乎一致。但是颗粒位置改变,最先失效的单元位置也随之改变,如图9(b)所标注的,颗粒位置的随机导致界面单元失效的随机性,但失效的进程并未受到影响,当外载应变为9.74%时,不同模型几乎同时出现界面单元失效。如图9(c)所示,当应变达到20.31%时,大部分大颗粒和极少数小颗粒都与基体发生脱粘,由于颗粒之间复杂的相互作用导致了极少数小颗粒界面“脱湿”,这进一步说明了“脱湿”损伤发生在大颗粒界面或颗粒聚集的地方,小粒径颗粒主要起增强作用,基本不发生“脱湿”损伤。值得注意的是,颗粒位置改变虽然不会影响推进剂宏观力学性能,但导致空穴出现的位置发生了改变,从而影响了裂纹扩展的路径。

(a)Strain 5.33%
图10给出了4组随机颗粒位置模型的应力-应变曲线。可以看出,在弹性阶段,应力-应变曲线完美重合,计算结果波动几乎为0,表明在颗粒级配和体积分数相同的情况下,在“脱湿”损伤前,材料的力学性能不会受到颗粒位置改变的影响;“脱湿”损伤发生阶段,应力出现下降,主要是界面单元逐渐失效,不再承受拉伸载荷,从而导致了应力曲线快速下降,由于颗粒位置不同,发生“脱湿”损伤的位置也不同,计算的结果稍有波动,但最大波动也仅5%,可以认为总体上不存在明显的差异;当应变达到15%以后,主要是基体承载阶段,应力-应变曲线逐渐汇聚靠拢。

图10 不同模型应力-应变曲线
图11给出了随机模型在不同加载阶段的面积变化率。在弹性阶段,即应变为5.33%时,不同随机模型下面积变化率(S-S0)/S0基本一致,其中S0代表RVE模型初始面积(如图5(a)实线方框所示),S表示拉伸变形后的面积(如图5(a)虚线方框所示);当拉伸应变为20.31%时,颗粒位置影响了“脱湿”的位置,导致面积变化率略有差别,如Model 1面积变化率约为18.87%,Model 2的面积变化率约为18.23%,两者的相对误差仅为3.5%。
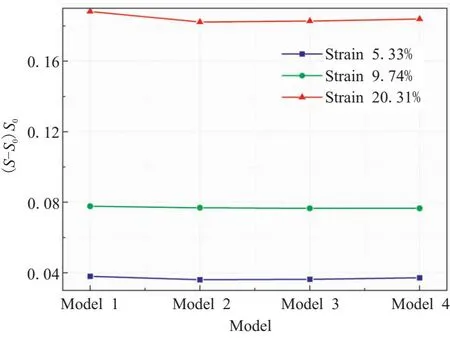
图11 不同模型的面积变化率
由此可知,当颗粒的体积分数和颗粒级配一定时,改变颗粒的位置不会对结果产生较大影响,因此在后文的计算中可忽略颗粒位置对结果的影响。
3.1 颗粒形状对推进剂力学性能的影响
固体推进剂的颗粒并不是理想化的圆形,麦麦提图尔荪等[25]对多边形颗粒填充细观模型进行数值计算,发现多边形在突出的顶点附近容易产生应力集中现象,容易造成基体撕裂,因此实际生产过程中一般都会采用较为圆润的颗粒。本节仅考虑了椭圆形颗粒,研究了相同体积分数下,颗粒的长径比(Ap)对固体推进剂力学行为的影响,其中不同形状的颗粒都是随机分布的。
颗粒长径比越大,显然越容易发生应力集中现象。图12(a)给出了应变为20%时,不同长径比颗粒的最大主应力云图分布。长径比增加一倍,颗粒的最大拉伸主应力从1.051 MPa增加到1.209 MPa,增幅约为15%;压缩主应力从0.16 MPa增加到0.238 MPa,增幅接近50%。对基体采用同样的研究方法。图12(b)给出了应变为20%时,不同长径比基体的最大主应力分布,当长径比Ap=1.0时,基体的最大主应力为16.679 MPa;当长径比Ap=2.0时,最大主应力增加到了29.013 MPa,增幅约为74%。
通过载荷传递系数,可以有效地表征不同长径比的颗粒载荷传递的效率。图13给出了不同长径比下,载荷传递系数的变化趋势。

图13 长径比对载荷传递系数的影响
由图13可以看出,在初始阶段,载荷传递系数基本保持不变,长径比越小,载荷传递系数越高,表明越圆润的颗粒越有利于载荷传递;同样的,载荷传递效率越高,界面单元也就越容易发生损伤。当长径比Ap=1.0时,平均载荷传递系数Rp/m最先开始下降,下降速率也是最快的,主要是初始阶段高效率的载荷传递导致界面单元失效的数量最多,界面单元失效后不再承载,从而降低了载荷传递效率。长径比Ap=2.0时,初始阶段载荷传递效率最低,但同样却阻止了界面单元的快速损伤,在应变大于10%以后,未失效的界面单元的数量最多,反而提高了模型的载荷传递效率。
3.2 颗粒级配对应力集中和载荷传递系数的影响
为了考虑颗粒级配对应力集中程度和载荷传递效率的影响,分别建立了3个不同的细观计算模型,如图14所示,模型体积分数都为42.7%。其中,f表示模型的体积分数,下标AP-1表示大颗粒,粒径250~425 μm,呈正态分布;AP-2表示小颗粒,粒径为150 μm。

(a)Model 1 (b)Model 2 (c)Model 3
加载过程中,不同级配下颗粒和基体应力集中因子的变化趋势如图15所示。可以看出,对于颗粒来说,其应力集中因子Rp在加载的最初阶段基本保持不变,而后下降速率开始增大,最后下降速率又开始变缓。基体的应力集中因子Rm的变化趋势与颗粒正好相反,即加载的最初阶段基本保持不变,而后上升速率开始增大,最后上升速率又开始变缓。同时,大颗粒含量越高,在初始阶段颗粒的应力集中程度越大,脱粘后颗粒的应力集中程度越小;初始阶段基体的应力集中程度越小,脱粘后基体的应力集中程度越大。以全是大颗粒的模型为例,随着“脱湿”的进行,颗粒的应力集中因子先下降,而后趋于平稳,整体下降的速率逐渐增加而后逐渐减慢,最后颗粒应力集中因子趋于0,表明此时基体的应力几乎无法传递到颗粒中,整个模型的平均应力基本上和基体等效。
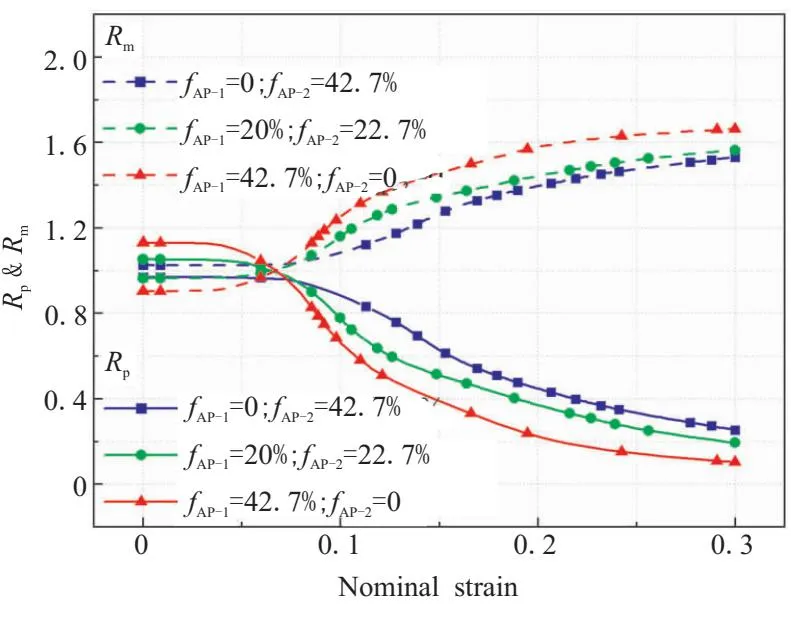
图15 不同级配对应力集中因子的影响
图16给出了不同颗粒级配下,载荷传递系数的变化关系。在初始阶段,载荷传递系数不会随外加载荷的变化发生改变,大颗粒体积分数从0增加至42.7%时,载荷传递系数也从0.95增加至1.25,表明初始阶段大颗粒含量增加可以提高载荷传递效率;随着应变的增加,仅含大颗粒模型的载荷传递系数开始迅速减小,而不含大颗粒模型的载荷传递系数变化不大。载荷传递系数下降主要原因是界面单元损伤发生失效从而无法传递载荷,表明大颗粒含量越多,其界面损伤的进程越快,同时界面损伤程度越剧烈,大颗粒更容易脱粘,脱粘以后载荷传递比较困难,所以曲线下降更快;随着拉伸应变的进一步增加,载荷传递系数进入平缓下降阶段,当应变为0.3时,仅含有大颗粒模型的载荷传递系数接近0,表明大颗粒/基体界面大部分单元均已失效不再承载,大颗粒含量越高,界面“脱湿”损伤也越严重。

图16 不同级配对载荷传递系数的影响
3.3 颗粒体积分数对应力集中和载荷传递系数的影响
针对颗粒体积分数对复合材料内部载荷传递行为的影响,以颗粒长径比为1.0的情况为例进行研究。结合推进剂颗粒级配关系,生成3组不同体积分数的推进剂细观填充模型,模型对应的体积分数分别为22.7%、42.7%和62.7%,如图17所示。

(a)fAP=22.7% (b)fAP=42.7% (c)fAP=62.7%
不同颗粒含量时,颗粒和基体应力集中因子随外加应变的变化规律如图18所示。从图中可以看出,“脱湿”前颗粒和基体的应力集中因子差距较小,都在1.0附近;当应变达到0.1后,随着颗粒含量的提高,颗粒和基体的应力集中因子都将逐渐增加,这是因为颗粒体积分数的变化,会在较大程度上改变复合材料的平均应力。以应变为30%的阶段为例进行分析,当颗粒体积分数很小时,颗粒的应力集中因子也很小,如图体积分数为22.7%时,颗粒的应力集中因子接近0,复合材料的平均应力将会更接近于基体的平均应力,同时基体的应力集中因子也将更接近于1.0;而当颗粒体积分数很大时,复合材料的平均应力将更接近于颗粒,因此颗粒的应力集中因子将趋近于0.5,而同时基体的应力集中因子接近2.0。
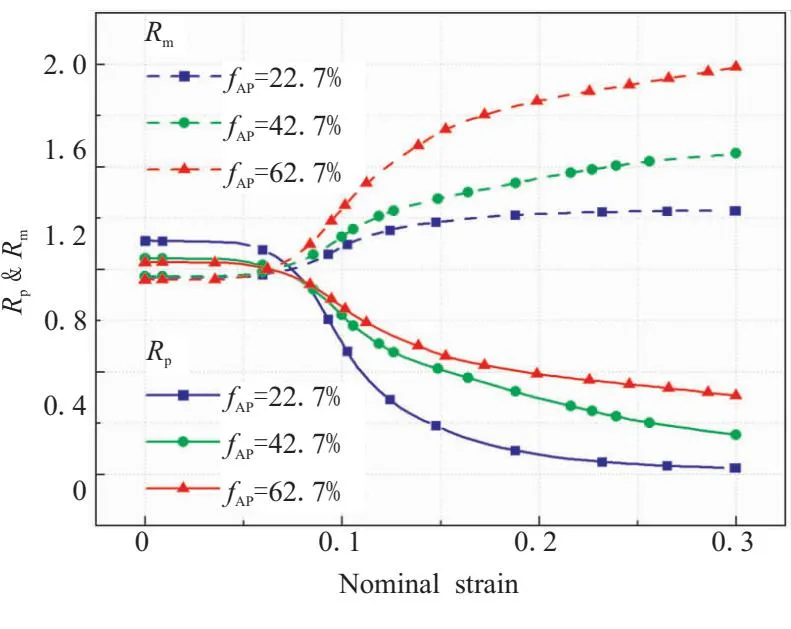
图18 不同体积分数对应力集中因子的影响
体积分数对载荷传递系数的影响如图19所示。在初始阶段,颗粒体积分数越大,载荷传递系数越小,表明初始阶段体积分数增加会降低载荷传递的效率;当拉伸应变约0.05时,载荷传递系数开始下降,和改变颗粒级配不同的是,体积分数发生改变,并不会影响损伤的进程,载荷传递系数几乎同时下降,但会影响其下降的速率。体积分数fAP=22.7%的载荷传递系数下降最快,下降幅度最大,当应变达到30%时,载荷传递系数从初始1.2下降至0,表明此时界面损伤严重,应力无法通过基体传递颗粒;而当体积分数fAP=62.7%时,载荷传递系数最大值和最小值的差值明显小于较低体积分数的情况。在基体承载阶段,体积分数越低,其载荷传递系数的变化越平缓,主要是因为体积分数越低,界面相的占比也就越少,当大部分单元发生“脱湿”损伤后,阻止了颗粒和基体之间的载荷传递,此时颗粒的平均应力接近0,RVE模型的平均应力和基体的平均应力接近。
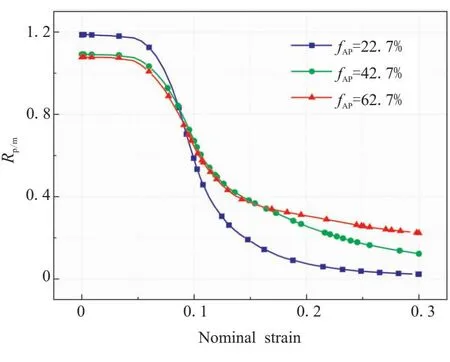
图19 不同体积分数对载荷传递系数的影响
4 结论
本文基于粘超弹性本构和双线性内聚力模型对HTPB固体推进剂进行了数值模拟,研究了推进剂细观损伤和载荷传递特性,得到以下结论:
(1)相较于经验法,采用中心框增长法确定的RVE尺寸更为精确、合理;颗粒位置随机并不会对RVE模型的力学性能造成明显的影响,这也进一步验证了采用RVE模型来代表宏观推进剂的可靠性,但会改变空穴出现的位置,从而影响了裂纹扩展的路径。
(2)颗粒的长径比越大,初始阶段载荷传递效率越低,从而阻止了界面单元的快速损伤;相同体积分数下,由于大颗粒的界面处更容易发生“脱湿”损伤,随着载荷的增加,推进剂的应力值及载荷传递系数下降得更快。
(3)体积分数发生改变,并不会影响损伤的进程,但会影响载荷传递系数下降的速率;颗粒填充体积分数主要影响着推进剂基体的承载能力,颗粒的体积分数越低,相应基体的占比则越大,在“脱湿”后,RVE平均应力就越接近基体的平均应力。
致谢:本研究得到了173计划基金(2021-JCJQ-JJ-0401)、中央高校基本科研业务费(D5000210602)及西安近代化学研究所创新合作项目(SYJJ200313)等资助,在此表示感谢!
