利用基本图形法构造中点辅助线

张强

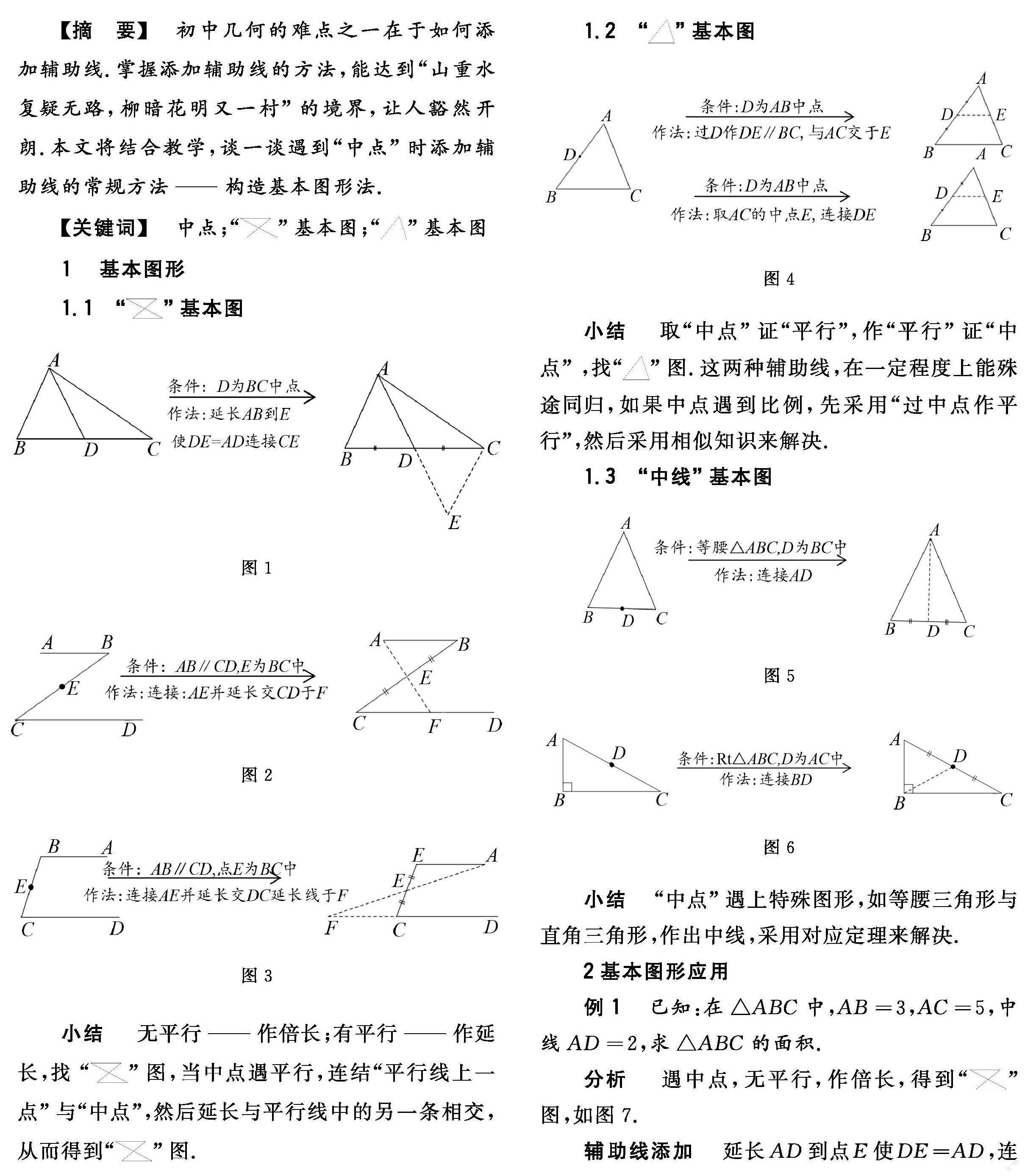
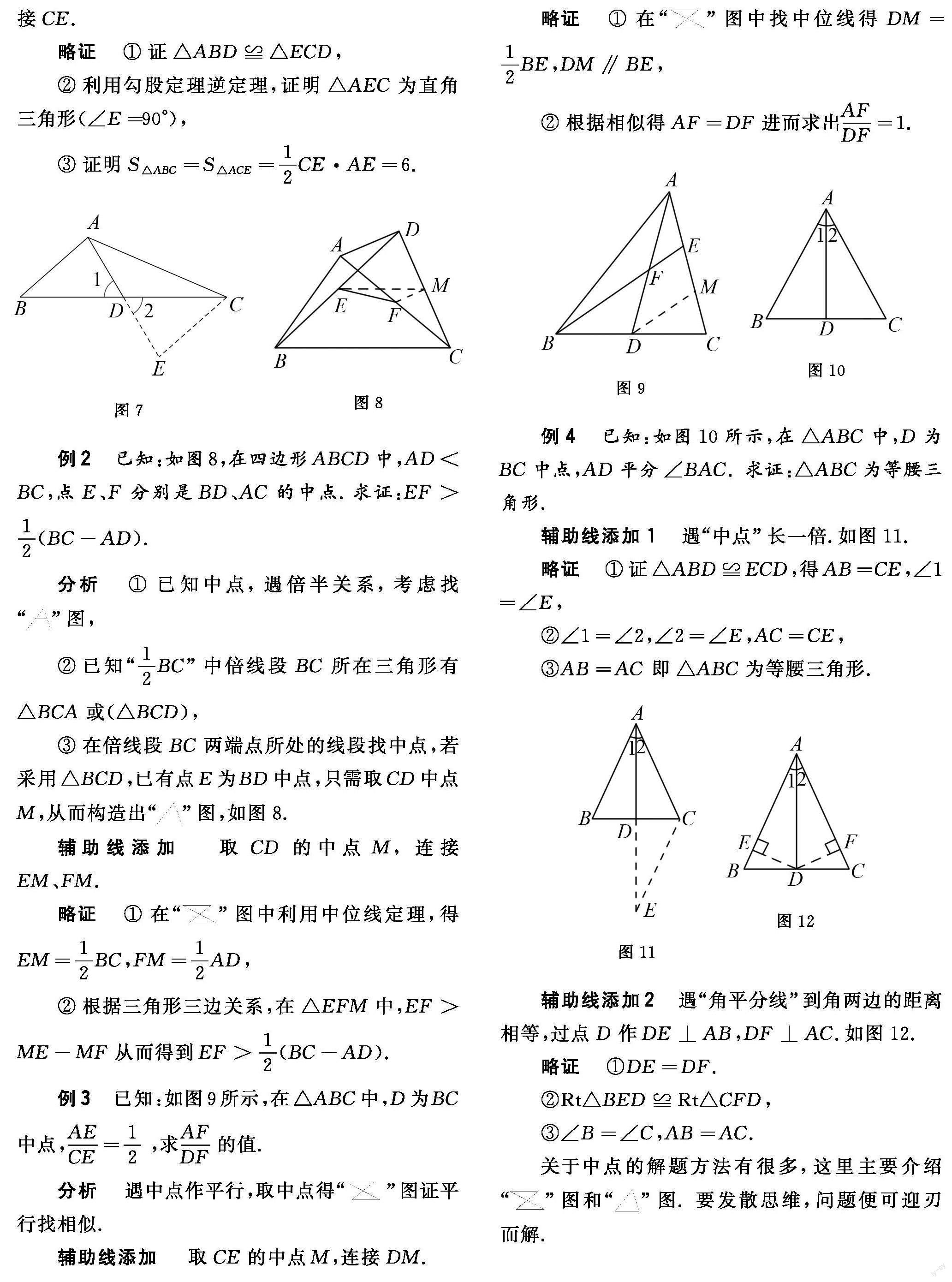
【摘  要】  初中几何的困难之一在于如何添加辅助线，掌握辅助线添加方法，从而达到“山重水复疑无路，柳暗花明又一村”的境界，让人豁然开朗.结合教学，谈一谈，遇到“中点”，添加辅助线的常规方法——构造基本图形法.

【关键词】  初中数学；遇中点；“中线”基本图

1  基本图形

1.1  “     ”基本图

小结  无平行——作倍长；有平行——作延长，找 “     ”图，当中点遇平行，连结“平行线上一点”与“中点”，然后延长与平行线中的另一条相交，从而得到“     ”图.

2  “    ”基本图

小结  取“中点”证“平行”，作“平行”证“中点” ，找“    ”图.这两种辅助线，在一定程度上能达到殊途同归，如果中点遇到比例，先采用“过中点作平行”，然后采用相似知识来解决.

3  “中线”基本图

小结  “中点”遇上特殊图形等腰三角形与直角三角形，作出中线，采用对应定理来解决.

2  基本图形应用

例1  已知：在中，，，中线，求的面积.

分析  遇中点，无平行，作倍长，得到“    ”图，如图7.

辅助线添加  延長到点使，连接.

略证  ①证；

②利用勾股定理逆定理，证明，

③.

例2  已知：如图8，在四边形中，，分别是的中点.求证：.

分析  ①已知中点，遇倍半关系，考虑找“    ”图.

②由“”倍线段所在三角形有（或）.

③在倍线段两端点处的线段找中点，若采用，已有为中点，只需取中点，从而构造出“   ”图，如图8.

辅助线添加  取的中点，连接.

略证  ①在“   ”图中利用中位线定理，

得，

②根据三角形三边关系，在中，，

从而得到.

对于中点的解题方法很多，这里主要介绍“   ”图和“   ”图. 要打开思维，问题便可迎刃而解.