关于动圆问题破题方法的举例探究

李平

【摘  要】  动圆问题解析时需要结合方法策略来转化问题条件、构建策略.常用的方法有特殊位置法、分类讨论法、化归转化法，本文结合实例探究解法，分析破题思路，并总结构建策略，与读者交流.

【关键词】  动圆；分类讨论；化动为静

动圆问题时是初中几何较为特殊的问题之一，问题常以圆的运动为背景来构建几何综合，探究学习时需要使用一定的方法技巧解析问题，降低思维难度.下面举例其中常用的三种方法：特殊位置法、分类讨论法、化归转化法.

1  把握特殊位置，构建模型推导

特殊位置分析是解析动圆问题的重要方法，通过分析动圆可到达的特殊位置来确定模型，解析时分两步构建：第一步，分析动圆的移动范围，结合问题确定其特殊位置；第二步，把握特殊位置构建模型，代入条件分析求解.

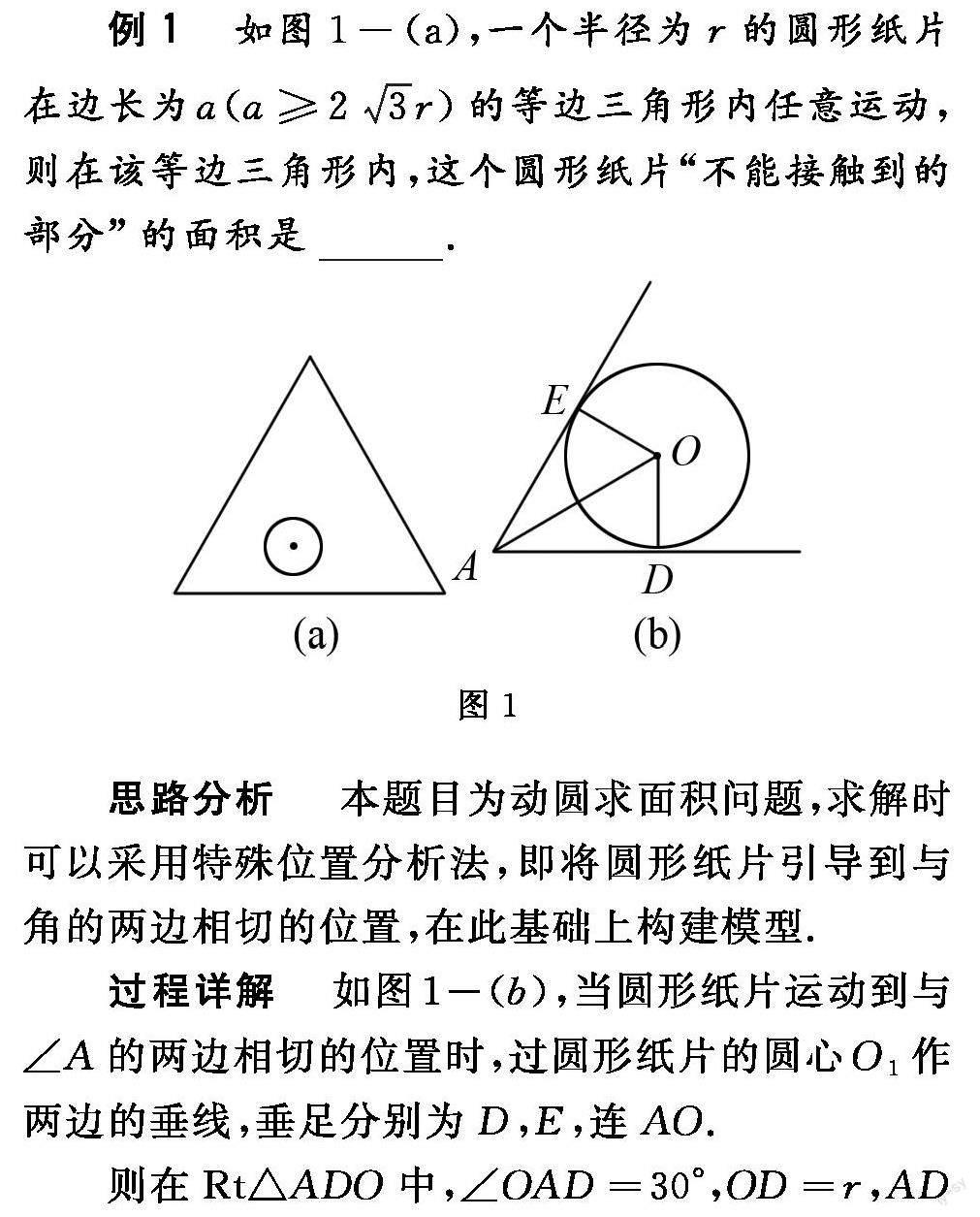
例1  如图1-（a），一个半径为r的圆形纸片在边长为a（）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是         .

思路分析  本题目为动圆求面积问题，求解时可以采用特殊位置分析法，即圆形纸片引导到与角的两边相切的位置，在此基础上构建模型.

过程详解  如图1-（b），当圆形纸片运动到与∠A的两边相切的位置时，过圆形纸片的圆心O1作两边的垂线，垂足分别为D，E，连AO1.

则在Rt△ADO1中，∠O1AD=30°，O1D=r，AD=，

可求得S△ADO1=，

S四邊形ADO1E＝2S△ADO=.

由题意可知，∠DO1E＝120°，

得S扇形O1DE=，

所以圆形纸片不能接触到的部分的面积为（-）=（）r2.

解后评析  上述求解求解动圆面积问题时，采用了特殊位置分析建模法，把握动圆与角相切时的特殊位置，构建面积模型分析.特殊位置分析时，需要关注两点：一是圆心的移动轨迹；二是圆与几何线段的相切关系.

2  合理分类讨论，分别简化分析

分类讨论在几何探究中十分常用，同样可以用于动圆综合题中.解析时需要分三步进行：第一步，解析动圆运动规律，确定分类标准；第二步，分情形进行模型讨论，推导求解；第三步，综合分析，确定最终结论.

例2  如图2所示，已知正方形ABCD的边长为8，点M是AB的中点，点P是BC边上的动点.连接PM，以点P为圆心，PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时，BP的长为         .

思路分析  本题目为动圆求线段问题，设定了圆心点P的移动轨迹，求解时需要讨论圆与正方形边相切的情形，在构建模型，提取其中直角三角形模型，解析求线段长.

过程详解  分两种情形讨论⊙P与正方形边相切，具体如下.

情形1  如图3-（a），当⊙P与直线CD相切时，设PC=PM=x，

在Rt△PBM中，由勾股定理可得PM2＝BM2+PB2，

代入线段长可得x2=42+（8﹣x）2，

可解得x＝5，

可推得PC=5，BP=BC﹣PC=3.

情形2  如图3-（b），当⊙P与直线AD相切时，

设切点为K，连接PK，则PK⊥AD，四边形PKDC是矩形.

可推知PM=PK=CD=2BM，

所以BM=4，PM=8.

在Rt△PBM中，由勾股定理可得PB=.

综上所述，BP的长为3或.

解后评析  上述动圆问题中，圆心的轨迹确定，求解线段长，需要讨论圆与线段的相切情形，故采用分类讨论的思维方法可极大降低思维难度.分类讨论求解动圆问题时，需要注意两点：一是慎重确定分类标准，不重复，不缺漏；二是对于每一种情形，要注意讨论是否成立.

3  几何化归转化，化动为静分析

化归转化同样可以用于动态几何问题中，求解时需要根据条件转化为一般的几何问题，如分析线段长、点位置坐标等.具体求解时需要挖掘动圆问题本质，根据条件进行转化，再结合模型讨论分析.

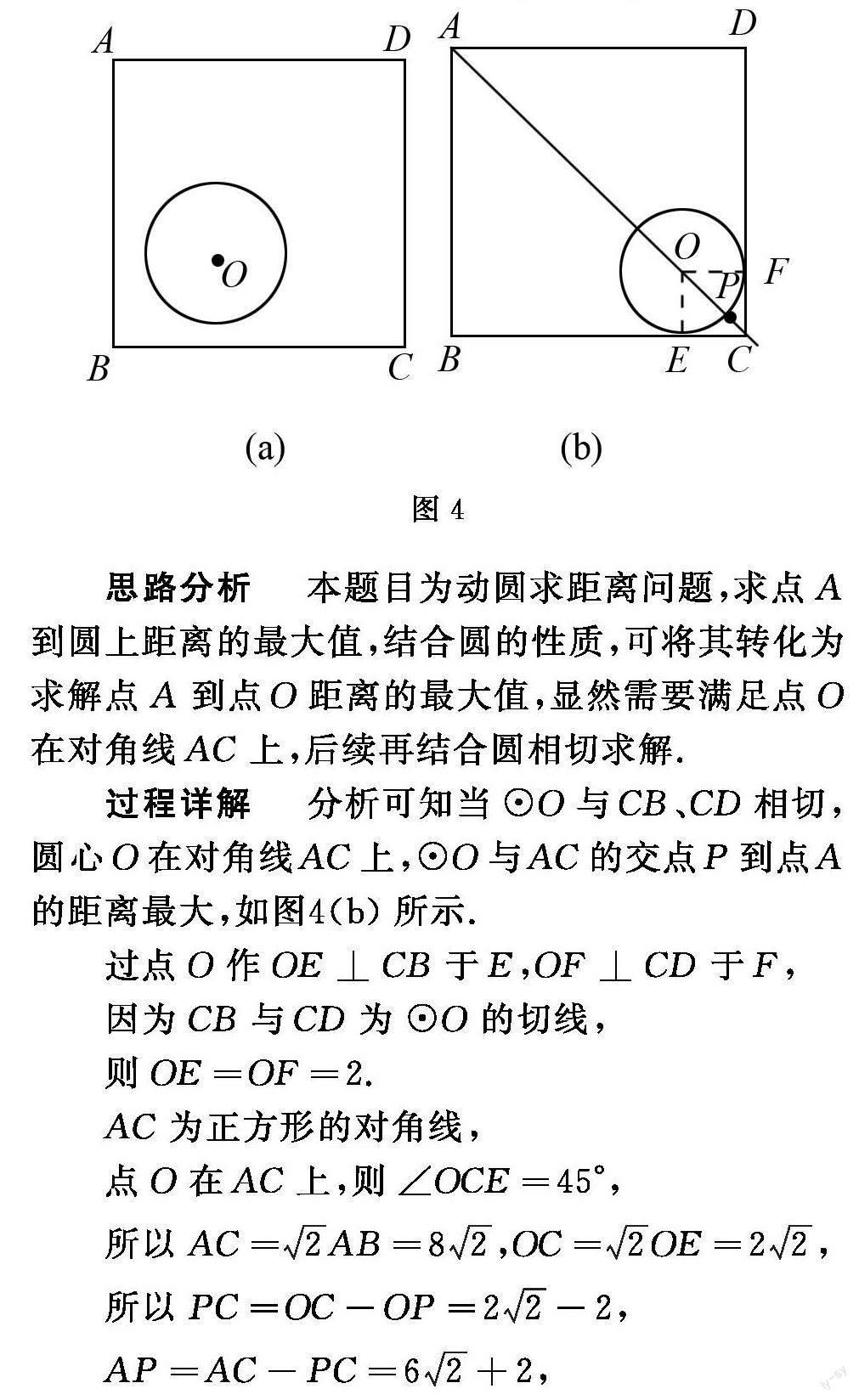
例3  如图4-（a）所示，已知正方形ABCD的边长为8，⊙O的半径为2.若⊙O在正方形ABCD内平移（⊙O可以与该正方形的边相切）.则点A到⊙O上的点的距离的最大值为         .

思路分析  本题目为动圆求距离问题，求点A到圆上距离的最大值，结合圆的性质，可将其转化为求解点A到点O距离的最大值，显然需要满足点O在对角线AC上，后续再结合圆相切求解.

过程详解  分析可知当⊙O与CB、CD相切时，圆心O在斜边AC上时，

⊙O与AC的交点P到A点的距离最大，如图4-（b），所示.

过O点作OE⊥CB于E，OF⊥CD于F，

因为CB与CD为⊙O的切线，

则OE=OF=2.AC为正方形的对角线，

O点在AC上，则∠OCE＝45°，

AC=，OC=，

所以PC=OC-OP=，

AP=AC﹣PC=，

即点A到⊙O上的点的距离的最大值为62.

解后评析  上述求解距离最值时，结合圆的性质将其转化为两点之间的距离，再结合共线性质求解.整体上采用的是“几何划归转化，化动为静”分析的思维方法.该方法再使用时分为两步：第一步，分析问题特征，挖掘问题本质，联系几何性质定理转化；第二步，分析转化后问题，再构建模型求解.

4  结语

总之，动圆问题的破解方法较为众多，上述所呈现是其中较为常见的三种，方法思路构建时均涉及到了数形结合、模型构造的思维方法.探究学习时，需要深刻理解方法本质，掌握方法精髓及构建策略.同时关注问题类型，结合问题总结方法策略.