爆炸冲击载荷作用下密加筋板塑性响应解析预报方法研究

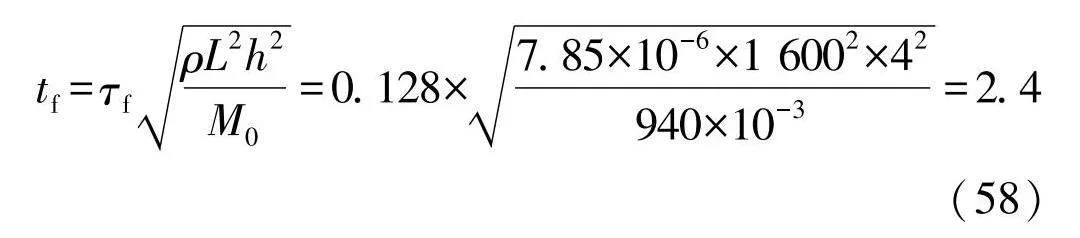
摘 要： 以钢质密加筋板为研究对象，研究了其在空气爆炸荷载作用下的爆炸响应.假设加筋板动力响应的变形模态与静力极限变形模态相同，采用能量原理和加筋板结构的塑性变形原理，分析得到了其在爆炸冲击载荷作用下塑性动力响应的运动控制方程.同时利用有限元软件ABAQUS对加筋板进行在空气爆炸荷载作用下的仿真分析，根据仿真分析结果对加筋板结构变形理论进行验证，为钢质加筋板的设计和抗冲击性能评估提供参考.

关键词： 密加筋板；冲击载荷；塑性变形；解析计算；数值仿真

中图分类号：U661.4"" 文献标志码：A"""" 文章编号：1673-4807（2024）06-022-10

收稿日期： 2023-07-27"" 修回日期： 2021-04-29

基金项目： 国家自然科学基金项目（52171311，52271279）

作者简介： 孟庆澳（1999—），男，硕士研究生，研究方向为船舶与海洋结构物性能.E-mail： 1921529952@qq.com

*通信作者： 刘昆（1984—），男，博士，教授，博导，研究方向为船舶与海洋工程结构强度分析评估及冲击动力学.E-mail： kunliu@just.edu.cn

引文格式： 孟庆澳，刘昆，纵帅，等.爆炸冲击载荷作用下密加筋板塑性响应解析预报方法研究［J］.江苏科技大学学报（自然科学版），2024，38（6）：22-31.DOI：10.20061/j.issn.1673-4807.2024.06.004.

Analytical prediction method for plastic response ofmulti-stiffened plates under the blast impact load

MENG Qingao， LIU Kun*， ZONG Shuai， WANG Zhengyao

（School of Naval Architecture and Ocean Engineering， Jiangsu University of Science and Technology， Zhenjiang 212100， China）

Abstract：In this paper， the explosion response of steel tightly reinforced plates under air explosion load is simulated. Assuming that the deformation mode of the dynamic response of the reinforced plate is the same as the static limit deformation mode， the energy principle and the plastic deformation principle of the reinforced plate structure are used to analyze and obtain the motion control equations of its plastic dynamic response under the action of the blast impact load. Meanwhile， the simulation analysis of the stiffened plate under the air blast load is carried out by using the finite element software ABAQUS， and the deformation theory of the reinforced plate structure is verified according to the simulation analysis results. A reference is provided for the design and impact resistance evaluation of steel stiffened plates.

Key words：multi-stiffened plate， impact load， plastic deformation， analytical calculation， numerical simulation

舰船结构主要采用加筋钢板建造，在演习和作战时易受到空气和水下爆炸的威胁，爆炸冲击波作用于舰船结构，会使结构产生损伤变形或破裂失效.因此，爆炸荷载下加筋板的设计是非常重要的.以往的工作主要集中在分析或数值变形预测和实验研究加筋板的塑性动力响应^［1-4］.虽然这方面的研究已经取得了很大的进展，但为了进一步理解加筋板在爆炸荷载作用下的动力响应机理，还需要进行理论分析，从而为加筋板的初步设计、安全研究和危害评估提供参考.文献［5-7］是第一个开发刚体、完美塑性方法来预测韧性梁和板永久位移的.通过画出准确的屈服曲线，将该方法简化为近似的屈服条件.文献［8-9］提出了爆炸荷载加筋板的简化刚塑性模型，文献［10］将该方法推广到预测水下爆炸作用下水下加筋板的非线性动力响应.计算结果与数值计算结果基本一致.文献［11-12］采用实验、理论和数值方法研究了受限爆炸荷载下加筋板的弹塑性动力响应.理论预测和数值模拟分别考虑了弹塑性效应和加劲筋位置的影响，结果与试验数据吻合较好.文献［13］采用能量原理分析了船底加筋板在水下爆炸冲击波荷载作用下塑性动力响应.文中以钢质密加筋板为研究对象，根据加强筋的相对刚度以及载荷峰值的大小分析加筋板在静力极限状态下的结构变形判别条件.在此基础上，以物体能量原理，结构的极限变形理论以及结构塑性力学等相关理论为依据，分析得到其在爆炸冲击载荷作用下的塑性动力响应的运动控制方程，并通过有限元仿真计算进行验证，验证完善理论预报方法的可靠性.

1 理论推导

1.1 变形模式的确定

1.1.1 理论分析模型

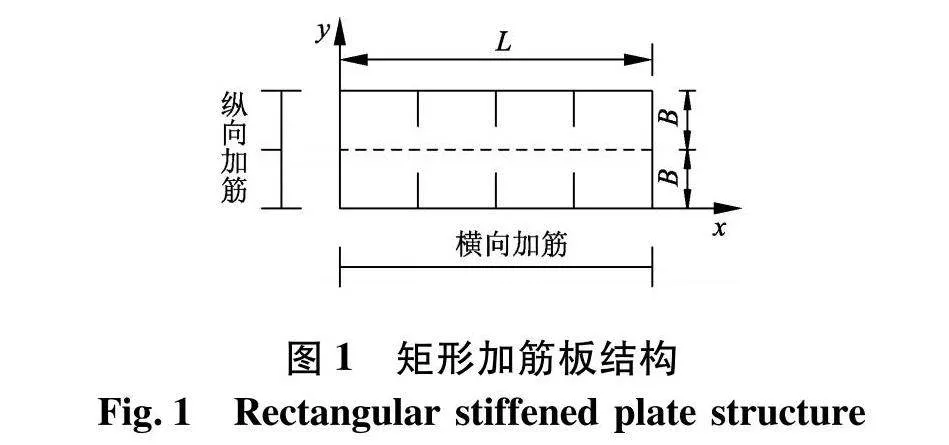
分析对象矩形加筋板，长度为L，宽度为2B，厚度为t，共有n根横向加筋和1根纵向加筋，如图1.

加筋板架中的加筋骨材与板格一起发生塑性变形.对于这类加筋板，由于横向次要构件（骨材）的数目较多，纵向强力构件（纵桁）较少，排列相对较密，为简化分析可作基本假设^［14］.

基本假设1：加筋板在板材与骨材刚度一定时，板材在变形过程中，同一点处加筋与板的变形相同，且加筋与板同时进入塑性状态，这样塑性铰线将连续通过板与加筋；

基本假设2：在同一刚性区域内，加筋板材在板材与骨材刚度一定时，加筋之间的板格的局部凹陷较小（忽略），加筋与板的变形是一致的.

基于上述假设，可将横向加筋按面积沿板面均摊，因为横向加筋在板长方向不能承受弯矩和轴力，从而整个加筋板简化为具有一根纵向加筋的正交异性板.

简化前，板的极限弯矩M0和膜力N0分别为：

M0=σyt24（1）

N0=σyt（2）

式中，σy为材料的屈服极限.

简化后，板在y方向的极限弯矩和x方向的极限膜力不变：

M0y=M0（3）

N0x=N0（4）

简化后，板在x方向的极限弯矩和y方向的极限膜力分别为：

M0x=σyt2e4（5）

N0y=σyte（6）

正交异性板在方向上的相当板厚为：

te=t+nA1L（7）

式中，A1为单根横向加筋截面积.

1.1.2 静力极限分析

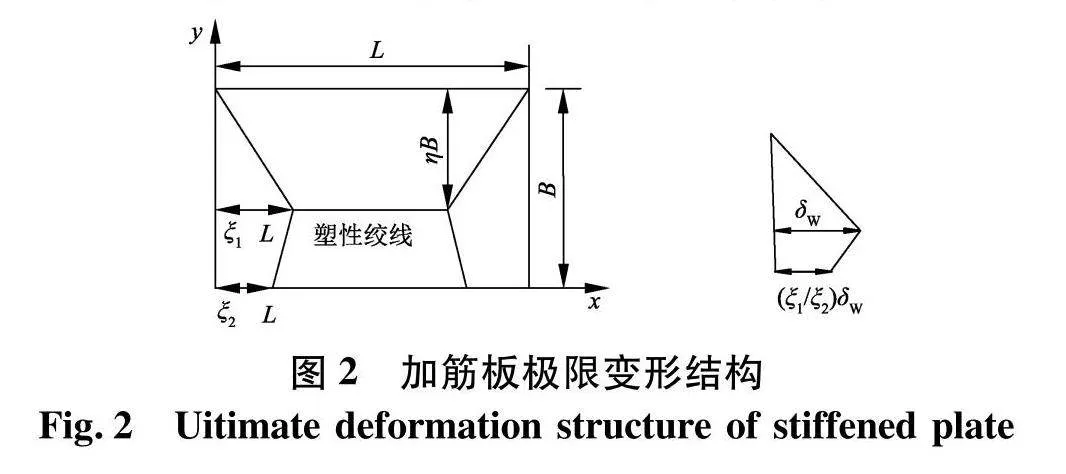
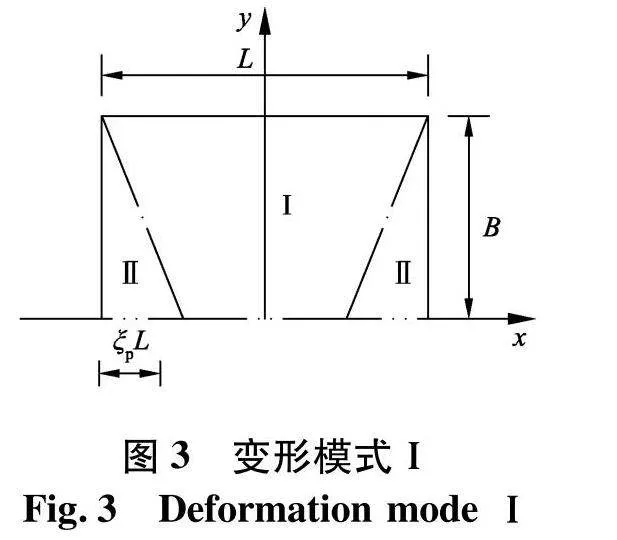
考虑到结构对称、载荷对称引起的变形也是对称的，故可取1/2加筋板进行分析，其变形模式可通过静力极限分析方法确定.根据分析各类板结构的经验，假设加筋板处于极限状态时，其塑性铰线的分布如图2，ξ1、ξ2和η为确定塑性铰线位置的无因次参数^［15-18］，δw为板上的最大横向变形.

这种假设机构是最一般的形式，可由其得到纵向加筋仅有1个塑性铰（ξ2=0.5），或不发生塑性变形（ξ2=0）的情况.

设为均布横向外载荷，可求得外力总虚功为：

W=qLBδw（3ξ1－2ξ21+（1－η）（3ξ2－2ξ1ξ2－2ξ22）6ξ1）（8）

若边界固定程度是任意的，以参数ε表示，则

（1） 当边界完全固定时，ε=1

（2） 当边界为简支时，ε=0

内力总虚功的表达式：

U=M0δwξ1LB×（1+ε）（k1ξ1L2+2B2+k2LB）""""" η=1

M0δwξ1η（1－η）LB×（（1+ε）（1－η）+2η）k1ξ1L2+2η（1+ε）（1－η）B2ξ2=0

M0δwξ1η（1－η）LB×k1L2（1+ε）（1－η）+2η（1－2ξ2）（ξ1－ξ2）ξ1k1L+η（1+ε）（1－η）（2B2+k2LB）ξ2gt;0，ηlt;1（9）

式中：k1=M0xM0，k2=MbM0L .

Mb为纵向加筋的极限弯矩，令：

β=BLλ1=k1β2λ2=2+k2β（10）

λ1、λ2实际上表征了横向加筋和纵向加筋各自的刚度特征.

由W=U可得载荷为：

（1） η=1时

q=6M0βLB·（1+ε）（λ1ξ1+λ2）3ξ1－2ξ21（11）

（2） ξ2=0时

q=6M0β（（1+ε）（1－η）+2η）ξ1λ1+2η（1+ε）（1－η）ηLB（1－η）（3ξ1－2ξ21）（12）

（2） ξ2gt;0，ηlt;1时

q=6M0β（ξ1（1+ε）（1－η）+2η（1－2ξ2）（ξ1－ξ2））λ1LBη（1－η）（3ξ1－2ξ21+（1－η）（3ξ2－2ξ1ξ2－2ξ22））+

6M0βη（1+ε）（1－η）λ2LBη（1－η）（3ξ1－2ξ21+（1－η）（3ξ2－2ξ1ξ2－2ξ22））（13）

根据极限分析原理，极限状态时的实际变形模式应使极限外载荷做功最少，即对应的外载荷应取极小值.

分3种情况讨论：

（1） η=1时，ξ1=ξ2

由qξ1=0可得极限状态时板架的铰线位置：

ξp=λ22+32λ1λ2－λ2λ1（14）

对应的极限载荷为：

qc=6M0λ1β（1+ε）（3－4ξp）LB（15）

此模式下显然应有ξp≤12，从而可得：

λ2λ1≤12（16）

（2） ξ2gt;0，ηlt;1时

由qξ1=0qξ2=0qη=0 且0≤ξ1≤120≤ξ2≤12

可得ξ1=ξ2=12时的铰线位置：

ηp=λ21+6λ1λ2－λ12λ2（17）

对应的极限载荷为：

qc=6M0λ1β（1+ε）η2pLB（18）

由ηp≤1得到这一模式的条件为：

λ2λ1≥12（19）

（3） ξ2=0时

这种情况对应纵向加筋不发生塑性变形，只有在λ2很大时才出现.

由qη=0可得：

ηp=2（1+ε）－（1+ε）1－ε（20）

由上式可知，ηp仅与边界的固定程度有关.

当ε=0时ηp=2－1

当ε=1时，limε→1 ηp=12；

由qξ1=0，代入ηp，令：

ε1=（1+ε）（3+ε－22（1+ε））（1－ε）2（21）

当ε=0时，ε1=3－22，当ε=1时，limε→1 ε1=14

得塑性铰线：

ξp=4ε21+3ε1λ1－2ε1λ1（22）

对应的极限载荷为：

qc=6M0λ1β（1+ε）（3－4ξp）ε1LB（23）

按照极小载荷条件，出现这一变形模式时，式（3）中求得的载荷应比式（2）中求得的载荷要小，可求得不等式的解为：

λ2λ1gt;λ （24）

其中：

λ =（4ε1+3λ1－2ε1λ1+2ε1）（4ε1+3λ1+2ε1）6ε1λ1（25）

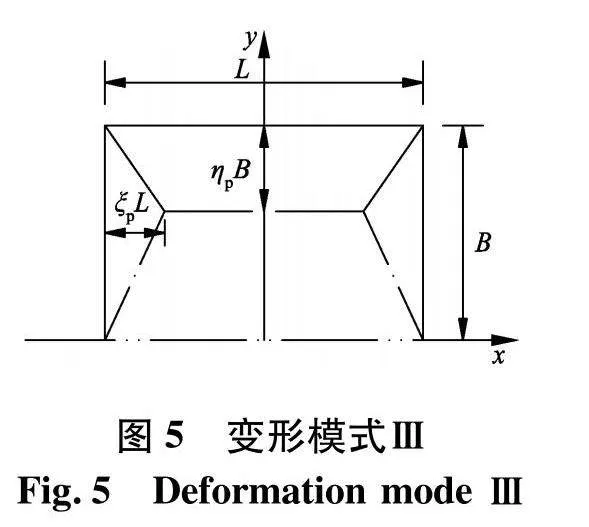
综上分析可知，根据不同的纵、横向加筋刚度比，加筋板在静力极限状态时，将有3种可能发生的变形模式Ⅰ，Ⅱ，Ⅲ，3种模式对应的极限载荷为：

（1） 如果λ2λ1≤12，为变形模式Ⅰ：

ξp=λ22+32λ1λ2－λ2λ1

极限载荷为：qc=6M0λ1β（1+ε）（3－4ξp）LB

（2） 如果12≤λ2λ1≤λ ，为变形模式Ⅱ：

ηp=λ21+6λ1λ2－λ12λ2

极限载荷为：qc=6M0λ1β（1+ε）η2pLB

（3） 如果ξ2=0，为变形模式Ⅲ：

ηp=2（1+ε）－（1+ε）1－ε，ξp=4ε21+3ε1λ1－2ε1λ1

极限载荷为：qc=6M0λ1β（1+ε）（3－4ξp）ε1LB

1.2 塑性动力响应分析

在结构的塑性动力响应过程中，结构上的塑性铰会发生移动.由于动力响应的最终残余变形模式往往与静力极限变形模式相接近，且塑性铰移动所耗散的能量比重不大，故可假设结构以静力极限状态时的变形模式响应，且在整个动力响应过程中不变^［19-20］.

屈服准则采用Johansen外接方形屈服条件，即屈服时：

MM0=±1 NN0=±1（26）

式中，M0、N0为板在某一方向上的极限弯矩和膜力或纵向加筋的极限弯矩和轴力.

1.2.1 运动方程

将Jones-Sawczuk控制方程应用于加筋板，由外力总虚功率等于内力总虚功率，得：

∫A（q－ρ1w¨）w·dA+∫l（－ρ2w¨）w·dl=

∑m1i=1∫li（Nw－M）θ·idli+∑m2j=1（Nrw－Mr）θ·j（27）

式中：M、N为板的弯矩和膜力；Mr、Nr为纵向加筋的弯矩和轴力；ρ1为板的单位面积质量；ρ2为纵向加筋单位长度的质量；A为板的面积；li为第i根铰线长度；w、w·、w¨分别为纹线的横向位移、横向速度、横向加速度；θ·i为板上第i根铰线处的相对角速率；θ·j为加筋上第j个塑性铰处的相对角速率；m1为板上铰线数；m2为纵向加筋上塑性铰的数目.

以第Ⅰ种变形模式为例：

设w0（t）为任意t时刻板上最大横向变形，则变形场可表示为

刚性区域Ⅰ：

w（x，y，t）=w0（t）""" 0≤x≤L2－ξpL

（1－yB）w0（t）L2－ξpL≤x≤L2（28）

刚性区域Ⅱ：

w（x，y，t）=1－2xL2ξpw0（t）（29）

将w表达式及屈服条件代入控制方程，并定义无因次参数：

τ=tM0ρL2h2p（τ）=q（τ）L2M0（30）

则对应于第Ⅰ种变形模式时的运动方程：

（1－ξp）μ13+（3－4ξp）μ26βu¨+4（1－ξp）R1β2+β+R2ξpβu=

3－2ξp6p（τ）－（1+ε）λ1+λ2ξp（31）

式中：R1=N0yN0R2=NbN0Lμ1=ρ1ρhμ2=ρ2ρhL .

同理，对应于另外两种变形模式时的运动方程分别为：

1－ηp2μ13+μ26βu¨+4R12ηpβ2－2ηp+4β－2R2βu=3－ηp6p（τ）－（1+ε）λ1ηp+2λ2 （32）

（1－ξp）μ13u¨+4（1－ξp）R1ηp（1－ηp）β2+1ξpu=

3－2ξp6p（τ）－（1+ε）λ1ε1+2ξp（33）

可将3种变形模式时的运动方程统一表示为二阶常微分方程：

D1u¨+D2u=D3p（τ）－D4（34）

1.2.2 塑性变形

爆炸载荷^［21］可由指数形式为：

p（τ）=pm1－ττde^－α0ττd" 0≤τ≤τd

0τgt;τd（35）

式中：pm为载荷峰值；τd为作用时间；α0为衰减系数（α0=0时即为三角形载荷）.

根据爆炸载荷的特点，将变形模式所对应的运动方程，即二阶常微分方程，分为两个阶段求解.

（1） 第一阶段（0≤τ≤τd）

由初始条件：u（0）=0，u·（0）=0

求得任意时刻的变形：

u1（τ）=α1cos（ωτ）+α2sin（ωτ）+（α3+α4τ）e^－α0ττd－D4D2（36）

式中：ω=D2D1；α1=D4D2－α3；α2=α0α3τd－α4ω；

α3=－α4τd（1+2D1α0α4D3pmτd）；α4=－D3pmτdD1α20+D2τ2d .

若载荷峰值不大或持续时间较长，则响应有可能在第一阶段结束，其时间τf=τs可根据u·1（τs）=0求得，最大残余变形可将τs代入式（32）中计算得出.

若求出τsgt;τd，则当τgt;τd时，响应进入第二阶段，由式（32）可求得第一阶段结束时板上最大变形u1（τd）及该处速度u·1（τd）.

（2） 第二阶段（τgt;τd）

此阶段无外载荷，初始条件为：

u（τd）=u1（τd）u·（τd）=u·1（τd）（37）

运动终止时间为：

τf=τd+arctanβ2β1ω（38）

式中：β1=u1（τd）+D4D2；β2=u·1（τd）ω.

最大塑性变形为：

umax=u（τf）=β1cos ω（τf－τd）+β2sin ω（τf－τd）－D4D2（39）

1.3 算例分析

1.3.1 计算模型

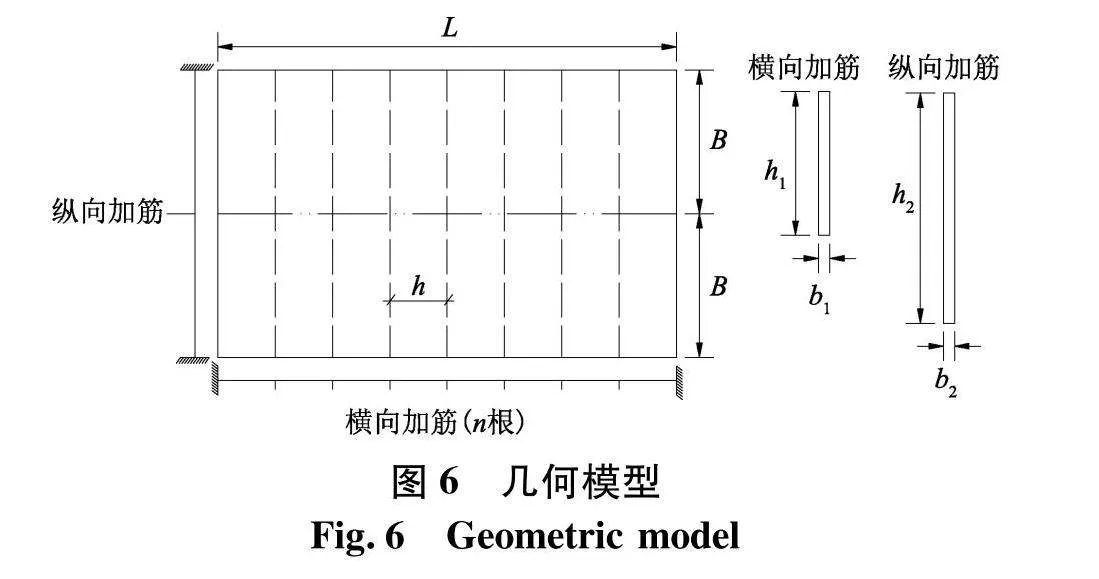
基于上述能量法理论，以某一类具有一根纵向加筋及若干横向加筋的加筋板结构为研究对象，开展爆炸载荷作用下的结构动态响应计算，所分析结构的几何模型如图6.

将上述具有一根纵向加筋及若干横向加筋的加筋板的边界取为固支，即板和横向加筋的尺寸相同，而纵向加筋则根据可能不同的变形模式取3组不同的尺寸，见表1.

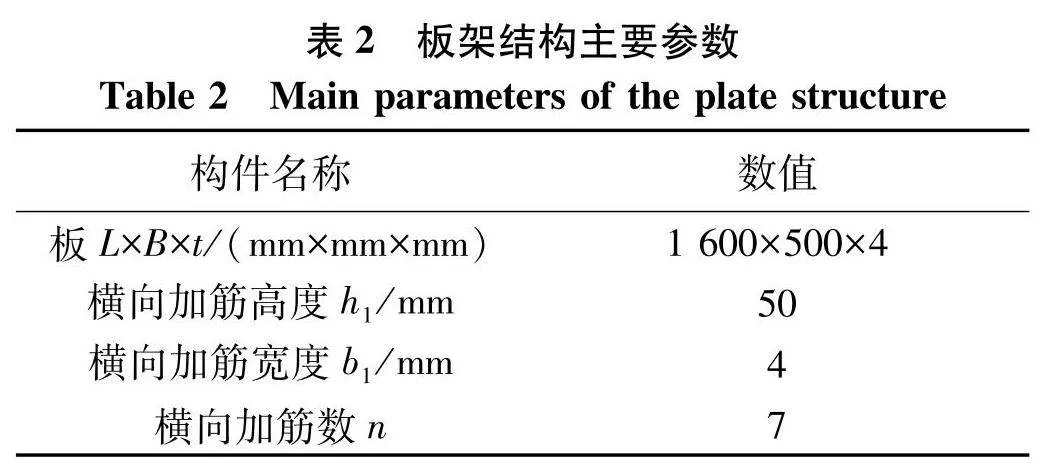
（1） 板架结构的主要参数如表2.

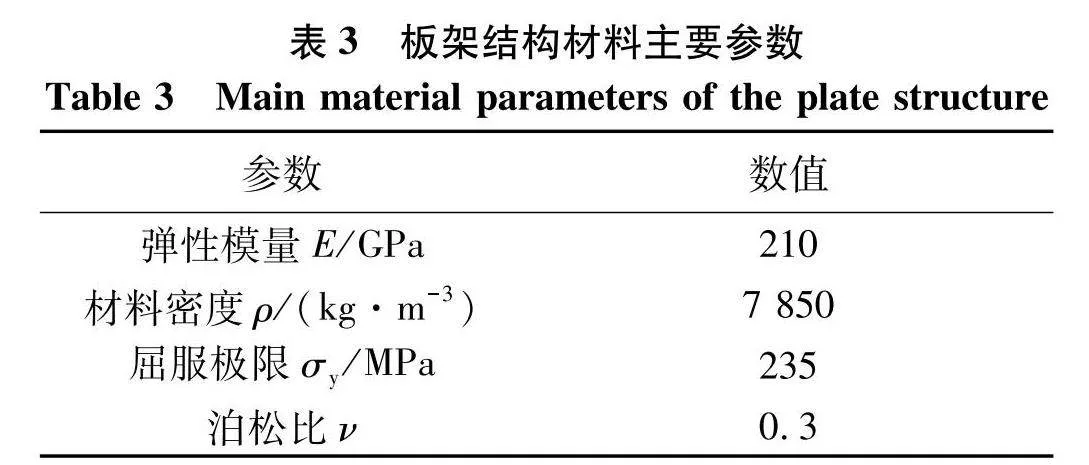
（2） 材料本构关系假定为弹性-理想塑性，主要性能参数如表3.

基于静力极限理论，假设动力响应的变形模式与静力极限状态时的变形模式一致，根据材料的刚塑性本构关系，可采用能量法推导出结构的变形机构模式以及该种变形模式的判别条件.以图6中的实际加筋板架为例，通过计算判定不同板架模型的变形模式，即四边固支且具有相同尺寸的板和横向加筋、不同尺寸的纵向加筋的板架的静力极限变形模式，同时为后续基于Jones-Sawczuk控制方程分析爆炸载荷作用下加筋板塑性动态响应提供相应参数.

1.3.2 变形模式的确定

基于基本假设，将横向加筋按面积沿板面均摊，可得简化后的加筋板的相当板厚为：

he=h+nA1L=4+7×（50×4）1 600=4.875（40）

假定材料本构关系为弹性-理想塑性，根据材料的屈服极限σy=235 MPa，可得简化前板的极限弯矩为：

M0=σyh24=235×424=940（41）

而简化后板在x方向的极限弯矩为：

M0x=σyh2e4=235×4.87524=1 396.23（42）

纵向加筋的极限弯矩为：Mb=σyb2h224，可知对于不同尺寸的纵向加筋，其极限弯矩不相同，现以表1中第1种纵向加筋为例，计算其极限弯矩，从而得到简化后加筋板架的纵向刚度特征，以此判定板架的变形模式.即当纵向加筋的高h2=80 mm，宽度b2=4 mm，其极限弯矩为：

Mb=σyb2h224=235×4×8024=1 504 000（43）

因此，内力总虚功U表达式（9）中的系数k1、k2分别为：

k1=M0xM0=1 396.23940=1.485 4（44）

k2=MbM0L=1 504 000940×1 600=1（45）

板的形状系数为：

β=BL=5001 600=0.312 5（46）

从而表征横向加筋和纵向加筋各自刚度特征的参数λ1、λ2分别为：

λ1=k1β2=1.485 40.312 52=15.21（47）

λ2=2+k2β=2+10.312 5=5.2（48）

所以，λ2λ1=5.215.21=0.34.

同理可得：

表1中第2种纵向加筋的加筋板：λ1=15.21，λ2=18.2，λ2λ1=1.20；

表1中第3种纵向加筋的加筋板：λ1=15.21，λ2=92，λ2λ1=6.05.

由3组λ1、λ2的值可知，因为3种板架具有相同数量及尺寸的横向加筋，因此3种板架的λ1值相同，即板架的横向刚度特征相同；而3种板架纵向加筋不同，且随着纵向加筋的尺寸增大，λ2值也相应地增大，表征板架的纵向刚度特征与纵向加筋有关，且纵向加筋的尺寸越大，板架的纵向刚度越大.而板架的纵横向刚度特征决定了板架的变形模式，因此λ2/λ1值的大小可作为判定板架变形模式的参数.

根据加筋板四边固支，即ε=1，此时ε1=14，则式（25）可化简为：

λ =2（1+3λ1－λ1+1）（1+3λ1+1）3λ1（49）

可见此时λ 值仅与的λ1值有关，由于上述3种板架的λ1值相同，因此3种板架的λ 值均为：

λ =

2（1+3×15.21－15.21+1）（1+3×15.21+1）3×15.21=1.35（50）

由分析可知：

对于表1中第1种板架，因为λ2λ1≤12，为变形模式Ⅰ；

对于表1中第2种板架，因为12≤λ2λ1≤λ ，为变形模式Ⅱ；

对于表1中第3种板架，因为λ2λ1gt;λ ，为变形模式Ⅲ.

1.3.3 塑性动力响应分析

根据爆炸载荷作用下加筋板的塑性动力响应分析，首先通过将加筋板具体变形模式下的变形场和屈服准则代入Jones-Sawczuk控制方程，可得到该变形模式下的运动方程.接着将以指数方程形式表示的爆炸载荷代入上述运动方程，其中爆炸载荷的表示参数载荷峰值和作用时间均进行了相应的无量纲化，此时运动方程即转化为一个二阶常微分方程，求解该二阶常微分方程，即可得加筋板架在任意时刻的变形表达式.若爆炸载荷峰值不大或爆炸持续时间较长，则可通过对上述变形表达式求一阶导数的零点，即为产生最大变形所对应的时间，从而求得最大塑性变形；若求出的零点值大于爆炸的作用时间，则将爆炸结束时板架所对应的状态作为下一运动阶段的初始条件，再次通过表达式解出最大塑性变形.

根据上述理论，可知3种变形模式求解最大塑性变形的过程基本相同，仅是运动方程及方程解的表达式中各参数有所差异，前文已经确定3种板架的变形模式，通过确定加筋板的绞线位置，可得出式（32）中的各参数ξp、β、μ1、μ2、R1、R2、ε、λ1、λ2数值，代入式（32），则二阶常微分方程式（32）中个项前的系数分别为D1=0.215、D2=37.647、D3=0.349、D4=53.446.

式（35）通过函数关系表示了爆炸载荷的冲击压力随时间变化的过程，其中重要的表征参数为峰值压力、持续时间及衰减系数这3项.为简化解析计算，可令衰减系数α0=0，此时指数形式的爆炸载荷则转化为三角形载荷，即初始时刻为峰值压力且压力随时间线性衰减直至为零的载荷-时间关系.式（35）可简化为：

p（τ）=pm1－ττd" 0≤τ≤τd

0τgt;τd（51）

由于对应于变形模式的运动方程均进行了无量纲化处理，因此上述爆炸载荷的表征参数也需要进行无量纲化.

此时假定给假设加筋板架施加一峰值压力qm=0.8 MPa、持续时间td=1.2 ms的三角形载荷，则对qm、td进行无量纲化：

pm=qmL2M0=0.8×1 6002940=2 178.72

τd=tdM0ρL2h2=1.2×940×10^-37.85×10^-6×1 6002×42=

0.064 9（52）

此时运动方程的解的表达式（36）中的相关系数所涉及的参数α0、D1、D2、D3、D4、pm、τd均已知，则此时运动方程解的表达式（36）可表示为：

u1（τ）=－18.8cos （13.24τ）+23.53sin （13.24τ）-

311.69τ+18.8（53）

对上述方程求一阶导数，即为：

u·1（τ）=248.91sin （13.24τ）+

311.69cos （13.24τ）－311.69（54）

则：u1（τd）=4.13，u·1（τd）=80.46

从而可得：

β1=u1（τd）+D4D2=4.13+53.44637.647=5.55（55）

β2=u·1（τd）ω=80.4613.24=6.07（56）

所以产生最大变形的时间τf为0.128，代入式（39）可得时间所对应的最大塑性变形为6.81.

所求解的τf、umax均为无量纲的，则实际值为：

w0=umaxh=6.81×4=27.2（57）

tf=τfρL2h2M0=0.128×7.85×10^-6×1 6002×42940×10^-3=2.4（58）

同理，对于表1中的第2种板架，由上节分析已知其为变形模式Ⅱ，对其施加一个峰值压力为1.0 MPa、持续时间为1.2 ms的三角形爆炸冲击载荷，通过对其运动方程的求解，可得最大塑性变形w0=27.3 mm，产生最大变形的时间tf=2.3 mm；对于表1中的第3种板架，由上节分析已知其为变形模式Ⅲ，对其施加一个峰值压力为1.2 MPa、持续时间为1.2 ms的三角形爆炸冲击载荷，通过对其运动方程的求解，可得最大塑性变形w0=19.7 mm，产生最大变形的时间tf=1.4 ms.

2 数值仿真分析

以表1中的3种加筋板架为研究对象，利用非线性有限元分析软件ABAQUS进行数值仿真计算，得到加筋板架在爆炸载荷作用下的动力响应，以此分析影响加筋板架动力响应的因素及加筋板架的响应规律，并将结果与上节中基于能量法的理论解进行比较，从而验证理论解的可靠性.

2.1 有限元模型

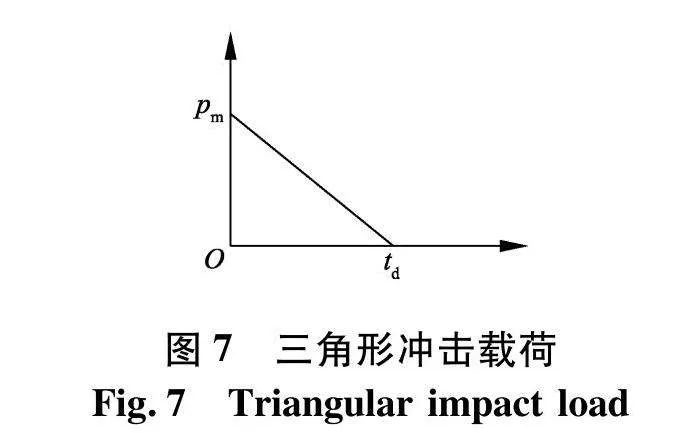
运用ABAQUS所建的加筋板架的几何尺寸及材料属性与算例中给出的相同，应用显式动态方法求解.根据前述计算，可知加筋板架的约束条件为四边固支，因此在有限元分析模型中采用相同约束.爆炸载荷可简化为三角形冲击载荷，如图7.

其中：Pm为载荷峰值压力；td为载荷持续时间.

对应于表1中的3种纵向加筋，即3种不同几何模型的加筋板架，所施加的载荷形式如表4.

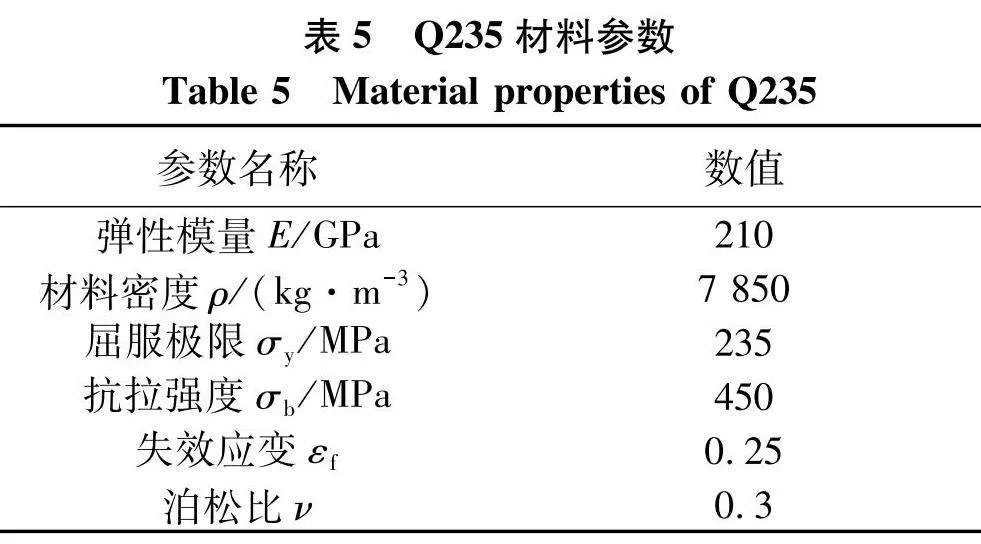
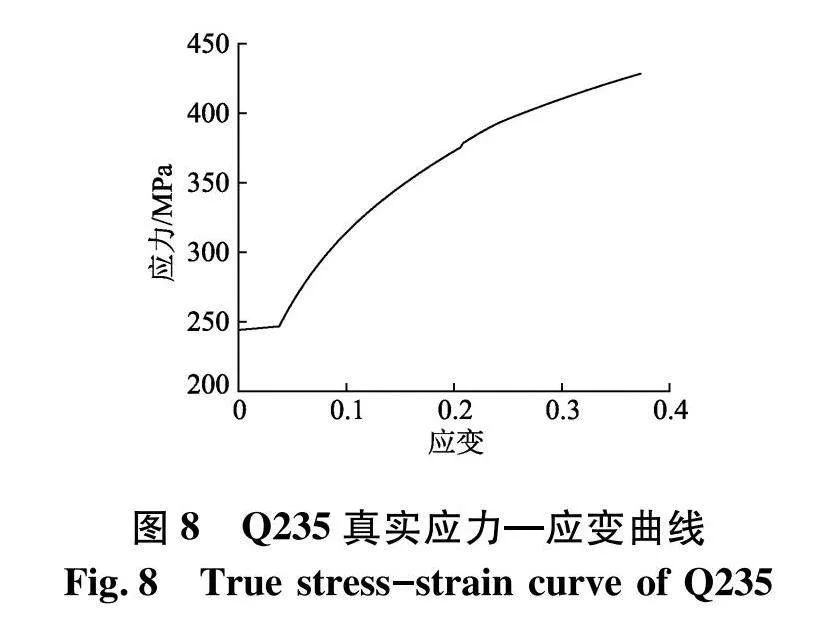
仿真材料选用Q235材料，与前文理论分析中参数一致，其真实应力—应变曲线如图8，参数值如表5.

有限元模型网格特征长度选取5 mm，网格划分如图9.

2.2 计算结果分析

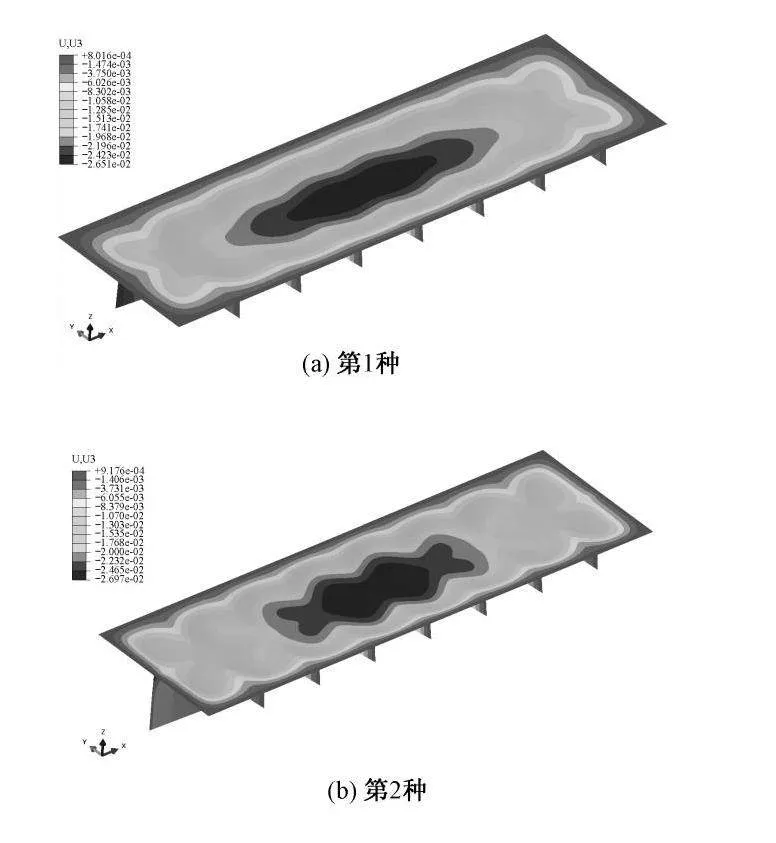
通过有限元模型的计算，可分别获得3种不同的加筋板架在相应的爆炸载荷作用下的动力响应，其在横向上的变形云图如图10.

通过云图可知，尽管3种加筋板架的面板和横向加筋相同，但由于纵向加筋的尺寸有所区别，从而3种板架的刚度特征不同，由静力极限分析理论可知，刚度的不同将导致板架的变形模式不同.3个云图分别对应了理论解析中的变形模式Ⅰ、Ⅱ、Ⅲ，即由于纵向加筋相对刚度的不同，使得加筋板架上产生的塑性铰线的位置不相同，且云图中显示的塑性平台区形状与理论解析中的塑性平台区的形状大致相同，从而表明基于能量法判别加筋板架变形模式的方法的可行性.

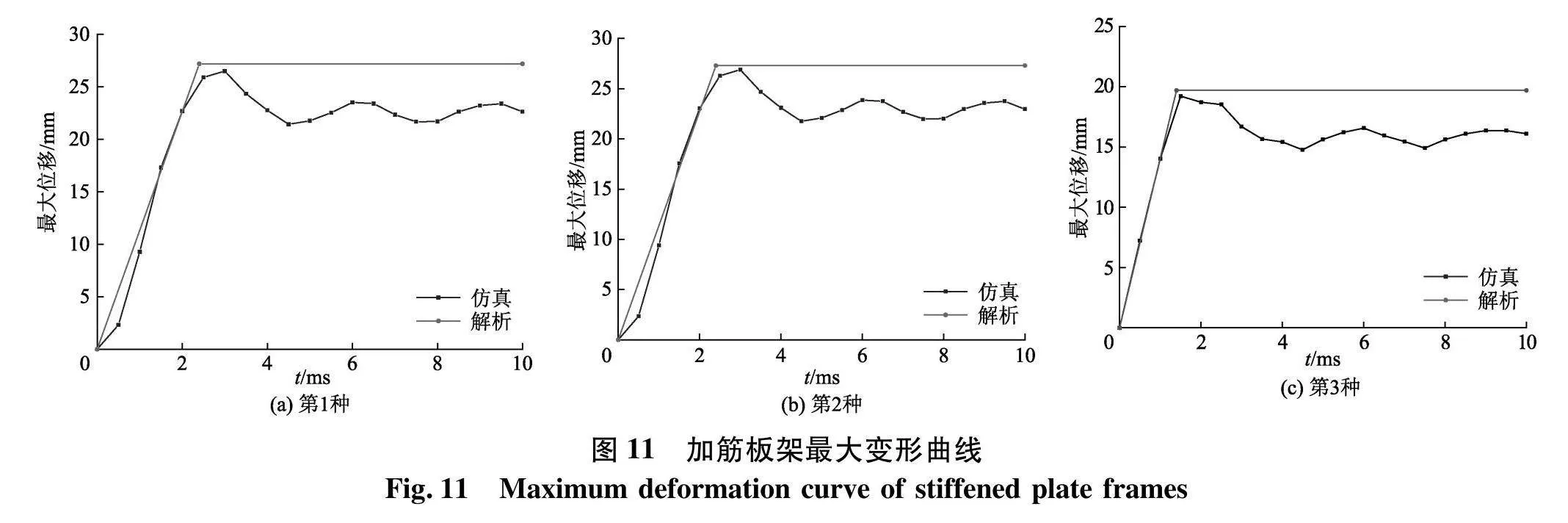
通过绘制变形云图中产生最大变形点的变形-时间曲线，并将其与理论解进行比较分析，如图11及表7.

通过表7可知，仿真变形与解析变形存在相对误差，而仿真变形相对于解析变形要小，其原因是理论解和仿真解相比结果偏大，这是由于在理论分析时对模型进行了简化，产生了偏大的解析数值.理论结果并没有考虑爆炸载荷下结构的材料的硬化及应变率影响，具有一定的保守性，适用于设计初期结构强度评估.

通过仿真计算的最大变形曲线可知，板架在承受爆炸载荷作用时，其变形迅速增大，但爆炸载荷结束后，由于爆炸载荷峰值压力大且持续时间短的特性，因此加筋板架仍然具有相当大的加速度，从而板架会进一步发生变形，板架变形达到最大之后，板架将进入自由振动阶段，这与变形曲线图上的波动阶段相吻合.

结合最大变形曲线及表可知，解析结果相对保守，从而更加偏于安全，且到达最大变形所需的时间，解析结果与仿真结果较为接近，故可其对结构在爆炸载荷作用下结构失效的预报具有指导意义.

3 结论

（1） 研究了加筋板在静力极限状态下的结构变形判别条件，运用能量法推导了加筋板在爆炸冲击载荷作用下的塑性动力响应的运动控制方程.

（2） 运用理论公式分别计算了3种不同尺寸加筋板的塑性变形，并将结果与有限元计算结果进行比较，验证了理论解的可靠性.

（3） 能量法能够快速分析评估结构在爆炸载荷下的响应，但其主要针对板、梁及加筋板架结构，且需做一定的简化处理，具有一定的局限性.

（4） 基于能量法推导的理论公式，其预报结果相比有限元仿真略微保守，从而更加偏于安全，可以有效预报爆炸载荷作用下结构相应.

参考文献（References）

［1］ RUDRAPATNA N S， VAZIRI R， OLSON M D. Deformation and failure of blast-loads stiffened plates［J］. International Journal of Impact Engineering， 2000， 24（4）： 457-474.

［2］ 侯海量， 朱锡， 古美邦. 爆炸荷载作用下加筋板的失效模式分析及结构优化［J］. 爆炸与冲击， 2007， （1）：26-33.

［3］ 牟金磊， 朱锡， 张振华， 等.水下爆炸载荷作用下加筋板变形及开裂试验研究［J］. 振动与冲击， 2008， 27（1） ： 57-60．

［4］ 张振华， 陈平毅， 漆万鹏， 等. 舰船局部板架结构在水下爆炸冲击波下动态响应的相似律研究［J］. 振动与冲击， 2008， 27（6）： 81－86．

［5］ JONES N. A theoretical study of the dynamic plastic behavior of beams and plates with finite-deflections［J］. International Journal of Solids and Structures， 1971， 7（8）： 1007-1029.

［6］ JONES N. Impact loading of ductile rectangular plates［J］. Thin-Walled Structures， 2012， 50： 68-75.

［7］ JONES N. Dynamic inelastic response of strain rate sensitive ductile plates due to large impact， dynamic pressure and explosive loadings［J］. International Journal of Solids and Structures， 2014， 74： 3-15.

［8］ SCHUBAK R B， OLSON M D， ANDERSON D L. Rigid-plastic modelling of blast-loaded stiffened plates-Part I： One-way stiffened plates［J］. International Journal of Mechanical Sciences， 1993， 35（3/4）： 289-306.

［9］ OLSON M D. Efficient modelling of blast loaded stiffened plate and cylindrical shell structures［J］. Computers amp; Structures， 1991， 40（5）： 1139-1149.

［10］ JIANG J， OLSON M D. Rigid-plastic analysis of underwater blast loaded stiffened plates［J］. International Journal of Mechanical Sciences， 1995， 37（8）： 843-859.

［11］ ZHENG C， KONG X， WU W， et al. The elastic-plastic dynamic response of stiffened plates under confined blast load［J］. International Journal of Impact Engineering， 2016， 95： 141-153.

［12］ ZHENG C， KONG X S， WU W， et al. Experimental and numerical studies on the dynamic response of steel plates subjected to confined blast loading［J］. International Journal of Impact Engineering，2018，113：144-160.

［13］ 方斌， 朱锡， 张振华. 水下爆炸冲击波荷载作用下船底板架的塑性动力响应［J］． 哈尔滨工程大学学报， 2008， 29（4）： 326-331．

［14］ 刘昆，张延昌，王璞，等.半潜式钻井平台撑杆结构极限承载力数值仿真计算［J］.江苏科技大学学报（自然科学版），2012，26（5）：430-433.

［15］ 杨平. 船体结构极限强度及破损剩余强度的研究［D］. 武汉：武汉理工大学，2005.

［16］ 温保华， 洪伟， 吴嘉蒙. 浅谈极限强度在船舶结构设计的运用［J］. 上海造船， 2007（3）： 8-10.

［17］ PAIK J K ，THAYAMBALLI A K .Ultimate limit state design of steel-plated structures［J］.Journal of Comparative Neurology， 2003， 388（3）：397-414.

［18］ MUNCER P B M .Analysis of accident statistics for floating monohull and fixed installations［R］. UK：Health and Safety Executive， 2003.

［19］ ELLINAS C P ， KWOK R ， WILLIAMS K A J .Collision damage of jack-ups［J］.Marine Structures， 1989， 2（3/4/5）：265-279.

［20］ MOAN T ， AMDAHL J ， WANG X ，et al.Risk assessment of FPSOs with emphasis on collision［J］.Transactions， 2002， 110：307-339.

［21］ ALI R M M. Performance based design of offshore structures subjected to blast loading［D］. London： Imperial College London， 2008.

（责任编辑：贡洪殿）