用转化法推导面积公式

刘北荣

转化是一种重要的数学思想。在学习数学时，我们经常会遇到新的问题，这时我们可应用转化，将陌生的新知转化成熟悉的旧知。例如，在学习三角形面积计算公式的推导时，我们就可以把三角形转化成已学过的平行四边形。

1.把两个同样的三角形拼成一个平行四边形。

通过观察发现：拼成的平行四边形的底相当于三角形的底，高相当于三角形的高，每个三角形的面积是平行四边形的面积的一半。平行四边形的面积=底×高，所以，三角形的面积=底×高÷2。

2.把一个三角形剪拼成平行四边形。

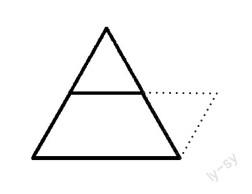
把三角形的中点（两腰）用线连接起来。顺着这条线剪开，把上面的三角形旋转（或拼、补），这样就成了一个平行四边形。这里，平行四边形的面积与三角形的面积相等。平行四边形的底与三角形的底相同，平行四边形的高是三角形的高的一半。因此，三角形的面积=平行四边形的面积=底×高÷2。

又如，推导“梯形面积”计算公式时，根据已有的知识（平行四边形、三角形面积公式推导方法）推导出梯形面积计算公式。

1.把两个完全一样的梯形拼成一个平行四边形（如图1）。

通过观察所拼的图形可知：梯形的上底加下底就是拼成的平行四边形的底，梯形的高就是平行四边形的高，所以，梯形的面积=（上底+下底）×高÷2。

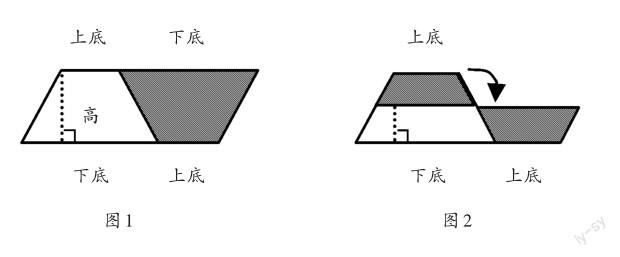
2.把梯形割补成其他学过的图形。

把梯形的上底和下底对折，中间出現一条折痕（中位线），然后沿折痕剪开，拼成一个平行四边形（如图2）。这个平行四边形的高就是梯形的高的一半，上底加下底就是平行四边形的底。因为梯形的面积=平行四边形的面积，所以，梯形的面积=（上底+下底）×高÷2。